Abstract
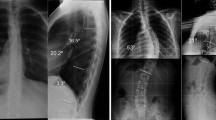
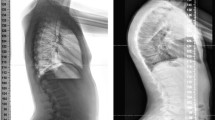
Deformity in adolescent thoracic spine has high prevalence worldwide. The objective of this work was to study the biomechanical behavior on the thoracic spines of adolescents under asymmetric ligament load in kyphosis and rectified kyphosis. Two finite element models of an adolescent thoracic segment, T5–T10, were generated with every bone component, intervertebral discs, the flavum, intertransverse and supraspinous ligaments. The three-dimensional geometry of the T5-T10 was generated with Autodesk®Maya®, and HyperMesh® version 14.0 was used to generate the finite element models. Asymmetric ligament load of 10 N was applied in the T8–T9, with and without axial load of 400 N in the T5 vertebra. Rectified kyphosis showed the highest rotational displacement of the T8–T9 unit: 0.16° with axial load and asymmetric ligament load, and 0.22° with asymmetric ligament load alone. Kyphosis exhibited rotational displacement of 0.11° and 0.12°, respectively, for the same load conditions. Rectified kyphosis subjected to an asymmetric ligament force showed greater inoperability of the facet joints, and therefore greater vulnerability to vertebral rotation. The results suggest the need for greater attention to the vertebral assessments in the sagittal plane, beginning from the growth spurt period, to adopt preventive therapeutic in vertebral deformities such as adolescent idiopathic scoliosis.






Similar content being viewed by others

References
Ali A, Hosseini M, Sahari BB (2010) A review and comparison on some rubber elasticity models. J Sci Ind Res 69:495–500
Cahill PJ, Wang W, Asghar J, Booker R, Betz RR, Ramsey C, Baran G (2012) The use of a transition rod may prevent proximal junctional kyphosis in the thoracic spine following scoliosis surgery: a finite element analysis. Spine 37(12):E687–E695
Castelein RM, Van Dieen JH, Smit TH (2005) The role of dorsal shear forces in the pathogenesis of adolescent idiopathic scoliosis—a hypothesis. Med Hypotheses 65:501–508
Cheng FH, Shih SL, Chou WK, Liu CL, Sung WH, Chen CS (2010) Finite element analysis of the scoliosis spine under different loading conditions. Bio-Med Mater Eng 20(5):251–259
Clément JL, Geoffray A, Yagoubi F, Edouard C, Solla F, Oborocianu I, Rampal V (2013) Relationship between thoracic hypokyphosis, lumbar lordosis and sagittal pelvic parameters in adolescent idiopathic scoliosis. Eur Spine J 22:2414–2420
Dickson RA, Lawton JO, Archer IA, Butt WP (1984) The pathogenesis of idiopathic scoliosis: biplanar spinal asymmetry. J Bone Joint Surg 66(1):8–15
Dong L, Li G, Mao H, Marek S, Yang KH (2013) Development and validation of a 10-year-old child ligamentous cervical spine finite element model. Ann Biomed Eng 41(12):2538–2552
El Masri F, Sapin de Brosses E, Rhissassi K, Skalli W, Mitton D (2012) Apparent young’s modulus of vertebral cortico-cancellous bone specimens. Comput Methods Biomech Biomed Eng 15(1):23–28
Fok J, Adeeb S, Carey J (2010) FEM simulation of non-progressive growth from asymmetric loading and vicious cycle theory: scoliosis study proof of concept. Open Biomed Eng J 4:162–169
Ghista DN, Vivian GR, Subbaraj K, Lozada PJ, Srinivasan TM, Barnes G (1988) Biomechanical basis of optimal scoliosis surgical-correction. J Biomech 21(2):77–88
Greco M, Rocha da Costa LJ (2012) Discussion on The logarithmic strain measure applied to the nonlinear positional formulation for space truss analysis [Finite Element in Analysis and Design 45 (2009) 632 639] and Nonlinear positional formulation for space truss analysis [Finite Element in Analysis and Design 42 (2006) 1079 1086]. Finite Elem Anal Des 52(1):93–95
Janssen MM, Drevelle X, Humbert L, Skalli W, Castelein RM (2009) Differences in male and female spino-pelvic alignment in asymptomatic young adults: a three-dimensional analysis using upright low-dose digital biplanar X-rays. Spine 34(23):E826–E832
Janssen MM, Vincken KL, Kemp B, Obradov M, De Kleuver M, Viergever MA et al (2010) Pre-existent vertebral rotation in the human spine is influenced by body position. Stud Health Technol Inform 19:1728–1734
Jaramillo HE, Gomez L, Garcia JJ (2015) A finite element model of the L4-L5-S1 human spine segment including the heterogeneity and anisotropy of the discs. Acta Bioeng Biomech 17(2):15–24
Karasudhi P (1991) Foundations of solid mechanics, 1st edn. Kluwer, Waterloo, pp 98–102
Kotwicki T (2008) Intravertebral deformation in idiopathic scoliosis—a transverse plane computer tomographic study. J Pediatr Orthop 28:225–229
Kouwenhoven JWM, Smit TH, Van Der Veen AJ, Kingma I, Castelein RM (2007) Effects of dorsal versus ventral shear loads on the rotational stability of the thoracic spine. Spine 32:2545–2550
Kuo CS, Hu HT, Lin RM, Huang KY, Lin PC, Zhong ZC et al (2010) Biomechanical analysis of the lumbar spine on facet joint force and intradiscal pressure: a finite element study. BMC Musculoskelet Disord 11:151–164
Kurutz M (2010) Finite element modelling of human lumbar spine. In: Moratal D (ed) Finite element analysis. InTech, pp 209–236. ISBN: 978-953-307-123-7
Lan CC, Kuo CS, Chen CH, Hu HT (2013) Finite element analysis of biomechanical behavior of whole thoracic-lumbar spine with ligamentous effect. Changhua J Med 11:26–41
Little JP, Adam C (2011) Patient-specific computational biomechanics for simulating adolescent scoliosis surgery: predicted vs clinical correction for a preliminary series of six patients. Int J Numer Methods Biomed Eng 27:347–356
Lu YM, Hutton WC, Gharpuray VM (1996) Can variation in Intervertebral disc height affect the mechanical function of the disc? Spine 21:2208–2217
Meijer GJM (2011) Development of a non-fusion scoliosis correction device numerical modelling of scoliosis correction, Ph.D. Thesis—College voor Promoties, Universiteit Twente, 165f. Enschede, The Netherlands
Meijer GJM, Homminga J, Hekman EEG, Veldhuizen AG, Verkerke GJ (2010) The effect of three-dimensional geometrical changes during adolescent growth on the biomechanics of a spinal motion segment. J Biomech 43(8):1590–1597
Nault ML, Thiong JMM, Roy-Beaudry M, Turgeon I, De Guise J, Labelle H et al (2014) Three-dimensional spinal morphology can differentiate between progressive an nonprogressive patients with adolescent idiopathic scoliosis at the initial presentation. Spine Deformity 39(10):E601–E606
Pal GP (1991) Mechanism of production of scoliosis: a hypothesis. Spine 16:288–292
Panjabi MM, Brand RA, White AA (1976) Mechanical properties of the human thoracic spine. J Bone Joint Surg 58-A:642–652
Panjabi MM, Takata K, Goel V (1991) Thoracic human vertebrae-quantitative three-dimensional anatomy. Spine 16:889–901
Ran B, Zhang GY, Shen F, Chen JY, Wu JB, Zhao FC et al (2014) Comparison of the sagittal profiles among thoracic idiopathic scoliosis patients with different Cobb angles and growth potentials. J Orthop Surg Res 9:19
Rohlmann A, Zander T, Bergmann G (2006) Spinal loads after osteoporotic vertebral fractures treated by vertebroplasty or kyphoplasty. Eur Spine J 15:1255–1264
Roussouly P, Labelle H, Rouissi J, Bodin A (2013) Pre- and post-operative sagittal balance in idiopathic scoliosis: a comparison over the ages of two cohorts of 132 adolescents and 52 adults. Eur Spine J 22(2):S203–S215
Schlosser TP, Shah SA, Reichard SJ, Roger K, Vincken KL, Castelein RM (2014) Differences in early sagittal plane alignment between thoracic and lumbar adolescent idiopathic scoliosis. Spine J 2(14):282–290
Schmidt H, Heuer F, Wilke HJ (2009) Which axial and bending stiffnesses of posterior implants are required to design a flexible lumbar stabilization system? J Biomech 42:48–54
Sevastik J, Aaro S, Normelli H (1984) Scoliosis: experimental and clinical studies. Clin Orthop Relat Res 191:27–34
Stokes IAF, Burwell RG, Dangerfield PH (2006) Biomechanical spinal growth modulation and progressive adolescent scoliosis: a test of the “vicious cycle” pathogenetic hypothesis: summary of an electronic focus group debate of the IBSE. Scoliosis 1:16
Stokes IA, Gardner-Morse M (1991) Analysis of the interaction between vertebral lateral deviation and axial rotation in scoliosis. J Biomech 24(8):753–759
Tyndyk MA, Barron V, Mchugh PE, O’Mahoney D (2007) Generation of a finite element model of the thoracolumbar spine. Acta Bioeng Biomech 9:35–46
Van Der Plaats A, Veldhuizen AG, Verkerke GJ (2007) Numerical simulation of asymmetrically altered growth as initiation mechanism of scoliosis. Ann Biomed Eng 35:1206–1215
Villemure I, Aubin CE, Dansereau J, Labelle H (2002) Simulation of progressive deformities in adolescent idiopathic scoliosis using a biomechanical model integrating vertebral growth modulation. J Biomech Eng 124:784–790
Wang W, Baran GR, Betz RR, Samdani AF, Pahys JM, Cahill PJ (2014) The use of finite element models to assist understanding and treatment for scoliosis: a review paper. Spine Deformity 2:10–27
White AA (1971) Kinematics of the normal spine as related to scoliosis. J Biomech 4:405–411
Willner S, Johnson B (1983) Thoracic kyphosis and lumbar lordosis during the growth period in children. Acta Paediatr Scand 72(6):873–878
Zander T, Rohlmann A, Calisse J, Bergmann G (2001) Estimation of muscle forces in the lumbar spine during upper body inclination. Clin Biomech 16:73–80
Acknowledgements
The authors would like to acknowledge CNPq (National Council of Scientific and Technological Development) and FAPEMIG (Minas Gerais State Research Foundation), in Brazil, for their financial support under grant numbers 441573/2014-2, 302376/2016-0 and TEC-PPM-00409-16, respectively. The authors would also like to acknowledge the grammar revision service provided by the Pró-Reitoria de Pesquisa da Universidade Federal de Minas Gerais.
Author information
Authors and Affiliations
Corresponding author
Additional information
Technical Editor: Sadek C. Absi Alfaro.
Rights and permissions
About this article
Cite this article
Aroeira, R.M.C., Pertence, A.E.M., Kemmoku, D.T. et al. The effect of hypokyphosis on the biomechanical behavior of the adolescent thoracic spine. J Braz. Soc. Mech. Sci. Eng. 40, 128 (2018). https://doi.org/10.1007/s40430-018-1061-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40430-018-1061-4