Skip to main content
SpringerLink
Log in

Turbulent channel flow perturbed by triangular ripples

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

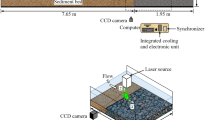
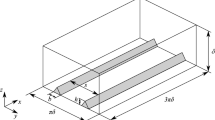
This paper presents an experimental investigation of the perturbation of a turbulent closed-conduit flow by two-dimensional triangular ripples. Two ripple configurations were employed: one single asymmetric triangular ripple, and two consecutive asymmetric triangular ripples, all of them with the same geometry. Different water flows were imposed over either one or two ripples fixed to the bottom wall of a closed conduit, and the flow field was measured by particle image velocimetry (PIV). Reynolds numbers based on the channel height were moderate, varying between 27500 and 34700. The regime was hydraulically smooth, and the blockage ratio was significant. Experimental data for this specific case remain scarce, and the physics involved has yet to be fully elucidated. Using the instantaneous flow fields, the mean velocities and fluctuations were computed, and the shear stresses over the ripples were determined. The velocities and stresses obtained in this way for the single ripple and for the pair of ripples are compared, and the surface shear stress is discussed in terms of bed stability. Our results show that for the single and upstream ripples, the shear stress increases at the leading edge and decreases toward the crest, while for the downstream ripple it decreases monotonically between the reattachment point and the crest. The stress distribution over the downstream ripple, which is different from both the upstream and single ripples, is shown to sustain existing ripples over loose beds.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Abbreviations

A :

Constant

B :

Constant

d :

Diameter (m)

f :

Darcy friction factor

h :

Local height of the ripple (m)

H :

Channel height (m)

\(H_\text{ eff }\) :

Distance between the PVC plates and the top wall of the channel (m)

i :

Imaginary number

k :

Wave number (m\(^{-1}\))

L :

Ripple length (m)

\(l_v\) :

Viscous length (m)

P :

Turbulence production term (m\(^2\)/s\(^3\))

\(P_{\text {max}}\) :

Maximum value of turbulence production (m\(^2\)/s\(^3\))

Q :

Volumetric flow rate (m\(^3\)/h)

Re :

Reynolds number based on the channel height

\(Re_{\text {dh}}\) :

Reynolds number based on the hydraulic diameter

t :

Time (s)

u :

Longitudinal component of the velocity (m/s)

\(\overline{U}\) :

Cross-sectional mean velocity (m/s)

\(U_0\) :

Velocity at the channel centerline (m/s)

\(u_*\) :

Shear velocity (m/s)

v :

Vertical component of the velocity (m/s)

\(\mathbf {V}\) :

Velocity vector (m/s)

x :

Horizontal coordinate (m)

y :

Vertical coordinate (m)

\(\Delta\) :

Perturbation field

\(\kappa\) :

von Kármán constant

\(\lambda\) :

Wavelength (m)

\(\mu\) :

Dynamic viscosity (Pa s)

\(\nu\) :

Kinematic viscosity (m\(^2\)/s)

\(\rho\) :

Density (kg/m\(^3\))

\(\tau\) :

Shear stress (N/m\(^2\))

\(\theta\) :

Angle between the horizontal and the ripple surface (\(^o\))

0:

Relative to the flat surface (unperturbed flow)

bla:

Relative to Blasius correlation

d :

Relative to the displaced coordinate system

dh:

Relative to the hydraulic diameter

k :

Relative to Fourier space

max:

Maximum value

v :

Relative to the viscous layer

\(\theta\) :

Aligned with the ripple surface

\(+\) :

Normalized by the viscous length \(l_v\) or by the shear velocity \(u_{*,0}\)

\(\overline{\quad }\) :

Averaged in time

\('\) :

Fluctuation

\(\hat{\quad }\) :

Perturbation

References

  1. Jackson PS, Hunt JCR (1975) Turbulent wind flow over a low hill. Quart J R Meteorol Soc 101:929–955

    Article  Google Scholar 

  2. Hunt JCR, Leibovich S, Richards KJ (1988) Turbulent shear flows over low hills. Quart J R Meteorol Soc 114:1435–1470

    Article  Google Scholar 

  3. Belcher SE, Hunt JCR (1998) Turbulent flow over hills and waves. Ann Rev Fluid Mech 30:507–538

    Article  MathSciNet  Google Scholar 

  4. Poggi D, Katul G, Albertson J, Ridolfi L (2007) An experimental investigation of turbulent flows over a hilly surface. Phys Fluids 19(3):036601

    Article  MATH  Google Scholar 

  5. Carruthers DJ, Hunt JCR (1990) Fluid mechanics of airflows over hills: turbulence, fluxes, and waves in the boundary layer. Atmospheric processes over complex terrain, vol 23. American Meteorological Society, Boston, pp 83–108

    Chapter  Google Scholar 

  6. Weng MS, Hunt JCR, Carruthers DJ, Warren A, Wiggs GFS, Livingstone I, Castro I (1991) Air flow and sand transport over sand-dunes. Acta Mech 1–21

  7. Kroy K, Sauermann G, Herrmann HJ (2002) Minimal model for aeolian sand dunes. Phys Rev E 66:031302

    Article  Google Scholar 

  8. Kroy K, Sauermann G, Herrmann HJ (2002) Minimal model for sand dunes. Phys Rev Lett 88:054301

    Article  Google Scholar 

  9. Andreotti B, Claudin P, Douady S (2002) Selection of dune shapes and velocities. Part 1: dynamics of sand, wind and barchans. Eur Phys J B 28:321–329

    Article  Google Scholar 

  10. Andreotti B, Claudin P, Douady S (2002) Selection of dune shapes and velocities. Part 2: a two-dimensional model. Eur Phys J B 28:341–352

    Article  Google Scholar 

  11. Howard AD, Morton JB, Gad-El Hak M, Pierce DB (1978) Sand transport model of barchan dune equilibrium. Sedimentology 25(3):307–338

    Article  Google Scholar 

  12. Wiggs GFS, Livingstone A, Warren A (1996) The role of streamline curvature in sand dune dynamics: evidence from field and wind tunnel measurements. Geomorphology 17:29–46

    Article  Google Scholar 

  13. Sauermann G (2001) Modeling of wind blown sand and desert dunes. Ph.D. thesis Modeling of wind blown sand and desert dunes. Universität Stuttgart

  14. Sauermann G, Andrade JS, Maia LP, Costa UMS, Araújo AD, Herrmann HJ (2003) Wind velocity and sand transport on a barchan dune. Geomorphology 54:245–255

    Article  Google Scholar 

  15. Marquillie M, Laval JP, Dolganov R (2008) Direct numerical simulation of a separated channel flow with a smooth profile. J Turbul 9:N1

    Article  Google Scholar 

  16. Marquillie M, Ehrenstein U, Laval JP (2011) Instability of streaks in wall turbulence with adverse pressure gradient. J Fluid Mech 681:205–240

    Article  MATH  Google Scholar 

  17. Franklin EM, Charru F (2011) Subaqueous barchan dunes in turbulent shear flow. Part 1: Dune motion. J Fluid Mech 675:199–222

    Article  MATH  Google Scholar 

  18. Charru F, Franklin EM (2012) Subaqueous barchan dunes in turbulent shear flow. Part 2: fluid flow. J Fluid Mech 694:131–154

    Article  MATH  Google Scholar 

  19. Franklin EM, Ayek GA (2013) The perturbation of a turbulent boundary layer by a two-dimensional hill. J Braz Soc Mech Sci 35:337–346

    Article  Google Scholar 

  20. Walker IJ, Nickling WG (2003) Simulation and measurement of surface shear stress over isolated and closely spaced transverse dunes in a wind tunnel. Earth Surf Process Landforms 28:1111–1124

    Article  Google Scholar 

  21. Florez JEC, Franklin EM (2016) The formation and migration of sand ripples in closed conduits: experiments with turbulent water flows. Exp Therm Fluid Sci 71:95–102

    Article  Google Scholar 

  22. Coleman SE, Nikora VI, McLean SR, Clunie TM, Schlicke T, Schlicke BW (2006) Equilibrium hydrodynamics concept for developing dunes. Phys Fluids 18:105104

    Article  Google Scholar 

  23. Mendez MA, Raiola M, Masullo A, Discetti S, Ianiro A, Theunissen R, Buchlin JM (2017) POD-based background removal for particle image velocimetry. Exp Therm Fluid Sci 80:181–192

    Article  Google Scholar 

  24. Franklin EM (2015) Formation of sand ripples under a turbulent liquid flow. Appl.Math Model 39(23):7390–7400

    Article  MathSciNet  Google Scholar 

  25. Schlichting H (2000) Boundary-layer theory. Springer

  26. Engelund F, Fredsoe J (1982) Sediment ripples and dunes. Ann Rev Fluid Mech 14:13–37

    Article  MATH  Google Scholar 

  27. Charru F (2006) Selection of the ripple length on a granular bed sheared by a liquid flow. Phys Fluids 18:121508

    Article  MATH  Google Scholar 

Download references

Acknowledgements

Fernando David Cúñez Benalcázar is grateful to SENESCYT (Programa de Becas Convocatoria Abierta 2014 Segunda Fase) and to FAPESP (grant no. 2016/18189-0), and Gabriel Victor Gomes de Oliveira is grateful to FAPESP (grant no. 2015/15001-8) and to CAPES for providing financial support. Erick de Moraes Franklin would like to express his gratitude to FAPESP (grant nos. 2012/19562-6 and 2016/13474-9) and CNPq (grant no. 400284/2016-2) for the financial support they provided.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, University of Campinas-UNICAMP, Campinas, Brazil

    Fernando David Cúñez, Gabriel Victor Gomes de Oliveira & Erick de Moraes Franklin

Authors
  1. Fernando David Cúñez
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gabriel Victor Gomes de Oliveira
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Erick de Moraes Franklin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Erick de Moraes Franklin.

Additional information

Technical Editor: Jader Barbosa Jr.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cúñez, F.D., Gomes de Oliveira, G.V. & de Moraes Franklin, E. Turbulent channel flow perturbed by triangular ripples. J Braz. Soc. Mech. Sci. Eng. 40, 138 (2018). https://doi.org/10.1007/s40430-018-1050-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1050-7

Keywords

Search

Navigation