Skip to main content
SpringerLink
Log in

Analytical study on motion and shape of creeping Boger drops falling through viscoelastic media

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

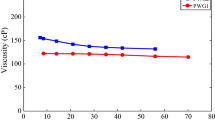
Abstract

In the present study, an analytical solution based on a double perturbation method is obtained to simulate the creeping motion of a Boger drop descending in an immiscible viscoelastic quiescent medium. The perturbation parameters are considered to be the Deborah number defined based on the relaxation times of interior and exterior media and the Capillary number. The Oldroyd-B model is implemented as a constitutive equation for both interior and exterior phases. The analytical solutions are obtained up to second order of perturbation expansion for both phases. The motion of the droplet in the surrounding medium is considered to be creeping. Effects of different parameters including, Deborah numbers, viscosity ratios, elasto-capillary number, and viscosity ratio between the drop and external flows are investigated on the shape, motion, and stream function in detail. In contrast to the generally spherical shape of creeping drops in Newtonian regimes, it is shown that the effect of elasticity in a non-Newtonian scenario can feature prolate or oblate shapes. It is shown that an increment in elastic properties of interior fluid is followed by decrement in the terminal velocity of the droplet, while an increment in elasticity of exterior fluid has a contrary effect and increases the terminal velocity. The results have shown suitable agreements with previously reported experimental results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Hadamard J (1911) Mouvement permanent lent d’une sphere liquide et visqueuse dans un liquide. C R Acad Sci Paris 152:1735–1738

    MATH  Google Scholar 

  2. Rybczynski W (1911) Bull. Uber die fortschreitende Bewegung einer flüssigen Kugel in einem zähen Medium. Bull Acad Sci Crac 1:40–46

    Google Scholar 

  3. Taylor TD, Acrivos A (1964) On the deformation and drag of a falling viscous drop at low Reynolds number. J Fluid Mech 18:466–476

    Article  MathSciNet  MATH  Google Scholar 

  4. Taylor GI (1934) The formation of emulsions in definable fields of flow. Proc R Soc Lond A 146:501–523

    Article  Google Scholar 

  5. Stone HA (1994) Dynamics of drop deformation and breakup in viscous fluids. Annu Rev Fluid Mech 26:65–102

    Article  MathSciNet  MATH  Google Scholar 

  6. Koh CJ, Leal LG (1989) The stability of drop shapes for translation at zero Reynolds number through a quiescent fluid. Phys Fluids A 1(8):1309–1313

    Article  Google Scholar 

  7. Smolianski A, Haario A, Luukka P (2003) Numerical bubble dynamics. Comput Aided Chem Eng 14:941–946

    Article  MATH  Google Scholar 

  8. Sostarecz MC, Belmonte A (2003) Motion and shape of a viscoelastic drop falling through a viscose fluid. J Fluid Mech 497:235–252

    Article  MATH  Google Scholar 

  9. Pozrikidis C (1997) Numerical studies of singularity formation at free surface and fluid interface in two dimensional stokes flow. J Fluid Mech 331:145–167

    Article  MathSciNet  MATH  Google Scholar 

  10. Joseph DD, Nelson J, Renardy M, Renardy Y (1991) Two dimensional cusped interfaces. J Fluid Mech 223:383–409

    Article  Google Scholar 

  11. Joseph DD (1992) Understanding cusped interfaces. J Non Newton Fluid Mech 44:127–148

    Article  MATH  Google Scholar 

  12. Liu YJ, Liao TY, Joseph DD (1995) A two-dimensional cusp at the trailing edge of an air bubble rising in a viscoelastic liquid. J Fluid Mech 304:321–342

    Article  Google Scholar 

  13. Coutanceeau M, Hajjann M (1982) Viscoelastic effect on the behaviour of an air bubble rising axially in a tube. Mech Phys Bubbles Liq 38:199–207

    Article  Google Scholar 

  14. Zana E, Leal LG (1978) The dynamics and dissolution of gas bubbles in a viscoelastic fluid. Int J Multiph Flow 4:237–262

    Article  Google Scholar 

  15. Noh DS, Kang IS, Leal LG (1993) Numerical solutions for the deformation of a bubble rising in dilute polymeric fluids. Phys Fluids 5(6):1315–1332

    Article  MATH  Google Scholar 

  16. Hinch EJ, Acrivos A (1980) Long slender drops in a simple shear flow. J Fluid Mech 98:305–328

    Article  MathSciNet  MATH  Google Scholar 

  17. Hinch EJ (1980) The evolution of slender inviscid drops in an axisymmetric straining flow. J Fluid Mech 101:545–553

    Article  MathSciNet  MATH  Google Scholar 

  18. Sherwood JD (1981) Spindle-shaped drops in a viscous extensional flow. Math Proc Camb Phil Soc 90:529–536

    Article  MathSciNet  MATH  Google Scholar 

  19. Khakhar DV, Ottino JM (1986) Deformation and breakup of slender drops in linear flows. J Fluid Mech 166:265–285

    Article  MATH  Google Scholar 

  20. Bentley BJ, Leal LG (1986) An experimental investigation of drop deformation and breakup in steady, two-dimensional linear flows. J Fluid Mech 167:241–283

    Article  MATH  Google Scholar 

  21. Mukherjee S, Sarkar K (2011) Viscoelastic drop falling through a viscous medium. Phys Fluids 23(1):013101

    Article  Google Scholar 

  22. Kishore N, Chhabra RP, Eswaran V (2008) Effect of dispersed phase rheology on the drag of single and of ensembles of fluid spheres at moderate Reynolds numbers. Chem Eng J 141:387–392

    Article  Google Scholar 

  23. You R, Borhan A, Haj-Hariri H (2008) A finite volume formulation for simulating drop motion in a viscoelastic two-phase system in a viscoelastic two-phase system. J Non Newton Fluid Mech 153:109–129

    Article  MATH  Google Scholar 

  24. Acharya A, Mashelkar RA (1978) Motion of liquid drops in rheologically complex fluids. Can J Chem Eng 56(1):19–25

    Article  Google Scholar 

  25. Acharya A, Mashelkar RA, Ulbrecht J (1978) Mechanics of bubble motion and deformation in non-newtonian media. Chem Eng Sci 32(8):863–872

    Article  Google Scholar 

  26. Mohan V, Nagarajan R, Venkateswarlu D (1972) Fall of drops in non-Newtonian media. Can J Chem Eng 50:37

    Article  Google Scholar 

  27. Wagner MG, Slattery JC (1971) Slow flow of a non-Newtonian fluids past a droplet. AIChE J 17:1198–1207

    Article  Google Scholar 

  28. Dairenieh LS, McHugh AJ (1985) Viscoelastic fluid flow past a submerged spheroidal body. J Non Newton Fluid Mech 19:81–111

    Article  MATH  Google Scholar 

  29. Batchelor GK (1967) An introduction to fluid dynamics. Cambridge University, Cambridge

    MATH  Google Scholar 

  30. Vamerzani BZ, Norouzi M, Firoozabadi B (2014) Analytical solution for creeping motion of a viscoelastic drop falling through a Newtonian fluid. Korea Aust Rheol J 26(1):91–104

    Article  Google Scholar 

  31. Vamerzani BZ, Norouzi M, Firoozabadi B (2016) Theoretical and experimental study on the motion and shape of viscoelastic falling drops through Newtonian media. Rheol Acta 55(11–12):935–955

    Article  Google Scholar 

  32. Bird RB, Armstrong RC, Hassager O (1987) Dynamics of polymeric liquids, fluid dynamics, vol 1, 2nd edn. Wiley, New York

    Google Scholar 

  33. White FM (2006) Viscose fluid flow, 3rd edn. McGraw-Hill, New York

    Google Scholar 

  34. Landau L, Lifshitz I (1959) Fluid mechanics. Pergamon, Oxford

    MATH  Google Scholar 

  35. Joseph DD, Beavers GS (1972) The free surface on a liquid between cylinders rotating at different speeds speeds. Part 1 Arch Ration Mech Anal 49:321–380

    Article  MathSciNet  Google Scholar 

  36. Mckinley GH (2005) Dimensionless groups for understanding free surface flows of complex fluids. Sco Rheol Bull 74(2):6–9

    Google Scholar 

  37. Wanchoo RK, Sharma SK, Ritu Gupta (2003) Shape of a Newtonian liquid drop moving through an immiscible quiescent non-Newtonian liquid. Chem Eng Process 42:387–393

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to express their gratitude to Professor Morton Denn of the Levich Institute, City College of New York, USA, for his valuable discussions and guidance during the present research.

Author information

Authors and Affiliations

  1. Mechanical Engineering Department, Shahrood University of Technology, Shahrood, Iran

    M. Norouzi

  2. School of Engineering, University of Liverpool, Brownlow Hill, Liverpool, L69 3GH, UK

    M. Davoodi

Authors
  1. M. Norouzi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Davoodi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Norouzi.

Additional information

Technical Editor: Cezar Negrao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Norouzi, M., Davoodi, M. Analytical study on motion and shape of creeping Boger drops falling through viscoelastic media. J Braz. Soc. Mech. Sci. Eng. 40, 125 (2018). https://doi.org/10.1007/s40430-018-1046-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1046-3

Keywords

Search

Navigation