Skip to main content
SpringerLink
Log in

MHD free convective heat transfer in a Walter’s liquid-B fluid past a convectively heated stretching sheet with partial wall slip

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

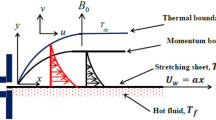
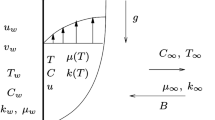
The prime aim of the present investigation is to capture the mechanism of Navier’s velocity slip and convective thermal boundary condition on the flow of MHD viscoelastic fluid over a stretching surface. Additionally, the analysis also includes the effect of natural convection and thermal radiation. The governing boundary layer equations are transformed into a set of highly non-linear ordinary differential equations using suitable similarity transforms. Galerkin Finite element method is used to solve this boundary value problem. Effects of pertinent flow parameters on the Skin friction coefficient, Nusselt number, velocity and temperature, are described graphically. Numerical results obtained in this paper are compared with earlier published results and are found to be in excellent agreement. Significant findings of the present article are the conjugate effect of partial velocity slip and viscoelasticity of the fluid on Skin friction, Nusselt number, velocity and temperature. The analysis shows that presence of partial velocity slip changes the behavior of Nusselt number and skin friction coefficients significantly in comparison to the no slip condition. The present problem has potential to serve as a model for many industrial processes such as cooling and/or drying of paper and textile, rolling sheet drawn from a die, manufacturing of polymeric sheets, sheet glass and crystalline materials, etc.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Abbreviations

\(a\) :

Constant parameter (s−1)

\(A\) :

Rate of strain tensor (s−1)

\(b\) :

\(= \left( {b_{x} ,b_{y} ,0} \right)\) body force vector (N)

\(B\) :

Magnetic field (Kg s−2 A−1)

\({\text{Bi}}\) :

Biot number

\({\text{Cf}}_{x}\) :

Local skin friction coefficient

\(f\) :

Dimensionless stream function

\(g\) :

Gravitational acceleration (ms−2)

\(Gr_{x}\) :

Grashof number

\(h\) :

Element size (m)

\(I\) :

Unit tensor

\(k\) :

Thermal conductivity (Wm−1 K−1)

\(k^{*}\) :

Rosseland mean absorption coefficient (m−1)

\(k_{0}\) :

First order coefficient of short relaxation (kg m−1)

\(M\) :

Magnetic parameter

\(N\) :

Velocity slip factor (m)

\(p\) :

Pressure (Pa)

\(Nu_{x}\) :

Local Nusselt number

\(\Pr\) :

Prandtl number

\(\Pr_{\text{eff}}\) :

Effective Prandtl number

\(q_{r}\) :

Radiative heat flux (Wm−2)

\(q_{s}\) :

Wall heat flux (Wm−2)

\(R\) :

Radiation parameter

\(\text{Re}_{x}\) :

Local Reynolds number

\(T\) :

Temperature (K)

\(T_{s}\) :

Temperature of the left side of surface (K)

\(T_{\infty }\) :

Temperature in free stream (K)

\(t\) :

Time (s)

\(V\) :

\(= \left( {u,v,0} \right)\) velocity vector (ms−1)

\(u_{s}\) :

Stretching sheet velocity (ms−1)

\(u_{\text{slip}}\) :

Slip velocity (ms−1)

\(\alpha\) :

Viscoelasticity parameter

\(\alpha_{m}\) :

Thermal diffusivity (m2 s−1)

\(\beta\) :

Thermal expansion coefficient (K−1)

\(\gamma\) :

Velocity slip parameter

\(\varUpsilon\) :

Cauchy stress tensor (Pa)

\(\sigma\) :

Electrical conductivity (Sm−1)

\(\rho\) :

Density (kg m−3)

\(\lambda\) :

Thermal buoyancy parameter

\(\left( {\rho C_{p} } \right)\) :

Specific heat capacity of the fluid (JK−1)

\(\theta\) :

Dimensionless temperature

\(\upsilon\) :

Kinematic coefficient of viscosity (m2 s−1)

\(\psi\) :

Stream function (m2 s)

\(\eta\) :

Similarity variable

\(\mu\) :

Dynamic viscosity (kg m−1 s−1)

\(\sigma^{*}\) :

Stefan Boltzmann constant (Wm−2 K−4)

\(\tau_{s}\) :

Wall shear stress (kg m−1 s−2)

References

  1. Sakiadis BC (1961) Boundary layer behavior on continuous solid surface: II –Boundary layer on a continuous flat surface. AIChE J 7:221–225

    Article  Google Scholar 

  2. Crane LJ (1970) Flow past a stretching plate. J Appl Math Phys (ZAMP) 21:645–647

    Article  Google Scholar 

  3. Vajravelu K (2001) Viscous flow over a nonlinearly stretching sheet. Appl Math Comput 124(3):281–288

    MathSciNet  MATH  Google Scholar 

  4. Seth GS, Sharma R, Kumbhakar B, Chamkha AJ (2016) Hydromagnetic flow of heat absorbing and radiating fluid over exponentially stretching sheet with partial slip and viscous and Joule dissipation. Eng. Comput 33(3):907–925

    Article  Google Scholar 

  5. Majeed A, Zeeshan A, Ellahi R (2016) Unsteady ferromagnetic liquid flow and heat transfer analysis over a stretching sheet with the effect of dipole and prescribed heat flux. J Mol Liq 223:528–533

    Article  Google Scholar 

  6. Ellahi R, Tariq MH, Hassan M, Vafai K (2017) On boundary layer nano-ferroliquid flow under the influence of low oscillating stretchable rotating disk. J Mol Liq 229:339–345

    Article  Google Scholar 

  7. Andersson HI, Bech KH, Dandapat BS (1992) Magnetohydrodynamic flow of a power law fluid over a stretching sheet. Int J Nonlinear Mech 72:929–936

    Article  MATH  Google Scholar 

  8. Mukhopadhyay S (2013) Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin Phys B 22(7):074701

    Article  Google Scholar 

  9. Rajagopal KR, Bhatnagar RK (1995) Exact solutions for some simple flows of an Oldroyd-B fluid. Acta Mech 113(1–4):233–239

    Article  MathSciNet  MATH  Google Scholar 

  10. Beard DW, Walters K (1964) Elastico-viscous boundary-layer flows I. Two-dimensional flow near a stagnation point. Math Proc Cambridge Philos Soc 60:667–674

    Article  MathSciNet  MATH  Google Scholar 

  11. Khan AA, Usman H, Vafai K, Elahi R (2016) Study of peristaltic flow of magnetohydrodynamic Walter’s B fluid with slip and heat transfer. Sci Iran 23(6):2650–2662

    Google Scholar 

  12. Bhatti MM, Zeeshan A, Ellahi R (2016) Endoscope analysis on peristaltic blood flow of Sisko fluid with Titanium magneto-nanoparticles. Comput Biol Med 78:29–41

    Article  Google Scholar 

  13. Bhatti MM, Ellahi R, Zeeshan A (2016) Study of variable magnetic field on the peristaltic flow of Jeffrey fluid in a non-uniform rectangular duct having compliant walls. J Mol Liq 222:101–108

    Article  Google Scholar 

  14. Ellahi R, Shivanian E, Abbasbandy S, Hayat T (2016) Numerical study of magnetohydrodynamics generalized Couette flow of Eyring-Powell fluid with heat transfer and slip condition. Int J Numer Method H 26(5):1433–1445

    Article  MathSciNet  MATH  Google Scholar 

  15. Pavlov KB (1974) Magnetohydrodynamic flow of an incompressible viscous fluid caused by deformation of a plane surface. Magnitnaya Gidrodinamika 4:146–147

    Google Scholar 

  16. Andersson VPH (1992) MHD flow of a viscoelastic fluid past a stretching surface. Acta Mech 95(1–4):227–230

    Article  MathSciNet  MATH  Google Scholar 

  17. Liu IC (2005) Flow and heat transfer of an electrically conducting fluid of second grade in a porous medium over a stretching sheet subject to a transverse magnetic field. Int J Nonlinear Mech 40(4):465–474

    Article  MATH  Google Scholar 

  18. Khan AA, Ellahi Muhammad S, Zia QZ (2016) Bionic study of variable viscosity on MHD peristaltic flow of Pseudoplastic fluid in an asymmetric channel. J Magn 21(2):273–280

    Article  Google Scholar 

  19. Bhatti MM, Zeeshan A, Ellahi R (2017) Simultaneous effects of coagulation and variable magnetic field on peristaltically induced motion of Jeffrey nanofluid containing gyrotactic microorganism. Microvasc Res 110:32–42

    Article  Google Scholar 

  20. Bhatti MM, Zeeshan A, Ellahi R, Ijaz N (2017) Heat and mass transfer of two-phase flow with Electric double layer effects induced due to peristaltic propulsion in the presence of transverse magnetic field. J Mol Liq 230:237–246

    Article  Google Scholar 

  21. Sheikholeslami M, Zia QM, Ellahi R (2016) Influence of induced magnetic field on free convection of nanofluid considering Koo-Kleinstreuer-Li (KKL) correlation. Appl Sci 6(11):324

    Article  Google Scholar 

  22. Bhatti MM, Zeeshan A, Ijaz N, Ellahi R (2017) Heat transfer and inclined magnetic field analysis on peristaltically induced motion of small particles. J Braz Soc Mech Sci Eng. https://doi.org/10.1007/s40430-017-0760-6

    Google Scholar 

  23. Howell John R, Menguc MP, Siegel R (2010) Thermal radiation heat transfer. CRC press Taylor and Francis Group, New York

    Google Scholar 

  24. Chien-Hsin Chen (2010) On the analytic solution of MHD flow and heat transfer for two types of viscoelastic fluid over a stretching sheet with energy dissipation, internal heat source and thermal radiation. Int J Heat Mass Transf 53(19):4264–4273

    Article  MATH  Google Scholar 

  25. Zeeshan A, Majeed A, Ellahi R (2016) Effect of magnetic dipole on viscous ferro-fluid past a stretching surface with thermal radiation. J Mol Liq 215:549–554

    Article  Google Scholar 

  26. Bhatti MM, Zeeshan A, Ellahi R (2016) Study of heat transfer with nonlinear thermal radiation on sinusoidal motion of magnetic solid particles in a dusty fluid. J Theor Appl Mech 46(3):75–94

    Article  MathSciNet  Google Scholar 

  27. Magyari E, Pantokratoras A (2011) Note on the effect of thermal radiation in the linearized Rosseland approximation on the heat transfer characteristics of various boundary layer flows. Int Commun Heat Mass 38(5):554–556

    Article  Google Scholar 

  28. Abel S, Prasad KV, Mahaboob A (2005) Buoyancy force and thermal radiation effects in MHD boundary layer visco-elastic fluid flow over continuously moving stretching surface. Int J Therm Sci 44(5):465–476

    Article  Google Scholar 

  29. Hayat T, Mustafa M, Pop I (2010) Heat and mass transfer for Soret and Dufour’s effect on mixed convection boundary layer flow over a stretching vertical surface in a porous medium filled with a viscoelastic fluid. Commun Nonlinear Sci Numer Simul 15(5):1183–1196

    Article  MathSciNet  MATH  Google Scholar 

  30. Rashidi MM, Ali M, Rostami B, Rostami P, Xie GN (2015) Heat and mass transfer for MHD viscoelastic fluid flow over a vertical stretching sheet with considering soret and dufour effects. Math Probl Eng. https://doi.org/10.1155/2015/861065

    MathSciNet  Google Scholar 

  31. Jena S, Dash GC, Mishra SR (2016) Chemical reaction effect on MHD viscoelastic fluid flow over a vertical stretching sheet with heat source/sink. J, Ain Shams Eng. https://doi.org/10.1016/j.asej.2016.06.014

    Google Scholar 

  32. Neto C, Craig VS, Williams DR (2003) Evidence of shear-dependent boundary slip in Newtonian liquids. Eur Phys J E 12(1):71–74

    Article  Google Scholar 

  33. Churaev NV, Sobolev VD, Somov N (1984) Slippage of liquids over lyophobic solid surfaces. J Colloid Interface Sci 97:574–581

    Article  Google Scholar 

  34. Craig VSJ, Neto C, Williams DRM (2001) Shear-dependent boundary slip in an aqueous Newtonian liquid. Phys Rev Lett 87:054504

    Article  Google Scholar 

  35. Thompson PA, Troian SMA (1997) A general boundary condition for liquid flow at solid surfaces. Nature 389:360–362

    Article  Google Scholar 

  36. Ariel PD, Hayat T, Asghar S (2006) The flow of an elastico-viscous fluid past a stretching sheet with partial slip. Acta Mech 187(1–4):29–35

    Article  MATH  Google Scholar 

  37. Megahed AM (2016) Slip flow and variable properties of viscoelastic fluid past a stretching surface embedded in a porous medium with heat generation. J Cent South Univ 23(4):991–999

    Article  Google Scholar 

  38. Anand V (2016) Effect of slip on heat transfer and entropy generation characteristics of simplified Phan-Thien–Tanner fluids with viscous dissipation under uniform heat flux boundary conditions: exponential formulation. Appl Therm Eng 98:455–473

    Article  Google Scholar 

  39. Bataller RC (2008) Radiation effects for the Blasius and Sakiadis flows with a convective surface boundary condition. Appl Math Comput 206(2):832–840

    MathSciNet  MATH  Google Scholar 

  40. Aziz A (2009) A similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Commun Nonlinear Sci Numer Simul 14(4):1064–1068

    Article  Google Scholar 

  41. Ishak A (2010) Similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition. Appl Math Comput 217(2):837–842

    MathSciNet  MATH  Google Scholar 

  42. Yao S, Fang T, Zhong Y (2011) Heat transfer of a generalized stretching/shrinking wall problem with convective boundary conditions. Commun Nonlinear Sci Numer Simul 16(2):752–760

    Article  MATH  Google Scholar 

  43. Das K, Acharya N, Kundu PK (2016) The onset of nanofluid flow past a convectively heated shrinking sheet in presence of heat source/sink: a Lie group approach. Appl Therm Eng 103:38–46

    Article  Google Scholar 

  44. Davidson PA (2001) An introduction to magnetohydrodynamics. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  45. Seth GS, Sharma R, Mishra MK, Chamkha AJ (2017) Analysis of hydromagnetic natural convection radiative flow of a viscoelastic nanofluid over a stretching sheet with Soret and Dufour effects. Eng Comput 34(2):603–628

    Article  Google Scholar 

  46. Coleman BD, Noll w (1960) An approximation theorem for functionals, with applications in continuum mechanics. Archs Ration Mech Anal 6:355–370

    Article  MathSciNet  MATH  Google Scholar 

  47. Reddy JN, Gartling DK (2010) The finite element method in heat transfer and fluid dynamics. CRC Press Taylor and Francis Group, New York

    MATH  Google Scholar 

Download references

Acknowledgements

We are grateful to learned reviewers for their valuable suggestions which helped us to improve the quality of this research paper.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Indian Institute of Technology (Indian School of Mines), Dhanbad, 826004, India

    G. S. Seth, M. K. Mishra & R. Tripathi

Authors
  1. G. S. Seth
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. K. Mishra
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. R. Tripathi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. S. Seth.

Additional information

Techncial Editor: Cezar Negrao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Seth, G.S., Mishra, M.K. & Tripathi, R. MHD free convective heat transfer in a Walter’s liquid-B fluid past a convectively heated stretching sheet with partial wall slip. J Braz. Soc. Mech. Sci. Eng. 40, 103 (2018). https://doi.org/10.1007/s40430-018-1028-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1028-5

Keywords

Search

Navigation