Skip to main content
SpringerLink
Log in

Nonlinear convection flow of micropolar liquid: an application of improved Fourier’s expression

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

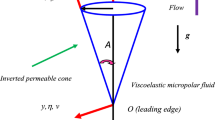
Here, improved Fourier’s expression is utilized for heat transfer in nonlinear convection flow of micropolar liquid. The flow is generated due to a stretchable surface with variable thickness. Application of non-Fourier conduction phenomenon illustrates the characteristics of thermal relaxation factor. Temperature-dependent conductivity of liquid is also adopted. The set of partial differential equations governing the flow of micropolar liquid and heat transfer through non-Fourier heat conduction concept is established. The relevant transformations provide the highly nonlinear ordinary differential system. Homotopy theory is employed to acquire convergent solutions for nonlinear differential systems. Coefficient of skin friction is computed and examined for distinct embedded variables. Our presented analysis shows that temperature is decaying for larger thermal relaxation time.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Abbreviations

u, v :

Velocity components

x, y :

Space coordinates

U w (x):

Stretching velocity

U e (x):

Free stream velocity

U 0, U ∞ :

Reference velocities

N :

Micro-rotation variable

g :

Gravitational accelerational

β 1 :

Linear thermal expansion coefficient

β 2 :

Nonlinear thermal expansion coefficient

γ*:

Spin gradient viscosity

j :

Micro-inertia

m 0 :

Boundary parameter

q :

Heat flux

λ :

Relaxation time of heat flux

K(T):

Variable thermal conductivity

K ∞ :

Thermal conductivity of ambient fluid

μ :

Dynamic viscosity

ν :

Kinematic viscosity

ρ :

Fluid density

k :

Vortex viscosity

c p :

Specific heat

b :

Dimensional constant

T w :

Variable temperature at the sheet

T ∞ :

Variable temperature away from the sheet

δ :

Small parameter regarding the surface is sufficiently thin

K :

Micropolar parameter

λ :

Local buoyancy parameter

Gr x :

Local Grashof number

δ :

Nonlinear convection

Pr:

Prandtl number

γ :

Thermal relaxation parameter

α :

Wall thickness parameter

n :

Power law index

\(\in\) :

Temperature dependent thermal conductivity parameter

ψ :

Stream function

η :

Dimensionless variable

f(η):

Dimensionless velocity

g(η):

Dimensionless micro-rotation velocity

θ(η):

Dimensionless temperature

C f :

Skin friction coefficient

τ w :

Surface shear stress

Re x :

Local Reynolds number

f 0(η),g 0(η):

Initial approximations for velocity

θ 0(η):

Initial approximations for temperature

L f ,L g ,L θ :

Linear operators

C i :

Arbitrary constants

ℏ f , ℏ g , ℏ θ :

Auxiliary variables

References

  1. Eringen AC (1966) Theory of micropolar fluids. J Math Mech 16:1–18

    MathSciNet  Google Scholar 

  2. Lukaszewicz G (1999) Micropolar fluids: theory and applications. Brikhauser, Basel

    Book  MATH  Google Scholar 

  3. Eringen AC (2001) Microcontinuum field theories II: fluent media. Springer, New York

    MATH  Google Scholar 

  4. Rashad AM, Abbasbandy S, Chamkha AJ (2014) Mixed convection flow of a micropolar fluid over a continuously moving vertical surface immersed in a thermally and solutally stratified medium with chemical reaction. J Taiwan Inst Chem Eng 45:2163–2169

    Article  Google Scholar 

  5. Sandeep N, Sulochana C (2015) Dual solutions for unsteady mixed convection flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink. Eng Sci Technol Int J 18:738–745

    Article  Google Scholar 

  6. Shehzad SA, Waqas M, Alsaedi A, Hayat T (2016) Flow and heat transfer over an unsteady stretching sheet in a micropolar fluid with convective boundary condition. J Appl Fluid Mech 9:1437–1445

    Article  Google Scholar 

  7. Hayat T, Farooq S, Ahmad B, Alsaedi A (2016) Homogeneous-heterogeneous reactions and heat source/sink effects in MHD peristaltic flow of micropolar fluid with Newtonian heating in a curved channel. J Mol Liq 223:469–488

    Article  Google Scholar 

  8. Waqas M, Farooq M, Khan MI, Alsaedi A, Hayat T, Yasmeen T (2016) Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int J Heat Mass Transfer 102:766–772

    Article  Google Scholar 

  9. Turkyilmazoglu M (2017) Mixed convection flow of magnetohydrodynamic micropolar fluid due to a porous heated/cooled deformable plate: exact solutions. Int J Heat Mass Transfer 106:127–134

    Article  Google Scholar 

  10. Crane L (1970) Flow past a stretching plate. Z Angew Math Phys 21:645–647

    Article  Google Scholar 

  11. Turkyilmazoglu M (2015) An analytical treatment for the exact solutions of MHD flow and heat over two–three dimensional deforming bodies. Int J Heat Mass Transfer 90:781–789

    Article  Google Scholar 

  12. Turkyilmazoglu M (2016) Flow of a micropolar fluid due to a porous stretching sheet and heat transfer. Int J Non-Linear Mech 83:59–64

    Article  Google Scholar 

  13. Waqas M, Hayat T, Farooq M, Shehzad SA, Alsaedi A (2016) Cattaneo–Christov heat flux model for flow of variable thermal conductivity generalized Burgers fluid. J Mol Liq 220:642–648

    Article  Google Scholar 

  14. Turkyilmazoglu M (2016) Equivalences and correspondences between the deforming body induced flow and heat in two-three dimensions. Phys Fluids 28:043102

    Article  Google Scholar 

  15. Babu MJ, Sandeep N (2016) 3D MHD slip flow of a nanofluid over a slendering stretching sheet with thermophoresis and Brownian motion effects. J Mol Liq 222:1003–1009

    Article  Google Scholar 

  16. Khan MI, Waqas M, Hayat T, Alsaedi A (2017) A comparative study of Casson fluid with homogeneous–heterogeneous reactions. J Colloid Interface Sci 498:85–90

    Article  Google Scholar 

  17. Khan WA, Irfan M, Khan M, Alshomrani AS, Alzahrani AK, Alghamdi MS (2017) Impact of chemical processes on magneto nanoparticle for the generalized Burgers fluid. J Mol Liq 234:201–208

    Article  Google Scholar 

  18. Hayat T, Khan MI, Waqas M, Alsaedi A, Farooq M (2017) Numerical simulation for melting heat transfer and radiation effects in stagnation point flow of carbon-water nanofluid. Comp Methods Appl Mech Eng 315:1011–1024

    Article  MathSciNet  Google Scholar 

  19. Bilal S, Rehman KU, Malik MY, Hussain A, Khan M (2017) Effects of temperature dependent conductivity and absorptive/generative heat transfer on MHD three dimensional flow of Williamson fluid due to bidirectional non-linear stretching surface. Results Phys 7:204–212

    Article  Google Scholar 

  20. Hayat T, Waqas M, Khan MI, Alsaedi A (2017) Impacts of constructive and destructive chemical reactions in magnetohydrodynamic (MHD) flow of Jeffrey liquid due to nonlinear radially stretched surface. J Mol Liq 225:302–310

    Article  Google Scholar 

  21. Devi SPA, Prakash M (2015) Temperature dependent viscosity and thermal conductivity effects on hydromagnetic flow over a slendering stretching sheet. J Niger Math Soc 34:318–330

    Article  MathSciNet  MATH  Google Scholar 

  22. Hayat T, Hussain Z, Alsaedi A, Ahmad B (2017) Numerical study for slip flow of carbon–water nanofluids. Computer Methods Appl Mech Eng 319:366–378

    Article  MathSciNet  Google Scholar 

  23. Khan MI, Hayat T, Waqas M, Alsaedi A (2017) Outcome for chemically reactive aspect in flow of tangent hyperbolic material. J Mol Liq 230:143–151

    Article  Google Scholar 

  24. Hayat T, Khan MI, Waqas M, Alsaedi A (2017) Mathematical modeling of non-Newtonian fluid with chemical aspects: a new formulation and results by numerical technique. Colloids Surf A Physicochem Eng Asp 518:263–272

    Article  Google Scholar 

  25. Imran Khan M, Hayat T, Ijaz Khan M, Alsaedi A (2017) A modified homogeneous-heterogeneous reactions for MHD stagnation flow with viscous dissipation and Joule heating. Int J Heat Mass Transfer 113:310–317

    Article  Google Scholar 

  26. Hayat T, Ullah I, Alsaedi A, Farooq M (2017) MHD flow of Powell–Eyring nanofluid over a non-linear stretching sheet with variable thickness. Results Phys 7:189–196

    Article  Google Scholar 

  27. Hayat T, Khan MI, Farooq M, Alsaedi A, Waqas M, Yasmeen T (2016) Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int J Heat Mass Transfer 99:702–710

    Article  Google Scholar 

  28. Ijaz Khan M, Hayat T, Waqas M, Imran Khan M, Alsaedi A (2017) Impact of heat generation/absorption and homogeneous–heterogeneous reactions on flow of Maxwell fluid. J Mol Liq 233:465–470

    Article  Google Scholar 

  29. Hayat T, Qayyum S, Imtiaz M, Alsaedi A (2017) Radiative flow due to stretchable rotating disk with variable thickness. Results Phys 7:156–165

    Article  Google Scholar 

  30. Hayat T, Qayyum S, Alsaedi A, Ahmad B (2017) Magnetohydrodynamic (MHD) nonlinear convective flow of Walters-B nanofluid over a nonlinear stretching sheet with variable thickness. Int J Heat Mass Transfer 110:506–514

    Article  Google Scholar 

  31. Fourier J B J (1822) Théorie Analytique De La Chaleur, Paris

  32. Catteneo C (1958) A form of heat conduction equation which eliminates the paradox of instantaneous propagation. Comput Rendus 247:431–433

    Google Scholar 

  33. Vernotte P (1958) Les paradoxes de la theorie continue de L’equation de lachaleur. Comput Rendus 246:3154–3155

    MathSciNet  MATH  Google Scholar 

  34. Christov CI (2009) On frame indifferent formulation of the Maxwell-Cattaneo model of finite speed heat conduction. Mech Res Commun 36:481–486

    Article  MathSciNet  MATH  Google Scholar 

  35. Straughan B (2011) Thermal convection with the Cattaneo–Christov model. Int J Heat Mass Transfer 53:95–98

    Article  MATH  Google Scholar 

  36. Tibullo V, Zampoli V (2011) A uniqueness result for the Cattaneo–Christov heat conduction model applied to incompressible fluids. Mech Res Commun 38:77–99

    Article  MATH  Google Scholar 

  37. Han S, Zheng L, Li C, Zhang X (2014) Coupled flow and heat transfer in viscoelastic fluid with Cattaneo–Christov heat flux model. Appl Math Lett 38:87–93

    Article  MathSciNet  MATH  Google Scholar 

  38. Hayat T, Waqas M, Shehzad SA, Alsaedi A (2016) On 2D stratified flow of an Oldroyd-B fluid with chemical reaction: an application of non-Fourier heat flux theory. J Mol Liq 223:566–571

    Article  Google Scholar 

  39. Khan WA, Khan M, Alshomrani AS, Ahmad L (2016) Numerical investigation of generalized Fourier’s and Fick’s laws for Sisko fluid flow. J Mol Liq 224:1016–1021

    Article  Google Scholar 

  40. Nadeem S, Muhammad N (2016) Impact of stratification and Cattaneo–Christov heat flux in the flow saturated with porous medium. J Mol Liq 224:423–430

    Article  Google Scholar 

  41. Hayat T, Khan MI, Waqas M, Alsaedi A (2017) On Cattaneo–Christov heat flux in the flow of variable thermal conductivity Eyring–Powell fluid. Results Phys 7:446–450

    Article  Google Scholar 

  42. Khan M, Ahmad L, Khan WA, Alshomrani AS, Alzahrani AK, Alghamdi MS (2017) A 3D Sisko fluid flow with Cattaneo–Christov heat flux model and heterogeneous-homogeneous reactions: a numerical study. J Mol Liq 238:19–26

    Article  Google Scholar 

  43. Zhang Y, Chen B, Li D (2017) Non-Fourier effect of laser-mediated thermal behaviors in bio-tissues: a numerical study by the dual-phase-lag model. Int J Heat Mass Transfer 108:1428–1438

    Article  Google Scholar 

  44. Turkyilmazoglu M (2016) An effective approach for evaluation of the optimal convergence control parameter in the homotopy analysis method. Filomat 30:1633–1650

    Article  MathSciNet  MATH  Google Scholar 

  45. Shehzad SA, Hayat T, Alsaedi A, Chen B (2016) A useful model for solar radiation. Energy Ecol Environ 1:30–38

    Article  Google Scholar 

  46. Hayat T, Waqas M, Khan MI, Alsaedi A (2016) Analysis of thixotropic nanomaterial in a doubly stratified medium considering magnetic field effects. Int J Heat Mass Transfer 102:1123–1129

    Article  Google Scholar 

  47. Ellahi R, Hassan M, Zeeshan A (2016) Aggregation effects on water base Al2O3-nanofluid over permeable wedge in mixed convection. Asia-Pac J Chem Eng 11:179–186

    Article  Google Scholar 

  48. Hayat T, Zubair M, Waqas M, Alsaedi A, Ayub M (2017) Application of non-Fourier heat flux theory in thermally stratified flow of second grade liquid with variable properties. Chin J Phys 55:230–241

    Article  Google Scholar 

  49. Khan WA, Alshomrani AS, Khan M (2016) Assessment on characteristics of heterogeneous-homogenous processes in three-dimensional flow of Burgers fluid. Results Phys 6:772–779

    Article  Google Scholar 

  50. Muhammad T, Alsaedi A, Shehzad SA, Hayat T (2017) A revised model for Darcy–Forchheimer flow of Maxwell nanofluid subject to convective boundary condition. Chin J Phys. https://doi.org/10.1016/j.cjph.2017.03.006

    Google Scholar 

  51. Turkyilmazoglu M (2016) Determination of the correct range of physical parameters in the approximate analytical solutions of nonlinear equations using the Adomian decomposition method. Mediterr J Math 13:4019–4037

    Article  MathSciNet  MATH  Google Scholar 

  52. Mahapatra TR, Gupta AS (2002) Heat transfer in stagnation-point flow towards a stretching sheet. Heat Mass Transfer 38:517–521

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Quaid-i-Azam University, Islamabad, 45320, Pakistan

    T. Hayat, M. Zubair, M. Waqas & M. Ayub

  2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, P. O. Box 80257, Jeddah, 21589, Saudi Arabia

    T. Hayat & A. Alsaedi

Authors
  1. T. Hayat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Zubair
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Waqas
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. Ayub
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. A. Alsaedi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Waqas.

Additional information

Technical Editor: Jader Barbosa Jr.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hayat, T., Zubair, M., Waqas, M. et al. Nonlinear convection flow of micropolar liquid: an application of improved Fourier’s expression. J Braz. Soc. Mech. Sci. Eng. 40, 99 (2018). https://doi.org/10.1007/s40430-018-0984-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-0984-0

Keywords

Search

Navigation