Skip to main content
SpringerLink
Log in

Modeling and analysis of tooth surface roughness for internal gearing power honing gear

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

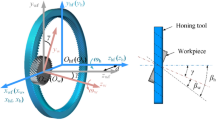
This paper describes mathematical modeling of tooth surface roughness of gear finished by internal gearing power honing (IGPH) process. The surface roughness of gear tooth was decomposed into two parts: (1) tooth profile roughness (R a-h), and (2) tooth longitudinal roughness (R a-l). Based on the machining mechanism of IGPH, the R a-h and R a-l models of involute spiral tooth surface were established considering general roughness theory and internal gearing generating movement between the honing wheel and the work-piece. With the proposed model, the R a-h and R a-l of tooth surface can be calculated as a distribution from tooth addendum to dedendum. The IGPH and roughness measurement experiments for the automobile transmission gear were carried out to verify the proposed roughness model. The theoretical values of R a-h and R a-l have shown close agreement with the experimental ones. The effect of the IGPH process parameters on roughness values and honing paths are discussed based on the proposed model, and proposing a control method for the stable IGPH quality based on the stable honing velocity. The results have shown that the crossed axis angle under 8° is not suitable for the scope of IGPH process.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Abbreviations

H EU :

The maximum height of groove calculated by E. Usui

τ :

The half cone angle of abrasive particle

v :

The velocity of the contact point on work-piece surface

V :

The velocity of the contact point on grinding wheel surface

d :

The curvature radius of the contact point on work-piece surface

D :

The curvature radius of the contact point on grinding wheel surface

Δ :

The average spacing between two adjacent abrasive particles

G :

The granularity of the abrasive particles

S :

The structure number of grinding wheel

h :

The height of plastic curvature

S a1 and S a2 :

The areas of plastic curvature

S a :

The area which ignores the effect of plastic curvature

c :

The compensation coefficient for plastic curvature

H :

The maximum height of groove considering the plastic curvature on work-piece surface

R a :

The roughness value on work-piece surface

w 1 :

The angular velocity of work-piece gear

w 2 :

The angular velocity of honing wheel

Z 1 :

The tooth number of work-piece gear

Z 2 :

The tooth number of honing wheel

β :

The helix angle of work-piece gear

m n :

The module of work-piece gear

v z :

The feed velocity of Z 1 axis

Σ :

The crossed axis angle between work-piece gear and honing wheel

φ 1 :

The rotation angle of work-piece gear

φ 2 :

The rotation angle of honing wheel

v O1 :

The velocity vector of the contact point on the tooth surface of work-piece gear

v O2 :

The velocity vector of the contact point on the tooth surface of honing wheel

v 12 :

The relative velocity vector of a random contact point in coordinate system S(O–x–y–z)

v 12h :

The relative velocity vector alone tooth profile direction

v 12l :

The relative velocity vector alone tooth longitudinal direction

v l :

The longitudinal direction velocity vector of contact point on work-piece gear tooth surface

V l :

The longitudinal direction velocity vector of contact point on honing wheel tooth surface

v h :

The profile direction velocity vector of contact point on work-piece gear tooth surface

V h :

The profile direction velocity vector of contact point on honing wheel tooth surface

w O1 :

The angular velocity vector of work-piece gear in coordinate system S(O–x–y–z)

w O2 :

The angular velocity vector of honing wheel in coordinate system S(O–x–y–z)

M OP :

The coordinate transmission matrix from S p(O p–x p–y p–z p) to S(O–x–y–z)

M O1 :

The coordinate transmission matrix from S 1(O 1–x 1–y 1–z 1) to S(O–x–y–z)

r O1 :

The position vector of contact points on work-piece gear tooth surface in coordinate system S(O–x–y–z)

r O2 :

The position vector of contact points on honing wheel tooth surface in coordinate system S(O–x–y–z)

t Oh :

The direction vector alone the tangent of involute at point M in coordinate system S(O–x–y–z)

t Ol :

The direction vector alone the tangent of helical line at point M in coordinate system S(O–x–y–z)

t h :

The direction vector alone the tangent of involute at point M in coordinate system S 1(O 1–x 1–y 1–z 1)

t l :

The direction vector alone the tangent of helical line at point M in coordinate system S 1(O 1–x 1–y 1–z 1)

R a-h :

Tooth profile roughness

R a-l :

Tooth longitudinal roughness

d l and D l :

The curvature radius of the contact point on work-piece surface and grinding wheel surface (tooth longitudinal)

d h and D h :

The curvature radius of the contact point on work-piece surface and grinding wheel surface (tooth profile)

r and R :

The radius values of work-piece gear and honing wheel at the contact point

p and p 2 :

The pitch of the helical line at the contact point

λ 1 :

The generating angle of involute at the contact point

r b1 :

The base circle radius of work-piece gear

α :

The pressure angle of work-piece gear

H EU-h :

The maximum height of gear profile groove

H EU-l :

The maximum height of gear longitudinal groove

H general-h :

The maximum gear profile groove height based on general theory

H general-l :

The maximum gear longitudinal groove height based on general theory

n :

The normal vector at the contact point

H generate-h :

The maximum groove height caused by the generated involute

H h :

The maximum groove height along gear profile direction

References

  1. Jolivet S, Mezghani S, Isselin J et al (2016) Experimental and numerical study of tooth finishing processes contribution to gear noise. Tribol Int 102:436–443

    Article  Google Scholar 

  2. Brandão JA, Seabra JHO, Castro MJD (2016) Surface fitting of an involute spur gear tooth flank roughness measurement to its nominal shape. Measurement 91:479–487

    Article  Google Scholar 

  3. Simon VV (2016) Micro tooth surface topography of face-milled hypoid gears. Mech Mach Theory 104:370–381

    Article  Google Scholar 

  4. Shaikh JH, Jain NK (2014) Modeling of material removal rate and surface roughness in finishing of bevel gears by electrochemical honing process. J Mater Process Technol 214(2):200–209

    Article  Google Scholar 

  5. Chen H, Tang J, Zhou W (2013) Modeling and predicting of surface roughness for generating grinding gear. J Mater Process Technol 213(5):717–721

    Article  Google Scholar 

  6. Wang YZ, Chen YY, Zhou GM et al (2016) Roughness model for tooth surfaces of spiral bevel gears under grinding. Mech Mach Theory 104:17–30

    Article  Google Scholar 

  7. Xianghan K, Xingzu M, Jing Z (2012) Modeling and experimental validation of spiral bevel gear grinding surface roughness. J Mech Transm 36(10):10–15

    Google Scholar 

  8. Yadong G, Yueming L, Jian C et al (2012) Research on simulation and experiment for workpiece micro-surface in point grinding. J Mech Eng 48(17):165–171

    Article  Google Scholar 

  9. Bin Y, Jiang H, Lulu W et al (2016) A prediction model and experimental study of gear hobbing profile errors based on particle swarm optimization. China Mech Eng 27(20):2705–2710

    Google Scholar 

  10. Unal O (2016) Optimization of shot peening parameters by response surface methodology. Surf Coat Technol 305:99–109

    Article  Google Scholar 

  11. Soundararajan R, Ramesh A, Mohanraj N et al (2016) An investigation of material removal rate and surface roughness of squeeze casted A413 alloy on WEDM by multi response optimization using RSM. J Alloys Compd 685:533–545

    Article  Google Scholar 

  12. Chen LQ, Guo JL, Yang X et al (2013) Grinding roughness prediction model based on evolutionary artificial neural network. Comput Integr Manuf Syst 19(11):2854–2863

    Google Scholar 

  13. Usui E (1971) Cutting and grinding processing, 1st edn. Kyoritsu Shuppan Co. Ltd. pressed, Tokyo

    Google Scholar 

  14. Malkin S (1989) Grinding technology: theory and applications of machining with abrasives. Ellis Horwood, England

    Google Scholar 

  15. Bigerelle M, Najjar D, Iost A (2003) Relevance of roughness parameters for describing and modelling machined surfaces. J Mater Sci 38(11):2525–2536

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the National Natural Science Foundation of China (51575154) and National Science and Technology Major Project (2013ZX04002051) for supporting this research under Grant.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Hefei University of Technology, Hefei, 230009, People’s Republic of China

    Bin Yuan, Jiang Han, Dongling Wang, Yonggang Zhu & Lian Xia

Authors
  1. Bin Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiang Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dongling Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yonggang Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Lian Xia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lian Xia.

Additional information

Technical Editor: Márcio Bacci da Silva.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yuan, B., Han, J., Wang, D. et al. Modeling and analysis of tooth surface roughness for internal gearing power honing gear. J Braz. Soc. Mech. Sci. Eng. 39, 3607–3620 (2017). https://doi.org/10.1007/s40430-017-0791-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40430-017-0791-z

Keywords

Search

Navigation