Skip to main content
SpringerLink
Log in

Simultaneous effects of magnetic field and convective condition in three-dimensional flow of couple stress nanofluid with heat generation/absorption

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

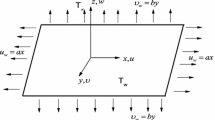
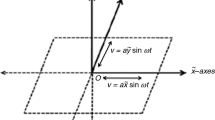
This work investigates the combined effects of heat generation/absorption and convective condition in magnetohydrodynamic (MHD) three-dimensional flow of couple stress nanofluid. The flow is because of a bidirectional stretching surface. Heat transfer mechanism is studied through the convective boundary condition. Problem formulation is developed in the presence of Brownian motion and thermophoresis. Couple stress fluid is electrically conducted subject to uniform applied magnetic field. Simultaneous effects of convective heat and zero nanoparticles mass flux conditions are utilized at the surface. Suitable transformations are employed to reduce the partial differential system into the nonlinear ordinary differential system. The resulting nonlinear system has been solved for the convergent series solutions. The temperature and nanoparticles concentration are discussed for various sundry variables. The skin friction coefficients and local Nusselt number are also computed and examined. Our computations reveal that the temperature distribution has a direct relationship with the Biot number and heat generation/absorption parameter. Further the temperature distribution and thermal boundary layer thickness are lower for Newtonian fluid in comparison to the couple stress fluid.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  1. Eringen AC (1966) Theory of micropolar fluids. J Math Mech 16:1–18

    MathSciNet  Google Scholar 

  2. Stokes VK (1966) Couple stresses in fluids. Phys Fluids 9:1709–1715

    Article  Google Scholar 

  3. Alsaedi A, Ali N, Tripathi D, Hayat T (2014) Peristaltic flow of couple stress fluid through uniform porous medium. Appl Math Mech 35:469–480

    Article  MathSciNet  Google Scholar 

  4. Turkyilmazoglu M (2014) Exact solutions for two-dimensional laminar flow over a continuously stretching or shrinking sheet in an electrically conducting quiescent couple stress fluid. Int J Heat Mass Transf 72:1–8

    Article  Google Scholar 

  5. Hayat T, Aziz A, Muhammad T, Ahmad B (2015) Influence of magnetic field in three-dimensional flow of couple stress nanofluid over a nonlinearly stretching surface with convective condition. PLoS One 10:e0145332

    Article  Google Scholar 

  6. Adesanya SO, Kareem SO, Falade JA, Arekete SA (2015) Entropy generation analysis for a reactive couple stress fluid flow through a channel saturated with porous material. Energy 93:1239–1245

    Article  Google Scholar 

  7. Ramesh K (2016) Influence of heat and mass transfer on peristaltic flow of a couple stress fluid through porous medium in the presence of inclined magnetic field in an inclined asymmetric channel. J Mol Liq 219:256–271

    Article  Google Scholar 

  8. Shit GC, Ranjit NK (2016) Role of slip velocity on peristaltic transport of couple stress fluid through an asymmetric non-uniform channel: application to digestive system. J Mol Liq 221:305–315

    Article  Google Scholar 

  9. Srinivasacharya D, Rao GM (2016) Mathematical model for blood flow through a bifurcated artery using couple stress fluid. Math Biosci 278:37–47

    Article  MathSciNet  MATH  Google Scholar 

  10. Ramesh K (2016) Effects of slip and convective conditions on the peristaltic flow of couple stress fluid in an asymmetric channel through porous medium. Comput Methods Programs Biomed 135:1–14

    Article  Google Scholar 

  11. Ashrafmansouri S, Esfahany MN (2014) Mass transfer in nanofluids: a review. Int J Therm Sci 82:84–99

    Article  Google Scholar 

  12. Das SK, Choi S, Yu W, Pradeep T (2007) Nanofluids: science and technology. Wiley, New Jersey

    Book  Google Scholar 

  13. Ozerinc S, Kakac S, Yazcoglu A (2010) Enhanced thermal conductivity of nanofluids: a state-of-the-art review. Microfluid Nanofluid 8:145–170

    Article  Google Scholar 

  14. Kleinstreuer C, Feng Y (2011) Experimental and theoretical studies of nanofluid thermal conductivity enhancement: a review. Nanoscale Res Lett 6:229

    Article  Google Scholar 

  15. Sundar LS, Sharma KV, Naik MT, Singh MK (2013) Empirical and theoretical correlations on viscosity of nanofluids: a review. Renew Sustain Energy Rev 25:670–686

    Article  Google Scholar 

  16. Buongiorno J (2006) Convective transport in nanofluids. ASME J Heat Transf 128:240–250

    Article  Google Scholar 

  17. Mustafa M, Hayat T, Pop I, Asghar S, Obaidat S (2011) Stagnation-point flow of a nanofluid towards a stretching sheet. Int J Heat Mass Transf 54:5588–5594

    Article  MATH  Google Scholar 

  18. Turkyilmazoglu M (2012) Exact analytical solutions for heat and mass transfer of MHD slip flow in nanofluids. Chem Eng Sci 84:182–187

    Article  Google Scholar 

  19. Malvandi, Ganji DD (2014) Mixed convective heat transfer of water/alumina nanofluid inside a vertical microchannel. Powder Tech 263:37–44

  20. Sheikholeslami M, Bandpy MG, Ellahi R, Hassan M, Soleimani S (2014) Effects of MHD on Cu-water nanofluid flow and heat transfer by means of CVFEM. J Magn Magn Mater 349:188–200

    Article  Google Scholar 

  21. Kuznetsov AV, Nield DA (2014) Natural convective boundary-layer flow of a nanofluid past a vertical plate: a revised model. Int J Therm Sci 77:126–129

    Article  Google Scholar 

  22. Malvandi A, Safaei MR, Kaffash MH, Ganji DD (2015) MHD mixed convection in a vertical annulus filled with Al2O3-water nanofluid considering nanoparticle migration. J Magn Magn Mater 382:296–306

    Article  Google Scholar 

  23. Hayat T, Muhammad T, Alsaedi A, Alhuthali MS (2015) Magnetohydrodynamic three-dimensional flow of viscoelastic nanofluid in the presence of nonlinear thermal radiation. J Magn Magn Mater 385:222–229

    Article  Google Scholar 

  24. Ellahi R, Hassan M, Zeeshan A (2015) Shape effects of nanosize particles in Cu-H2O nanofluid on entropy generation. Int J Heat Mass Transf 81:449–456

    Article  Google Scholar 

  25. Hayat T, Muhammad T, Shehzad SA, Chen GQ, Abbas IA (2015) Interaction of magnetic field in flow of Maxwell nanofluid with convective effect. J Magn Magn Mater 389:48–55

    Article  Google Scholar 

  26. Lin Y, Zheng L, Zhang X, Ma L, Chen G (2015) MHD pseudo-plastic nanofluid unsteady flow and heat transfer in a finite thin film over stretching surface with internal heat generation. Int J Heat Mass Transf 84:903–911

    Article  Google Scholar 

  27. Hayat T, Imtiaz M, Alsaedi A (2015) Impact of magnetohydrodynamics in bidirectional flow of nanofluid subject to second order slip velocity and homogeneous-heterogeneous reactions. J Magn Magn Mater 395:294–302

    Article  Google Scholar 

  28. Gireesha BJ, Gorla RSR, Mahanthesh B (2015) Effect of suspended nanoparticles on three-dimensional MHD flow, heat and mass transfer of radiating Eyring-Powell fluid over a stretching sheet. J Nanofluids 4:474–484

    Article  Google Scholar 

  29. Chamkha A, Abbasbandy S, Rashad AM (2015) Non-Darcy natural convection flow for non-Newtonian nanofluid over cone saturated in porous medium with uniform heat and volume fraction fluxes. Int J Numer Methods Heat Fluid Flow 25:422–437

    Article  MathSciNet  MATH  Google Scholar 

  30. Hayat T, Muhammad T, Qayyum A, Alsaedi A, Mustafa M (2016) On squeezing flow of nanofluid in the presence of magnetic field effects. J Mol Liq 213:179–185

    Article  Google Scholar 

  31. Mahanthesh B, Gorla RSR, Gireesha BJ (2016) Mixed convection squeezing three-dimensional flow in a rotating channel filled with nanofluid. Int J Numer Methods Heat Fluid Flow 26:1460–1485

    Article  MathSciNet  MATH  Google Scholar 

  32. Lin Y, Li B, Zheng L, Chen G (2016) Particle shape and radiation effects on Marangoni boundary layer flow and heat transfer of copper-water nanofluid driven by an exponential temperature. Powder Technol 301:379–386

    Article  Google Scholar 

  33. Hayat T, Abbas T, Ayub M, Farooq M, Alsaedi A (2016) Flow of nanofluid due to convectively heated Riga plate with variable thickness. J Mol Liq 222:854–862

    Article  Google Scholar 

  34. Hayat T, Muhammad T, Shehzad SA, Alsaedi A (2016) On three-dimensional boundary layer flow of Sisko nanofluid with magnetic field effects. Adv Powder Tech 27:504–512

    Article  Google Scholar 

  35. Hayat T, Aziz A, Muhammad T, Alsaedi A (2016) On magnetohydrodynamic three-dimensional flow of nanofluid over a convectively heated nonlinear stretching surface. Int J Heat Mass Transf 100:566–572

    Article  Google Scholar 

  36. Liao SJ (2004) On the homotopy analysis method for nonlinear problems. Appl Math Comput 147:499–513

    MathSciNet  MATH  Google Scholar 

  37. Dehghan M, Manafian J, Saadatmandi A (2010) Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer Meth Partial Diff Equ 26:448–479

    MathSciNet  MATH  Google Scholar 

  38. Turkyilmazoglu M (2012) Solution of the Thomas–Fermi equation with a convergent approach. Commun Nonlinear Sci Numer Simul 17:4097–4103

    Article  MathSciNet  MATH  Google Scholar 

  39. Turkyilmazoglu M (2012) An effective approach for approximate analytical solutions of the damped Duffing equation. Phys Scr 86:015301

    Article  MATH  Google Scholar 

  40. Sui J, Zheng L, Zhang X, Chen G (2015) Mixed convection heat transfer in power law fluids over a moving conveyor along an inclined plate. Int J Heat Mass Transf 85:1023–1033

    Article  Google Scholar 

  41. Hayat T, Muhammad T, Shehzad SA, Alsaedi A (2015) A mathematical study for three-dimensional boundary layer flow of Jeffrey nanofluid. Z Naturforsch A 70a:225–233

  42. Turkyilmazoglu M (2016) An effective approach for evaluation of the optimal convergence control parameter in the homotopy analysis method. Filomat 30:1633–1650

    Article  MathSciNet  Google Scholar 

  43. Ramzan M, Bilal M (2016) Three-dimensional flow of an elastico-viscous nanofluid with chemical reaction and magnetic field effects. J Mol Liq 215:212–220

    Article  Google Scholar 

  44. Hayat T, Waqas M, Khan MI, Alsaedi A (2016) Analysis of thixotropic nanomaterial in a doubly stratified medium considering magnetic field effects. Int J Heat Mass Transf 102:1123–1129

    Article  Google Scholar 

  45. Hayat T, Hussain Z, Muhammad T, Alsaedi A (2016) Effects of homogeneous and heterogeneous reactions in flow of nanofluids over a nonlinear stretching surface with variable surface thickness. J Mol Liq 221:1121–1127

    Article  Google Scholar 

  46. Ariel PD (2007) The three-dimensional flow past a stretching sheet and the homotopy perturbation method. Comp Math Appl 54:920–925

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Quaid-I-Azam University 45320, Islamabad, 44000, Pakistan

    Tasawar Hayat & Taseer Muhammad

  2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Faculty of Science, King Abdulaziz University, P. O. Box 80203, Jeddah, 21589, Saudi Arabia

    Tasawar Hayat & Ahmed Alsaedi

  3. Department of Mathematics, COMSATS Institute of Information Technology, Sahiwal, 57000, Pakistan

    Sabir Ali Shehzad

Authors
  1. Tasawar Hayat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Taseer Muhammad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sabir Ali Shehzad
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ahmed Alsaedi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sabir Ali Shehzad.

Additional information

Technical Editor: Jader Barbosa Jr.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hayat, T., Muhammad, T., Shehzad, S.A. et al. Simultaneous effects of magnetic field and convective condition in three-dimensional flow of couple stress nanofluid with heat generation/absorption. J Braz. Soc. Mech. Sci. Eng. 39, 1165–1176 (2017). https://doi.org/10.1007/s40430-016-0632-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40430-016-0632-5

Keywords

Search

Navigation