Skip to main content
SpringerLink
Log in

MHD forced convection and entropy generation of CuO-water nanofluid in a microchannel considering slip velocity and temperature jump

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

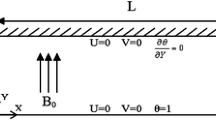
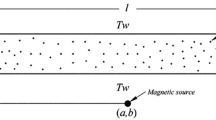
Flow field, heat transfer and entropy generation of forced convection of CuO-water nanofluid is investigated in a parallel plate microchannel in the presence of magnetic field. Two vertical micromixers are attached on the hot walls of the microchannel. To consider the effect of the Brownian motion of the nanoparticles, the KKL model is utilized to estimate thermal conductivity of the nanofluid. The governing equations, which are accompanied with the slip velocity and temperature jump boundary conditions, are solved by the finite volume method (FVM) and SIMPLER algorithm. The study is conducted for the Reynolds numbers in the range of 10 < Re < 100, Hartmann numbers in the range of 0 < Ha < 40, Knudsen numbers ranging of 0 < Kn < 0.1 and volume fraction of nanoparticles ranging of 0 < φ < 0.04. The results show that when the Hartmann or Reynolds numbers, or the volume fraction of nanoparticles increase, the average Nusselt number and the total entropy generation rate increase. Furthermore, when Knudsen number increases, the total entropy generation rate decreases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

a j :

Coefficient values of \(g^{\prime}\) function

B 0 :

Magnetic field intensity (N/m A)

c i :

Coefficients of fully developed velocity profile

c p :

Specific heat capacity (J/kg K)

d np :

Nanoparticles diameter (nm)

D h :

Hydraulic diameter (m)

h :

Local heat transfer coefficient (W/m2 K)

Ha:

Hartmann number

k :

Thermal conductivity (W/m K)

Kn:

Knudsen number

L :

Unit length (m)

n :

Unit normal vector

Nu:

Nusselt number

p :

Pressure (N/m2)

P :

Dimensionless pressure

Po:

Poiseuille number (≡f Re)

Pr:

Prandtl number

Re:

Reynolds number

R bf :

Thermal interfacial resistance (Km2/W)

\(\dot{s}^{\prime\prime\prime}\) :

Volumetric rate of entropy generation (W/m3 K)

\(\dot{S}^{\prime\prime\prime}\) :

Dimensionless volumetric rate of entropy generation

\(\dot{S}\) :

Dimensionless total rate of entropy generation

T :

Temperature (K)

(u,v) :

Velocity components (m/s)

(U,V) :

Dimensionless velocity components

(x,y) :

Coordinates (m)

(X,Y) :

Dimensionless coordinates

α :

Thermal diffusivity (m2/s)

γ :

Heat capacity ratio (≡ c p/c v)

θ :

Dimensionless temperature

κ b :

Boltzmann constant (=1.38064852 × 10−23 kg m2/s2 K)

λ :

Mean free path (m)

μ :

Dynamic viscosity (kg/m s)

ν :

Kinematic viscosity (m2/s)

ρ :

Density (kg/m3)

σ :

Electrical conductivity (1/Ω m = A2 s3/kg m3)

σ T :

Thermal accommodation coefficient

σ v :

Momentum accommodation coefficient

χ :

Irreversibility distribution ratio

\(\phi\) :

Nanoparticles volume fraction

0 :

Reference state value

av:

Average

bf:

Base fluid

Brownian:

Brownian motion component of thermal conductivity

eff:

Effective

fd:

Fully developed region

h :

Hot walls

in:

Inlet flow

nf:

Nanofluid

np:

Nanoparticles

static:

Static component of thermal conductivity

w :

Walls

References

  1. Yu S, Ameel TA (2001) Slip-flow heat transfer in rectangular microchannels. Int J Heat Mass Transf 44:4225–4234

    Article  MATH  Google Scholar 

  2. Renksizbulut M, Niazmand H, Tercan G (2006) Slip-flow and heat transfer in rectangular microchannels with constant wall temperature. Int J Therm Sci 45:870–881

    Article  Google Scholar 

  3. Zhu X, Liao Q (2006) Heat transfer for laminar slip flow in a microchannel of arbitrary cross section with complex thermal boundary conditions. Appl Therm Eng 26:1246–1256

    Article  Google Scholar 

  4. Barkhordari M, Etemad SG (2007) Numerical study of slip flow heat transfer of non-Newtonian fluids in circular microchannels. Int J Heat Fluid Flow 28:1027–1033

    Article  Google Scholar 

  5. Nayinian SMM, Shams M, Afshar H, Ahmadi G (2008) Two phase analysis of heat transfer and dispersion of nano particles in a microchannel. In: ASME 2008 Heat Transfer Summer Conference collocated with the Fluids Engineering, Energy Sustainability, and 3rd Energy Nanotechnology Conferences, pp 457–463

  6. Niazmand H, Renksizbulut M, Saeedi E (2008) Developing slip-flow and heat transfer in trapezoidal microchannels. Int J Heat Mass Transf 51:6126–6135

    Article  MATH  Google Scholar 

  7. Hooman K, Hooman F, Famouri M (2009) Scaling effects for flow in micro-channels: variable property, viscous heating, velocity slip, and temperature jump. Int Commun Heat Mass Transfer 36:192–196

    Article  Google Scholar 

  8. Shojaeian M, Dibaji SAR (2010) Three-dimensional numerical simulation of the slip flow through triangular microchannels. Int Commun Heat Mass Transfer 37:324–329

    Article  Google Scholar 

  9. Buonomo B, Manca O (2010) Natural convection slip flow in a vertical microchannel heated at uniform heat flux. Int J Therm Sci 49:1333–1344

    Article  Google Scholar 

  10. Languri EM, Hooman K (2011) Slip flow forced convection in a microchannel with semi-circular cross-section. Int Commun Heat Mass Transfer 38:139–143

    Article  Google Scholar 

  11. Adesanya SO (2015) Free convective flow of heat generating fluid through a porous vertical channel with velocity slip and temperature jump,” Ain Shams Engineering Journal

  12. Tuckerman DB, Pease R (1981) High-performance heat sinking for VLSI. Electron Device Lett IEEE 2:126–129

    Article  Google Scholar 

  13. Hettiarachchi HM, Golubovic M, Worek WM, Minkowycz W (2008) Three-dimensional laminar slip-flow and heat transfer in a rectangular microchannel with constant wall temperature. Int J Heat Mass Transf 51:5088–5096

    Article  MATH  Google Scholar 

  14. Shams M, Shojaeian M, Aghanajafi C, Dibaji S (2009) Numerical simulation of slip flow through rhombus microchannels. Int Commun Heat Mass Transfer 36:1075–1081

    Article  Google Scholar 

  15. Akbarinia A, Abdolzadeh M, Laur R (2011) Critical investigation of heat transfer enhancement using nanofluids in microchannels with slip and non-slip flow regimes. Appl Therm Eng 31:556–565

    Article  Google Scholar 

  16. Ebrahimi A, Roohi E, Kheradmand S (2015) Numerical study of liquid flow and heat transfer in rectangular microchannel with longitudinal vortex generators. Appl Therm Eng 78:576–583

    Article  Google Scholar 

  17. Karimipour A (2015) New correlation for Nusselt number of nanofluid with Ag/Al2O3/Cu nanoparticles in a microchannel considering slip velocity and temperature jump by using lattice Boltzmann method. Int J Therm Sci 91:146–156

    Article  Google Scholar 

  18. Abbassi H (2007) Entropy generation analysis in a uniformly heated micro-channel heat sink. Energy 32:1932–1947

    Article  Google Scholar 

  19. Guo J, Xu M, Tao Y, Huai X (2012) The effect of temperature-dependent viscosity on entropy generation in curved square micro-channel. Chem Eng Process 52:85–91

    Article  Google Scholar 

  20. Ibáñez G, López A, Pantoja J, Moreira J, Reyes JA (2013) Optimum slip flow based on the minimization of entropy generation in parallel plate micro-channels. Energy 50:143–149

    Article  Google Scholar 

  21. Ibáñez G, López A, Pantoja J, Moreira J (2014) Combined effects of uniform heat flux boundary conditions and hydrodynamic slip on entropy generation in a micro-channel. Int J Heat Mass Transf 73:201–206

    Article  Google Scholar 

  22. Anand V (2014) Slip law effects on heat transfer and entropy generation of pressure driven flow of a power law fluid in a micro-channel under uniform heat flux boundary condition. Energy 76:716–732

    Article  Google Scholar 

  23. Ting TW, Hung YM, Guo N (2014) Entropy generation of nanofluid flow with streamwise conduction in micro-channels. Energy 64:979–990

    Article  Google Scholar 

  24. Hooman K (2007) Entropy generation for microscale forced convection: effects of different thermal boundary conditions, velocity slip, temperature jump, viscous dissipation, and duct geometry. Int Commun Heat Mass Transfer 34:945–957

    Article  Google Scholar 

  25. Sohel M, Saidur R, Hassan N, Elias M, Khaleduzzaman S, Mahbubul I (2013) Analysis of entropy generation using nanofluid flow through the circular microchannel and minichannel heat sink. Int Commun Heat Mass Transfer 46:85–91

    Article  Google Scholar 

  26. Pourmahmoud N, Soltanipour H, Mirzaee I (2014) The effects of longitudinal ribs on entropy generation for laminar forced convection in a microchannel. Thermal Science, pp 110–110

  27. Hajialigol N, Fattahi A, Ahmadi MH, Qomi ME, Kakoli E (2015) MHD mixed convection and entropy generation in a 3-D microchannel using Al2O3–water nanofluid. J Taiwan Inst Chem Eng 46:30–42

    Article  Google Scholar 

  28. Aminossadati SM, Raisi A, Ghasemi B (2011) Effects of magnetic field on nanofluid forced convection in a partially heated microchannel. Int J Non Linear Mech 46:1373–1382

    Article  Google Scholar 

  29. Baheri Islami S, Dastvareh B, Gharraei R (2014) An investigation on the hydrodynamic and heat transfer of nanofluid flow, with non-Newtonian base fluid, in micromixers, International Journal of Heat and Mass Transfer 78:917–929

  30. Aghaei A, Khorasanizadeh H, Sheikhzadeh G, Abbaszadeh M (2016) Numerical study of magnetic field on mixed convection and entropy generation of nanofluid in a trapezoidal enclosure. J Magn Magn Mater 403:133–145

    Article  Google Scholar 

  31. Arefmanesh A, Aghaei A, Ehteram H (2016) Mixed convection heat transfer in a CuO–water filled trapezoidal enclosure, effects of various constant and variable properties of the nanofluid. Appl Math Model 40:815–831

    Article  MathSciNet  Google Scholar 

  32. Heidary H, Hosseini R, Pirmohammadi M, Kermani MJ (2015) Numerical study of magnetic field effect on nano-fluid forced convection in a channel. J Magn Magn Mater 374:11–17

    Article  Google Scholar 

  33. Mahian O, Kianifar A, Kleinstreuer C, A.-N. Moh’d A, Pop I, Sahin AZ, Wongwises S (2013) A review of entropy generation in nanofluid flow, International Journal of Heat and Mass Transfer 65:514–532

  34. Oueslati F, Ben-Beya B, Lili T (2013) Double-diffusive natural convection and entropy generation in an enclosure of aspect ratio 4 with partial vertical heating and salting sources. Alex Eng J 52:605–625

    Article  Google Scholar 

  35. Li J (2009) Computational Analysis of Nanofluid Flow in Microchannels with Applications to Micro-heat Sinks and Bio-MEMS, Ph.D. dissertation, MAE Department, NCSU, Raleigh, NC

  36. Koo J, Kleinstreuer C (2005) Laminar nanofluid flow in microheat-sinks. Int J Heat Mass Transf 48:2652–2661

    Article  MATH  Google Scholar 

  37. Brinkman HC (1952) The viscosity of concentrated suspensions and solution. J Chem Phys 20:571–581

    Article  Google Scholar 

Download references

Acknowledgments

The authors wish to thank the Energy Research Institute of the University of Kashan for their support regarding this research (Grant No. 55806).

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Kashan, Kashan, Iran

    Mahmoud Abbaszadeh, Ahmad Ababaei, Ali Akbar Abbasian Arani & Ali Abbasi Sharifabadi

Authors
  1. Mahmoud Abbaszadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ahmad Ababaei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ali Akbar Abbasian Arani
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ali Abbasi Sharifabadi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahmad Ababaei.

Additional information

Technical Editor: Francis HR Franca.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abbaszadeh, M., Ababaei, A., Abbasian Arani, A.A. et al. MHD forced convection and entropy generation of CuO-water nanofluid in a microchannel considering slip velocity and temperature jump. J Braz. Soc. Mech. Sci. Eng. 39, 775–790 (2017). https://doi.org/10.1007/s40430-016-0578-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40430-016-0578-7

Keywords

Search

Navigation