Skip to main content
SpringerLink
Log in

On the convergence of Newton-like MS method with dynamics and applications

  • Published:
SeMA Journal Aims and scope Submit manuscript

Abstract

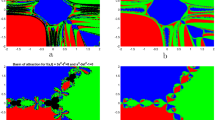
The motive of this work is to introduce and investigate the benefits and defects of a new three-step Newton-like iterative method to solve nonlinear operator equations in Banach space. We discussed the local and more importantly semi-local convergence analysis for the proposed method. Some numerical examples along with one boundary value problem are given to show that the speed of convergence of the proposed iterative method is faster than the modified Newton’s method and Sahu et al. method. Lastly, the dynamical analysis confirms the theoretical and numerical results, but reveals some drawback of this type of Newton-like S method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Agarwal, R.P., O’Regan, D., Sahu, D.R.: Fixed Point Theory for Lipschitzian-type Mappings with Applications. Topological Fixed Point Theory and its Applications, vol. 6. Springer, New York (2009)

  2. Amat, S., Busquier, S., Plaza, S.: Review of some iterative root-finding methods from a dynamical point of view. Scientia 10(3), 35 (2004)

    MathSciNet  MATH  Google Scholar 

  3. Argyros, I.K.: Convergence and Applications of Newton-type Iterations. Springer, Berlin (2008)

    MATH  Google Scholar 

  4. Argyros, I.K.: Computational Theory of Iterative Methods, Studies in Computational Mathematics, vol. 15. Elsevier Publ. Comp., New York (2007)

  5. Argyros, I.K., Magrenan, A.A.: Iterative Methods and Their Dynamics with Applications: A Contemporary Study. CRC Press, Taylor and Francis, Boca Raton (2017)

    Book  MATH  Google Scholar 

  6. Argyros, I.K., Ren, H.: On convergence of the modified Newton’s method under Holder continuous Frechet derivative. Appl. Math. Comput. 213, 440–448 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bartle, R.G.: Newton’s method in Banach spaces. Proc. Am. Math. Soc. 6, 827–831 (1955)

    MathSciNet  MATH  Google Scholar 

  8. Berinde, V.: Iterative Approximation of Fixed Points. Springer, Berlin (2007)

    MATH  Google Scholar 

  9. Dennis, J.E.: On the Kantorovich hypothesis for Newton’s method. SIAM J. Numer. Anal. 6, 493–507 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  10. Kreyszig, E.: Introductory Functional Analysis with Applications. Wiley, New York (1978)

    MATH  Google Scholar 

  11. Mandelbrot, B.B.: The Fractal Geometry of Nature. Macmillan. ISBN 978-0-7167-1186-5 (1983)

  12. Ortega, J., Rheinholdt, W.: Iterative Solution of Nonlinear Equations in Several Variables. Academic Press, New York (1970)

    Google Scholar 

  13. Rheinboldt, W.C.: A unified convergence theory for a class of iterative processes. SIAM J. Numer. Anal. 5, 42–63 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  14. Sahu, D.R.: Applications of the S-iteration process to constrained minimization problems and split feasibility problems. Fixed Point Theory 12, 187–204 (2011)

    MathSciNet  MATH  Google Scholar 

  15. Sahu, D.R., Singh, K.K., Singh, V.K.: Some Newton-like methods with sharper error estimates for solving operator equations in Banach spaces. Fixed Point Theory and Applications. Springer, pp. 1–20 (2012)

  16. Scott, M., Neta, B., Chun, C.: Basin attractors for various methods. Appl. Math. Comput. 218(2), 2584–2599 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  17. Singh, M.K.: A six-order variant of Newton’s method for solving non linear equations. Comput. Methods Sci. Technol. 15(2), 185–193 (2009)

    Article  Google Scholar 

  18. Singh, M.K., Singh, A.K.: An optimal 8th order Newton’s-type method with Basin of attraction. SeMA J. https://doi.org/10.1007/s40324-021-00262-1

  19. Suhubi, E.S.: Functional Analysis. Kluwer Academic Publishers, London (2003)

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Technology, Sardar Vallabhbhai Patel University of Agriculture and Technology, Meerut, 250110, India

    Manoj K. Singh, B. R. Singh & Deepak Kumar Mishra

Authors
  1. Manoj K. Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. B. R. Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Deepak Kumar Mishra
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Manoj K. Singh.

Ethics declarations

Conflict of interest

The authors declare there is no conflict of interest.

Ethical standards

This article does not contain any studies with animals performed by any of the authors. This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Singh, M.K., Singh, B.R. & Mishra, D.K. On the convergence of Newton-like MS method with dynamics and applications. SeMA 80, 663–686 (2023). https://doi.org/10.1007/s40324-022-00311-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40324-022-00311-3

Keywords

Mathematics Subject Classification

Search

Navigation