Skip to main content
SpringerLink
Log in

Extended convergence ball for an efficient eighth order method using only the first derivative

  • Published:
SeMA Journal Aims and scope Submit manuscript

Abstract

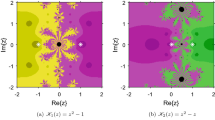
We develop an extended convergence ball for an efficient eighth order method to obtain numerical solutions of Banach space valued nonlinear models. Convergence of this algorithm has previously been shown using assumptions up to the ninth derivative. However, in our convergence theorem, we use only the first derivative. As a consequence, in contrast to previous ideas, the results on calculable error bounds, convergence radius and uniqueness zone for the solution are provided. Furthermore, this scheme is applied to several complex polynomials and related attraction basins are displayed. The results of numerical tests are presented and compared with the earlier technique. We arrive at the conclusion that the suggested analysis produces much larger convergence radii in all tests. Hence, we expand the convergence domain of this iterative formula.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Amat, S., Argyros, I..K., Busquier, S., Hernández-Verón, M..A., Martínez, E.: On the local convergence study for an efficient k-step iterative method. J. Comput. Appl. Math 343, 753–761 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  2. Amat, S., Busquier, S.: Advances in Iterative Methods for Nonlinear Equations. Springer, Cham (2016)

    Book  MATH  Google Scholar 

  3. Amiri, A., Cordero, A., Darvishi, M.T., Torregrosa, J.R.: Preserving the order of convergence: Low-complexity Jacobian-free iterative schemes for solving nonlinear systems. J. Comput. Appl. Math. 337, 87–97 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  4. Argyros, I.K.: Polynomial Operator Equations in Abstract Spaces and Applications. CRC Press, New York (1998)

    MATH  Google Scholar 

  5. Argyros, I.: Computational Theory of Iterative Methods. CRC Press, New York (2007)

    MATH  Google Scholar 

  6. Argyros, I.K.: Convergence and Application of Newton-type Iterations. Springer, Berlin (2008)

    MATH  Google Scholar 

  7. Argyros, I.K., George, S.: Local convergence for an efficient eighth order iterative method with a parameter for solving equations under weak conditions. Int. J. Appl. Comput. Math. 2, 565–574 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  8. Argyros, I.K., George, S.: Local convergence for an almost sixth order method for solving equations under weak conditions. SeMA J. 75(2), 163–171 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  9. Argyros, I.K., George, S.: On the complexity of extending the convergence region for Traub’s method. J. Complexity. 56, 101423 (2020). https://doi.org/10.1016/j.jco.2019.101423

    Article  MathSciNet  MATH  Google Scholar 

  10. Argyros, I.K., George, S., Erappa, S.M.: Ball convergence for an eighth order efficient method under weak conditions in Banach spaces. SeMA J. 74, 513–521 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  11. Argyros, I.K., Hilout, S.: Computational Methods in Nonlinear Analysis. World Scientific Publishing House, New Jersey (2013)

    Book  MATH  Google Scholar 

  12. Argyros, I.K., Magreñán, Á.A.: Iterative Methods and Their Dynamics with Applications: A Contemporary Study. CRC Press, New York (2017)

    Book  MATH  Google Scholar 

  13. Argyros, I.K., Magreñán, Á.A.: A Contemporary Study of Iterative Methods. Elsevier Academic Press, New York (2018)

    MATH  Google Scholar 

  14. Argyros, I.K., Sharma, D., Parhi, S.K., Sunanda, S.K.: On the convergence, dynamics and applications of a new class of nonlinear system solvers. Int. J. Appl. Comput. Math. 6(5), 142 (2020). https://doi.org/10.1007/s40819-020-00893-4

    Article  MathSciNet  MATH  Google Scholar 

  15. Cordero, A., Torregrosa, J.R.: Variants of Newtons method using fifth-order quadrature formulas. Appl. Math. Comput. 190, 686–698 (2007)

    MathSciNet  MATH  Google Scholar 

  16. Cordero, A., Villalba, E.G., Torregrosa, J.R., Triguero-Navarro, P.: Convergence and stability of a parametric class of iterative schemes for solving nonlinear systems. Mathematics 9(1), 1–19 (2021). https://doi.org/10.3390/math9010086

    Article  Google Scholar 

  17. Grau-Sánchez, M., Gutiérrez, J.M.: Zero-finder methods derived from Obreshkovs techniques. Appl. Math. Comput. 215, 2992–3001 (2009)

    MathSciNet  MATH  Google Scholar 

  18. Grau-Sánchez, M., Noguera, M., Amat, S.: On the approximation of derivatives using divided difference operators preserving the local convergence order of iterative methods. J. Comput. Appl. Math. 237, 363–372 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  19. Hueso, J.L., Martínez, E., Torregrosa, J.R.: Third and fourth order iterative methods free from second derivative for nonlinear systems. Appl. Math. Comput. 211, 190–197 (2009)

    MathSciNet  MATH  Google Scholar 

  20. Kumar, D., Sharma, J.R., Jäntschi, L.: Convergence analysis and complex geometry of an efficient derivative-free iterative method. Mathematics 7(10), 1–11 (2019)

    Article  Google Scholar 

  21. Liu, T., Qin, X., Wang, P.: Local convergence of a family of iterative methods with sixth and seventh order convergence under weak condition. Int. J. Comput. Methods 16(8), 1850120 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  22. Magreñán, Á.A.: Different anomalies in a Jarratt family of iterative root-finding methods. Appl. Math. Comput. 233, 29–38 (2014)

    MathSciNet  MATH  Google Scholar 

  23. Neta, B., Scott, M., Chun, C.: Basins of attraction for several methods to find simple roots of nonlinear equations. Appl. Math. Comput. 218, 10548–10556 (2012)

    MathSciNet  MATH  Google Scholar 

  24. Ortega, J.M., Rheinholdt, W.C.: Iterative solution of nonlinear equations in several variables. Academic Press, New York (1970)

    Google Scholar 

  25. Petković, M.S., Neta, B., Petković, L., Dz̃unić, D.: Multipoint Methods for Solving Nonlinear Equations. Elsevier, Oxford (2013)

  26. Rall, L.B.: Computational Solution of Nonlinear Operator Equations. Robert E. Krieger, New York (1979)

    MATH  Google Scholar 

  27. Rheinboldt, W.C.: An adaptive continuation process for solving systems of nonlinear equations. In: Tikhonov, A.N., et al. (eds.) Mathematical Models and Numerical Methods, Pub 3, pp. 129–142. Warsaw, Banach Center (1977)

    Google Scholar 

  28. Saxena, A., Argyros, I.K., Jaiswal, J.P., Argyros, C., Pardasani, K.R.: On the local convergence of two-step Newton type method in Banach spaces under generalized lipschitz conditions. Mathematics 9(6), 669 (2021). https://doi.org/10.3390/math9060669

    Article  Google Scholar 

  29. Scott, M., Neta, B., Chun, C.: Basin attractors for various methods. Appl. Math. Comput. 218, 2584–2599 (2011)

    MathSciNet  MATH  Google Scholar 

  30. Sharma, J.R., Argyros, I.K., Kumar, S.: Ball convergence of an efficient eighth order iterative method under weak conditions. Mathematics 6, 260 (2018)

    Article  MATH  Google Scholar 

  31. Sharma, J.R., Arora, H.: Improved Newton-like methods for solving systems of nonlinear equations. SeMA J. 74, 147–163 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  32. Sharma, J.R., Arora, H., Petković, M.S.: An efficient derivative free family of fourth order methods for solving systems of nonlinear equations. Appl. Math. Comput. 235, 383–393 (2014)

    MathSciNet  MATH  Google Scholar 

  33. Sharma, R., Gagandeep, Bahl, A.: Design and analysis of an efficient multi step iterative scheme for systems of nonlinear equations. J. Math. Anal. 12(2), 53–71 (2021)

    MathSciNet  Google Scholar 

  34. Sharma, D., Parhi, S.K.: Extending the applicability of a Newton-Simpson-like method. Int. J. Appl. Comput. Math. 6(3), 79 (2020). https://doi.org/10.1007/s40819-020-00832-3

    Article  MathSciNet  MATH  Google Scholar 

  35. Sharma, D., Parhi, S.K.: On the local convergence of higher order methods in Banach spaces. Fixed Point Theory 22(2), 855–870 (2021). https://doi.org/10.24193/fpt-ro.2021.2.55

    Article  MathSciNet  MATH  Google Scholar 

  36. Traub, J.F.: Iterative Methods for Solution of Equations. Prentice-Hall, Upper Saddle River (1964)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Cameron University, Lawton, OK, 73505, USA

    Ioannis K. Argyros

  2. Department of Mathematics, Kalinga Institute of Industrial Technology, Bhubaneswar, Odisha, 751024, India

    Debasis Sharma

  3. Department of Computing and Technology, Cameron University, Lawton, OK, 73505, USA

    Christopher I. Argyros

  4. Department of Mathematics, Fakir Mohan University, Balasore, Odisha, 756020, India

    Sanjaya Kumar Parhi

  5. Department of Mathematics, IIIT Bhubaneswar, Bhubaneswar, Odisha, 751003, India

    Shanta Kumari Sunanda

Authors
  1. Ioannis K. Argyros
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Debasis Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Christopher I. Argyros
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sanjaya Kumar Parhi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Shanta Kumari Sunanda
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Argyros, I.K., Sharma, D., Argyros, C.I. et al. Extended convergence ball for an efficient eighth order method using only the first derivative. SeMA 80, 319–331 (2023). https://doi.org/10.1007/s40324-022-00287-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40324-022-00287-0

Keywords

Mathematics Subject Classification

Search

Navigation