Prevalence-based modeling approach of schistosomiasis: global stability analysis and integrated control assessment

Abstract

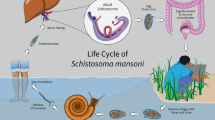
A system of nonlinear differential equations is proposed to assess the effects of prevalence-dependent disease contact rate, pathogen’s shedding rates, and treatment rate on the dynamics of schistosomiasis in a general setting. The decomposition techniques by Vidyasagar and the theory of monotone systems are the main ingredients to deal completely with the global asymptotic analysis of the system. Precisely, a threshold quantity for the analysis is derived and the existence of a unique endemic equilibrium is shown. Irrespective of the initial conditions, we prove that the solutions converge either to the disease-free equilibrium or to the endemic equilibrium, depending on whether the derived threshold quantity is less or greater than one. We assess the role of an integrated control strategy driven by human behavior changes through the incorporation of prevalence-dependent increasing the prophylactic treatment and decreasing the contact rate functions, as well as the mechanical water sanitation and the biological elimination of snails. Because schistosomiasis is endemic, the aim is to mitigate the endemic level of the disease. In this regard, we show both theoretically and numerically that: the reduction of contact rate through avoidance of contaminated water, the enhancement of prophylactic treatment, the water sanitation, and the removal of snails can reduce the endemic level and, to an ideal extent, drive schistosomiasis to elimination.

Appendixes

1.1 Appendix A: Proof of Corollary 1

Proof

We are going to prove that $\dfrac{\partial I^*_\mathrm{h}}{\partial \beta _\mathrm{M}} \le 0$. Recall the equilibrium equations:

$$\begin{aligned} \left\{ \begin{array}{l} \beta _\mathrm{h}(I^*_\mathrm{h})(N^*_\mathrm{h}-I^*_\mathrm{h})C^* - (d_\mathrm{h} + \gamma (I^*_\mathrm{h}))I^*_\mathrm{h} = 0,\\ \beta _\mathrm{s}(N^*_\mathrm{s}-I^*_\mathrm{s})M^* - (d_\mathrm{s} +\theta )I^*_\mathrm{s} = 0 ,\\ g(I^*_\mathrm{s}) -(d_\mathrm{c}+\eta )C^* = 0,\\ f(I^*_\mathrm{h}) - d_\mathrm{m} M^* = 0. \end{array}\right. \end{aligned}$$

(24)

In system (24), the fourth equation gives $M^* = \dfrac{f(I^*_\mathrm{h})}{d_\mathrm{m}}$, from which the first and second equations yield:

$$\begin{aligned} C^*= v(I^*_\mathrm{h}) = \dfrac{(d_\mathrm{h} + \gamma (I^*_\mathrm{h}))I^*_\mathrm{h}}{\beta _\mathrm{h}(I^*_\mathrm{h})(N^*_\mathrm{h}-I^*_\mathrm{h})}, \end{aligned}$$

(25)

and

$$\begin{aligned} I^*_\mathrm{s} = u(I^*_\mathrm{h}) = \dfrac{\beta _\mathrm{s} N^*_\mathrm{s} f(I^*_\mathrm{h})}{\beta _\mathrm{s}f(I^*_\mathrm{h})+d_\mathrm{m}(d_\mathrm{s}+\theta )}. \end{aligned}$$

(26)

Putting the two expressions above into the third equation of (24), yields another expression of $v(I^*_\mathrm{h})$ in the form, one has:

$$\begin{aligned} v(I^*_\mathrm{h}) = \dfrac{d_\mathrm{c} +\eta }{g(u(I^*_\mathrm{h}))}. \end{aligned}$$

(27)

Recalling from (1) that $\beta _\mathrm{h}(I^*_\mathrm{h}) = \beta _0 - \beta _\mathrm{M} \widetilde{\beta _\mathrm{h}}(I^*_\mathrm{h})$, $v(I^*_\mathrm{h})$ in (25) becomes:

$$\begin{aligned} v(I^*_\mathrm{h}) = \dfrac{(d_\mathrm{h} + \gamma (I^*_\mathrm{h}))I^*_\mathrm{h}}{(N^*_\mathrm{h}-I^*_\mathrm{h})\left[ \beta _0 - \beta _\mathrm{M} \widetilde{\beta _\mathrm{h}}(I^*_\mathrm{h})\right] }. \end{aligned}$$

Thus, the $I^*_\mathrm{h}$-component of the endemic equilibrium $E^*$ is the solution of:

$$\begin{aligned} \dfrac{(d_\mathrm{h} + \gamma (I^*_\mathrm{h}))I^*_\mathrm{h}}{(N^*_\mathrm{h}-I^*_\mathrm{h})\left[ \beta _0 - \beta _\mathrm{M} \widetilde{\beta _\mathrm{h}}(I^*_\mathrm{h})\right] } = \dfrac{d_\mathrm{c} +\eta }{g(u(I^*_\mathrm{h}))}. \end{aligned}$$

(28)

After differentiating both sides of (28) with respect to $\beta _\mathrm{M}$ using the chain rule, follow by some rearrangements, one has:

$$\begin{aligned}&\dfrac{\partial I^*_\mathrm{h}}{\partial \beta _\mathrm{M}} \left\{ \dfrac{W(I^*_\mathrm{h}) }{\left[ \beta _0 - \beta _\mathrm{M} \widetilde{\beta _\mathrm{h}}(I^*_\mathrm{h})\right] ^2(N^*_\mathrm{h}-I^*_\mathrm{h})^2} + \dfrac{(d_\mathrm{c} +\eta )g' (u(I^*_\mathrm{h}))u'(I^*_\mathrm{h})}{g^2(u(I^*_\mathrm{h}))}\right\} \nonumber \\&\quad = -\, \dfrac{ I^*_\mathrm{h}\left[ d_\mathrm{h}+ \gamma (I^*_\mathrm{h}) \right] \widetilde{\beta _\mathrm{h}}(I^*_\mathrm{h}) }{\left[ \beta _0 - \beta _\mathrm{M} \widetilde{\beta _\mathrm{h}}(I^*_\mathrm{h})\right] ^2(N^*_\mathrm{h}-I^*_\mathrm{h})}, \end{aligned}$$

(29)

where:

$$\begin{aligned} W(I^*_\mathrm{h})= & {} \left[ d_\mathrm{h} + \gamma (I^*_\mathrm{h})\right] \left[ (N^*_\mathrm{h}-I^*_\mathrm{h})\beta _\mathrm{h}(I^*_\mathrm{h}) + I^*_\mathrm{h} \beta _\mathrm{h}(I^*_\mathrm{h}) + \beta _\mathrm{M} I^*_\mathrm{h} (N^*_\mathrm{h}-I^*_\mathrm{h}) {\widetilde{\beta _\mathrm{h}}}'(I_\mathrm{h}) \right] \\&+ I^*_\mathrm{h}(N^*_\mathrm{h}-I^*_\mathrm{h})\beta _\mathrm{h}(I^*_\mathrm{h}) \gamma '(I^*_\mathrm{h}). \end{aligned}$$

Have in mind that, from (26), one has:

$$\begin{aligned} u'(I^*_\mathrm{h}) = \dfrac{\mathrm{d} u(I^*_\mathrm{h})}{\mathrm{d} I^*_\mathrm{h}} = \dfrac{\beta _\mathrm{s} N^*_\mathrm{s} d_\mathrm{m} f'(I^*_\mathrm{h}) (d_\mathrm{s}+\theta )}{\left[ \beta _\mathrm{s}f(I^*_\mathrm{h})+d_\mathrm{m}(d_\mathrm{s}+\theta )\right] ^2}. \end{aligned}$$

Since f, g and $\widetilde{\beta _\mathrm{h}}(I^*_\mathrm{h})$ are increasing, we have $u'(I^*_\mathrm{h}), W(I^*_\mathrm{h}) \ge 0$, so that the right-hand side of (29) is negative and the expression into the big brackets on the left-hand side of (29) is positive. Hence, the proof is achieved.

1.2 Appendix B: A primer on graph theory and monotone dynamical systems

1.2.1 A primer on graph theory

Definition B1 (Berman and Plemmons 1979, page 29) For a $n\times n$ matrix $A= \left( a_{ij}\right) _{1\le i, j\le n}$, the directed graph G(A) consists of $P_1,P_2, ... ,P_n$ vertices where an edge leads from $P_i$, to $P_j$ if and only if $a_{ij}\ne 0$.

Definition B2 (Berman and Plemmons 1979, page 30) A directed graph G(A) is strongly connected if, for any ordered pair $(P_i,P_j), i\ne j$ of vertices of G(A), there exists a sequence of edges (a path) which leads from $P_i$ to $P_j$.

Theorem B1 (Berman and Plemmons 1979, Theorem (2.7), page 31) A matrix A is irreducible if and only if G(A) is strongly connected.

1.2.2 A primer on monotone dynamical systems

Consider an ordinary differential equation (ODE):

$$\begin{aligned} \dfrac{\mathrm{d}x}{\mathrm{d}t} = f(x), \end{aligned}$$

(30)

defined on a positively invariant set U. We denote by $\Phi _t (x)$ the flow of (30). We assume, to avoid complications, that this is defined for any $t\ge 0$ (this will be the case our system). We consider the standard partial order on $\mathbb R^n$ and recall the following corresponding notations:

$$\begin{aligned}&x \le y \Longleftrightarrow \text{ for } \text{ all } \; i \; x_i \le y_i;\\&x < y \;\text{ if } \; x \le y \; \text{ and } \; x \ne y;\\&x \ll y \Longleftrightarrow \text{ for } \text{ all } \; i \; x_i \le y_i. \end{aligned}$$

Definition B3 (Hirsch 1988; Iggidr et al. 2012) System (1) is called monotone if $x \le y$ implies $\Phi _t(x) \le \Phi _t(y)$.

Definition B4 (Hirsch 1985; Iggidr et al. 2012) System (2) is called strongly monotone if $x < y$ implies $\Phi _t(x) \ll \Phi _t(y)$ for any $t > 0.$

Theorem B4 ((Smith 1988; Sokolowa et al. 2015), Lemma 2.1) If f is $C^1$, then System (1) is monotone if and only if the Jacobian of f is a Metzler matrix. Note that a Metzler matrix is a matrix whose off-diagonal terms are nonnegative.

Theorem B5 (Hirsch 1988; Iggidr et al. 2012) System (2) is strongly monotone if its Jacobian matrix is irreducible.

Definition B5 (Berman and Plemmons 1979, page 138) A matrix A has a regular splitting/decomposition if A has a representation $A= M-N$, where $M^{-1} \ge 0$, $N \ge 0$.