Skip to main content
SpringerLink
Log in

Numerical approach based on fractional-order Lagrange polynomials for solving a class of fractional differential equations

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

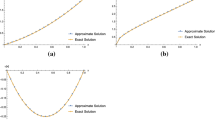
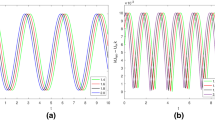
Abstract

In this study, we propose a new set of fractional functions based on the Lagrange polynomials to solve a class of fractional differential equations. Fractional differential equations are the best tools for modelling natural phenomenon that are elaborated by fractional calculus. Therefore, we need an accurate and efficient technique for solving them. The main purpose of this article is to generalize new functions based on Lagrange polynomials to the fractional calculus. At first, we present a new representation of Lagrange polynomials and in continue, we propose a new set of fractional-order functions which are called fractional-order Lagrange polynomials (FLPs). Besides, a general formulation for operational matrices of fractional integration and derivative of FLPs on arbitrary nodal points are extracted. These matrices are obtained using Laplace transform. The initial value problems is reduced to the system of algebraic equations using the operational matrix of fractional integration and collocation method. Also, we find the upper bound of error vector for the fractional integration operational matrix and we indicate convergence of approximations of FLPs. Illustrative examples are included to demonstrate the validity and applicability of the proposed technique.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Abd-Elhameed WM, Youssri YH (2017) Fifth-kind orthonormal Chebyshev polynomial solutions for fractional differential equations. Comput Appl Math 1–25. https://doi.org/10.1007/s40314-017-0488-z

  • Baillie RT (1996) Long memory processes and fractional integration in econometrics. J Econ 73:5–59

    Article  MathSciNet  MATH  Google Scholar 

  • Benson DA, Meerschaert MM, Revielle J (2013) Fractional calculus in hydrologic modeling: a numerical perspective. Adv Water Resour 51:479–497

    Article  Google Scholar 

  • Bhrawy AH, Alhamed YA, Baleanu D (2014) New spectral techniques for systems of fractional differential equations using fractional-order generalized Laguerre orthogonal functions. Fract Calc Appl Anal 17:1138–1157

    Article  MathSciNet  MATH  Google Scholar 

  • Bohannan GW (2008) Analog fractional order controller in temperature and motor control applications. J Vib Control 14:1487–1498

    Article  MathSciNet  Google Scholar 

  • Burden RL, Faires JD (2010) Numerical analysis, 9th edn. Brooks/Cole Cengage Learning, Boston

    MATH  Google Scholar 

  • Daftardar-Gejji V, Jafari H (2007) Solving a multi-order fractional differential equation using Adomian decomposition. Appl Math Comput 189:541–548

    MathSciNet  MATH  Google Scholar 

  • Dehghan M, Manafian J, Saadatmandi A (2010) Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer Methods Partial Differ Equ 26:448–479

    MathSciNet  MATH  Google Scholar 

  • Diethelm K, Ford NJ, Freed AD (2002) A predictorcorrector approach for the numerical solution of fractional differential equation. Nonlinear Dyn 29:3–22

    Article  MATH  Google Scholar 

  • Engheta N (1996) On fractional calculus and fractional multipoles in electromagnetism. IEEE Tran Antennas Propag 44:554–566

    Article  MathSciNet  MATH  Google Scholar 

  • Foroozandeh Z, Shamsi M (2012) Solution of nonlinear optimal control problems by the interpolating scaling functions. Acta Astronaut 72:21–26

    Article  Google Scholar 

  • Hall MG, Barrick TR (2008) From diffusion-weighted MRI to anomalous diffusion imaging. Magn Reson Med 59:447–455

    Article  Google Scholar 

  • Hashim I, Abdulaziz O, Momani S (2009) Homotopy analysis method for fractional IVPs. Commun Nonlinear Sci Numer Simul 14:674–684

    Article  MathSciNet  MATH  Google Scholar 

  • He JH (1988) Nonlinear oscillation with fractional derivative and its applications. In: Proceedings of the international conference on vibrating engineering. Dalian, China

  • Jafari H, Yousefi SA, Firoozjaee MA, Momani S, Khalique CM (2011) Application of Legendre wavelets for solving fractional differential equations. Comput Math Appl 62:1038–1045

    Article  MathSciNet  MATH  Google Scholar 

  • Javidi M, Ahmad B (2013) Numerical solution of fractional partial differential equations by numerical Laplace inversion technique. Adv Differ Equ 1:375. https://doi.org/10.1186/1687-1847-2013-375

  • Kazem S, Abbasbandy S, Kumar S (2013) Fractional-order Legendre functions for solving fractional-order differential equations. Appl Math Model 37:5498–551

    Article  MathSciNet  Google Scholar 

  • Keshavarz E, Ordokhani Y, Razzaghi M (2014) Bernoulli wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl Math Model 38:6038–6051

    Article  MathSciNet  Google Scholar 

  • Kreyszig E (1978) Introductory functional analysis with applications. Wiley, New York

    MATH  Google Scholar 

  • Krishnasamy VS, Razzaghi M (2016) The numerical solution of the Bagley–Torvik equation with fractional Taylor method. J Comput Nonlinear Dyn. https://doi.org/10.1115/1.4032390

  • Lakestani M, Dehghan M, Irandoust-pakchin S (2012) The construction of operational matrix of fractional derivatives using B-spline functions. Commun Nonlinear Sci Numer Simul 17:1149–1162

    Article  MathSciNet  MATH  Google Scholar 

  • Larsson S, Racheva M, Saedpanah F (2015) Discontinuous Galerkin method for an integro-differential equation modeling dynamic fractional order viscoelasticity. Comput Methods Appl Mechan Eng 283:196–209

    Article  MathSciNet  Google Scholar 

  • Magin RL (2004) Fractional calculus in bioengineering. Criti Rev Biomed Eng 32:1–104

    Article  Google Scholar 

  • Mainardi F (1997) Fractional calculus: some basic problems in continuum and statistical mechanics. Springer, New York

    Book  MATH  Google Scholar 

  • Mashayekhi S, Razzaghi M (2016) Numerical solution of distributed order fractional differential equations by hybrid functions. J Comput Phys 315:169–181

    Article  MathSciNet  MATH  Google Scholar 

  • Meerschaert MM, Tadjeran C (2006) Finite difference approximations for two-sided space-fractional partial differential equations. Appl Numer Math 56:80–90

    Article  MathSciNet  MATH  Google Scholar 

  • Miller KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations. Wiley, New York

    MATH  Google Scholar 

  • Mustafa MM, Ghanim IN (2014) Numerical solution of linear Volterra–Fredholm Integral equations using Lagrange polynomials. Math Theory Model 5:137–146

    Google Scholar 

  • Odibat Z, Momani S (2006) Application of variational iteration method to nonlinear differential equations of fractional order. Int J Nonlinear Sci Numer Simul 1:15–27

    MathSciNet  Google Scholar 

  • Odibat Z, Shawagfeh NT (2007) Generalized Taylors formula. Appl Math Comput 186:286–293

    MathSciNet  MATH  Google Scholar 

  • Oldham KB, Spanier J (1974) The fractional calculus. Academic Press, New York

    MATH  Google Scholar 

  • Podlubny I (1999) Fractional differential equations. Academic Press, San Diego

    MATH  Google Scholar 

  • Rahimkhani P, Ordokhani Y, Babolian E (2016) Fractional-order Bernoulli wavelets and their applications. Appl Math Model 40:8087–8107

    Article  MathSciNet  Google Scholar 

  • Rashed MT (2004) Lagrange interpolation to compute the numerical solutions of differential, integral and integro-differential equations. Appl Math Comput 151:869–878

    MathSciNet  MATH  Google Scholar 

  • Rehman MU, Khan RA (2012) A numerical method for solving boundary value problems for fractional differential equations. Appl Math Model 36:894–907

    Article  MathSciNet  MATH  Google Scholar 

  • Rossikhin YA, Shitikova MV (1997) Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl Mech Rev 50:15–67

    Article  Google Scholar 

  • Saadatmandi A, Dehghan M (2010) A new operational matrix for solving fractional-order differential equations. Comput Math Appl 59:1326–1336

    Article  MathSciNet  MATH  Google Scholar 

  • Shahsavaran A (2011) Lagrange functions method for solving nonlinear Hammerstein Fredholm–Volterra integral equations. Appl Math Sci 49:2443–2450

    MathSciNet  MATH  Google Scholar 

  • Shamsi M, Razzaghi M (2004) Numerical solution of the controlled duffing oscillator by the interpolating scaling functions. J Electromagn Waves Appl 18:691–705

    Article  Google Scholar 

  • Stoer J, Bulirsch R (2002) Introduction to numerical analysis, 3rd edn. Springer, NewYork

    Book  MATH  Google Scholar 

  • Yuzbasi S (2013) Numerical solutions of fractional Riccati type differential equations by means of the Bernstein polynomials. Comput Appl Math 219:6328–6343

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Mathematical Sciences, Alzahra University, Tehran, Iran

    S. Sabermahani & Y. Ordokhani

  2. Department of Mathematics, Faculty of Mathematical Sciences, Shahid Beheshti University, Tehran, Iran

    S. A. Yousefi

Authors
  1. S. Sabermahani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Y. Ordokhani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. A. Yousefi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Y. Ordokhani.

Additional information

Communicated by José Tenreiro Machado.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sabermahani, S., Ordokhani, Y. & Yousefi, S.A. Numerical approach based on fractional-order Lagrange polynomials for solving a class of fractional differential equations. Comp. Appl. Math. 37, 3846–3868 (2018). https://doi.org/10.1007/s40314-017-0547-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40314-017-0547-5

Keywords

Mathematics Subject Classification

Search

Navigation