Skip to main content
SpringerLink
Log in

Numerical solution of time-fractional Black–Scholes equation

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

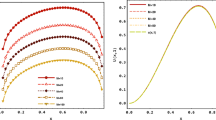
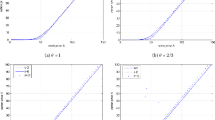
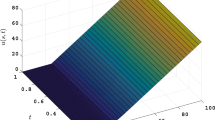
In this paper we present a numerical method for a time-fractional Black–Scholes equation, which is used for modeling the fractional structure of the financial market. The method is based on—first, discretization in time and then the weighted finite difference spatial approximation. Some properties of the spatial discretization are studied. The main difficulty (that originates from the non-local structure of the differential operator) of the algorithm is the impossibility to advance layer by layer in time. Numerical experiments are discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Achhdou Y, Pironneau O (2005) Computational methods for option pricing. SIAM, Philadelphia

    Book  Google Scholar 

  • Andersen L, Lipton, A (2012) Asymptotic for exponential Levy process and their volatility smile: survey and new results. arXiv:1206.6787v1 [q-fin.PR]

  • Elbeleze A, Kiliçman A, Taib B (2013) Homotopy perturbation method for fractional Black–Scholes European option pricing equations using Sumudu transform. Math Probl Eng. Article ID: 524852

  • Jumarie G (2008) Stock exchange fractional dynamics defined as fractional exponential growth driven by (usual) Gaussian white noise. Application to fractional Black-Scholes equations. Insur Math Econ 42:271–287

    Article  MATH  MathSciNet  Google Scholar 

  • Jumarie G (2010a) Derivation and solutions of some fractional Black–Scholes equations in coarse-grained space and time. Application to Merton’s optima portfolio. Comput Math Appl 59:1142–1164

    Article  MATH  MathSciNet  Google Scholar 

  • Jumarie G (2010b) Cauchy’s integral formula via the modified Riemann–Liouville derivative for analytic functions of fractional order. Appl Math Lett 23:1444–1450

    Article  MATH  MathSciNet  Google Scholar 

  • Kumar S, Yildirim A, Khan Y, Jafari H, Sayevand K, Wei L (2012) Analytical solution of a fractional Black–Scholes European option pricing equation by using Laplace transform. J Fract Calc Appl 2(8):1–9

    Google Scholar 

  • Liang J, Wang J, Zshang W, Qiu W, Ren F (2010) Option pricing of a bi-fractional Black–Merton–Scholes model with the Hurst exponent H in [1/2,1]. Appl Math Lett 10:859–863

    Article  MATH  MathSciNet  Google Scholar 

  • Merton RC (1974) On the pricing of corporate debt: the risk structure of interest rates. J Financ 29:449–470

    Google Scholar 

  • Miller KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations. Wiley, New York

    MATH  Google Scholar 

  • Podlubny I (1999) Fractional differential equations. Academic Press, San Diego

    MATH  Google Scholar 

  • Samarskii AA, Nikolaev ES (1978) Numerical methods for grid equations. Nauka, Moscow (in Russian)

  • Samko SG, Kilbas AA, Marichev OI (1987) Fractional integrals and derivatives. Theory and Applications. Gordon and Breach Science Publishers, London

    MATH  Google Scholar 

  • Sevcovic D, Stehlikova B, Mikula K (2011) Analytical and numerical methods for pricing financial derivatives. Nova Science Publishers Inc, Hauppauge

    Google Scholar 

  • Shen S, Liu F, Anh V, Turner I (2006) Detailed analysis of a conservative difference approximation for the time fractional diffusion equation. J Appl Math Comput 22(3):1–19

    Article  MATH  MathSciNet  Google Scholar 

  • Song L, Wang W (2013) Solution of the fractional Black–Scholes option pricing model by finite difference method. Abstr Appl Anal 2013:1–10. Article ID 194286

  • Wang X-T (2010) Scaling and long-range dependence in option pricing I: pricing European option with transaction costs under the fractional Black–Scholes model. Physica A 389:438–444

  • Wang J, Liang J, Lv L, Qiu W, Ren F (2012) Continuous time Black–Scholes equation with transaction costs in subdiffusive fractional Brownian motion regime. Physica A 391:750–763

    Article  MathSciNet  Google Scholar 

  • Wilmott P, Dewynne J, Howison S (1995) The mathematics of financial derivatives. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

Download references

Acknowledgments

The authors are grateful to the anonymous referees for their fruitful comments that improved the content of this manuscript. This research was supported by the European Union under Grant Agreement number 304617 (FP7 Marie Curie Action Project Multi-ITN STRIKE—Novel Methods in Computational Finance) and Bulgarian National Fund of Science under Project I02/20-2014.

Author information

Authors and Affiliations

  1. Department of Mathematics, Ruse University, 8 Studentska St., 7017, Ruse, Bulgaria

    Miglena N. Koleva

  2. Department of Numerical Methods and Statistics, Ruse University, 8 Studentska St., 7017, Ruse, Bulgaria

    Lubin G. Vulkov

Authors
  1. Miglena N. Koleva
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lubin G. Vulkov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Miglena N. Koleva.

Additional information

Communicated by Jorge Zubelli.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Koleva, M.N., Vulkov, L.G. Numerical solution of time-fractional Black–Scholes equation. Comp. Appl. Math. 36, 1699–1715 (2017). https://doi.org/10.1007/s40314-016-0330-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40314-016-0330-z

Keywords

Mathematics Subject Classification

Search

Navigation