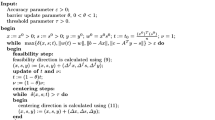1 Introduction

Given M\(\in{\mathbb{R}}^{n\times n} \) be the positive semidefinite matrix and \(q\in{\mathbb{R}}^{n}\), the monotone Linear Complementarity Problem (LCP) is to find a pair \((x,s)\in{\mathbb{R}}^{2n}\) such that

figure a

It is known that this problem trivially includes the two important domains in optimization: the linear optimization (LO) and the convex quadratic programming (QP) in their usual formulations, then this problem became the subject of many research interest. It is worth noting that there is a variety of solution approaches for LCP which have studied intensively. A close look at the IPM literature tells us that the first IPM for LCPs was due to Kojima, Mizuno and Yoshise [3] and their algorithm originated from the primal–dual IPMs for LO. Later Kojima et al. [4] set up a framework of IPMs for tracing the central path of a class of LCPs. It should be noted that all most known polynomial various of IPMs used the so-called central path as a guideline to optimal set, and some various of the Newton method to follow the central path approximately. Peng et al. [13, 14] who designed primal–dual feasible IPMs by using self-regular functions for LP and also extend the approach to LCP.

In very recently Mansouri et al. [8] introduced a new method for finding a class of search directions for feasible IPMs for LCPs. The complexity bound obtained by these authors is \(O(\sqrt{n}\log\frac{n}{\varepsilon})\), for small-update methods which coincides with the well-known best iteration bound for the feasible IPMs in LCPs.

All the above mentioned methods require a strictly feasible starting point. The assumption of the existence of a strictly feasible point, which implies the boundedness of the solution set. Finding an initial feasible interior point is the main difficulty for feasible IPMs. To overcome this difficulty we suggest algorithm that uses starting points that lie in the interior of the region defined by the inequality constraints, but do not satisfy the equality constraints. The points generated by the algorithm will remain in the interior of the region defined by the inequality constraints but will never satisfy exactly the equality constraints. This property is reflected in the name “Infeasible-Interior-Point Methods (IIPM)”, which has been suggested for such methods.

Lustig [6] and Tanabe [20, 21] were the first to present IIPMs for LP. Zhang [24] for the first time designed a primal–dual IIPM with polynomial complexity \(O(n^{2}\log\frac{1}{\varepsilon})\) for LP. Kojima, Mizuno and Todd [5], mention that the O(nL) infeasible interior-point algorithms for linear programming and then can be generalized for LCPs.

Potra [17] analyzed a generation to LCP of the Mizuno–Todd–Ye predictor corrector method [11] for infeasible starting points with O(nL) complexity. See also [15, 16]. Andersen et al. [1] presented a generalization of the homogeneous model for LP to solve the monotone complementarity problem for infeasible starting points with \(O(\sqrt{n}L)\) complexity. Recently Bai et al. [2] and Wang et al. [22] presented two IPMs for P ∗(k)-LCPs and P ∗(k)-HLCPs and they proved that the complexity of their algorithms coincide with the best known iteration bound for these kind of problems. In very recently, Mansouri et al. [10] presented the first full-Newton step IIPM for monotone LCP which is an extension of the work for LO by Roos [18].

In this paper, motivated by the complexity results for LO based on the study of Mansouri et al. [9] we extend their idea of LCP and show that the algorithm is faster convergent for problems having a strictly complementarity solution. To conclude this section we briefly describe how this article is organized. In Sect. 2, we study some basic concepts for feasible IPMs for solving LCPs, such as central path, full-Newton step, etc. In Sect. 3 we present the analysis of the feasibility step, which is the main part of this article. The analysis presented in this section differs from the analysis in [7, 9, 10, 23]. Some concluding remarks can be found in Sect. 4.

1.1 Notations

We use the following notations throughout the paper. Scalars and indices are denoted by lowercase Latin letters, vectors by lowercase boldface Latin letters, matrices by capital Latin letters, and finally sets by capital calligraphic letters. \({\mathbb{R}}^{n}_{+}\) (\({\mathbb{R}}^{n}_{++}\)) is the nonnegative (positive) orthant of \({\mathbb{R}}^{n}\). Further, X is the diagonal matrix whose diagonal elements are the coordinates of the vector x, so \(X=\operatorname{diag}(x)\), and I denotes the identity matrix of appropriate dimension. The vector xs=Xs is the componentwise product (Hadamard product) of the vectors x and s, and for \(\alpha\in \mathbb{R}\) the vector x α denotes the vector whose ith component is \(x^{\alpha}_{i}\). We denote the vector of ones by e. As usual, ∥⋅∥ denotes the 2-norm for vectors and matrices. x min (or x max) denotes the smallest (or largest) value of the components of x. Finally, if g(x)⩾0 is a real valued function of a real nonnegative variable, the notation g(x)=O(x) means that \(g(x)\leqslant\bar{c}x\) for some positive constant \(\bar{c}\).

2 Preliminaries

The monotone linear complementarity problem (LCP) is to find vector pair \((x,s )\in{\mathbb{R}}^{2n}\) that satisfies the following conditions:

figure b

where \(q\in{\mathbb{R}}^{n}\) and M is an n×n matrix supposed positive semidefinite. We denote the feasible set of the problem (P) by

$$\mathcal{F}:= \bigl\{ (x,s )\in{\mathbb{R}}^{2n}_+: s=Mx+q \bigr\} , $$

and its solution set by

$$\mathcal{F^*}:= \bigl\{ \bigl(x^*,s^* \bigr)\in\mathcal{F}: \bigl(x^* \bigr)^Ts^*=0 \bigr\} . $$

To describe the motivation of this paper we need to recall the main ideas underlying the algorithm in [10]. Let (x 0,s 0)>0 be a solution of LCP. We say that (x,s) is an ε-solution of LCP if the ∥Mx+q−s∥⩽ε and also x T s⩽ε.

In the case of an infeasible method we start with choosing arbitrarily (x 0,s 0)>0 such that x 0 s 0=μ 0 e for some (positive) number μ 0. We denote the initial value of the residual as r 0, as

$$ \begin{array}{rcl} r^{0}&=&s^{0}-Mx^{0}-q. \end{array} $$
(2.1)

For any ν with 0<ν⩽1 we consider the perturbed problem (P ν ), defined by

figure c

Note that if ν=1 then (x,s)=(x 0,s 0) yields a strictly feasible solution of (P ν ). We conclude that if ν=1 then (P ν ) satisfies the IPC.

Lemma 2.1

(Lemma 4.1 in [10])

If the original problem (P) is feasible then the perturbed problem (P ν ) satisfies the IPC.

We conclude that if (P) be feasible then (P ν ) satisfies the IPC, and hence its central path exists. This means that the system

$$\begin{aligned} \begin{aligned} s-Mx-q&=\nu r^{0},\quad x\geqslant0,\\ xs&=\mu e,\quad s\geqslant0, \end{aligned} \end{aligned}$$
(2.2)

has a unique solution, for every μ>0. We denote this unique solution as (x(μ,ν),s(μ,ν)). It is the μ-center of the perturbed problem (P ν ). In the sequel the parameters μ and ν always satisfy the relation μ=νμ 0. We measure proximity to the μ-center of the perturbed problems by the quantity δ(x,s;μ) which is defined as follows:

$$\begin{aligned} \delta(x, s;\mu):=\delta(v):=\frac{1}{\sqrt{2}}\bigl\Vert v-v^{-1} \bigr\Vert \quad \mbox{where } v:=\sqrt{\frac{xs}{\mu}}. \end{aligned}$$
(2.3)

At starting of algorithm (in initial iterate) we have (x,s)=(x 0,s 0) and μ=μ 0. We show that if ν=1 and μ=μ 0, then (x,s)=(x 0,s 0) is the μ-center of the perturbed (P ν ). Initially we have δ(x,s;μ)=0. In the sequel we assume that at the start of each iteration, just before the μ-update, δ(x,s;μ) is smaller than or equal to a (small) threshold value τ>0. So this is certainly true at the start of the first iteration.

We are now ready to describe one (main) iteration of our algorithm. Suppose we have (x,s) and μ∈(0,μ 0] such that satisfying the feasibility condition (2.2) for \(\nu=\frac{\mu}{\mu^{0}}\) and x T s⩽(n+δ 2)μ and δ(x,s;μ)⩽τ. We reduce μ to μ +=(1−θ)μ, with θ∈(0,1) and find new iterates (x +,s +) that satisfy (2.2), with μ replaced by μ + and ν by \(\nu^{+}=\frac{\mu^{+}}{\mu^{0}}\), and such that (x +)T s +⩽(n+δ 2)μ + and δ(x +;s +;μ +)⩽τ. Note that ν +=(1−θ)ν. To be more precise, each main iteration consists of a feasibility step and a few centering steps. The feasibility step serves to get iterates (x f,s f) that are strictly feasible for \((P_{\nu^{+}})\), and close to their μ-center (x(μ,ν),s(μ,ν)) such that \(\delta(x^{f},s^{f};\mu^{+})\leqslant\frac{1}{\sqrt{2}}\). Since the (x f,s f) is strictly feasible for \((P_{\nu^{+}})\), we can perform a few centering steps starting at (x f,s f), and obtain iterates (x +,s +) that are feasible for \((P_{\nu^{+}})\) and such that δ(x +,s +;μ +)⩽τ. This process is repeated until the duality gap and the norms of the residual vectors are less than some prescribed accuracy parameter ε.

For the feasibility step in [10] search directions Δ f x and Δ f s are defined by the following system:

$$\begin{aligned} M\varDelta^{f}x-\varDelta^{f}s =&\theta\nu r^{0}, \end{aligned}$$
(2.4)
$$\begin{aligned} x\varDelta^{f}s+s\varDelta^{f}x =&\mu e-xs. \end{aligned}$$
(2.5)

Since matrix M is positive semidefinite, the system (2.4)–(2.5) uniquely defines (Δ f x,Δ f s) for any x>0 and s>0. After the feasibility step the iterates given by

$$\begin{aligned} x^{f} =&x+\varDelta^{f}x,\\ s^{f} =&s+\varDelta^{f}s. \end{aligned}$$

We conclude that after the feasibility step the iterates satisfy the affine equation (2.2) with ν=ν +. In a centering step the search directions (Δx,Δs) are the usual primal–dual Newton directions, (uniquely) defined by

$$\begin{aligned} M\varDelta x-\varDelta s =&0,\\ x\varDelta s+s\varDelta x =&\mu e-xs. \end{aligned}$$

Denoting the iterates after a centering step as (x +,s +), we recall from [10] the following results.

Lemma 2.2

(Lemma 3.5 in [10])

If δ<1 then x +,s + are positive and

$$\begin{aligned} \delta\bigl(x^{+},s^{+};\mu\bigr)\leqslant \frac{\delta^{2}}{\sqrt{2(1-\delta^{2}})}. \end{aligned}$$

Corollary 2.1

(Corollary 3.6 in [10])

If \(\delta=\delta(x,s;\mu)\leqslant\frac{1}{\sqrt{2}}\) then

$$\delta\bigl(x^{+},s^{+};\mu\bigr)\leqslant\delta^{2}. $$

After the feasibility step we perform centering steps in order to get iterates (x +,s +) that satisfy (x +)T s +⩽(n+δ 2)μ + and δ(x +,s +;μ +)⩽τ, where τ⩾0. Assuming \(\delta(x^{f},s^{f};\mu^{+})\leqslant\frac{1}{\sqrt{2}}\), after k centering steps we will have iterates (x +,s +) that are still feasible for \((P_{\nu^{+}})\) and that satisfy

$$\begin{aligned} \delta\bigl(x^{+}, s^{+};\mu^{+}\bigr)\leqslant \biggl(\frac{1}{\sqrt{2}}\biggr)^{2^{k}}. \end{aligned}$$

Therefore, δ(x +,s +;μ +)⩽τ will hold if k satisfies

$$\begin{aligned} \biggl(\frac{1}{\sqrt{2}}\biggr)^{2^{k}}\leqslant\tau. \end{aligned}$$

From this one easily deduce that δ(x +,s +;μ +)⩽τ will hold after at most

$$\begin{aligned} \bigg\lceil \log_{2} \biggl(\log_{2}\frac{1}{\tau^{2}}\biggr)\bigg\rceil , \end{aligned}$$

centering steps.

3 Adaptive Infeasible Interior-Point Algorithm

In this paper, we use another definition for the feasibility step by replacing Eq. (2.5) by the equation

$$\begin{aligned} x\varDelta^{f}s+s\varDelta^{f}x =&\mu^{+}e-xs. \end{aligned}$$
(3.1)

Now let us replace (2.5) by (3.1) which implies the following system:

$$\begin{aligned} M\varDelta^{f}x-\varDelta^{f}s =&\theta \nu r^{0}, \end{aligned}$$
(3.2)
$$\begin{aligned} x\varDelta^{f}s+s\varDelta^{f}x =&\mu^{+} e-xs. \end{aligned}$$
(3.3)

3.1 Analysis of the Adaptive Feasibility Step

The important and hard part of the analysis is to prove quadratic convergence property of feasibility step. In other words we should guarantee that (x f,s f) is strictly feasible and moreover belong to the region of quadratic convergence of their μ +-center (x(μ +,ν +),s(μ +,ν +)). However, we must show \(\delta(x^{f},s^{f};\mu^{+})\leqslant\frac{1}{\sqrt{2}}\) and proving this, is the crucial part in the analysis of the algorithm. The main goal of this paper is to investigate how large θ can be so that it guarantees that after the feasibility step the iterates x f and s f are nonnegative and moreover \(\delta(x^{f}, s^{f};\mu^{+})\leqslant\frac{1}{\sqrt{2}}\), where μ +=(1−θ)μ. The same as proposed algorithm in [10] after the feasibility step we perform centering steps in order to get iterates (x +,s +) that satisfy (x +)T s +⩽(n+δ 2)μ + and δ(x +,s +;μ +)⩽τ, where τ⩾0. A more formal description of the algorithm is given in Fig. 1. Note that after each iteration the residual and the value of nμ are reduced by a factor 1−θ. The algorithm stops if the norm of the residual and the value of nμ are less than the accuracy parameter ε.

Fig. 1
figure 1

Adaptive infeasible full-Newton-step algorithm

Full size image

In sequel we present some definitions and Lemmas to show that (x f,s f) is strictly feasible.

Defining

$$\begin{aligned} v=\sqrt{\frac{xs}{\mu}},\qquad d=\sqrt{\frac{x}{s}},\qquad d^{f}_{x}=\frac{d^{-1}\varDelta^{f}x}{\sqrt{\mu^{+}}},\qquad d^{f}_{s}=\frac{d\varDelta^{f}s}{\sqrt{\mu^{+}}}. \end{aligned}$$
(3.4)

Now by using (3.1) and the notations (3.4) we may write

$$\begin{aligned} x^{f}s^{f}=xs+\bigl(x\varDelta^{f}s+s \varDelta^{f}x\bigr)+ \varDelta^{f}x\varDelta^{f}s =&\mu^{+}e+\varDelta^{f}x\varDelta^{f}s \\ =&\mu^{+}\bigl(e+d^{f}_{x}d^{f}_{s} \bigr). \end{aligned}$$
(3.5)

Lemma 3.1

(Lemma 5.1 in [10])

The new iterates are certainly strictly feasible if

$$e+d^{f}_{x}d^{f}_{s}>0. $$

Corollary 3.1

(Corollary 5.2 in [10])

The iterates (x f,s f) are certainly strictly feasible if

$$\bigl\Vert d^{f}_{x}d^{f}_{s} \bigr\Vert _{\infty}<1. $$

By using the definition of norms one has the following inequalities:

$$\begin{aligned} \bigl\Vert d^{f}_{x}d^{f}_{s} \bigr\Vert ^{2} \leqslant & \bigl(\bigl\Vert d^{f}_{x} \bigr\Vert \bigl\Vert d^{f}_{s} \bigr\Vert \bigr)^{2} \leqslant\frac{1}{4} \bigl(\bigl\Vert d^{f}_{x} \bigr\Vert ^{2}+\bigl\Vert d^{f}_{s} \bigr\Vert ^{2} \bigr)^{2} , \end{aligned}$$
(3.6)
$$\begin{aligned} \bigl\Vert {d^{f}_{x}d^{f}_{s}} \bigr\Vert _{\infty} \leqslant& \bigl\Vert d^{f}_{x} \bigr\Vert \bigl\Vert d^{f}_{s} \bigr\Vert \leqslant \frac{1}{2} \bigl(\bigl\Vert d^{f}_{x} \bigr\Vert ^{2}+\bigl\Vert d^{f}_{s} \bigr\Vert ^{2} \bigr) . \end{aligned}$$
(3.7)

To simply the presentation we will denote δ(x,s;μ) below simply as δ. Recall that we already assumed that in feasibility step one has δ⩽τ.

Recall from definition (2.3) that

$$\begin{aligned} \delta\bigl(x^{f}, s^{f};\mu^{+}\bigr)= \frac{1}{\sqrt{2}}\bigl\Vert v^{f}-\bigl(v^{f} \bigr)^{-1} \bigr\Vert , \end{aligned}$$

where \(v^{f}=\sqrt{\frac{x^{f}s^{f}}{\mu^{+}}}\). Furthermore, from (3.5) we have

$$\begin{aligned} \bigl(v^{f}\bigr)^{2}=\frac{x^{f}s^{f}}{\mu^{+}}= \frac{\mu ^{+}(e+d^{f}_{x}d^{f}_{s})}{\mu^{+}}=e+d^{f}_{x}d^{f}_{s}. \end{aligned}$$

Therefore

$$\begin{aligned} v^{f}=\sqrt{e+d^{f}_{x}d^{f}_{s}}, \end{aligned}$$

which implies that

$$\begin{aligned} 2\delta\bigl(v^{f}\bigr)^{2} =& \bigl\Vert \bigl(v^{f}\bigr)^{-1}-v^{f} \bigr\Vert ^{2}=\bigl\Vert \bigl(v^{f}\bigr)^{-1} \bigl(e- \bigl(v^{f}\bigr)^{2} \bigr) \bigr\Vert ^{2} \\ =&\biggl\Vert \frac{d^{f}_{x}d^{f}_{s}}{\sqrt{e+d^{f}_{x}d^{f}_{s}}} \biggr\Vert ^{2} \leqslant \frac{\Vert {d^{f}_{x}d^{f}_{s}} \Vert ^{2}}{1-\Vert {d^{f}_{x}d^{f}_{s}} \Vert _{\infty}}. \end{aligned}$$

This implies that we have \(\delta(v^{f})\leqslant\frac{1}{\sqrt{2}}\) if and only if

$$\begin{aligned} 2\delta\bigl(v^{f}\bigr)^{2}\leqslant \frac{\Vert {d^{f}_{x}d^{f}_{s}} \Vert ^{2}}{1-\Vert {d^{f}_{x}d^{f}_{s}} \Vert _{\infty}} \leqslant1. \end{aligned}$$
(3.8)

Substituting (3.6) and (3.7) in (3.8) we obtain the condition

$$\begin{aligned} \frac{\frac{1}{4} (\Vert d^{f}_{x} \Vert ^{2}+\Vert d^{f}_{s} \Vert ^{2} )^{2}}{1-\frac{1}{2} (\Vert d^{f}_{x} \Vert ^{2}+\Vert d^{f}_{s} \Vert ^{2} )}\leqslant1. \end{aligned}$$

By some elementary calculations, we find that (3.8) holds if

$$\begin{aligned} \bigl\Vert d^{f}_{x} \bigr\Vert ^{2}+\bigl\Vert d^{f}_{s} \bigr\Vert ^{2}\leqslant \sqrt{5}-1\approx1.236. \end{aligned}$$
(3.9)

By using (3.7), (3.9), and Corollary 3.1 we conclude that the iterates after the feasibility step are feasible. In other words, the inequality (3.9) implies that after the feasibility step (x f,s f) is strictly feasible and lies in the quadratic convergence neighborhood with respect to the μ +-center of \((P_{v^{+}})\).

In the following we proceed by calculating an upper bound for \(\Vert d^{f}_{x} \Vert ^{2}+\Vert d^{f}_{s} \Vert ^{2}\).

3.2 An Upper Bound for \(\Vert d^{f}_{x} \Vert ^{2}+\Vert d^{f}_{s} \Vert ^{2}\)

One may easily check that the system (3.2)–(3.3), which defines the search direction Δ f x and Δ f s, can be expressed in terms of the scaled search direction \(d^{f}_{x}\) and \(d^{f}_{s}\) as follows:

$$\begin{aligned} MS^{-1}Xd^{f}_{x}-d^{f}_{s} =&\frac{\theta}{\sqrt{1-\theta}}\nu vs^{-1}r^{0}, \end{aligned}$$
(3.10)
$$\begin{aligned} d_{x}^{f}+d_{s}^{f} =&\sqrt{1-\theta}v^{-1}-\frac{v}{\sqrt{1-\theta}}, \end{aligned}$$
(3.11)

where \(X=\operatorname{diag}(x),S=\operatorname{diag}(s)\).

Lemma 3.2

(Lemma 5.5 in [10])

Let x>0 and s>0 be two n-dimensional vectors, and let \(M\in \mathbb{R}^{n\times n}\) be a positive semidefinite matrix. Then the solution (u,z) of the linear system

$$\begin{aligned} MS^{-1}Xu-z =&\tilde{a} \\ u+z =&\tilde{b} \end{aligned}$$

satisfies the following relations:

$$\begin{aligned} &Du=(I+DMD)^{-1}(a+b),\qquad Dz=b-Du, \end{aligned}$$
(3.12)
$$\begin{aligned} &\Vert Du \Vert \leqslant \Vert a+b \Vert , \end{aligned}$$
(3.13)
$$\begin{aligned} &\Vert Du \Vert ^{2}+\Vert Dz \Vert ^{2}\leqslant \Vert b \Vert ^{2}+2\Vert a+b \Vert \Vert a \Vert , \end{aligned}$$
(3.14)

where \(D=(S^{-1}X)^{\frac{1}{2}},b=D\tilde{b}\) and \(a=D\tilde{a}\).

Lemma 3.3

(Lemma 5.6 in [10])

Let δ=δ(ν) be given by (2.3). Then

$$\begin{aligned} \frac{1}{q(\delta)}\leqslant v_{i} \leqslant q(\delta), \end{aligned}$$
(3.15)

where

$$\begin{aligned} q(\delta)=\frac{\sqrt{2}}{2}\delta+\sqrt{\frac{1}{2}\delta^{2}+1}. \end{aligned}$$
(3.16)

We are now ready to find an upper bound for \(\Vert d^{f}_{x} \Vert ^{2}+\Vert d^{f}_{s} \Vert ^{2}\). To this end we first apply Lemma 3.2 with \(u=d^{f}_{x}\),\(z=d^{f}_{s}\), \(a=\frac{\theta}{\sqrt{1-\theta}}\nu Dv s^{-1}r^{0}\) and \(b=D(\sqrt{1-\theta}v^{-1}-\frac{v}{\sqrt{1-\theta}})\), which implies that

$$\begin{aligned} &\bigl\Vert Dd^{f}_{x} \bigr\Vert ^{2}+\bigl\Vert Dd^{f}_{s} \bigr\Vert ^{2} \\ &\quad\leqslant\biggl\Vert D \biggl(\sqrt {1-\theta}v^{-1}- \frac{v}{\sqrt{1-\theta}} \biggr) \biggr\Vert ^{2} \\ &\qquad{}+2\biggl\Vert \frac{\theta}{\sqrt{1-\theta}}\nu D vs^{-1}r^{0} +D \biggl(\sqrt{1-\theta}v^{-1}-\frac{v}{\sqrt{1-\theta}} \biggr) \biggr\Vert \biggl\Vert \frac{\theta}{\sqrt{1-\theta}}\nu D vs^{-1}r^{0} \biggr\Vert . \end{aligned}$$
(3.17)

By elementary properties of norms we have

$$\begin{aligned} \bigl\Vert Dd^{f}_{x} \bigr\Vert \leqslant \Vert D \Vert \bigl\Vert d^{f}_{x} \bigr\Vert ,\qquad\bigl\Vert Dd^{f}_{s} \bigr\Vert \leqslant \Vert D \Vert \bigl\Vert d^{f}_{s} \bigr\Vert , \end{aligned}$$

and

$$\begin{aligned} \biggl\Vert \frac{\theta}{\sqrt{1-\theta}}\nu D v s^{-1}r^{0} \biggr\Vert \leqslant&\Vert D \Vert \biggl\Vert \frac{\theta}{\sqrt{1-\theta}}\nu v s^{-1}r^{0} \biggr\Vert ,\\ \biggl\Vert D \biggl(\sqrt{1-\theta}v^{-1}-\frac{v}{\sqrt{1-\theta}} \biggr) \biggr\Vert \leqslant& \Vert D \Vert \biggl\Vert \sqrt{1-\theta}v^{-1}-\frac{v}{\sqrt{1-\theta}} \biggr\Vert . \end{aligned}$$

Substituting these bounds in (3.17) we obtain the following weaker condition:

$$\begin{aligned} &\bigl\Vert d^{f}_{x} \bigr\Vert ^{2}+\bigl\Vert d^{f}_{s} \bigr\Vert ^{2} \\ &\quad\leqslant\biggl\Vert \sqrt{1-\theta}v^{-1}-\frac{v}{\sqrt {1-\theta}} \biggr\Vert ^{2} \\ &\qquad{}+2 \biggl(\biggl\Vert \frac{\theta}{\sqrt{1-\theta}}\nu vs^{-1}r^{0} \biggr\Vert +\biggl\Vert \sqrt{1-\theta}v^{-1}-\frac{v}{\sqrt{1-\theta}} \biggr\Vert \biggr) \biggl\Vert \frac{\theta}{\sqrt{1-\theta}}\nu v s^{-1}r^{0} \biggr\Vert . \end{aligned}$$
(3.18)

Since the term \(\sqrt{1-\theta}v^{-1}-\frac{v}{\sqrt{1-\theta}}\) equals with \(\frac{1}{\sqrt{1-\theta}} ( v^{-1}-v-\theta v^{-1} )\) and by using (2.3), Lemma 3.3 and by elementary properties of norms we have

$$\begin{aligned} &\bigl\Vert d^{f}_{x} \bigr\Vert ^{2}+\bigl\Vert d^{f}_{s} \bigr\Vert ^{2} \\ &\quad\leqslant\frac{1}{1-\theta} \bigl(\bigl(\sqrt{2}\delta+\theta q(\delta) \bigr)^{2}+2 \bigl(\bigl\Vert \theta\nu vs^{-1}r^{0} \bigr\Vert +\sqrt{2}\delta+\theta q(\delta) \bigr)\bigl\Vert \theta\nu vs^{-1}r^{0} \bigr\Vert \bigr). \end{aligned}$$
(3.19)

In order to obtain a bound for ∥θνvs −1 r 0∥ we write, using \(v=\frac{\mu}{\mu^{0}}\) and \(v=\sqrt{\frac{xs}{\mu}}\),

$$\begin{aligned} \bigl\Vert \theta\nu v s^{-1}r^{0} \bigr\Vert =& \theta\nu\ \bigl\Vert v s^{-1}r^{0} \bigr\Vert =\theta \frac{\sqrt{\mu}}{\mu^{0}}\biggl\Vert \sqrt{\frac{x}{s}}r^{0} \biggr\Vert \leqslant\theta\frac{\sqrt{\mu}}{\mu^{0}}\biggl\Vert \sqrt{\frac{x}{s}}r^{0}\biggr\Vert _{1} \\ =&\frac{\theta}{\mu^{0}}\biggl\Vert \sqrt{\frac{\mu}{xs}}xr^{0}\biggr\Vert _{1} \leqslant \frac{\theta}{\mu^{0}v_{\min}}\bigl\Vert xr^{0} \bigr\Vert _{1} \\ \leqslant& \frac{\theta}{\mu^{0}v_{\min}}\bigl\Vert \bigl(S^{0} \bigr)^{-1}r^{0} \bigr\Vert _{\infty} \bigl\Vert s^{0} \bigr\Vert _{\infty} \Vert x \Vert _{1}. \end{aligned}$$
(3.20)

To proceed we have to specify our initial iterates (x 0,s 0). We assume that ρ p and ρ d are such that

$$\begin{aligned} \bigl\Vert x^{*} \bigr\Vert _{\infty}\leqslant \rho_{p},\quad\max\bigl\{ \bigl\Vert s^{*} \bigr\Vert _{\infty}, \rho_{p}\Vert Me \Vert _{\infty},\Vert q \Vert _{\infty}\bigr\} \leqslant\rho_{d}, \end{aligned}$$
(3.21)

for some \((x^{*},s^{*})\in\mathcal{F^{*}}\), and as usual we start the algorithm with

$$\begin{aligned} x^{0}=\rho_{p}e,\qquad s^{0}=\rho_{d}e ,\qquad\mu^{0}=\rho_{p}\rho_{d}. \end{aligned}$$
(3.22)

For such starting points we have clearly

$$\begin{aligned} \bigl\Vert \bigl(S^{0}\bigr)^{-1}r^{0} \bigr\Vert _{\infty }\leqslant 1+\frac{\rho_{p}}{\rho_{d}}\Vert Me \Vert _{\infty}+ \frac{1}{\rho_{d}}\Vert q \Vert _{\infty} \leqslant3. \end{aligned}$$
(3.23)

By using (3.15) and substituting (3.22) and (3.23) into (3.20) we obtain

$$\begin{aligned} \bigl\Vert \theta\nu v s^{-1}r^{0} \bigr\Vert \leqslant \frac{3\theta q(\delta)}{\rho_{p}}{\Vert x \Vert }_{1}. \end{aligned}$$
(3.24)

Using (3.24) in (3.19) we get

$$\begin{aligned} &\bigl\Vert d^{f}_{x} \bigr\Vert ^{2}+\bigl\Vert d^{f}_{s} \bigr\Vert ^{2} \\ &\quad\leqslant \frac{1}{1-\theta} \biggl( \bigl(\sqrt{2}\delta+\theta q(\delta) \bigr)^{2}+2 \biggl(\frac{3\theta q(\delta)}{\rho_{p}}{\Vert x \Vert }_{1}+\sqrt{2}\delta +\theta q(\delta) \biggr)\frac{3\theta q(\delta)}{\rho_{p}}{\Vert x \Vert }_{1} \biggr). \end{aligned}$$
(3.25)

Recall that (x,s) is feasible for (P ν ) and δ(x,s;μ)⩽τ; i.e., this iterate is close to the μ-center of (P ν ). Based on this information, we present the following lemmas to estimate an upper bound for ∥x∥1.

Lemma 3.4

(Lemma 5.7 in [10])

Let (x,s) be feasible for the perturbed problem (P ν ) and (x 0,s 0) as defined in (3.22). Then for any (x ∗,s ∗)∈F ∗, we have

$$\begin{aligned} \nu \bigl( \bigl(s^{0}\bigr)^{T}x+\bigl(x^{0}\bigr)^{T}s \bigr) \leqslant& \nu^{2}\bigl(x^{0}\bigr)^{T}s^{0}+x^{T}s+\nu(1-\nu) \bigl(\bigl(s^{0}\bigr)^{T}x^{*}+\bigl(x^{0} \bigr)^{T}s^{*} \bigr)\\ &{}-(1-\nu) \bigl(s^{T}x^{*}+x^{T}s^{*}\bigr). \end{aligned}$$

Lemma 3.5

(Lemma 5.8 in [10])

Let (x,s) be feasible for the perturbed problem (P ν ) and δ(v) is defined in (2.3) and (x 0,s 0) as defined in (3.22). Then we have

$$\begin{aligned} \Vert x \Vert _{1} \leqslant& \bigl(2+q(\delta)^{2} \bigr)n\rho_{p}, \end{aligned}$$
(3.26)
$$\begin{aligned} \Vert s \Vert _{1} \leqslant& \bigl( 2+q(\delta)^{2} \bigr)n\rho_{d}. \end{aligned}$$
(3.27)

By substituting (3.26) into (3.25) we obtain

$$\begin{aligned} &\bigl\Vert d^{f}_{x} \bigr\Vert ^{2}+\bigl\Vert d^{f}_{s}\bigr\Vert ^{2} \\ &\quad\leqslant \frac{1}{1-\theta} \bigl( \bigl(\sqrt{2}\delta+\theta q(\delta) \bigr)^{2} \\ &\qquad{}+2 \bigl({3n\theta q(\delta)} \bigl( q(\delta)^{2}+2 \bigr)+\sqrt{2} \delta+\theta q(\delta) \bigr){3n\theta q(\delta)} \bigl( q(\delta)^{2}+2\bigr) \bigr). \end{aligned}$$
(3.28)

3.3 Value for θ

We have found that \(\delta(v^{f})\leqslant\frac{1}{\sqrt{2}}\) holds if the inequality (3.9) is satisfied. Then by (3.28), inequality (3.9) holds if

$$\begin{aligned} &\bigl(\sqrt{2}\delta+\theta q(\delta) \bigr)^{2} +2 \bigl({3n\theta q(\delta)} \bigl( q(\delta)^{2}+2 \bigr)+\sqrt{2}\delta+\theta q(\delta) \bigr){3n\theta q(\delta)} \bigl( q(\delta)^{2}+2 \bigr) \\ &\quad\leqslant1.236(1-\theta). \end{aligned}$$
(3.29)

With a value of θ that satisfies (3.29), we are sure that when starting with δ(x,s;μ)=δ⩽τ, after the feasibility step with parameter value μ +=(1−θ)μ we have \(\delta(x^{f}, s^{f};\mu^{+})\leqslant\frac{1}{\sqrt{2}}\). Also we set \(\tau=\frac{1}{8}\).

If δ=0, the above expression in (3.29) reduces to

$$\begin{aligned} \bigl(162 n^{2}+ 18n+1\bigr)\theta^{2}+1.236\theta -1.236 \leqslant0. \end{aligned}$$

One may easily verify that the above inequality is satisfied to \(\theta=\frac{1}{13n}\).

If \(\delta=\frac{1}{8}\) we have

$$\begin{aligned} \bigl(217.56 n^{2}+ 22.74n+1.19\bigr)\theta^{2}+(3.76n+1.62) \theta-1.206\leqslant0. \end{aligned}$$

One may easily verify that the above inequality is satisfied to \(\theta =\frac{1}{17n}\).

Hence, when using adaptive updates the value of θ varies from iteration to iteration but it always lies between the above two values. It is clear that under the assumption that there exists an optimal solution with \((x^{*},s^{*} )\in\mathcal{F}^{*}\) such that ∥x ∗∥∞⩽ρ p ,∥x ∗∥∞⩽ρ d and \(\theta\in (\frac{1}{17n},\frac{1}{13n} )\), the algorithm convergent to the ε-solution. One might ask what happens if the assumption is not satisfied. In that case, during the course of the algorithm it may happen that after some main steps the proximity measure δ (after the feasibility step) exceeds \(\frac{1}{\sqrt{2}}\), because otherwise there is no reason why the algorithm would not generate an ε-solution. So if this happens it tell us that either (P) does not have an optimal solution in \(\mathcal{F}^{*}\) or the values of ρ p and ρ d have been too small. In the latter case one might run the algorithm once more with some larger ρ p and ρ d [7, 10, 18].

4 Numerical Results

In this section, we present numerical results under the MATLAB environment. We consider the following examples in [12, 19].

Example 4.1

$$\begin{aligned} M=\left [\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 2 & 2 & 1 \\ \end{array} \right ],\qquad q=\left [\begin{array}{c} -1 \\ -1\\ -1\\ \end{array} \right ]. \end{aligned}$$

Example 4.2

$$\begin{aligned} M=\left [\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 2 & 1& 1 & 1\\ 1 & 2 & 0 & 1 \\ 1 & 0 & 1 & 2 \\ -1 & -1 & -2 & 0 \\ \end{array} \right ],\qquad q=\left [\begin{array}{c} -8 \\ -6\\ -4\\ 3 \\ \end{array} \right ]. \end{aligned}$$

Example 4.3

$$\begin{aligned} M =&\left [\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0.0368& 0.0188& 0.0920& 0.0211& 0.0332& 0.0162\\ 0.0188 & 0.3930 & 0.0634 & 0.0176 & 0.3000& 0.0248\\ 0.0920 & 0.0634 & 0.4293 & 0.0617 & 0.1355& 0.1124\\ 0.0211 & 0.0176 & 0.0617 & 0.0203& 0.0239& 0.0107\\ 0.0332 & 0.0300 & 0.1355 & 0.0239& 0.0513&0.0480\\ 0.0162 & 0.0248 & 0.1124 & 0.0107& 0.0480 & 0.0824\\ \end{array} \right ],\\ q =&\left [\begin{array}{c} -0.1630\\ 0.2820\\ -0.4500\\ 0.3560\\ -0.2420\\ 0.2489\\ \end{array} \right ]. \end{aligned}$$

We solve the above examples using the classical interior-point algorithm presented in [10] and the algorithm in Fig. 1. We have to note that the starting point for these problems has been chosen based on (3.29), and the accuracy parameter ε is set to 10−3. In the classical algorithm we suppose the value of barrier parameter is constant. However, in the adaptive algorithm presented in Fig. 1 not only the value of barrier parameter is not constant but also in each iteration of the algorithm we use the largest possible barrier parameter value θ which lies between the two values \(\frac{1}{17n}\) and \(\frac{1}{13n}\), this makes the algorithm faster convergent for problems having a strictly complementarity solution. Table 1 shows the number of iterations to obtain ε-solutions of the three above examples.

Table 1 The number of iterations for Examples 4.1, 4.2 and 4.3
Full size table

5 Concluding Remarks

In this paper we extended adaptive infeasible proposed algorithm in [9] for LO to LCP. To this end we improved analysis of suggested algorithm in [10]. In each iteration of the algorithm we use the largest possible barrier parameter value θ instead a constant value. The feasibility step differs slightly in this algorithm, where different right-hand sides were used in Eq. (3.3). The proposed algorithm has better results and converges faster.