1 Introduction

We consider the equality constrained optimization problem

$$\begin{aligned} &\text{minimize} \qquad f(x), \quad x\in\mathbb{R}^{n}, \end{aligned}$$
(1.1)
$$\begin{aligned} &\text{subject to}\qquad h_{i}(x)=0,\quad i=1,\cdots ,m, \end{aligned}$$
(1.2)

where \(f:\mathbb{R}^{n}\to\mathbb{R}\) and \(h_{i}:\mathbb{R}^{n}\to \mathbb{R}\) (i=1,⋯,m) are continuously differentiable, and the constraints gradients are linearly independent. For convenience, throughout this paper the following notation is used:

$$\begin{aligned} c(x) =& \bigl(h_{1}(x),\cdots ,h_{m}(x) \bigr)^{T}, \end{aligned}$$
(1.3)
$$\begin{aligned} A(x) =&J_{c}(x)^{T}= \bigl(\nabla h_{1}(x), \cdots ,\nabla h_{m}(x) \bigr), \end{aligned}$$
(1.4)
$$\begin{aligned} g(x) =&\nabla f(x). \end{aligned}$$
(1.5)

We also use c k for c(x k ), A k for A(x k ), g k for g(x k ), etc.

The Powell–Yuan trust-region algorithm [11] is an iterative procedure to solve (1.1)–(1.2), which generates a sequence of points {x k } in the following way. At the beginning of the kth iteration, \(x_{k}\in\mathbb{R}^{n}\), Δ k >0 and \(B_{k}\in\mathbb{R}^{n\times n}\) symmetric are available. If x k does not satisfy the Kuhn–Tucker conditions, a trial step s k is computed by solving the CDT subproblem (see Celis, Dennis and Tapia [2]):

$$\begin{aligned} &\min_{d\in\mathbb{R}^{n}}\, \phi_{k}(d)\equiv g_{k}^{T}d+ \frac {1}{2}d^{T}B_{k}d, \end{aligned}$$
(1.6)
$$\begin{aligned} &\mathrm{s.t.}\quad \big\| c_{k}+A_{k}^{T}d \big\| _{2}\leqslant \xi_{k}, \end{aligned}$$
(1.7)
$$\begin{aligned} &\phantom{\mathrm{s.t.}\quad} \|d\|_{2}\leqslant \varDelta_{k}, \end{aligned}$$
(1.8)

where ξ k is any number satisfying the inequalities

$$ \min_{\|d\|_{2}\leqslant b_{1}\varDelta_{k}}\big\| c_{k}+A_{k}^{T}d \big\| _{2}\leqslant \xi _{k}\leqslant \min_{\|d\|_{2}\leqslant b_{2}\varDelta_{k}} \big\| c_{k}+A_{k}^{T}d\big\| _{2}, $$
(1.9)

and b 1 and b 2 are two given constants with 0<b 2⩽b 1<1. The merit function is Fletcher’s differentiable function:

$$ \psi_{k}(x)=f(x)-\lambda(x)^{T}c(x)+\mu_{k} \big\| c(x)\big\| _{2}^{2}, $$
(1.10)

where μ k >0 is a penalty parameter and λ(x) is the minimum norm solution of

$$ \min_{\lambda\in\mathbb{R}^{m}}\big\| g(x)-A(x)\lambda\big\| _{2}. $$
(1.11)

The predicted change D k in ψ k (x) is defined by

$$\begin{aligned} D_{k} =& (g_{k}-A_{k}\lambda_{k} )^{T}s_{k}+\frac {1}{2}s_{k}^{T}B_{k} \hat{s}_{k}- \bigl[\lambda(x_{k}+s_{k})-\lambda _{k} \bigr]^{T}\biggl(c_{k}+\frac{1}{2}A_{k}^{T}s_{k} \biggr) \\ &{}+\mu_{k} \bigl(\big\| c_{k}+A_{k}^{T}s_{k} \big\| _{2}^{2}-\|c_{k}\| _{2}^{2} \bigr), \end{aligned}$$
(1.12)

where μ k is chosen so that D k <0 and where \(\hat{s}_{k}\) is the orthogonal projection of s k to the null space of \(A_{k}^{T}\), namely

$$ \hat{s}_{k}=P_{k}s_{k},\quad\mathrm{with}\ P_{k}=I_{n}-A_{k}A_{k}^{+}. $$
(1.13)

From the ratio

$$ \rho_{k}=\frac{\psi_{k}(x_{k}+s_{k})-\psi_{k}(x_{k})}{D_{k}}, $$
(1.14)

the next iterate x k+1 is obtained by the formula

$$ x_{k+1}=\left \{ \begin{array}{l@{\quad}l} x_{k}+s_{k},& \text{if}\ \rho_{k}>0,\\ x_{k}, &\text{otherwise}. \end{array} \right . $$
(1.15)

Further, the trust-region radius Δ k+1 for the next iteration is given by the rule

$$ \varDelta_{k+1}=\left \{ \begin{array}{l@{\quad}l} \max \{\varDelta_{k},4\|s_{k}\|_{2} \},& \text{if}\ \rho _{k}>0.9,\\ \varDelta_{k}, & \text{if}\ 0.1\leqslant \rho_{k}\leqslant 0.9,\\ \min \{\frac{\varDelta_{k}}{4},\frac{\|s_{k}\|_{2}}{2} \} ,&\text{if}\ \rho_{k}<0.1. \end{array} \right . $$
(1.16)

Finally, a symmetric matrix B k+1 is obtained and the process is repeated with k:=k+1.

We summarize the above trust-region algorithm as follows:

Algorithm 1.1

(Powell–Yuan Trust-Region Algorithm)

  1. Step 0

    Given \(x_{1}\in\mathbb{R}^{n}\), Δ 1>0, \(B_{1}\in \mathbb{R}^{n\times n}\) symmetric, ε s >0, μ 1>0 and 0<b 2⩽b 1<1, set k:=1.

  2. Step 1

    If ∥c k ∥2+∥g k −A k λ k ∥2⩽ε s , then stop. Otherwise, compute ξ k satisfying (1.9) and solve the CDT subproblem (1.6)–(1.8) to obtain a trial step s k .

  3. Step 2

    Compute D k by (1.12). If the inequality

    $$ D_{k}\leqslant \frac{1}{2}\mu_{k} \bigl( \big\| c_{k}+A_{k}^{T}s_{k} \big\| _{2}^{2}-\| c_{k}\|_{2}^{2} \bigr) $$
    (1.17)

    fails, then increase μ k to the value

    $$ \mu_{k}^{\mathrm{new}}=2\mu_{k}^{\mathrm{old}}+\max \biggl\{ 0,\frac{2D_{k}^{\mathrm{old}}}{\| c_{k}\|_{2}^{2}-\|c_{k}+A_{k}^{T}s_{k}\|_{2}^{2}} \biggr\} $$
    (1.18)

    which ensures that the new value of expression (1.12) satisfies condition (1.17).

  4. Step 3

    Compute ρ k by (1.14);

    Set x k+1 by (1.15);

    Set Δ k+1 by (1.16).

  5. Step 4

    Generate B k+1 symmetric, set μ k+1:=μ k , k:=k+1 and go to Step 1.

To solve the CDT subproblem (1.6)–(1.8) in Step 1, some iterative algorithms have been presented. For example, under the assumption that B k is positive definite, two different algorithms have been proposed by Yuan [16] and Zhang [17], respectively; while for a general symmetric matrix B k , an algorithm has been proposed by Li and Yuan [9]. However, since these algorithms require repeated matrix factorizations in each iteration, it could be very costly to solve the CDT subproblem (1.6)–(1.8), mainly for problems with a large number of variables and constraints.

Motivated by the subspace trust-region method for unconstrained optimization proposed by Wang and Yuan [14], in this paper we explore the subspace properties of the CDT subproblem when the matrices B k are updated by quasi-Newton formulas. With an analysis totally analog to that in Wang and Yuan [14], it is found that the trial step s k defined by the CDT subproblem (1.6)–(1.8) is always in the subspace G k spanned by

$$\bigcup_{i=1}^{k} \bigl\{ \nabla h_{1}(x_{i}),\cdots ,\nabla h_{m}(x_{i}),g_{i} \bigr\} . $$

Therefore, it is equivalent to solving the subproblem within this subspace. Based on this observation, we can solve a smaller CDT subproblem in early iterations of the algorithm, reducing the computational effort for problems where the dimension of the subspace G k remains far smaller than the number of variables n.

This work is organized as follows. The equivalence between the CDT subproblem and that in the subspace is proved in the next section. In Sect. 3, a subspace version of the Powell–Yuan algorithm is proposed. The global convergence analysis is given in Sect. 4. Finally, preliminary numerical results on problems in CUTEr collection are reported in Sect. 5.

2 Subspace Properties

In this section, we shall study subspace properties of the trial step s k at the kth iteration, which is assumed to be a solution of the CDT subproblem (1.6)–(1.8). All the results here are developed corresponding to those presented in Sect. 2 of Wang and Yuan [14].

Lemma 2.1

Let \(s_{k}\in\mathbb{R}^{n}\) be a solution of (1.6)–(1.8), and assume that

$$\xi_{k}>\min_{\|d\|_{2}\leqslant \varDelta_{k}} \big\| c_{k}+A_{k}^{T}d \big\| _{2}. $$

Then, there exist non-negative constants α k and β k such that

$$ \bigl(B_{k}+\alpha_{k}I_{n}+ \beta_{k}A_{k}A_{k}^{T} \bigr)s_{k}=- (g_{k}+\beta_{k}A_{k}c_{k} ), $$
(2.1)

where α k and β k satisfy the complementarity conditions

$$ \alpha_{k} \bigl[\varDelta_{k}-\|s_{k}\|_{2} \bigr]=0, $$
(2.2)
$$ \beta_{k} \bigl[\xi_{k}-\big\| A_{k}^{T}s_{k}+c_{k} \big\| _{2} \bigr]=0. $$
(2.3)

Proof

See Theorem 2.1 in Yuan [15]. □

Lemma 2.2

Let S k be an r (1⩽r⩽n) dimensional subspace in \(\mathbb {R}^{n}\), and \(Z_{k}\in\mathbb{R}^{n\times r}\) is an orthonormal basis matrix of S k , namely

$$ S_{k}=\mathrm{span} \{Z_{k} \},\qquad Z_{k}^{T}Z_{k}=I_{r}. $$
(2.4)

Suppose that

$$ \bigl\{ \nabla h_{1}(x_{k}),\cdots ,\nabla h_{m}(x_{k}),g_{k} \bigr\} \subset S_{k}, $$
(2.5)

and \(B_{k}\in\mathbb{R}^{n\times n}\) is a symmetric matrix satisfying

$$ B_{k}u=\sigma u,\quad\forall u\in S_{k}^{\perp}, $$
(2.6)

where σ>0. Then, the subproblem (1.6)–(1.8) is equivalent to the following problem:

$$\begin{aligned} &\min_{\bar{d}\in\mathbb{R}^{r}} \bar{\phi}_{k}(\bar{d})\equiv\bar {g}_{k}^{T}\bar{d}+\frac{1}{2}\bar{d}^{T} \bar{B}_{k}\bar{d}, \end{aligned}$$
(2.7)
$$\begin{aligned} &\mathrm{s.t.}\quad \big\| c_{k}+\bar{A}_{k}^{T}\bar{d} \big\| _{2}\leqslant \xi_{k}, \end{aligned}$$
(2.8)
$$\begin{aligned} & \phantom{\mathrm{s.t.}\quad}\|\bar{d}\|_{2}\leqslant \varDelta_{k}, \end{aligned}$$
(2.9)

where \(\bar{g}_{k}=Z_{k}^{T}g_{k}\), \(\bar{B}_{k}=Z_{k}^{T}B_{k}Z_{k}\) and \(\bar{A}_{k}=Z_{k}^{T}A_{k}\). That is to say, if s k is a solution of (1.6)–(1.8), then \(s_{k}=Z_{k}\bar {s}_{k}\in S_{k}\), where \(\bar{s}_{k}\) is a solution of (2.7)–(2.9). On the other hand, if \(\bar{s}_{k}\) is a solution of (2.7)–(2.9), then \(s_{k}=Z_{k}\bar{s}_{k}\) is a solution of (1.6)–(1.8).

Proof

Let \(U_{k}\in\mathbb{R}^{n\times(n-r)}\) be a matrix such that [U k ,Z k ] is an n×n orthogonal matrix. Then, for each \(d\in\mathbb{R}^{n}\), there exists one and only one pair \(\bar {d}\in\mathbb{R}^{r}\), \(u\in\mathbb{R}^{n-r}\) such that \(d=Z_{k}\bar {d}+U_{k}u\). As B k is symmetric, it follows that

$$\begin{aligned} \phi_{k}(d) =&g_{k}^{T}d+\frac{1}{2}d^{T}B_{k}d \\ =&g_{k}^{T} [Z_{k}\bar{d}+U_{k}u ]+ \frac{1}{2} [Z_{k}\bar {d}+U_{k}u ]^{T}B_{k} [Z_{k}\bar{d}+U_{k}u ] \\ =&g_{k}^{T}Z_{k}\bar{d}+g_{k}^{T}U_{k}u+ \frac{1}{2}\bar {d}^{T}Z_{k}^{T}B_{k}Z_{k} \bar{d}+\frac{1}{2}\bar {d}^{T}Z_{k}^{T}B_{k}U_{k}u \\ &{}+\frac{1}{2}u^{T}U_{k}^{T}B_{k}Z_{k} \bar{d}+\frac {1}{2}u^{T}U_{k}^{T}B_{k}U_{k}u \\ =&g_{k}^{T}Z_{k}\bar{d}+g_{k}^{T}U_{k}u+ \frac{1}{2}\bar {d}^{T}Z_{k}^{T}B_{k}Z_{k} \bar{d}+\bar {d}^{T}Z_{k}^{T}B_{k}U_{k}u \\ &{}+\frac{1}{2}u^{T}U_{k}^{T}B_{k}U_{k}u \\ =&\bar{g}_{k}^{T}\bar{d}+g_{k}^{T}U_{k}u+ \frac{1}{2}\bar{d}^{T}\bar {B}_{k}\bar{d}+ \bar{d}^{T}Z_{k}^{T}B_{k}U_{k}u \\ &{}+\frac{1}{2}u^{T}U_{k}^{T}B_{k}U_{k}u, \end{aligned}$$
(2.10)

where \(\bar{g}_{k}=Z_{k}^{T}g_{k}\) and \(\bar {B}_{k}=Z_{k}^{T}B_{k}Z_{k}\). Since g k ∈S k and the columns of U k are vectors in \(S_{k}^{\perp}\), we obtain

$$\begin{aligned} g_{k}^{T}U_{k} =&0, \end{aligned}$$
(2.11)
$$\begin{aligned} Z_{k}^{T}B_{k}U_{k} =&\sigma Z_{k}^{T}U_{k}=0\quad\text{and}\quad U_{k}^{T}B_{k}U_{k}=\sigma I_{n-r}, \end{aligned}$$
(2.12)

where the last line is due to the assumption (2.6). Hence, (2.10)–(2.12) imply that

$$ \phi_{k}(d)= \biggl(\bar{g}_{k}^{T}\bar{d}+ \frac{1}{2}\bar{d}^{T}\bar {B}_{k}\bar{d} \biggr)+ \frac{1}{2}\sigma u^{T}u. $$
(2.13)

From the fact that the rows of \(A_{k}^{T}\) are the vectors ∇h i (x k )∈S k and the columns of U k belong to \(S_{k}^{\perp}\), it follows that \(A_{k}^{T}U_{k}=0\). Consequently,

$$ \big\| c_{k}+A_{k}^{T}d\big\| _{2}= \big\| c_{k}+A_{k}^{T}Z_{k}\bar{d} \big\| _{2}=\big\| c_{k}+\bar{A}_{k}^{T}\bar{d} \big\| _{2}, $$
(2.14)

where \(\bar{A}_{k}=Z_{k}^{T}A_{k}\). In addition, by the orthonormality of Z k and U k , we have

$$ \|d\|_{2}^{2}=\|\bar{d}\|_{2}^{2}+\|u \|_{2}^{2}. $$
(2.15)

Now, (2.13)–(2.15) imply that the subproblem (1.6)–(1.8) is equivalent to

$$\begin{aligned} &\min_{\bar{d}\in\mathbb{R}^{r},u\in\mathbb{R}^{n-r}}\, \biggl(\bar {g}_{k}^{T} \bar{d}+\frac{1}{2}\bar{d}^{T}\bar{B}_{k}\bar{d} \biggr)+\frac{1}{2}\sigma u^{T}u, \end{aligned}$$
(2.16)
$$\begin{aligned} &\text{s.t.}\quad \big\| c_{k}+\bar{A}_{k}^{T}\bar{d} \big\| _{2}\leqslant \xi_{k} , \end{aligned}$$
(2.17)
$$\begin{aligned} &\phantom{\text{s.t.}\quad} \|\bar{d}\|_{2}^{2}+\|u\|_{2}^{2}\leqslant \varDelta_{k}^{2}, \end{aligned}$$
(2.18)

with the relation \(d=Z_{k}\bar{d}+U_{k}u\).

Because of σ>0, if \(\bar{s}_{k}\) is a solution of (2.7)–(2.9) then \((\bar{s}_{k},0)\in\mathbb{R}^{r}\times \mathbb{R}^{n-r}\) is a solution of (2.16)–(2.18) and, therefore, \(s_{k}=Z_{k}\bar{s}_{k}\) is a solution of (1.6)–(1.8). To prove the reciprocal, we assume by contradiction that there exists a solution \(s_{k}=Z_{k}\bar {s}_{k}+U_{k}u_{k}\) of (1.6)–(1.8) such that u k ≠0. In this case,

$$ \phi_{k}(s_{k})\leqslant \phi_{k}(s), $$
(2.19)

for all \(s\in \mathbb{R}^{n}\) satisfying (1.7)–(1.8). In particular,

$$ \phi_{k}(s_{k})\leqslant \phi_{k} \bigl(s_{k}^{*}\bigr), $$
(2.20)

where \(s_{k}^{*}=Z_{k}\bar{s}_{k}\). However, since u k ≠0 and σ>0, from (2.13) it follows that

$$ \phi_{k}(s_{k})>\bar{g}_{k}^{T} \bar{s}_{k}+\frac{1}{2}\bar {s}_{k}^{T} \bar{B}_{k}\bar{s}_{k}=\phi_{k} \bigl(s_{k}^{*}\bigr), $$
(2.21)

which contradicts (2.20). This shows that if s k is a solution of (1.6)–(1.8) then \(s_{k}=Z_{k}\bar{s}_{k}\). The fact that \(\bar{s}_{k}\) is a solution of (2.7)–(2.9) follows from the equivalence between (1.6)–(1.8) and (2.16)–(2.18) with u=0. □

Remark 2.1

From the above lemma, if the assumptions (2.4)–(2.6) are satisfied, then we can solve the subproblem (2.7)–(2.9) in \(\mathbb{R}^{r}\) instead of solving the subproblem (1.6)–(1.8) in \(\mathbb{R}^{n}\), which can reduce the computational efforts significantly when r≪n.

Remark 2.2

For the further analysis, it is useful to see that

$$ B_{k}u=\sigma u,\quad\forall u\in G_{k}^{\perp} \quad\Longrightarrow\quad B_{k}z\in G_{k},\quad\forall z\in G_{k}. $$
(2.22)

Indeed, given z∈G k and \(u\in G_{k}^{\perp}\), as B k is a symmetric matrix, we have

$$\begin{aligned} \langle B_{k}z,u \rangle_{2} =& \bigl\langle z,B_{k}^{T}u \bigr\rangle _{2}= \langle z,B_{k}u \rangle_{2} \\ =& \langle z,\sigma u \rangle_{2} =\sigma \langle z,u \rangle_{2}=0. \end{aligned}$$

Thus, \(B_{k}z\in (G_{k}^{\perp} )^{\perp}=G_{k}\) for all z∈G k .

Lemma 2.3

Suppose that \(\xi_{1}>\min_{\|d\|_{2}\leqslant \varDelta_{1}} \| c_{1}+A_{1}^{T}d\|_{2}\), B 1=σI n (σ>0) and B k is the kth update matrix given by one formula chosen from PSB and Broyden family. Let g k =∇f(x k ), s k be a solution of (1.6)–(1.8) and

$$ G_{k}=\mathrm{span} \Biggl[\bigcup_{i=1}^{k} \bigl\{ \nabla h_{1}(x_{i}),\cdots ,\nabla h_{m}(x_{i}),g_{i} \bigr\} \Biggr]. $$
(2.23)

Then, for all k, s k ∈G k and B k u=σu for all \(u\in G_{k}^{\perp}\).

Proof

The PSB formula and Broyden family formulas (see, e.g., Sun and Yuan [13]) can be represented, respectively, as

$$\begin{aligned} B_{k+1}^{(\mathrm{PSB})} =&B_{k}^{(\mathrm{PSB})}+ \frac{\delta_{k}s_{k}^{T}+s_{k}\delta _{k}^{T}}{s_{k}^{T}s_{k}}-\frac{(\delta _{k}^{T}s_{k})s_{k}s_{k}^{T}}{(s_{k}^{T}s_{k})^{2}}, \end{aligned}$$
(2.24)
$$\begin{aligned} B_{k+1}^{(B)} =&B_{k}^{(B)}- \frac {B_{k}^{(B)}s_{k}s_{k}^{T}B_{k}^{(B)}}{s_{k}^{T}B_{k}s_{k}}+\frac {y_{k}y_{k}^{T}}{s_{k}^{T}y_{k}}+\theta _{k}\bigl(s_{k}^{T}B_{k}^{(B)}s_{k} \bigr)w_{k}w_{k}^{T}, \end{aligned}$$
(2.25)

where s k =x k+1−x k , y k =(g k+1−g k )−(A k+1 λ k+1−A k λ k ) or y k =(g k+1−g k )−(A k+1−A k )λ k , \(\delta _{k}=y_{k}-B_{k}^{(\mathrm{PSB})}s_{k}\) and

$$ w_{k}=\frac{y_{k}}{s_{k}^{T}y_{k}}-\frac {B_{k}^{(B)}s_{k}}{s_{k}^{T}B_{k}^{(B)}s_{k}}. $$
(2.26)

We prove the result by induction over k. By Lemma 2.1 and σ>0,

$$\begin{aligned} & \bigl(B_{1}+\alpha_{1}I_{n}+ \beta_{1}A_{1}A_{1}^{T} \bigr)s_{1}=- (g_{1}+\beta_{1}A_{1}c_{1} ) \\ &\quad\Longrightarrow\quad \bigl(\sigma I_{n}+\alpha_{1}I_{n}+ \beta _{1}A_{1}A_{1}^{T} \bigr)s_{1}=- (g_{1}+\beta_{1}A_{1}c_{1} ) \\ &\quad\Longrightarrow\quad (\sigma+\alpha_{1} )s_{1}=- \bigl(g_{1}+\beta _{1}A_{1}c_{1}+ \beta_{1}A_{1}A_{1}^{T}s_{1} \bigr) \\ &\quad\Longrightarrow\quad s_{1}=- (\sigma+\alpha_{1} )^{-1} \bigl(g_{1}+\beta_{1}A_{1}c_{1}+ \beta_{1}A_{1}A_{1}^{T}s_{1} \bigr) \\ &\quad\Longrightarrow\quad s_{1}\in G_{1}, \end{aligned}$$

where the last line is true because g 1, A 1 c 1 and \(A_{1}A_{1}^{T}s_{1}\in G_{1}\). Moreover,

$$ B_{1}^{(\mathrm{PSB})}u=B_{1}^{(B)}u=(\sigma I_{n})u=\sigma u,\quad\forall u\in G_{1}^{\perp}. $$
(2.27)

Hence, the lemma is true for k=1. Assume that the lemma is true for k=i, that is,

$$ s_{i}\in G_{i}, $$
(2.28)

and

$$ B_{i}^{(\mathrm{PSB})}u=B_{i}^{(B)}u=\sigma u,\quad \forall u\in G_{i}^{\perp}. $$
(2.29)

Consider \(\tilde{u}\in G_{i+1}^{\perp}\). In particular, we have \(\tilde {u}\in G_{i}^{\perp}\) (since \(G_{i}\subset G_{i+1}\Longrightarrow G_{i+1}^{\perp}\subset G_{i}^{\perp}\)). Then, as y i ∈G i+1 and \(B_{i}^{(\mathrm{PSB})}\) and \(B_{i}^{(B)}\) are symmetric matrices, it follows from (2.28) and (2.29) that

$$\begin{aligned} B_{i+1}^{(\mathrm{PSB})}\tilde{u} =&B_{i}^{(\mathrm{PSB})} \tilde{u}+\frac{ (\delta _{i}s_{i}^{T}+s_{i}\delta_{i}^{T} )\tilde {u}}{s_{i}^{T}s_{i}}-\frac{(\delta_{i}^{T}s_{i})s_{i}s_{i}^{T}\tilde {u}}{ (s_{i}^{T}s_{i} )^{2}} \\ =&\sigma\tilde{u}+\frac{\delta_{i}s_{i}^{T}\tilde{u}+s_{i} (y_{i}^{T}\tilde{u}-s_{i}^{T}B_{i}^{(\mathrm{PSB})}\tilde{u} )}{s_{i}^{T}s_{i}} \\ =&\sigma\tilde{u}-\sigma\frac{s_{i}s_{i}^{T}\tilde {u}}{s_{i}^{T}s_{i}} \\ =&\sigma\tilde{u}, \end{aligned}$$

and

$$\begin{aligned} B_{i+1}^{(B)}\tilde{u} =&B_{i}^{(B)} \tilde{u}-\frac {B_{i}^{(B)}s_{i}s_{i}^{T}B_{i}^{(B)}\tilde {u}}{s_{i}^{T}B_{i}s_{i}}+\frac{y_{i}y_{i}^{T}\tilde {u}}{s_{i}^{T}y_{i}}+\theta _{i} \bigl(s_{i}^{T}B_{i}^{(B)}s_{i} \bigr)w_{i}w_{i}^{T}\tilde{u} \\ =&\sigma\tilde{u}-\frac{\sigma B_{i}^{(B)}s_{i}s_{i}^{T}\tilde {u}}{s_{i}^{T}B_{i}^{(B)}s_{i}}+\theta _{i}\bigl(s_{i}^{T}B_{i}^{(B)}s_{i} \bigr)w_{i} \biggl(\frac {y_{i}^{T}}{s_{i}^{T}y_{i}}-\frac {s_{i}^{T}B_{i}^{(B)}}{s_{i}^{T}B_{i}^{(B)}s_{i}} \biggr) \tilde{u} \\ =&\sigma\tilde{u} +\theta_{i}\bigl(s_{i}^{T}B_{i}^{(B)}s_{i} \bigr)w_{i} \biggl(\frac{y_{i}^{T}\tilde{u}}{s_{i}^{T}y_{i}}-\frac {s_{i}^{T}B_{i}^{(B)}\tilde{u}}{s_{i}^{T}B_{i}^{(B)}s_{i}} \biggr) \\ =&\sigma\tilde{u}-\sigma\theta _{i}\bigl(s_{i}^{T}B_{i}^{(B)}s_{i} \bigr)w_{i}\frac{s_{i}^{T}\tilde {u}}{s_{i}^{T}B_{i}^{(B)}s_{i}} \\ =&\sigma\tilde{u}. \end{aligned}$$

Since \(\tilde{u}\in G_{i+1}^{\perp}\) is arbitrary, this proves that

$$ B_{i+1}^{(\mathrm{PSB})}u=B_{i+1}^{(B)}u=\sigma u,\quad \forall u\in G_{i+1}^{\perp}. $$
(2.30)

Now, let s i+1 be a solution of the subproblem (1.6)–(1.8) for k=i+1. Then, by

$$ \bigl\{ \nabla h_{1}(x_{i+1}),\cdots ,\nabla h_{m}(x_{i+1}),g_{i+1} \bigr\} \subset G_{i+1}, $$

equation (2.30) and Lemma 2.2 (where k=i+1), we conclude that \(s_{i+1}=Z_{i+1}\bar{s}_{i+1}\in G_{i+1}\) (where \(\bar{s}_{i+1}\) is a solution of the subproblem (2.7)–(2.9) for k=i+1, and Z i+1 is an orthonormal basis matrix of G i+1). The proof is complete. □

Remark 2.3

The result of Lemma 2.3 also is true if the matrices B k are updated by the family of formulas

$$ B_{k+1}=B_{k}-\frac {B_{k}s_{k}s_{k}^{T}B_{k}}{s_{k}^{T}B_{k}s_{k}}+\frac{\eta_{k}\eta _{k}^{T}}{s_{k}^{T}\eta_{k}}, $$
(2.31)

where η k =θ k y k +(1−θ k )B k s k with θ k ∈[0,1], which includes the damped BFGS formula of Powell [10]. Indeed, if B 1=σI n (σ>0) and \(\xi_{1}>\min_{\|d\|_{2}\leqslant \varDelta_{1}} \|c_{1}+A_{1}^{T}d\|_{2}\), then by the same argument used in the proof of Lemma 2.3 we conclude that s 1∈G 1 and B 1 u=σu for all \(u\in G_{1}^{\perp}\). Thus, the result is true for k=1. Assume that it is true for k=i, that is,

$$ s_{i}\in G_{i}, $$
(2.32)

and

$$ B_{i}u=\sigma u,\quad\forall u\in G_{i}^{\perp}. $$
(2.33)

Then, from Remark 2.2 it follows that B i s i ∈G i ⊂G i+1. As y i ∈G i+1, we also have η i =θ i y i +(1−θ i )B i s i ∈G i+1. Now, given \(\tilde {u}\in G_{i+1}^{\perp}\subset G_{i}^{\perp}\), it follows from (2.32) and (2.33) that

$$\begin{aligned} B_{i+1}\tilde{u} =&B_{i}\tilde{u}-\frac{B_{i}s_{i}s_{i}^{T}B_{i}\tilde {u}}{s_{i}^{T}B_{i}s_{i}}+ \frac{\eta_{i}\eta_{i}^{T}\tilde {u}}{s_{i}^{T}\eta_{i}} \\ =&\sigma\tilde{u}-\frac{\sigma B_{i}s_{i}s_{i}^{T}\tilde {u}}{s_{i}^{T}B_{i}s_{i}} \\ =&\sigma\tilde{u}. \end{aligned}$$

Since \(\tilde{u}\in G_{i+1}^{\perp}\) is arbitrary, this proves that

$$ B_{i+1}u=\sigma u,\quad\forall u\in G_{i+1}^{\perp}. $$
(2.34)

Therefore, the conclusion follows by induction in the same way as in the proof of Lemma 2.3.

By Lemmas 2.2, 2.3 and Remark 2.3, we obtain the following theorem.

Theorem 2.1

Let Z k be an orthonormal basis matrix of the subspace

$$ G_{k}=\mathrm{span} \Biggl[\bigcup_{i=1}^{k} \bigl\{ \nabla h_{1}(x_{i}),\cdots ,\nabla h_{m}(x_{i}),g_{i} \bigr\} \Biggr]. $$
(2.35)

Suppose that \(\xi_{1}>\min_{\|d\|_{2}\leqslant \varDelta_{1}} \| c_{1}+A_{1}^{T}d\|_{2}\), B 1=σI n (σ>0) and B k is the kth update matrix given by one formula chosen from damped BFGS, PSB and Broyden family. Let s k be a solution of the subproblem (1.6)–(1.8). Then, there exists a solution \(\bar{s}_{k}\) of (2.7)–(2.9) such that \(s_{k}=Z_{k}\bar {s}_{k}\), which implies s k ∈G k . Reciprocally, if \(\bar {s}_{k}\) is a solution of (2.7)–(2.9), then \(s_{k}=Z_{k}\bar{s}_{k}\) is a solution of (1.6)–(1.8).

From the above theorem, the trial step s k is in the subspace G k . Hence, we can update the approximate Hessian matrix B k in the subspace G k by the damped BFGS formula, the PSB formula or any one from the Broyden family. The following result has been given by Siegel [12] and Gill and Leonard [5] for Broyden family, and by Wang and Yuan [14] including the PSB formula. We give it here for completeness.

Lemma 2.4

Let \(Z\in\mathbb{R}^{n\times r}\) be a column orthogonal matrix. Suppose that s k ∈span{Z}, and the matrix B k+1=Update(B k ,s k ,y k ) is obtained by the damped BFGS formula, the PSB formula or any one from the Broyden family. Then, denoting \(\bar{B}_{k+1}=Z^{T}B_{k+1}Z\), \(\tilde {B}_{k}=Z^{T}B_{k}Z\), \(\tilde{s}_{k}=Z^{T}s_{k}\) and \(\tilde {y}_{k}=Z^{T}y_{k}\), we have \(\bar{B}_{k+1}=\mathit{Update} (\tilde {B}_{k},\tilde{s}_{k},\tilde{y}_{k} )\).

Proof

First, note that

$$ s_{k}\in\mathrm{span} \{Z \}\quad\Longrightarrow\quad s_{k}=ZZ^{T}s_{k}. $$
(2.36)

Then,

$$\begin{aligned} s_{k}^{T}y_{k} =&\bigl(ZZ^{T}s_{k} \bigr)^{T}y_{k}= \bigl(Z^{T}s_{k} \bigr)^{T}Z^{T}y_{k}=\tilde{s}_{k}^{T} \tilde{y}_{k}, \\ s_{k}^{T}B_{k}s_{k} =& \bigl(ZZ^{T}s_{k}\bigr)^{T}B_{k} \bigl(ZZ^{T}s_{k}\bigr)= \bigl(Z^{T}s_{k} \bigr)^{T}Z^{T}B_{k}Z \bigl(Z^{T}s_{k} \bigr)=\tilde {s}_{k}^{T}\tilde{B}_{k} \tilde{s}_{k}, \\ Z^{T}B_{k}s_{k} =&Z^{T}B_{k}Z \bigl(Z^{T}s_{k} \bigr)=\tilde {B}_{k} \tilde{s}_{k}. \end{aligned}$$

Therefore, multiplying (2.24), (2.25), and (2.31) by Z T from the left and Z from the right, we can obtain the result of the lemma. □

Remark 2.4

By Theorem 2.1, we can solve the CDT subproblem (1.6)–(1.8) by solving (2.7)–(2.9) in the subspace G k , provided that ξ 1 and B 1 are appropriately chosen and a suitable quasi-Newton formula is used to update B k . Further, it follows from Lemma 2.4 that the reduced matrix \(\bar {B}_{k}=Z_{k}^{T}B_{k}Z_{k}\) of B k in the subspace G k can be obtained by updating the reduced matrix \(\tilde {B}_{k-1}=Z_{k}^{T}B_{k-1}Z_{k}\), where Z k is the orthonormal basis matrix of the subspace G k . These subspace properties can be explored to reduce the amount of computation required to compute the trial step s k when n≫m and the dimension of the subspace G k remains far smaller than n.

3 The Algorithm

Using the subspace properties of the CDT subproblem studied in the previous section, we shall construct a subspace version of Algorithm 1.1. Suppose at the kth iteration, \(Z_{k}\in\mathbb{R}^{n\times r_{k}}\) has been obtained, which is an orthonormal basis matrix of G k . Further, suppose that \(\bar{s}_{k}\) is obtained by solving (2.7)–(2.9) and \(s_{k}=Z_{k}\bar{s}_{k}\), x k+1=x k +s k and g k+1=∇f(x k+1). Then, we have to compute Z k+1, \(\bar{g}_{k+1}=Z_{k+1}^{T}g_{k+1}\), \(\bar {A}_{k+1}=Z_{k+1}^{T}A_{k+1}\) and \(\bar {B}_{k+1}=Z_{k+1}^{T}B_{k+1}Z_{k+1}\) for the next iteration.

Thinking about numerical stability, as in Wang and Yuan [14], we could use the procedure of Gram–Schmidt with reorthogonalization (see Sect. 2 in Daniel et al. [3]) to obtain Z k+1. For this purpose, consider the notation:

$$ p_{j}^{(k+1)}=\left \{ \begin{array}{l@{\quad}l} \nabla h_{j}(x_{k+1}),& j=1,\cdots ,m,\\ g_{k+1}, & j=m+1. \end{array} \right . $$
(3.1)

Let W 1=Z k and q 1=r k , where r k denotes the number of columns of Z k . For j=1,⋯,m+1, by the reorthogonalization procedure, compute the decomposition

$$ p_{j}^{(k+1)}=W_{j}u_{j}^{(k)}+ \tau_{j}^{(k+1)}z_{j}^{(k+1)}, $$
(3.2)

where

$$ u_{j}^{(k)}=W_{j}^{T}p_{j}^{(k+1)}, \qquad z_{j}^{(k+1)}\perp\text {span} \{W_{j} \},\qquad \big\| z_{j}^{(k+1)}\big\| _{2}=1, $$
(3.3)

and

$$ \tau_{j}^{(k+1)}=\big\| \bigl(I-W_{j}W_{j}^{T} \bigr)p_{j}^{(k+1)}\big\| _{2}\geqslant 0. $$
(3.4)

If \(\tau_{j}^{(k+1)}>0\), it follows that \(p_{j}^{(k+1)}\notin\text {span} \{W_{j} \}\), and we set

$$ W_{j+1}= \bigl[W_{j}\quad z_{j}^{(k+1)} \bigr]\quad\text{and}\quad q_{j+1}=q_{j}+1. $$
(3.5)

Otherwise, it follows that \(p_{j}^{(k+1)}\in\mathrm{span} \{ W_{j} \}\), and we set

$$ W_{j+1}=W_{j}\quad\text{and}\quad q_{j+1}=q_{j}. $$
(3.6)

At the end of the loop, we obtain Z k+1=W m+2 and r k+1=q m+2.

Now, using the data obtained in the calculation of Z k+1, we can compute \(\bar{g}_{k+1}\), \(\bar{A}_{k+1}\) and \(\bar{B}_{k+1}\) in a cheaper way. Indeed, from (3.2), (3.3), and the fact that s k , g k ∈span{W j }, it follows that

$$ \bigl(z_{j}^{(k+1)} \bigr)^{T}p_{j}^{(k+1)}= \tau_{j}^{(k+1)},\qquad \bigl(z_{j}^{(k+1)} \bigr)^{T}s_{k}=0,\qquad \bigl(z_{j}^{(k+1)} \bigr)^{T}g_{k}=0. $$
(3.7)

If Z k+1≠Z k , that is, \(Z_{k+1}= [Z_{k}\ \bar{Z}_{k+1} ]\), then Lemma 2.3 and Remark 2.2 imply that \(B_{k}\bar {Z}_{k+1}=\sigma\bar{Z}_{k+1}\) and the columns of B k Z k belong to G k . Thus, denoting q=r k+1−r k , we get

$$\begin{aligned} \tilde{s}_{k} =&Z_{k+1}^{T}s_{k}= \left [ \begin{array}{c} Z_{k}^{T}s_{k}\\ \bar{Z}_{k+1}^{T}s_{k} \end{array} \right ] =\left [ \begin{array}{c} \bar{s}_{k}\\ 0 \end{array} \right ], \end{aligned}$$
(3.8)
$$\begin{aligned} \tilde{B}_{k} =&Z_{k+1}^{T}B_{k}Z_{k+1}= \left [ \begin{array}{c}Z_{k}^{T}\\ \bar{Z}_{k+1}^{T} \end{array} \right ]B_{k} [Z_{k}\quad\bar{Z}_{k+1} ] \\ =&\left [ \begin{array}{c}Z_{k}^{T}\\ \bar{Z}^T_{k+1} \end{array} \right ] [B_{k}Z_{k} \quad B_{k}\bar{Z}_{k+1} ]=\left [ \begin{array}{c} Z_{k}^{T}\\ \bar{Z}_{k+1}^{T} \end{array} \right ] [B_{k}Z_{k}\quad\sigma \bar{Z}_{k+1} ] \\ =&\left [ \begin{array}{c@{\quad}c} Z_{k}^{T}B_{k}Z_{k} &\sigma Z_{k}^{T}\bar{Z}_{k+1}\\ \bar{Z}_{k+1}^TB_{k}Z_{k}&\sigma\bar{Z}_{k+1}^{T}\bar{Z}_{k+1} \end{array} \right ]=\left [ \begin{array}{c@{\quad}c}\bar{B}_{k}&0\\ 0&\sigma I_{q} \end{array} \right ]. \end{aligned}$$
(3.9)

To compute \(\bar{g}_{k+1}\), from (3.3) and (3.1), note that

$$\begin{aligned} W_{m+1}^{T}p_{m+1}^{(k+1)}=u_{m+1}^{(k)} \quad \Longrightarrow&\quad W_{m+1}^{T}g_{k+1}=u_{m+1}^{(k)} \\ \Longrightarrow&\quad [Z_{k}\quad\tilde{Z}_{k+1} ]^{T}g_{k+1}=u_{m+1}^{(k)} \\ \Longrightarrow&\quad Z_{k}^{T}g_{k+1}= \bigl[ \bigl(u_{m+1}^{(k)} \bigr)_{1}\quad \cdots \quad \bigl(u_{m+1}^{(k)} \bigr)_{r_{k}} \bigr]^{T}, \end{aligned}$$
(3.10)

where the columns of \(\tilde{Z}_{k+1}\) are distinct vectors of the set \(\{z_{1}^{(k+1)},\cdots ,z_{m+1}^{(k+1)} \}\). Further,

$$\begin{aligned} \bar{Z}_{k+1}^{T}W_{m+1} =&\bar{Z}_{k+1}^{T} [Z_{k}\quad\tilde {Z}_{k+1} ] \\ =& \bigl[0 \quad\bar {Z}_{k+1}^{T}\tilde{Z}_{k+1} \bigr] \\ =&\left \{ \begin{array}{l@{\quad}l} \left [ \begin{array}{c|c} 0&I_{q-1}\\ \hline 0\cdots 0 & 0 \cdots 0 \end{array} \right ],& \text{if}\ \tau_{m+1}^{(k+1)}>0, \\ \left [ \begin{array}{c@{\quad}c} 0&I_{q} \end{array} \right ],& \text{otherwise}. \end{array} \right . \end{aligned}$$
(3.11)

Then, multiplying (3.2) from the left by \(\bar {Z}_{k+1}\) (with j=m+1), we obtain

$$\begin{aligned} \bar{Z}_{k+1}^{T}g_{k+1} =&\bar{Z}_{k+1}^{T}W_{m+1}u_{m+1}^{(k)}+ \tau _{m+1}^{(k+1)}\bar{Z}_{k+1}^{T}z_{m+1}^{(k+1)} \\ =&\left\{ \begin{array}{l@{\quad}l} [ (u_{m+1}^{(k)} )_{r_{k}+1}\cdots (u_{m+1}^{(k)} )_{r_{k+1}-1}\,\tau_{m+1}^{(k+1)} ]^{T},&\text {if}\ \tau_{m+1}^{(k+1)}>0,\\ {}[ (u_{m+1}^{(k)} )_{r_{k}+1}\cdots (u_{m+1}^{(k)} )_{r_{k+1}} ]^{T},& \text{otherwise}. \end{array} \right. \end{aligned}$$
(3.12)

Hence, combining (3.10) and (3.12), we have

$$\begin{aligned} \bar{g}_{k+1} =&Z_{k+1}^{T}g_{k+1}=\left [ \begin{array}{c}Z_{k}^{T}g_{k+1}\\ \bar{Z}^{T}_{k+1}g_{k+1} \end{array} \right ] \\ =&\left \{ \begin{array}{l@{\quad}l} [ (u_{m+1}^{(k)} )_{1}\cdots (u_{m+1}^{(k)} )_{r_{k+1}-1}\,\tau_{m+1}^{(k+1)} ]^{T},&\text{if}\ \tau _{m+1}^{(k+1)}>0,\\ {}[ (u_{m+1}^{(k)} )_{1}\cdots (u_{m+1}^{(k)} )_{r_{k+1}} ]^{T},& \text{otherwise}. \end{array} \right . \end{aligned}$$
(3.13)

By (3.1),

$$\begin{aligned} \bar{A}_{k+1} =&Z_{k+1}^{T}A_{k+1}=\left [ \begin{array}{c}Z_{k}^{T}A_{k+1}\\ \bar{Z}_{k+1}^{T}A_{k+1} \end{array} \right ] \\ =&\left [ \begin{array}{c} [Z_{k}^{T}p_{1}^{(k+1)}\quad \cdots \quad Z_{k}^{T}p_{m}^{(k+1)} ]\\ {}[\bar{Z}_{k+1}^{T}p_{1}^{(k+1)}\quad \cdots \quad \bar {Z}_{k+1}^{T}p_{m}^{(k+1)} ] \end{array} \right ]. \end{aligned}$$
(3.14)

Thus, denoting

$$ \bar{U}_{k+1}= \bigl[Z_{k}^{T}p_{1}^{(k+1)} \quad \cdots \quad Z_{k}^{T}p_{m}^{(k+1)} \bigr] $$
(3.15)

and

$$ \tilde{U}_{k+1}= \bigl[\bar{Z}_{k+1}^{T}p_{1}^{(k+1)} \quad \cdots \quad \bar {Z}_{k+1}^{T}p_{m}^{(k+1)} \bigr], $$
(3.16)

it follows that

$$ \bar{A}_{k+1}=\left [ \begin{array}{c}\bar{U}_{k+1}\\ \tilde{U}_{k+1} \end{array} \right ]. $$
(3.17)

Again, by (3.3), for each j=1,⋯,m,

$$\begin{aligned} W_{j}^{T}p_{j}^{(k+1)}=u_{j}^{(k)}\quad \Longrightarrow&\quad \bigl[Z_{k}\quad \tilde{Z}_{k+1}^{j} \bigr]^{T}p_{j}^{(k+1)}=u_{j}^{(k)} \\ \Longrightarrow&\quad Z_{k}^{T}p_{j}^{(k+1)}= \bigl[ \bigl(u_{j}^{(k)} \bigr)_{1}\quad \cdots \quad\bigl(u_{j}^{(k)} \bigr)_{r_{k}} \bigr]^{T}, \end{aligned}$$
(3.18)

where the columns of \(\tilde{Z}_{k+1}^{j}\) are distinct vectors of the set \(\{z_{1}^{(k+1)},\cdots ,z_{j}^{(k+1)} \}\). Further, multiplying (3.2) from the left by \(\bar{Z}_{k+1}\), we obtain

$$ \bar{Z}_{k+1}^{T}p_{j}^{(k+1)}=\left \{ \begin{array}{l@{\quad}l} [ (u_{j}^{(k)} )_{r_{k}+1}\cdots (u_{j}^{(k)} )_{q_{j}}\tau_{j}^{(k+1)}0\cdots 0 ]^{T},&\text{if}\ \tau_{j}^{(k+1)}>0,\\ {}[ (u_{j}^{(k)} )_{r_{k}+1}\cdots (u_{j}^{(k)} )_{q_{j}}0\cdots 0 ]^{T},& \text{otherwise}, \\ \end{array} \right . $$
(3.19)

for each j=1,⋯,m, which completes the computation of \(\bar{A}_{k+1}\).

Finally, if y k =(g k+1−g k )−(A k+1 λ k+1−A k λ k ) thenFootnote 1

$$\begin{aligned} \tilde{y}_{k} =&Z_{k+1}^{T}y_{k}= \left [ \begin{array}{c} Z_{k}^{T}y_{k}\\ \bar{Z}_{k+1}^{T}y_{k} \end{array} \right ] \\ =&\left [ \begin{array}{c} Z_{k}^{T} [g_{k+1}-g_{k}-A_{k+1}\lambda _{k+1}+A_{k}\lambda_{k} ]\\ \bar{Z}_{k+1}^{T} [g_{k+1}-g_{k}-A_{k+1}\lambda_{k+1}+A_{k}\lambda _{k} ] \end{array} \right ] \\ =&\left [ \begin{array}{c} Z_{k}^{T}g_{k+1}-\bar{g}_{k}-\bar{U}_{k+1}\lambda _{k+1}+\bar{A}_{k}\lambda_{k}\\ \bar{Z}_{k+1}^{T}g_{k+1}-\tilde{U}_{k+1}\lambda_{k+1} \end{array} \right ]. \end{aligned}$$
(3.20)

For the case in which Z k+1=Z k , it follows that

$$\begin{aligned} \tilde{s}_{k} =&Z_{k}^{T}s_{k}= \bar{s}_{k}, \end{aligned}$$
(3.21)
$$\begin{aligned} \tilde{B}_{k} =&Z_{k}^{T}B_{k}Z_{k}= \bar{B}_{k}, \end{aligned}$$
(3.22)
$$\begin{aligned} \bar{g}_{k+1} =&Z_{k}^{T}g_{k+1}= \bigl[ \bigl(u_{m+1}^{(k)} \bigr)_{1}\quad \cdots \quad \bigl(u_{m+1}^{(k)} \bigr)_{r_{k}} \bigr]^{T}, \end{aligned}$$
(3.23)
$$\begin{aligned} \bar{A}_{k+1} =&Z_{k}^{T}A_{k+1}= \bar{U}_{k+1}, \end{aligned}$$
(3.24)
$$\begin{aligned} \tilde{y}_{k} =&Z_{k}^{T}y_{k}= \bar{g}_{k+1}-\bar{g}_{k}-\bar {U}_{k+1} \lambda_{k+1}+\bar{A}_{k}\lambda_{k}. \end{aligned}$$
(3.25)

According to Lemma 2.4, the reduced matrix

$$\bar{B}_{k+1}=Z_{k+1}^{T}B_{k+1}Z_{k+1} $$

in the subspace span{Z k+1} can be obtained by any formula among the damped BFGS, PSB and Broyden family, by use of \(\tilde{s}_{k}\), \(\tilde{B}_{k}\) and \(\tilde{y}_{k}\) computed by (3.8), (3.9), and (3.20), or by (3.21), (3.22), and (3.25). Then, by Theorem 2.1 we can solve the subproblem (2.7)–(2.9) with the reduced matrix \(\bar {B}_{k+1}\), the reduced matrix \(\bar{A}_{k+1}\) and the reduced gradient \(\bar{g}_{k+1}\) to obtain \(\bar{s}_{k+1}\) and the trial step \(s_{k+1}=Z_{k+1}\bar{s}_{k+1}\).

We summarize the above observations in the following algorithm.

Algorithm 3.1

(Subspace Version of the Powell–Yuan Algorithm)

  1. Step 0

    Given \(x_{1}\in\mathbb{R}^{n}\), Δ 1>0, ε s >0, γ∈[0,1), μ 1>0, and 0<b 2⩽b 1<1, choose one matrix updating formula among the damped BFGS, PSB and Broyden family, and compute ∇h 1(x 1),⋯,∇h m (x 1) and g 1=∇f(x 1). Apply the procedure of Gram–Schmidt with reorthogonalization to

    $$\bigl\{ \nabla h_{1}(x_{1}),\cdots ,\nabla h_{m}(x_{1}),g_{1} \bigr\} $$

    in order to obtain a column orthogonal matrix \(Z_{1}\in\mathbb {R}^{n\times r_{1}}\) such that

    $$ \mathrm{span} \{Z_{1} \}=\mathrm{span} \bigl\{ \nabla h_{1}(x_{1}), \cdots ,\nabla h_{m}(x_{1}),g_{1} \bigr\} . $$
    (3.26)

    Set \(\bar{B}_{1}=\sigma I_{r_{1}}\), \(\bar{g}_{1}=Z_{1}^{T}g_{1}\), \(\bar {A}_{1}=Z_{1}^{T}A_{1}\) and k:=1.

  2. Step 1

    If \(\|c_{k}\|_{2}+\|\bar{g}_{k}-\bar{A}_{k}\bar{\lambda}_{k}\| _{2}\leqslant \varepsilon_{s}\) (where \(\bar{\lambda}_{k}=\bar{A}_{k}^{+}\bar{g}_{k}\)), then stop. Otherwise, compute ξ k satisfying (1.9), with \(\bar{A}_{k}\) in place of A k , and solve the CDT subproblem (2.7)–(2.9) to obtain \(\bar{s}_{k}\).

  3. Step 2

    Compute \(s_{k}=Z_{k}\bar{s}_{k}\) and D k by (1.12). If the inequality

    $$ D_{k}\leqslant \frac{1}{2}\mu_{k} \bigl( \big\| c_{k}+A_{k}^{T}s_{k} \big\| _{2}^{2}-\| c_{k}\|_{2}^{2} \bigr) $$
    (3.27)

    fails, then increase μ k to the value

    $$ \mu_{k}^{\mathrm{new}}=2\mu_{k}^{\mathrm{old}}+\max \biggl\{ 0,\frac{2D_{k}^{\mathrm{old}}}{\| c_{k}\|_{2}^{2}-\|c_{k}+A_{k}^{T}s_{k}\|_{2}^{2}} \biggr\} $$
    (3.28)

    which ensures that the new value of expression (1.12) satisfies condition (3.27).

  4. Step 3

    Compute ρ k by (1.14);

    Set x k+1 by (1.15);

    Set Δ k+1 by (1.16).

  5. Step 4

    If r k =n, set \(\bar{A}_{k+1}=A_{k+1}\), \(\bar {g}_{k+1}=g_{k+1}\), \(\tilde{s}_{k}=s_{k}\), \(\tilde{B}_{k}=\bar{B}_{k}\), \(\tilde{y}_{k}= (g_{k+1}-g_{k} )- (A_{k+1}\lambda _{k+1}-A_{k}\lambda_{k} )\), Z k+1=I n , r k+1=n and go to Step 6.

  6. Step 5

    Set W 1=Z k , q 1=r k , and consider the notation (3.1);

    For j=1:m+1

    1. (a)

      Obtain (3.2) by the reorthogonalization procedure;

    2. (b)

      If \(\tau_{j}^{(k+1)}>\gamma\|p_{j}^{(k+1)}\|_{2}\), set \(W_{j+1}= [W_{j}\quad z_{j}^{(k+1)} ]\) and q j+1=q j +1. Otherwise, set W j+1=W j and q j+1=q j .

    End(For).

    Set Z k+1=W m+2 and r k+1=q m+2;

    If Z k+1≠Z k compute \(\tilde{s}_{k}\), \(\tilde{B}_{k}\), \(\bar {g}_{k+1}\), \(\bar{A}_{k+1}\), \(\tilde{y}_{k}\) according to (3.8), (3.9), (3.13), (3.17) and (3.20), respectively. Otherwise, compute \(\tilde{s}_{k}\), \(\tilde {B}_{k}\), \(\bar{g}_{k+1}\), \(\bar{A}_{k+1}\), \(\tilde{y}_{k}\) by (3.21)–(3.25), respectively.

  7. Step 6

    Obtain \(\bar{B}_{k+1}=\mathit{Update} (\tilde {B}_{k},\tilde{s}_{k},\tilde{y}_{k} )\) by the chosen matrix updating formula. Set μ k+1:=μ k , k:=k+1 and go to Step 1.

Remark 3.1

By Step 4, when the dimension r k of the subspace span{Z k } reaches n, Algorithm 3.1 reduces to Algorithm 1.1. The reason for this step is to avoid the computational effort required by Step 5, when it is not necessary anymore.

Remark 3.2

The subspace properties of the CDT subproblem described in Sect. 2 can be used in the same way to construct a subspace version of the CDT trust-region algorithm for equality constrained optimization proposed by Celis, Dennis and Tapia [2], as well of any algorithm based on the CDT subproblem.

In order to compare Algorithms 1.1 and 3.1 with respect to the number of floating point operations per iteration, recall that n denotes the number of variables, m denotes the number of constraints and r k denotes the number of columns of the matrix Z k . First, let us consider Algorithm 3.1. The computation of \(\bar{\lambda}_{k}\) in Step 1 by Algorithm 5.3.2 in Golub and Van Loan [6] requires O(m 2 r k ) flops. As will be described in Sect. 5, the number ξ k can be obtained as a solution of an LSQI problem. In this case, the computation of ξ k in Step 1 by Algorithm 12.1.1 in Golub and Van Loan [6] requires approximately \(O(mr_{k}^{2})+O(r_{k})\) flops (see p. 208 in Bjorck [1]). Still in the Step 1, the computation of a solution of the CDT subproblem (2.7)–(2.9) by the dual algorithm of Yuan [16] requires about \(O(r_{k}^{3})+O(r_{k}^{2})+O(r_{k})\) flops.Footnote 2 The computation of \(s_{k}=Z_{k}\bar{s}_{k}\) in Step 2 requires O(nr k ) flops. The reorthogonalization procedure in Step 5 requires about O((m+1)nr k )+O(mn)+O(n) flops. Finally, the update \(\bar{B}_{k+1}\) of \(\bar{B}_{k}\) in Step 6 requires about \(O(r_{k}^{2})+O(r_{k})\) flops. Therefore, Algorithm 3.1 requires approximately

$$\begin{aligned} &O\bigl(r_{k}^{3}\bigr)+O\bigl(mr_{k}^{2} \bigr)+O\bigl(r_{k}^{2}\bigr)+O\bigl(m^{2}r_{k} \bigr)+O(r_{k})+O(nr_{k})+O\bigl((m+1)nr_{k} \bigr)\\ &\quad{}+O(mn)+O(n) \end{aligned}$$

flops for each iteration (after the first one). The Algorithm 1.1, by its turn, requires approximately

$$O\bigl(n^{3}\bigr)+O\bigl(mn^{2}\bigr)+O \bigl(n^{2}\bigr)+O\bigl(m^{2}n\bigr)+O(n) $$

flops for each iteration, with the same update formula for B k . Thus, when n is large, m is small and r k ≪n, the Algorithm 3.1 can reduce the amount of computation in comparison with the Algorithm 1.1.

4 Global Convergence

If we suppose that G k =span{Z k } and \(\xi _{1}>\min_{\|d\|_{2}\leqslant \varDelta_{1}} \|c_{1}+A_{1}^{T}d\|_{2}\) then, by Theorem 2.1 and Lemma 2.4, Algorithm 3.1 is equivalent to Algorithm 1.1. As pointed in Remark 3.1, the same is true from the moment in which r k reaches n. In both cases the global convergence of the Algorithm 3.1 follows from the fact that the Algorithm 1.1 is globally convergent (see Theorem 3.9 in Powell and Yuan [11]). In this section, we shall study the convergence of Algorithm 3.1 in a more general setting, allowing more freedom for the choice of the matrix Z k in Step 5. Specifically, we consider the assumptions:

  1. A1

    The functions \(f:\mathbb{R}^{n}\to\mathbb{R}\) and \(h_{i}:\mathbb{R}^{n}\to\mathbb{R}\) (i=1,⋯,m) are continuously differentiable;

  2. A2

    There exists a compact and convex set \(\varOmega\in \mathbb{R}^{n}\) such that x k and x k +s k are in Ω for all k;

  3. A3

    A(x) has full column rank for all x∈Ω;

  4. A4

    For each k, \(Z_{k}^{T}Z_{k}=I_{r_{k}}\), {∇h 1(x k ),⋯,∇h m (x k ),g k }⊂span{Z k } and B k z∈span{Z k } for all z∈span{Z k }.

  5. A5

    The sequence \((\|\bar{B}_{k}\|_{2} )_{k\in \mathbb{N}}\) is bounded.

We also consider the following remark, which will be extensively called in the proofs.

Remark 4.1

From \(Z_{k}^{T}Z_{k}=I_{r_{k}}\), it follows that

$$ v\in\mathrm{span} \{Z_{k} \}\quad\Longrightarrow\quad v=Z_{k}Z_{k}^{T}v. $$
(4.1)

Lemma 4.1

Suppose that A1–A4 hold. Then, the sequence \((\|\bar{A}_{k}^{+}\| _{2} )_{k\in\mathbb{N}}\) is bounded.

Proof

By A1 and A2, there exists κ 1>0 such that

$$ \|A_{k}\|_{2}\leqslant \kappa_{1},\quad\text{for all}\ k. $$
(4.2)

On the other hand, given \(x\in\mathbb{R}^{m}\), by A4 we have A k x∈span{Z k }, and from Remark 4.1 it follows that

$$\begin{aligned} \|\bar{A}_{k}x\|_{2}^{2} =&\big\| Z_{k}^{T}A_{k}x \big\| _{2}^{2} \\ =& \bigl(Z_{k}^{T}A_{k}x \bigr)^{T} \bigl(Z_{k}^{T}A_{k}x \bigr) \\ =& (A_{k}x )^{T}Z_{k}Z_{k}^{T}A_{k}x \\ =& (A_{k}x )^{T}A_{k}x \\ =&\|A_{k}x\|_{2}^{2}. \end{aligned}$$
(4.3)

Hence,

$$ \|\bar{A}_{k}\|_{2}=\max_{\|x\|_{2}=1}\| \bar{A}_{k}x\|_{2}=\max_{\|x\| _{2}=1} \|A_{k}x\|_{2}=\|A_{k}\|_{2}\leqslant \kappa_{1},\quad\text{for all}\ k, $$
(4.4)

and, consequently, there exists κ 2>0 such that

$$ \big\| \bar{A}_{k}^{T}\bar{A}_{k}\big\| _{2}\leqslant \kappa_{2},\quad\text{for all}\ k. $$
(4.5)

Now, since {∇h 1(x k ),⋯,∇h m (x k )}⊂span{Z k }, from Remark 4.1 it follows that

$$ A_{k}=Z_{k}Z_{k}^{T}A_{k}. $$
(4.6)

Thus,

$$ \bar{A}_{k}^{T}\bar {A}_{k}= \bigl(Z_{k}^{T}A_{k}\bigr)^{T} \bigl(Z_{k}^{T}A_{k}\bigr)=A_{k}^{T}Z_{k}Z_{k}^{T}A_{k}=A_{k}^{T}A_{k}, $$
(4.7)

and, by A3, the matrix \(\bar{A}_{k}^{T}\bar{A}_{k}\) is invertible. This implies that \(\bar{A}_{k}\) has full column rank and, therefore,

$$ \bar{A}_{k}^{+}=\bigl(\bar{A}_{k}^{T} \bar{A}_{k}\bigr)^{-1}\bar{A}_{k}^{T}. $$
(4.8)

Let \(\mathit{GL}(n,\mathbb{R})\) be the set of n×n invertible matrices of real numbers. It is well known that the matrix inversion \(\varphi :\mathit{GL}(n,\mathbb{R})\rightarrow \mathit{GL}(n,\mathbb{R})\) defined by φ(M)=M −1 is a continuous function (see, e.g., Theorem 2.3.4 in Golub and Van Loan [6]). Hence, by (4.5), there exists κ 3>0 such that

$$ \big\| \bigl(\bar{A}_{k}^{T}\bar{A}_{k} \bigr)^{-1}\big\| \leqslant \kappa_{3},\quad\text{for all}\ k. $$
(4.9)

Finally, by (4.8), (4.9), and (4.4), there exists κ 4>0 such that

$$ \big\| \bar{A}_{k}^{+}\big\| \leqslant \kappa_{4},\quad\text{for all}\ k, $$
(4.10)

and the proof is complete. □

Lemma 4.2

The inequality

$$ \|c_{k}\|_{2}-\big\| c_{k}+A_{k}^{T}s_{k} \big\| _{2}\geqslant \min \biggl\{ \|c_{k}\| _{2}, \frac{b_{2}\varDelta_{k}}{\|\bar{A}_{k}^{+}\|_{2}} \biggr\} $$
(4.11)

holds for all k, where b 2 is introduced in (1.9).

Proof

By following the same argument as in the proof of Lemma 3.3 in Powell and Yuan [11], we conclude that the inequality

$$ \|c_{k}\|_{2}-\big\| c_{k}+\bar{A}_{k}^{T} \bar{s}_{k}\big\| _{2}\geqslant \min \biggl\{ \| c_{k} \|_{2},\frac{b_{2}\varDelta_{k}}{\|\bar{A}_{k}^{+}\|_{2}} \biggr\} $$
(4.12)

holds for all k. Since \(s_{k}=Z_{k}\bar{s}_{k}\in\mathrm{span} \{ Z_{k} \}\), it follows from Remark 4.1 that \(s_{k}=Z_{k}Z_{k}^{T}s_{k}\), and then

$$ \bar{A}_{k}^{T}\bar{s}_{k}= \bigl(Z_{k}^{T}A_{k} \bigr)^{T}Z_{k}^{T}s_{k}=A_{k}^{T}Z_{k}Z_{k}^{T}s_{k}=A_{k}^{T}s_{k}. $$
(4.13)

Now, by replacing (4.13) in (4.12) we obtain (4.11). □

Lemma 4.3

There exists a positive constant m 1 such that the inequality

$$\begin{aligned} &D_{k}+\frac{1}{2}\mu_{k} \bigl(\|c_{k} \|_{2}^{2}-\big\| c_{k}+A_{k}^{T}s_{k} \big\| _{2}^{2} \bigr) \\ &\quad \leqslant -\frac{1}{4}\big\| P_{k}g_{k}^{*} \big\| _{2}^{2}\min \biggl\{ \frac{1}{2\|\bar {B}_{k}\|_{2}},\frac{\varDelta_{k}^{*}}{\|P_{k}g_{k}^{*}\|_{2}} \biggr\} +m_{1}\|s_{k}\|_{2}\|c_{k} \|_{2} \\ &\qquad{}-\frac{1}{2}\mu_{k}\|c_{k}\|_{2}\min \biggl\{ \|c_{k}\|_{2},\frac {b_{2}\varDelta_{k}}{\|\bar{A}_{k}^{+}\|_{2}} \biggr\} \end{aligned}$$
(4.14)

holds for all k, where D k is given by (1.12) and we use the notation

$$\begin{aligned} g_{k}^{*} =&g_{k}+B_{k}s_{k}^{*}, \end{aligned}$$
(4.15)
$$\begin{aligned} \varDelta_{k}^{*} =& \bigl(\varDelta_{k}^{2}- \big\| s_{k}^{*}\big\| _{2}^{2} \bigr)^{\frac{1}{2}}, \end{aligned}$$
(4.16)
$$\begin{aligned} s_{k}^{*} =& (I_{n}-P_{k} )s_{k}, \end{aligned}$$
(4.17)
$$\begin{aligned} P_{k} =& I_{n}-A_{k}A_{k}^{+}. \end{aligned}$$
(4.18)

Proof

By following the same argument as in the proof of Lemma 3.4 in Powell and Yuan [11], we conclude that there exists a positive constant m 1 for which the inequality

$$\begin{aligned} &\tilde{D}_{k}+\frac{1}{2}\mu_{k} \bigl( \|c_{k}\|_{2}^{2}-\big\| c_{k}+\bar {A}_{k}^{T}\bar{s}_{k}\big\| _{2}^{2} \bigr) \\ &\quad \leqslant -\frac{1}{4}\|\tilde{P}_{k}\tilde{g}_{k} \|_{2}^{2}\min \biggl\{ \frac{1}{2\|\bar{B}_{k}\|_{2}},\frac{\tilde{\varDelta}_{k}}{\|\tilde {P}_{k}\tilde{g}_{k}\|_{2}} \biggr\} +m_{1}\|\bar{s}_{k}\|_{2} \|c_{k}\| _{2} \\ &\qquad{}-\frac{1}{2}\mu_{k}\|c_{k}\|_{2}\min \biggl\{ \|c_{k}\|_{2},\frac {b_{2}\varDelta_{k}}{\|\bar{A}_{k}^{+}\|_{2}} \biggr\} \end{aligned}$$
(4.19)

holds for all k, where

$$\begin{aligned} \tilde{D}_{k} =& (\bar{g}_{k}-\bar{A}_{k}\bar{ \lambda}_{k} )^{T}\bar{s}_{k}+\frac{1}{2} \bar{s}_{k}^{T}\bar{B}_{k}\check {s}_{k}- [\bar{\lambda}_{k+1}-\bar{\lambda}_{k} ]^{T}\biggl(c_{k}+\frac{1}{2}\bar{A}_{k}^{T} \bar{s}_{k}\biggr) \\ &{}+\mu_{k} \bigl(\big\| c_{k}+\bar{A}_{k}^{T} \bar{s}_{k}\big\| _{2}^{2}-\|c_{k}\| _{2}^{2} \bigr), \end{aligned}$$
(4.20)
$$\begin{aligned} \bar{\lambda}_{k} =&\bar{A}_{k}^{+} \bar{g}_{k}, \end{aligned}$$
(4.21)
$$\begin{aligned} \check{s}_{k} =&\tilde{P}_{k}\bar{s}_{k}, \end{aligned}$$
(4.22)
$$\begin{aligned} \tilde{P}_{k} =&I_{r_{k}}-\bar{A}_{k} \bar{A}_{k}^{+}, \end{aligned}$$
(4.23)
$$\begin{aligned} \tilde{g}_{k} =&\bar{g}_{k}+\bar{B}_{k} \tilde{s}_{k}, \end{aligned}$$
(4.24)
$$\begin{aligned} \tilde{\varDelta}_{k} =& \bigl(\varDelta_{k}^{2}-\| \tilde{s}_{k}\| _{2}^{2} \bigr)^{\frac{1}{2}}, \end{aligned}$$
(4.25)
$$\begin{aligned} \tilde{s}_{k} =& (I_{r_{k}}-\tilde{P}_{k} ) \bar{s}_{k}. \end{aligned}$$
(4.26)

From (4.13) we have

$$ \big\| c_{k}+\bar{A}_{k}^{T}\bar{s}_{k}\big\| _2= \big\| c_{k}+A_{k}^{T}s_{k}\big\| _{2}. $$
(4.27)

We shall prove that

$$ \tilde{D}_{k}=D_{k},\qquad\tilde{\varDelta}_{k}= \varDelta_{k}^{*},\qquad\big\| \tilde {P}_{k}\tilde{g}_{k} \big\| _{2}=\big\| P_{k}g_{k}^{*} \big\| _{2},\quad\text{and}\quad \|\bar{s}_{k}\|_{2}= \|s_{k}\|_{2}. $$
(4.28)

Then, (4.14) will follow directly from (4.19). Since \(s_{k}=Z_{k}\bar{s}_{k}\) and g k belong to span{Z k }, from Remark 4.1 it follows that

$$\begin{aligned} s_{k} =&Z_{k}Z_{k}^{T}s_{k}, \end{aligned}$$
(4.29)
$$\begin{aligned} g_{k} =&Z_{k}Z_{k}^{T}g_{k}. \end{aligned}$$
(4.30)

Moreover, recalling the definitions of \(g_{k}^{*}\), \(s_{k}^{*}\), \(\hat{s}_{k}\) and P k (in (4.15), (4.17), (1.13) and (4.18), respectively) and assumption A4, we see that \(\{g_{k}^{*},s_{k}^{*},\hat{s}_{k},P_{k}g_{k}^{*} \}\subset \mathrm{span} \{Z_{k} \}\). Consequently, by Remark 4.1,

$$\begin{aligned} g_{k}^{*} =&Z_{k}Z_{k}^{T}g_{k}^{*}, \end{aligned}$$
(4.31)
$$\begin{aligned} s_{k}^{*} =&Z_{k}Z_{k}^{T}s_{k}^{*}, \end{aligned}$$
(4.32)
$$\begin{aligned} \hat{s}_{k} =&Z_{k}Z_{k}^{T} \hat{s}_{k}, \end{aligned}$$
(4.33)
$$\begin{aligned} P_{k}g_{k}^{*} =&Z_{k}Z_{k}^{T}P_{k}g_{k}^{*}. \end{aligned}$$
(4.34)

From (4.21), (4.8), (4.7), and (4.30), it follows that

$$\begin{aligned} \bar{\lambda}_{k} =&\bar{A}_{k}^{+} \bar{g}_{k} \\ =& \bigl(\bar{A}_{k}^{T}\bar{A}_{k} \bigr)^{-1}\bar{A}_{k}^{T}\bar {g}_{k} \\ =& \bigl(A_{k}^{T}A_{k} \bigr)^{-1}A_{k}^{T}Z_{k}Z_{k}^{T}g_{k} \\ =& \bigl(A_{k}^{T}A_{k} \bigr)^{-1}A_{k}^{T}g_{k} \\ =&A_{k}^{+}g_{k} \\ =&\lambda_{k}. \end{aligned}$$
(4.35)

By (4.35) and (4.29) we obtain

$$\begin{aligned} (\bar{g}_{k}-\bar{A}_{k}\bar{\lambda}_{k} )^{T}\bar {s}_{k} =& \bigl(Z_{k}^{T}g_{k}-Z_{k}^{T}A_{k} \lambda_{k} \bigr)^{T}Z_{k}^{T}s_{k} \\ =& (g_{k}-A_{k}\lambda_{k} )^{T}Z_{k}Z_{k}^{T}s_{k} \\ =& (g_{k}-A_{k}\lambda_{k} )^{T}s_{k}. \end{aligned}$$
(4.36)

Further, by (4.22), (4.23), (4.8), (4.7), (4.29), and (1.13),

$$\begin{aligned} \check{s}_{k} =&\tilde{P}_{k}\bar{s}_{k} \\ =& \bigl(I_{r_{k}}-\bar{A}_{k}\bar{A}_{k}^{+} \bigr) \bar{s}_{k} \\ =&\bar{s}_{k}-\bar{A}_{k} \bigl(\bar{A}_{k}^{T} \bar{A}_{k} \bigr)^{-1}\bar{A}_{k}^{T} \bar{s}_{k} \\ =&Z_{k}^{T}s_{k}-Z_{k}^{T}A_{k} \bigl(A_{k}^{T}A_{k} \bigr)^{-1}A_{k}^{T}Z_{k} \bar{s}_{k} \\ =&Z_{k}^{T} \bigl(s_{k}-A_{k} \bigl(A_{k}^{T}A_{k} \bigr)^{-1}A_{k}^{T}s_{k} \bigr) \\ =&Z_{k}^{T} \bigl[ \bigl(I_{n}-A_{k}A_{k}^{+} \bigr)s_{k} \bigr] \\ =&Z_{k}^{T}P_{k}s_{k} \\ =&Z_{k}^{T}\hat{s}_{k}. \end{aligned}$$
(4.37)

Note that the equalities (4.37), (4.29), and (4.33) imply that

$$\begin{aligned} \bar{s}_{k}^{T}\bar{B}_{k}\check{s}_{k} =& \bar{s}_{k}\bar {B}_{k}Z_{k}^{T} \hat{s}_{k} \\ =& (Z_{k}^Ts_{k} )^{T} \bigl(Z_{k}^{T}B_{k}Z_{k} \bigr)Z_{k}^{T}\hat{s}_{k} \\ =& \bigl(s_{k}^{T}Z_{k}Z_{k}^{T} \bigr)B_{k} \bigl(Z_{k}Z_{k}^{T}\hat {s}_{k} \bigr) \\ =& \bigl(Z_{k}Z_{k}^{T}s_{k} \bigr)^{T}B_{k} \bigl(Z_{k}Z_{k}^{T} \hat {s}_{k} \bigr) \\ =&s_{k}^{T}B_{k}\hat{s}_{k}. \end{aligned}$$
(4.38)

Now, by (4.36), (4.38), (4.35), (4.13), and (4.27), we conclude that

$$ \tilde{D}_{k}=D_{k}. $$
(4.39)

From (4.26), (4.23), (4.8), (4.7), (4.29), (4.18), and (4.17) it follows that

$$\begin{aligned} \tilde{s}_{k} =&\bar{A}_{k}\bar{A}_{k}^{+} \bar{s}_{k} \\ =&\bar{A}_{k} \bigl(\bar{A}_{k}^{T} \bar{A}_{k} \bigr)^{-1}\bar {A}_{k}^{T} \bar{s}_{k} \\ =&Z_{k}^{T}A_{k} \bigl(A_{k}^{T}A_{k} \bigr)^{-1}A_{k}^{T}Z_{k}Z_{k}^{T}s_{k} \\ =&Z_{k}^{T}A_{k} \bigl(A_{k}^{T}A_{k} \bigr)^{-1}A_{k}^Ts_{k} \\ =&Z_{k}^{T}A_{k}A_{k}^{+}s_{k} \\ =&Z_{k}^{T} \bigl[ (I_{n}-P_{k} )s_{k} \bigr] \\ =&Z_{k}^{T}s_{k}^{*}. \end{aligned}$$
(4.40)

Then, by (4.32),

$$ \|\tilde{s}_{k}\|_{2}^{2}=\big\| Z_{k}^{T}s_{k}^{*} \big\| _{2}^{2}= \bigl(s_{k}^{*} \bigr)^{T}Z_{k}Z_{k}^{T}s_{k}^{*}= \bigl(s_{k}^{*} \bigr)^{T}s_{k}^{*}= \big\| s_{k}^{*}\big\| _{2}^{2}, $$
(4.41)

which implies that

$$ \tilde{\varDelta}_{k}= \bigl(\varDelta_{k}^{2}-\| \tilde{s}_{k}\|_{2}^{2} \bigr)^{\frac{1}{2}}= \bigl(\varDelta_{k}^{2}-\big\| s_{k}^{*} \big\| _{2}^{2} \bigr)^{\frac {1}{2}}=\varDelta_{k}^{*}. $$
(4.42)

On the other hand, from (4.24), (4.40), (4.32), and (4.15) it follows that

$$\begin{aligned} \tilde{g}_{k} =&\bar{g}_{k}+\bar{B}_{k} \tilde{s}_{k} \\ =&Z_{k}^{T}g_{k}+Z_{k}^{T}B_{k}Z_{k}Z_{k}^{T}s_{k}^{*} \\ =&Z_{k}^{T} \bigl(g_{k}+B_{k}s_{k}^{*} \bigr) \\ =&Z_{k}^{T}g_{k}^{*}. \end{aligned}$$
(4.43)

Thus, by (4.23), (4.8), (4.7), (4.31), and (4.18),

$$\begin{aligned} \tilde{P}_{k}\tilde{g}_{k} =& \bigl(I_{r_{k}}- \bar{A}_{k}\bar {A}_{k}^{+} \bigr) \tilde{g}_{k} \\ =& \bigl(I_{r_{k}}-Z_{k}^{T}A_{k} \bigl(A_{k}^{T}A_{k} \bigr)^{-1}A_{k}^{T}Z_{k} \bigr)Z_{k}^{T}g_{k}^{*} \\ =&Z_{k}^{T} \bigl[g_{k}^{*}-A_{k}A_{k}^{+}g_{k}^{*} \bigr] \\ =&Z_{k}^{T}P_{k}g_{k}^{*}. \end{aligned}$$
(4.44)

Now, equalities (4.44) and (4.34) imply that

$$\begin{aligned} \|\tilde{P}_{k}\tilde{g}_{k}\|_{2}^{2} =& \big\| Z_{k}^{T}P_{k}g_{k}^{*}\big\| _{2}^{2} \\ =& \bigl(P_{k}g_{k}^{*} \bigr)^{T}Z_{k}Z_{k}^{T}P_{k}g_{k}^{*} \\ =& \bigl(P_{k}g_{k}^{*} \bigr)^{T} \bigl(P_{k}g_{k}^{*} \bigr) \\ =&\big\| P_{k}g_{k}^{*}\big\| _{2}^{2} \end{aligned}$$
$$ \quad\Longrightarrow\quad\|\tilde{P}_{k}\tilde{g}_{k} \|_{2}=\big\| P_{k}g_{k}^{*} \big\| _{2}. $$
(4.45)

Finally, by (4.29),

$$\begin{aligned} &\|\bar{s}_{k}\|_{2}^{2}=\big\| Z_{k}^{T}s_{k} \big\| _{2}^{2}=s_{k}^{T}Z_{k}Z_{k}^{T}s_{k}=s_{k}^{T}s_{k}= \|s_{k}\|_{2}^{2} \\ &\quad\Longrightarrow\quad\|\bar{s}_{k}\|_2=\|s_{k}\|_2. \end{aligned}$$
(4.46)

Hence, by (4.39), (4.27), (4.45), (4.42), and (4.46), the inequality (4.19) reduces to the inequality (4.14) and the proof is complete. □

Theorem 4.1

Suppose that A1–A5 hold. Then, Algorithm 3.1 will terminate after finitely many iterations. In other words, if we remove the convergence test from Step 1, then s k =0 for some k or the limit

$$ \liminf_{k\to\infty} \bigl[\|c_{k}\|_{2}+ \|P_{k}g_{k}\|_{2} \bigr]=0 $$
(4.47)

is obtained, which ensures that {x k } is not bounded away from stationary points of the problem (1.1)–(1.2).

Proof

It follows from Lemmas 4.1, 4.2 and 4.3 by the same argument as in Powell and Yuan [11]. □

Remark 4.2

By Theorem 4.1, the Algorithm 3.1 is globally convergent for any subspace S k =span{Z k } such that Z k satisfies A4.

5 Numerical Results

In order to investigate the proposed algorithm from a computational point of view, and to explore its potentialities and limitations, we have tested MATLAB implementations of Algorithms 1.1 and 3.1 on a set of 50 problems from CUTEr collection [8]. The dimension of the problems varies from 3 to 1498, while the number of constraints are between 1 and 96. Here, we refer to our implementations of Algorithms 1.1 and 3.1 as “PYtr” and “SPYtr”, respectively. No attempt is made to compare either of the codes with other solvers.

In both implementations, the CDT subproblem is solved by the dual algorithm proposed by Yuan [16], with the parameters s 0=1, υ=0.001 and ε=10−12. In this algorithm, instead of update M k by the rule

$$ M_{k}=\max \bigl\{ M_{k-1},d^{T}H^{-1}d+y^{T}H^{-1}y \bigr\} , $$

we use

$$ M_{k}=d^{T}H^{-1}d+y^{T}H^{-1}y, $$

since the latter rule allowed a faster convergence in the numerical tests (see Algorithm 3.1 in [16]). Moreover, the maximum number of iterations for this algorithm was fixed as 200.

To find a value of ξ k in the interval (1.9), the LSQI problem

$$\begin{aligned} &\min \big\| c_{k}+A_{k}^{T}d\big\| _{2}, \\ &\text{s.t.}\quad \|d\|_{2}\leqslant b_{1}\varDelta_{k}, \end{aligned}$$

is solved by Algorithm 12.1.1 described in Golub and Van Loan [6], which provides a solution d k . Then, ξ k is taken as

$$ \xi_{k}=\big\| c_{k}+A_{k}^{T}d_{k} \big\| _{2}. $$

For both implementations, the parameters in Step 0 are chosen as Δ 1=1, ε s =10−4, μ 1=1, γ=10−8 and b 1=b 2=0.9. Therefore, each implementation was terminated when ∥c k ∥2+∥g k −A k λ k ∥2⩽10−4. The initial matrix B 1 is chosen as the identity matrix and B k is updated by the damped BFGS formula of Powell [10], namely

$$ B_{k+1}=B_{k}-\frac {B_{k}s_{k}s_{k}^{T}B_{k}}{s_{k}^{T}B_{k}s_{k}}+\frac{\eta_{k}\eta _{k}^{T}}{s_{k}^{T}\eta_{k}}, $$

where

$$ s_{k}=x_{k+1}-x_{k},\qquad\eta_{k}= \theta_{k}y_{k}+(1-\theta_{k})B_{k}s_{k}, $$

and

$$ \theta_{k}=\left \{ \begin{array}{l@{\quad}l} 1, & \text{if}\ s_{k}^{T}y_{k}\geqslant 0.2s_{k}^{T}B_{k}s_{k}\\ 0.8s_{k}^{T}B_{k}s_{k}/ [s_{k}^{T}B_{k}s_{k}-s_{k}^{T}y_{k} ],& \text{otherwise}. \end{array} \right . $$

The algorithms were coded in MATLAB language, and the tests were performed with MATLAB 7.8.0 (R2009a), on an PC with a 2.53 GHz Intel(R) i3 microprocessor, and using a Ubunto virtual machine with memory limited to 896 MB.

Problems and results are given in Table 1, where “Itr” represents the number of iterations, “Time” represents the CPU time (in seconds), “n” represents the number of variables, “m” represents the number of constraints, and an entry “F” indicates that the code stopped due some error during the solution of the CDT subproblem. The asterisk indicates that the original CUTEr problem has been modified for our case, for example, inequalities constraints may have been considered as equalities, or the bounds on the variables may have been ignored. We report only the number of iterations Itr because the number of evaluations of f(x), c(x), g(x) and A(x) is equal to Itr+1 in both algorithms. For each problem in which both codes were successful, the optimal objective function values obtained were the same.

Table 1 Numerical results for CUTEr problems
Full size table

To facilitate comparison between the two algorithms, we use the performance profile proposed by Dolan and Moré [4]. This tool for benchmarking and comparing optimization softwares works in the following way. Let t p,s denote the time to solve problem p by solver s. The performance ratio is defined as

$$ r_{p,s}=\frac{t_{p,s}}{t_{p}^{*}}, $$

where \(t_{p}^{*}\) is the lowest time required by any solver to solve problem p. Therefore, r p,s ⩾1 for all p and s. If a solver does not solve a problem, the ratio r p,s is assigned a large number r M , which satisfies r p,s <r M for all p,s where solver s succeeds in solving problem p. The performance profile for each code s is defined as the cumulative distribution function for the performance ratio r p,s , which is

$$ \rho_{s}(\tau)=\frac{\text{no. of problems s.t. $r_{p,s}\leqslant \tau $}}{\text{total no. of problems}}. $$

If τ=1, then ρ s (1) represents the percentage of problems for which the solver s’s runtime is the best. The performance profile can also be used to analyze the number of iterations required to satisfy the stopping criteria.

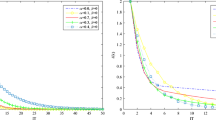
Based on the numerical results in Table 1, we give the performance profile for the codes PYtr and SPYtr considering two distinct subsets of problems. The first one corresponds to the first 35 problems in Table 1 (for which n<10), while the second subset corresponds to the remaining 15 problems (for which n⩾10). The performance profiles in Fig. 1 for the first subset of problems show that PYtr is slightly more efficient than SPYtr with respect to the number of iterations and the computational time required to reduce the stationarity measure below ε s . Regarding the computational time, this result is not surprising, since in the problems considered the gap between n and m is very small. In this case, the trial step is computed on the subspaces only in very few iterations, and the time saved in this computation is not enough to compensate the time consumed in the reorthogonalization procedure.

Fig. 1
figure 1

Performance profiles for problems with n<10

Full size image

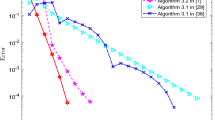
On the other hand, the performance profiles in Fig. 2 show a different picture for the second subset of problems, which includes medium size instances where n≫m. For these problems, both codes require almost the same number of iterations, but SPYtr is significantly faster than PYtr.

Fig. 2
figure 2

Performance profiles for problems with n⩾10

Full size image

6 Conclusion and Future Research

Based on subspace properties of the CDT subproblem, we have presented a subspace version of the Powell–Yuan trust-region algorithm for equality constrained optimization. Under suitable conditions, the new algorithm is proved to be globally convergent. Preliminary numerical experiments indicate that the subspace algorithm outperforms its “full space” counterpart on problems where the number of constraints is much lower than the number of variables. Future research include the conducting of extensive numerical tests using more sophisticated implementations, and the development of a strategy to control the size of the subspaces, similar that one proposed by Gong [7] for unconstrained optimization. Further, it is worth to mention that the subspace properties of the CDT subproblem derived in this work can be used to develop subspace versions of any algorithm based on the CDT subproblem, such as the algorithm of Celis, Dennis and Tapia [2].