1 Introduction

1.1 What is Compressive Sensing?

The flows of data (e.g., signals and images) around us are enormous today and rapidly growing. However, the number of salient features hidden in massive data are usually much smaller than the number of coefficients in a standard representation of the data. Hence data are compressible. In data processing, the traditional practice is to measure (sense) data in full length and then compress the resulting measurements before storage or transmission. In such a scheme, recovery of data is generally straightforward. This traditional data-acquisition process can be described as “full sensing plus compressing”. Compressive sensing (CS), also known as compressed sensing or compressive sampling, represents a paradigm shift in which the number of measurements is reduced during acquisition so that no additional compression is necessary. The price to pay is that more sophisticated recovery procedures become necessary.

In this paper, we will use the term “signal” to represent generic data (so an image is a signal). Let \(\bar{x}\in\mathbb{R}^{n}\) represent a discrete signal and \(b \in\mathbb{R}^{m}\) a vector of linear measurements formed by taking inner products of \(\bar{x}\) with a set of linearly independent vectors \(a_{i} \in\mathbb{R}^{n}\), i=1,2,⋯,m. In matrix format, the measurement vector is \(b =A\bar{x}\), where \(A \in\mathbb{R}^{m \times n}\) has rows \(a_{i}^{T}\), i=1,2,⋯,m. This process of obtaining b from an unknown signal \(\bar{x}\) is often called encoding, while the process of recovering \(\bar{x}\) from the measurement vector b is called decoding.

When the number of measurements m is equal to n, decoding simply entails solving a linear system of equations, i.e., \(\bar{x}= A^{-1}b\). However, in many applications, it is much more desirable to take fewer measurements provided one can still recover the signal. When m<n, the linear system Ax=b is typically under-determined, permitting infinitely many solutions. In this case, is it still possible to recover \(\bar{x}\) from b through a computationally tractable procedure?

If we know that the measurement b is from a highly sparse signal (i.e., it has very few nonzero components), then a reasonable decoding model is to look for the sparsest signal among all those that produce the measurement b; that is,

$$ \min\bigl\{\|x\|_0: Ax=b\bigr\}, $$
(1.1)

where the quantity ∥x∥0 denotes the number of non-zeros in x. Model (1.1) is a combinatorial optimization problem with a prohibitive complexity if solved by enumeration, and thus does not appear tractable. An alternative model is to replace the “ℓ 0-norm” by the ℓ 1-norm and solve a computationally tractable linear program:

$$ \min\bigl\{\|x\|_1: Ax=b\bigr\}. $$
(1.2)

This approach, often called basis pursuit, was popularized by Chen, Donoho and Sauders [9] in signal processing, though similar ideas existed earlier in other areas such as geo-sciences (see Santosa and Symes [27], for example).

In most applications, sparsity is hidden in a signal \(\bar{x}\) so that it becomes sparse only under a “sparsifying” basis Φ; that is, \(\varPhi\bar{x}\) is sparse instead of \(\bar{x}\) itself. In this case, one can do a change of variables z=Φx and replace the equation Ax=b by (AΦ −1)z=b. For an orthonormal basis Φ, the null space of AΦ −1 is a rotation of that of A, and such a rotation does not alter the success rate of CS recovery (as we will see later that the probability measure for success or failure is rotation-invariant). For simplicity and without loss of generality, we will assume Φ=I throughout this paper.

Fortunately, under favorable conditions the combinatorial problem (1.1) and the linear program (1.2) can share common solutions. Specifically, if the signal \(\bar{x}\) is sufficiently sparse and the measurement matrix A possesses certain nice attributes (to be specified later), then \(\bar{x}\) will solve both (1.1) and (1.2) for \(b=A\bar{x}\). This property is called recoverability, which, along with the fact that (1.2) can be solved efficiently in theory, establishes the theoretical soundness of the decoding model (1.2).

Generally speaking, compressive sensing refers to the following two-step approach: choosing a measurement matrix \(A\in\mathbb{R}^{m \times n}\) with m<n and taking measurement \(b=A\bar{x}\) on a sparse signal \(\bar{x}\), and then reconstructing \(\bar{x}\in\mathbb{R}^{n}\) from \(b\in\mathbb {R}^{m}\) by some means. Since m<n, the measurement b is already compressed during sensing, hence the name “compressive sensing” or CS. Using the basis pursuit model (1.2) to recover \(\bar{x}\) from b represents a fundamental instance of CS, but certainly not the only one. Other recovery techniques include greedy-type algorithms (see [28], for example).

In this paper, we will exclusively focus on ℓ 1-minimization decoding models, including (1.2) as a special case, because ℓ 1-minimization has the following two advantages: (a) the flexibility to incorporate prior information into decoding models, and (b) uniform recoverability. These two advantages will be introduced and studied in this paper.

1.2 Current Theory for CS via ℓ 1-Minimization

Basic theory of CS presently consists of two components: recoverability and stability. Recoverability addresses the central questions: what types of measurement matrices and recovery procedures ensure exact recovery of all k-sparse signals (those having exactly k-nonzeros) and how many measurements are sufficient to guarantee such a recovery? On the other hand, stability addresses the robustness issues in recovery when measurements are noisy and/or sparsity is inexact.

There are a number of earlier works that have laid the groundwork for the existing CS theory, especially pioneering works by Dohono and his co-workers (see the survey paper [4] for a list of references on these early works). From these early works, it is known that certain matrices can guarantee recovery for sparsity k up to the order of \(\sqrt{m}\) (for example, see Donoho and Elad [12]). In recent seminal works by Candés and Tao [5, 6], it is shown that for a standard normal random matrix \(A\in\mathbb{R}^{m \times n}\), recoverability is ensured with high probability for sparsity k up to the order of m/log(n/m), which is the best recoverability order available. Later the same order has been extended by Baraniuk et al. [1] to a few other random matrices such as Bernoulli matrices with ±1 entries.

In practice, it is almost always the case that either measurements are noisy or signal sparsity is inexact, or both. Here inexact sparsity refers to the situation where a signal contains a small number of significant components in magnitude, while the magnitudes of the rest are small but not necessarily zero. Such approximately sparse signals are compressible too. The subject of CS stability studies the issues concerning how accurately a CS approach can recover signals under these circumstances. Stability results have been established for the ℓ 1-minimization model (1.2) and its extension

$$ \min\bigl\{\|x\|_1: \|Ax-b\|_2 \leqslant \gamma\bigr\}. $$
(1.3)

Consider model (1.2) for \(b=A\hat{x}\) where \(\hat{x}\) is approximately k-sparse so that it has only k significant components. Let \(\hat{x}(k)\) be a so-called (best) k-term approximation of \(\hat {x}\) obtained by setting the n−k insignificant components of \(\hat{x}\) to zero, and let x ∗ be the optimal solution of (1.2). Existing stability results for model (1.2) include the following two types of error bounds,

(1.4)
(1.5)

where the sparsity level k can be up to the order of m/log(n/m) depending on what type of measurement matrices are in use, and C denotes a generic constant independent of dimensions whose value may vary from one place to another. These results are established by Candés and Tao [5] and Candés, Romberg and Tao [7] (see also Donoho [11], and Cohen, Dahmen and DeVore [10]). For the extension model (1.3), the following stability result is obtained by Candés, Romberg and Tao [7]:

$$ \big\|x^*-\hat{x}\big\|_2 \leqslant C\bigl(\gamma+ k^{-1/2}\big\|\hat{x}-\hat{x}(k)\big\|_1\bigr). $$
(1.6)

In the case where \(\hat{x}\) is exactly k-sparse so that \(\hat {x}=\hat{x}(k)\), the above stability results reduce to the exact recoverability: \(x^{*}=\hat{x}\) (also γ=0 is required in (1.6)). Therefore, when combined with relevant random matrix properties, the stability results imply recoverability in the case of solving model (1.2). More recently, stability results have also been established for some greedy algorithms by Needell and Vershynin [25] and Needell and Tropp [24]. Yet, there still exist CS recovery methods that have been shown to possess recoverability but with stability unknown.

Existing results in CS recoverability and stability are mostly based on analyzing properties of the measurement matrix A. The most widely used analytic tool is the so-called Restricted Isometry Property (RIP) of A, first introduced in [6] for the analysis of CS recoverability (but an earlier usage can be found in [21]). Given \(A \in\mathbb{R}^{m \times n}\), the k-th RIP parameter of A, δ k (A), is defined as the smallest quantity δ∈(0,1) that satisfies for some R>0

$$ (1-\delta)R \leqslant \frac{x^TA^TAx}{x^Tx} \leqslant (1+\delta)R, \quad \forall x, \|x\|_0 = k. $$
(1.7)

The smaller δ k (A) is, the better RIP is for that k value. Roughly speaking, RIP measures the “overall conditioning” of the set of m×k submatrices of A (see more discussion below).

All the above stability results (including those in [24, 25]) have been obtained under various assumptions on the RIP parameters of A. For example, the error bounds (1.4) and (1.6) were first obtained under the assumption δ 3k (A)+3δ 4k (A)<2 (which has recently been weakened to \(\delta_{2k}(A) < \sqrt{2}-1\) in [3]). Consequently, stability constants, represented by C above, obtained by existing RIP-based analyses all depend on the RIP parameters of A. We will see, however, that as far as the results within the scope of this paper are concerned, the dependency on RIP can be removed.

Donoho established stable recovery results in [11] under three conditions on measurement matrix A (conditions CS1-CS3). Although these conditions do not directly use RIP properties, they are still matrix-based. For example, condition CS1 requires that the minimum singular values of all m×k sub-matrices, with k<ρm/log(n) for some ρ>0, of \(A \in\mathbb{R}^{m \times n}\) be uniformly bounded below from zero. Consequently, the stability results in [11] are all dependent on matrix A.

Another analytic tool, mostly used by Donoho and his co-authors (for example, see [13]) is to study the combinatorial and geometric properties of the polytope formed by the columns of A. While the RIP approach uses sufficient conditions for recoverability, the “polytope approach” uses a necessary and sufficient condition. Although the latter approach can lead to tighter recoverability constants, the former has so far produced stability results such as (1.4)–(1.6).

1.3 Drawbacks of RIP-based Analyses

In any recovery model using the equation Ax=b, the pair (A,b) carries all the information about the unknown signal. Obviously, Ax=b is equivalent to GAx=Gb for any nonsingular matrix \(G \in\mathbb{R}^{m \times m}\). Numerical considerations aside, (GA,Gb) ought to carry exactly the same amount of information as (A,b) does. However, the RIP properties of A and GA can be vastly different. In fact, one can easily choose G to make the RIP of GA arbitrarily bad no matter how good the RIP of A is.

To see this, let us define

$$ \varGamma_k(A) = \frac{\lambda_{\max}^k}{\lambda_{\min}^k}, \quad \lambda_{\max}^k \triangleq\max_{\|x\|_0=k}\frac{x^TA^TAx}{x^Tx},\quad \lambda_{\min}^k \triangleq\min_{\|x\|_0=k} \frac{x^TA^TAx}{x^Tx}. $$

By equating (1+δ)R to \(\lambda_{\max}^{k}\) and (1−δ)R to \(\lambda_{\min}^{k}\) in (1.7), eliminating R and solving for δ, we obtain an explicit expression for the k-th RIP parameter of A,

$$ \delta_k(A) = \frac{\varGamma_k(A)-1}{\varGamma_k(A)+1}. $$
(1.8)

Without loss of generality, let A=[A 1   A 2] where \(A_{1} \in\mathbb{R}^{m \times m}\) is nonsingular. Set \(G = BA_{1}^{-1}\) for some nonsingular \(B \in\mathbb{R}^{m \times m}\). Then GA=[GA 1   GA 2]=[B   GA 2]. Let \(B_{1} \in \mathbb{R}^{m \times k}\) consist of the first k columns of B and \(\kappa(B_{1}^{T}B_{1})\) be the condition number of \(B_{1}^{T}B_{1}\) in ℓ 2-norm; i.e., \(\kappa(B_{1}^{T}B_{1}) \triangleq\lambda_{1}/\lambda_{k}\) where λ 1 and λ k are, respectively, the maximum and minimum eigenvalues of \(B_{1}^{T}B_{1}\). Then \(\kappa(B_{1}^{T}B_{1}) \leqslant \varGamma_{k}(GA)\) and

$$ \delta_k(GA) \geqslant \frac{\kappa(B_1^TB_1)-1}{\kappa(B_1^TB_1)+1}. $$
(1.9)

Clearly, we can choose B 1 so that \(\kappa(B_{1}^{T}B_{1})\) is arbitrarily large and δ k (GA) is arbitrarily close to one.

Suppose that we try to recover a signal \(\bar{x}\), which is either exactly or approximately sparse, from measurements \(GA\bar{x}\) via solving

$$ \min\bigl\{\|x\|_1: GAx=GA\bar{x}\bigr\} $$
(1.10)

where \(A \in\mathbb{R}^{m \times n}\) is fixed while the row transformation \(G\in\mathbb{R}^{m \times m}\) can be chosen differently (for example, G makes the rows of GA orthonormal). Under the assumption of exact arithmetics, it is obvious that both recoverability and stability should remain exactly the same as long as the row transformation G stays nonsingular. However, since the RIP parameters of GA vary with G, RIP-based results would suggest, misleadingly, that the recoverability and stability of the decoding model (1.10) could vary with G. For example, for any k⩽m/2, if we choose \(\kappa(B_{1}^{T}B_{1}) \geqslant 3\) for \(B_{1} \in\mathbb{R}^{m \times2k}\), then it follows from (1.9) that

$$\delta_{2k}(GA) \geqslant 0.5 > \sqrt{2}-1. $$

Consequently, when applied to (1.10) the RIP-based recoverability and stability results in [3] would fail on any k-sparse signal because the required RIP condition, \(\delta_{2k}(GA) < \sqrt{2}-1\), is violated.

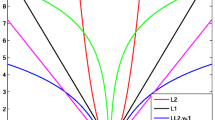
Besides the theoretical drawback discussed above, results from RIP-based analyses are known to be overly conservative in practice. To see this, we present a set of numerical simulations for the cases \(A = [A_{1} \,\, A_{2}] \in\mathbb{R}^{m \times n}\) with \(A_{1} \in\mathbb{R}^{m \times2k}\). A lower bound for δ 2k (A) is

$$ \hat{\delta}_{2k}(A_1) \triangleq \frac{\kappa(A_1^TA_1)-1}{\kappa(A_1^TA_1)+1} \leqslant \delta_{2k}(A), $$
(1.11)

where \(\kappa(A_{1}^{T}A_{1})\) is the condition number (in ℓ 2-norm) of \(A_{1}^{T}A_{1}\). Instead of generating \(A\in\mathbb{R}^{m \times n}\), we randomly sample 500 \(A_{1} \in\mathbb{R}^{m \times2k}\) for each values of m=400,600,800 and \(k = \frac{p}{100}m\) with p=1,2,⋯,10, from either the standard Gaussian or the ±1 Bernoulli distribution. For each random A 1, we calculate \(\hat{\delta}_{2k}(A_{1})\) defined in (1.11) as a lower bound for δ 2k (A) (even though A itself is not generated). The simulation results are presented in Fig. 1. The two pictures show that the behavior of such lower bounds for both Gaussian and Bernoulli distributions is essentially the same. As can be seen from the simulation results, the condition \(\delta_{2k}(A) < \sqrt{2}-1\) required in [3] could possibly hold in reasonable probability only when k/m is below 3 %, which is far below what has generally been observed in practical computations.

Fig. 1
figure 1

Lower bounds for δ 2k (A). The 3 curves depict the mean values of \(\hat{\delta}_{2k}(A_{1})\), as defined in (1.11), from 500 random trials for \(A_{1} \in\mathbb{R}^{m \times2k}\) corresponding to m=400,600,800, respectively, while the error bars indicate their standard deviations. The dotted line corresponds to the value \(\sqrt{2}-1\approx0.414\)

Full size image

1.4 Contributions of this Paper

One contribution of this paper is to develop a non-RIP analysis for the basic theory of CS via ℓ 1-minimization. We derive RIP-free recoverability and stability results that only depend on properties of the null space of A (or GA for that matter) while invariant of matrix representations of the null space. Incidentally, our non-RIP analysis also gives stronger results than those by previous RIP analyses in two aspects described below.

In practice, a priori knowledge often exists about the signal to be recovered. Beside sparsity, existing CS theory does not incorporate such prior-information in decoding models, with the exception of when the signs of a signal are known (see [14, 31], for example). Can we extend the existing theory to explicitly include prior-information into our decoding models? In particular, it is desirable to analyze the following general model:

$$ \min\bigl\{\|x\|_1: \|Ax-b\| \leqslant \gamma, x \in\varOmega\bigr\}, $$
(1.12)

where ∥⋅∥ is a generic norm, γ⩾0 and the set \(\varOmega\subset\mathbb{R}^{n}\) represents prior information about the signal under construction.

So far, different types of measurement matrices have required different analyses, and only a few random matrix types, such as Gaussian and Bernoulli distributions with rather restrictive conditions such as zero mean, have been studied in details. Hence a framework that covers a wide range of measurement matrices becomes highly desirable. Moreover, an intriguing challenge is to show that a large collection of random matrices shares an asymptotic and identical recovery behavior, which appears to be true from empirical observations by different groups (see [15, 16], for example). We will examine this phenomenon that we call uniform recoverability, meaning that recoverability is essentially invariant with respect to different types of random matrices.

In summary, this paper consists of three contributions to the theory of CS via ℓ 1-minimization: (i) an elementary, non-RIP treatment; (ii) a flexible theory that allows any form of prior information to be explicitly included; and (iii) a theoretical explanation of the uniform recoverability phenomenon.

This paper is self-contained, in that it includes derivations for all results, with the exception of invoking two classic results without proofs. To make the paper more accessible to a broad audience while limiting its length, we keep discussions at a minimal level on issues not of immediate relevance, such as historical connections and technical details on some deep mathematical notions.

This paper is not a comprehensive survey on the subject of CS (see [4] for a recent survey on RIP-based CS theory), and does not cover every aspect of CS. In particular, this paper does not discuss in any detail CS applications and algorithms. We refer the reader to the CS resource website at Rice University [32] for more complete and up-to-date information on CS research and practice.

1.5 Notation and Organization

The ℓ 1-norm and the ℓ 2-norm in \(\mathbb{R}^{n}\) are denoted by ∥⋅∥1 and ∥⋅∥2, respectively. For any vector \(v \in \mathbb{R}^{n}\) and α⊂{1,⋯,n}, v α is the sub-vector of v whose elements are indexed by those in α. Scalar operations, such as absolute value, are applied to vectors component-wise. The support of a vector x is denoted as

$$\operatorname{supp}(x) \triangleq\{i: x_i \ne0\}, $$

and \(\|x\|_{0} \triangleq|\operatorname{supp}(x)|\) is the number of non-zeros in x where |⋅| denotes cardinality of a set. For \(\mathcal{F}\subset \mathbb{R}^{n}\) and \(\bar{x}\in\mathbb{R}^{n}\), define \(\mathcal{F}-\bar {x}\triangleq\{x-\bar{x}: x \in\mathcal{F}\}\). For random variables, we use the symbol i.i.d. for the phrase “independently identically distributed”.

This paper is organized as follows. In Sect. 2, we introduce some basic conditions for CS recovery via ℓ 1-minimization. An extended recoverability result is presented in Sect. 3 for standard normal random matrices. Section 4 contains two stability results. We explain the uniform recoverability phenomenon in Sect. 5. Section 6 contains concluding remarks.

2 Sparsest Point and ℓ 1-Minimization

In this section we introduce general conditions that relate finding the sparsest point to ℓ 1-minimization. Given a set \(\mathcal {F}\subset\mathbb{R}^{n}\), we consider the following equivalence relationship:

$$ \mathop{\operatorname{arg}\min}_{x \in\mathcal{F}}\|x \|_0 = \{\bar {x}\} = \mathop{\operatorname{arg}\min}_{x \in\mathcal{F}} \|x\|_{1}. $$
(2.1)

The problem on the left is a combinatorial problem of finding the sparsest point in \(\mathcal{F}\), while the one on the right is a continuous, ℓ 1-minimization problem. The singleton set in the middle indicates that there is a common and unique minimizer \(\bar{x}\) for both problems.

2.1 Preliminaries

For \(A \in\mathbb{R}^{m \times n}\), \(b \in\mathbb{R}^{m}\) and \(\varOmega \subset\mathbb{R}^{n}\), we will study equivalence (2.1) on sets of the form:

$$ \mathcal{F}= \{x: Ax=b\} \cap\varOmega. $$
(2.2)

For any \(\bar{x}\in\mathcal{F}\), the following identity will be useful:

$$ \mathcal{F}-\bar{x}\equiv\mathcal{N}(A)\cap(\varOmega-\bar{x}), $$
(2.3)

where \(\mathcal{N}(A)\) denotes the null space of the matrix A, which can be easily verified as follows:

We start from the following simple but important observation.

Lemma 2.1

Let \(x,y \in\mathbb{R}^{n}\) and \(\alpha=\operatorname{supp}(x)\). A sufficient condition for ∥x∥1<∥y∥1 is

$$ \|y-x\|_1 > 2\big\|(y-x)_\alpha \big\|_1. $$
(2.4)

Moreover, a sufficient condition for ∥x∥ p <∥y∥ p , p=0 and 1, is

$$ \sqrt{\|x\|_0} < \frac{1}{2}\frac{\|y-x\|_1}{\|y-x\|_2}. $$
(2.5)

Proof

Since \(\alpha\,{=}\,\operatorname{supp}(x)\), we have ∥x∥1 = ∥x α ∥1 and x β  = 0 where β = {1,⋯,n} ∖ α. Let y=x+v. We calculate

(2.6)

where in the right-hand side we have added and subtracted the terms ∥x∥1 and ∥v α ∥1. In the above identity, the last term in parentheses is nonnegative due to the triangle inequality:

$$ \|x_\alpha+ v_\alpha\|_1 \geqslant \|x_\alpha\|_1-\|v_\alpha\|_1. $$
(2.7)

Hence, ∥x∥1<∥y∥1 if ∥v β ∥1>∥v α ∥1 which is equivalent to ∥v∥1>2∥v α ∥1. This proves the first part of the lemma. In view of the relationship between the 1-norm and 2-norm,

$$\|v_\alpha\|_1 \leqslant \sqrt{|\alpha|}\|v_\alpha \|_2 \leqslant \sqrt{|\alpha|}\|v\|_2 = \sqrt{\|x \|_0}\|v\|_2. $$

Hence, ∥v∥1>2∥v α ∥1 if \(\|v\|_{1} > 2\sqrt{\|x\|_{0}}\|v\|_{2}\), which proves that (2.5) implies (2.4), hence, ∥x∥1<∥y∥1. Finally, if (2.5) holds, then necessarily

$$ \sqrt{\|y\|_0} \geqslant \frac{1}{2}\frac{\|y-x\|_1}{\|y-x\|_2}. $$
(2.8)

Otherwise, due to the symmetry in the right-hand side of (2.5) or (2.8) with respect to x and y, a contradiction would arise in that ∥x∥1<∥y∥1 and ∥y∥1<∥x∥1. Hence, it follows from (2.5) and (2.8) that ∥x∥0<∥y∥0. This completes the proof. □

Condition (2.5) serves as a nice sufficient condition for an “equivalence” between the two “norms” ∥⋅∥0 and ∥⋅∥1, even though ∥⋅∥0 is not really a norm.

2.2 Sufficient Conditions

We now introduce a sufficient condition, (2.9), for recoverability.

Proposition 2.2

For any \(A \in\mathbb{R}^{m \times n}\), \(b\in\mathbb{R}^{m}\), and \(\varOmega\subset\mathbb{R}^{n}\), equivalence (2.1) holds uniquely at \(\bar{x}\in\mathcal {F}\), where \(\mathcal{F}\) is defined as in (2.2), if the sparsity of \(\bar{x}\) satisfies

$$ \sqrt{\|\bar{x}\|_0} < \min \biggl\{ \frac{1}{2}\frac{\|v\|_1}{\|v\|_2}: v \in\mathcal{N}(A)\cap(\varOmega-\bar{x}) \setminus\{0\} \biggr\}. $$
(2.9)

Proof

Since \(\mathcal{F}\equiv\{\bar{x}+ v: v \in\mathcal{F}-\bar{x}\}\) for any \(\bar{x}\), equivalence (2.1) holds uniquely at \(\bar{x}\in\mathcal {F}\) if and only if

$$ \|\bar{x}+v\|_p > \|\bar{x}\|_p, \quad \forall v \in(\mathcal{F}-\bar{x}) \setminus\{0\}, \quad p = 0, 1. $$
(2.10)

In view of the identity (2.3) and condition (2.5) in Lemma 2.1, (2.9) is clearly a sufficient condition for (2.10) to hold for both p=0 and p=1. □

Remark 1

For \(\varOmega=\mathbb{R}^{n}\), (2.9) reduces to the well-known condition

$$ \sqrt{\|\bar{x}\|_0} < \min \biggl\{ \frac{1}{2}\frac{\|v\|_1}{\|v\|_2}: v \in\mathcal{N}(A)\setminus\{0\} \biggr\}. $$
(2.11)

It is worth noting that for some prior-information set Ω, the right-hand side of (2.9) could be significantly larger than that of (2.11), suggesting that adding prior information can never hurt but potentially help raise the lower bound on recoverable sparsity. Since \(0 \in\mathcal{N}(A)\cap(\varOmega -\bar{x})\) and ∥v∥1/∥v∥2 is scale-invariant, a necessary condition for the right-hand side of (2.9) to be larger than that of (2.11) is that the origin is on the boundary of \(\varOmega-\bar{x}\) (which holds true for the nonnegative orthant, for example).

2.3 A Necessary and Sufficient Condition

For the case \(\varOmega=\mathbb{R}^{n}\), we consider the situation of using a fixed measurement matrix A for the recovery of signals of a fixed sparsity level but all possible values and sparsity patterns.

Proposition 2.3

Given \(A \in\mathbb{R}^{m \times n}\) and any integer k⩾1, the equivalence

$$ \{\bar{x}\} = \mathop{\operatorname{arg}\min}\bigl\{\|x \|_1: Ax=A\bar {x}\bigr\} $$
(2.12)

holds for all \(\bar{x}\in\mathbb{R}^{n}\) such that \(\|\bar{x}\|_{0} \leqslant k\) if and only if

$$ \|v\|_1 > 2\|v_\alpha\|_1, \quad \forall v \in\mathcal{N}(A)\setminus\{0\}, $$
(2.13)

holds for all index sets α⊂{1,⋯,n} such that |α|=k.

Proof

In view of the fact \(\{x: Ax=A\bar{x}\} \equiv\{\bar{x}+ v: v \in \mathcal{N}(A)\}\), (2.12) holds at \(\bar{x}\) if and only if \(\|\bar{x}+v\|_{1} > \|\bar{x}\|_{1}, \forall v \in\mathcal {N}(A)\setminus\{0\}\). As is proved in the first part of Lemma 2.1, (2.13) is a sufficient condition for (2.12) with \(\alpha=\operatorname{supp}(\bar{x})\).

Now we show necessity. Let \(v \in\mathcal{N}(A)\setminus\{0\}\) such that ∥v∥1⩽2∥v α ∥1 for some |α|=k. Choose \(\bar{x}\) such that \(\bar{x}_{\alpha}=-v_{\alpha}\) and \(\bar{x}_{\beta}= 0\) where β complements α in {1,2,⋯,n}. Then \(\|\bar{x}+ v\|_{1} = \|v_{\beta}\|_{1} = \|v\|_{1} - \|v_{\alpha}\|_{1} \leqslant \|v_{\alpha}\|_{1} = \|\bar{x}\|_{1}\), so \(\bar{x}\) is not the unique minimizer of ∥⋅∥1. □

We already know from Proposition 2.2 that if k satisfies

$$ 1 \leqslant \sqrt{k} < \min \biggl\{\frac{1}{2}\frac{\|v\|_1}{\|v\|_2}: v \in \mathcal{N}(A)\setminus\{0\} \biggr\}, $$

then \(\bar{x}\) in (2.12) is also the sparsest point in the set \(\{x: Ax=A\bar{x}\}\).

3 Recoverability

Let us restate the equivalence (2.1) in a more explicit form:

$$ \mathop{\operatorname{arg}\min}_{x \in\varOmega}\bigl\{\|x \|_0: Ax=A\bar {x}\bigr\} = \{\bar{x}\} = \mathop{\operatorname{arg} \min}_{x \in\varOmega}\bigl\{\|x\|_1: Ax=A\bar {x}\bigr\}, $$
(3.1)

where Ω will be assumed to be any nonempty and closed subset of \(\mathbb{R}^{n}\). When Ω is a convex set, the problem on the right-hand side is a convex program that can be efficiently solved at least in theory.

Recoverability addresses conditions under which the equivalence (3.1) holds. The conditions involved include the properties of the measurement matrix A and the degree of sparsity in signal \(\bar{x}\). Clearly, the prior information set Ω can also affect recoverability. However, since we allow Ω to be any subset of \(\mathbb{R}^{n}\), the results we obtain in this paper are the “worst-case” results in terms of varying Ω.

3.1 Kashin-Garnaev-Gluskin Inequality

We will make use of a classic result established in the late 1970’s and early 1980’s by Kashin [21], and Garnaev and Gluskin [17] in a particular form, which provides a lower bound on the ratio of the ℓ 1-norm to the ℓ 2-norm when it is restricted to subspaces of a given dimension. We know that in the entire space \(\mathbb{R}^{n}\), the ratio can vary from 1 to \(\sqrt{n}\), namely,

$$1 \leqslant \frac{\|v\|_1}{\|v\|_2} \leqslant \sqrt{n}, \quad \forall v \in\mathbb{R}^n \setminus\{0\}. $$

Roughly speaking, this ratio is small for sparse vectors that have many zero (or near-zero) elements. However, it turns out that in most subspaces this ratio can have much larger lower bounds than 1. In other words, most subspaces do not contain excessively sparse vectors.

For p<n, let G(n,p) denote the set of all p-dimensional subspaces of \(\mathbb{R}^{n}\) (which is called a Grassmannian). It is known that there exists a unique rotation-invariant probability measure, say Prob(⋅), on G(n,p) (see [23], for example). From our perspective, we will bypass the technical details on how such a probability measure is defined. Instead, it suffices to just mention that drawing a member from G(n,p) uniformly at random amounts to generating an n by p random matrix of i.i.d. entries from the standard normal distribution \(\mathcal{N}(0,1)\) whose range space will be a random member of G(n,p) (see Sect. (3.5) of [2] for a concise introduction).

Theorem 3.1

(Kashin, Garnaev and Gluskin)

For any two natural numbers m<n, there exists a set of (n−m)-dimensional subspaces of \(\mathbb{R}^{n}\), say \(\mathbb{S}\subset\mathbf{G}(n,n-m)\), such that

$$ \mathbf{Prob} (\mathbb{S} ) \geqslant 1-e^{-c_0(n-m)}, $$
(3.2)

and for any \(\mathcal{V}\in\mathbb{S}\),

$$ \frac{\|v\|_1}{\|v\|_2} \geqslant \frac{c_1\sqrt{m}}{\sqrt{1+\log(n/m)}}, \quad\forall v \in \mathcal{V}\setminus\{0\}, $$
(3.3)

where the constants c i >0, i=0,1, are independent of the dimensions.

This theorem ensures that a subspace \(\mathcal{V}\) drawn from G(n,n−m) at random will satisfy inequality (3.3) with high probability when n−m is large. From here on, we will call (3.3) the KGG inequality.

When m<n, the orthogonal complement of each and every member of G(n,m) is a member of G(n,n−m), establishing a one-to-one correspondence between G(n,m) and G(n,n−m). As a result, if \(A \in\mathbb{R}^{m \times n}\) is a random matrix with i.i.d. standard normal entries, then the range space of A T is a uniformly random member of G(n,m), while at the same time the null space of A is a uniformly random member of G(n,n−m) in which the KGG inequality holds with high probability when n−m is large.

Remark 2

Theorem 3.1 contains only a part of the seminal result on the so-called Kolmogorov or Gelfand width in approximation theory, first obtained by Kashin [21] in a weaker form and later improved to the current order by Garnaev and Gluskin [17]. In its original form, the result does not explicitly state the probability estimate, but gives both lower and upper bounds of the same order for the involved Kolmogorov width (see [11] for more information on the Kolmogorov and Gelfand widths and their duality in a case of interest). Theorem 3.1 is formulated after a description given by Gluskin and Milman in [20] (see the paragraph around inequality (5), i.e., the KGG inequality (3.3), on p. 133). As will be seen, this particular form of the KGG result enables a greatly simplified non-RIP CS analysis.

The connections between compressive sensing and the works of Kashin [21] and Garnaev and Gluskin [17] are well known. Candés and Tao [5] used the KGG result to establish that the order of stable recovery is optimal in a sense, though they derived their stable recovery results via an RIP-based analysis. In [11] Donoho pointed out that the KGG result implies an abstract stable recovery result (Theorem 1 in [11] for the case of p=1) in an “indirect manner”. In both cases, the authors used the original form of the KGG result, but in terms of the Gelfand width.

The approach taken in this paper is based on examining the ratio ∥v∥1/∥v∥2 (or a variant of it in the case of uniform recoverability) in the null space of A, while relying on the KGG result in the form of Theorem 3.1 to supply the order of recoverable sparsity and the success probability in a direct manner. This approach was used in [30] to obtain a rather limited recoverability result. In this paper, we also use it to derive stability and uniform recoverability results.

3.2 An Extended Recoverability Result

The following recoverability result follows directly from the sufficient condition (2.9) and the KGG inequality (3.3) for \(\mathcal{V}=\mathcal{N}(A)\) (also see the discussions before and after Theorem 3.1). It extends the result in [6] from \(\varOmega=\mathbb{R}^{n}\) to any \(\varOmega \subset\mathbb{R}^{n}\). We call a random matrix standard normal if it has i.i.d. entries drawn from the standard normal distribution \(\mathcal{N}(0,1)\).

Theorem 3.2

Let m<n, \(\varOmega\subset\mathbb{R}^{n}\), and \(A \in\mathbb{R}^{m \times n}\) be either standard normal or any rank-m matrix such that BA T=0 where \(B \in\mathbb{R}^{(n-m) \times n}\) is standard normal. Then with probability greater than \(1-e^{-c_{0}(n-m)}\), the equivalence (3.1) holds at \(\bar{x}\in\varOmega\) if the sparsity of \(\bar{x}\) satisfies

$$ \|\bar{x}\|_{0} < \frac{c_1^2}{4} \frac{m}{1+\log(n/m)}, $$
(3.4)

where c 0,c 1>0 are some absolute constants independent of the dimensions m and n.

An oft-missed subtlety is that recoverability is entirely dependent on the properties of a subspace but independent of its representations. In Theorem 3.2, we have added a second case for A, where A T can be any basis matrix for the null space of B, to bring attention to this subtle point.

Remark 3

For the case \(\varOmega=\mathbb{R}^{n}\), the sparsity bound given in (3.4) is first established by Candés and Tao [6] for standard normal random matrices. In Baraniuk et al. [1], the same order is extended to a few other random matrices such as Bernoulli matrices whose entries are ±1. Weaker results have been established for partial Fourier and other partial orthonormal matrices with randomly chosen rows by Candés, Romberg and Tao [8], and Rudelson and Vershynin [26]. Moreover, an in-depth study on the asymptotic form for the constant in (3.4) can be found in the work of Donoho and Tanner [13].

We emphasize that in terms of Ω the sparsity order in the right-hand side of (3.4) is a worst-case lower bound for (2.9) since it actually bounds (2.11) from below. In principle, larger lower bounds may exist for (2.9) corresponding to certain prior-information sets \(\varOmega\ne\mathbb{R}^{n}\), though specific investigations will be necessary to obtain such better lower bounds. For Ω equal to the nonnegative orthant of \(\mathbb{R}^{n}\), a better bound has been obtained by Donoho and Tanner [14] (also see [31] for an alternative proof).

3.3 Why is the Extension Useful

The extended recoverability result gives a theoretical guarantee that adding prior information can never hurt but possibly enhance recoverability, which of course is not a surprise. The extended decoding model (1.3) includes many useful variations for the prior information set Ω beside the set \(\varOmega=\{x \in\mathbb{R}^{n}: x\geqslant 0\}\).

For example, consider a two-dimensional image \(\bar{x}\) known to contain blocky regions of almost constant values. In this case, the total variation (TV) of \(\bar{x}\) should be small, which is defined as \({\rm TV}(\bar{x}) \triangleq\sum_{i} \|D_{i}\bar{x}\|_{2}\) where \(D_{i}\bar{x}\in \mathbb{R}^{2}\) is a finite-difference gradient approximation of \(\bar{x}\) evaluated at the pixel i. This prior information is characterized by the set \(\varOmega= \{x: {\rm TV}(x) \leqslant \gamma\}\) for some γ>0, and leads to the decoding model: \(\min\{\|x\|_{1}: Ax=b, {\rm TV}(x) \leqslant \gamma\}\), which, for some appropriate μ>0, is equivalent to

$$ \min\bigl\{\|x\|_1 + \mu{\rm TV}(x): Ax=b\bigr\}. $$
(3.5)

Another form of prior information is that oftentimes a signal \(\bar {x}\) under construction is known to be close to a “prior signal” x p . For example, \(\bar{x}\) is an magnetic resonance image (MRI) taken from a patient today, while x p is the one taken a week earlier from the same person. Given the closeness of the two and assuming both are sparse, we may consider solving the model:

$$ \min\bigl\{\|x\|_1: Ax=b, \|x-x_p \|_1 \leqslant \gamma\bigr\}, $$
(3.6)

which has a prior-information set Ω={x:∥x−x p ∥1⩽γ} for some γ>0. When \(\gamma>\|\bar{x}-x_{p}\|_{1}\), adding the prior information will not raise the lower bound on recoverable sparsity as is given in (2.11), but nevertheless it will still help control errors in recovery, which may arguably be more important in practice.

We first present a numerical experiment based on model (3.5). The left image in Fig. 2 is a grayscale image of 1281×400 pixels with pixel values ranging from 0 (black) to 255 (white). It is supposed to be from full-body magnetic resonance imaging. This image is approximately sparse (the background pixel values are 16 instead of 0 even though the background appears black). Clearly, this image has blocky structures and thus relatively small TV values. This prior information makes model (3.5) suitable. We used a partial Fourier matrix as the measurement matrix A in (3.5), formed by one tenth of the rows of the two-dimensional discrete Fourier matrix. As a result, the measurement vector b consisted of 10 % of the Fourier coefficients of the left image in Fig. 2. These Fourier coefficients were randomly selected but biased towards those associated with lower frequency basis vectors. From these 10 % of the Fourier coefficients, we tried to reconstruct the original image by approximately solving model (3.5) without and with the prior information. The results are the middle and the right images in Fig. 2, corresponding to μ=0 (without the TV term) and μ=10, respectively. The signal-to-noise ratio (SNR) for the middle image is 15.28, while it is 19.89 for the right image. Hence, although the ℓ 1-norm term in (3.5) alone already produced an acceptable recovery quality, the addition of the prior information (the TV term) helped improve the quality significantly.

Fig. 2
figure 2

Simulations of compressive sensing with prior information using model (3.5). The left is the original image, the middle and the right were reconstructed from 10 % of the Fourier coefficients by solving model (3.5) with μ=0 and μ=10, respectively. The SNR of the middle and right images are, respectively, 15.28 and 19.89

Full size image

Since it is sufficient to use 50 % of the complex-valued Fourier coefficients for exactly recovering real images, at least in theory, the use of 10 % of the coefficients represents an 80 % reduction in the amount of data required for recovery. In fact, simulations in this example indicates how CS may be applied to MRI where scanned data are essentially Fourier coefficients of images under construction. A 80 % reduction in MRI scanning time would represent a significant improvement in MRI practice. We refer the reader to the work of Lustig, Donoho, Santos and Pauly [22], and the references therein, for more information on the applications of CS to MRI.

The above example, however, does not show that prior information can actually reduce the number of measurements required for recovery of sparse signals. For that purpose, we present another numerical experiment based on model (3.6) with additional nonnegativity constraint.

We consider reconstructing a nonnegative, sparse signal \(\bar{x}\in\mathbb{R}^{n}\) from the measurement \(b=A\bar{x}\) with or without the prior information that \(\bar{x}\) is close to a known prior signal x p . The decoding models without and with this prior information are, respectively,

(3.7)
(3.8)

In our experiment, the signal length is fixed at n=100, and the sparsity of both \(\bar{x}\) and x p is k=10. More specifically, both \(\bar {x}\) and x p have 10 nonzero elements of the value 1, but only 8 of the 10 nonzero positions coincide while the other 2 nonzeros occur at different positions. Roughly speaking, there is a 20 % difference between \(\bar{x}\) and x p . Obviously, \(\|\bar{x}-x_{p}\|_{1}=4\).

We ran both (3.7) and (3.8) on 100 random problems with the number of measurements m=2,4,⋯,40, where in each problem \(A \in\mathbb{R}^{m \times n}\) is a standard Gaussian random matrix, and the 10 nonzero positions of \(\bar{x}\) and x p are randomly chosen with 8 positions coinciding. In (3.8), we set γ=4 which equals \(\|\bar{x}-x_{p}\|_{1}\) by construction. We regard a recovered signal to be “exact” if it has a relative error below 10−4. The numerical results are presented in Fig. 3 that gives the percentage of exact recovery and the average relative error in ℓ 2-norm on 100 random trials for each m value.

Fig. 3
figure 3

Recovery rate (left) and average relative error (right) on 100 random problems with (solid line) and without (dashed line) prior information. For fixed n=100 and k=10, the number of measurements m ranges from 2 to 40

Full size image

We observe that without the prior information m=40 was needed for 100-percent recovery, while with the prior information m=20 was enough. If we consider approximate recovery, we see that to achieve an accuracy with relative errors below 10-percent, the required numbers of measurements were m=30 and m=14, respectively, for models (3.7) and (3.8).

4 Stability

In practice, a measurement vector b is most likely inaccurate due to various sources of imprecisions and/or contaminations. A more realistic measurement model should be \(b=A\bar{x}+r\) where \(\bar{x}\) is a desirable and sparse signal, and \(r \in\mathbb{R}^{m}\) can be interpreted either as noise or as spurious measurements generated by a noise-like signal. Now given an under-sampled and imprecise measurement vector \(b=A\bar{x}+r\), can we still approximately recover the sparse signal \(\bar{x}\)? What kind of errors should we expect? These are questions our stability analysis should address.

4.1 Preliminaries

Assume that \(A \in\mathbb{R}^{m \times n}\) is of rank m and \(b=A\bar{x}+r\), where \(\bar{x}\in\varOmega\subset\mathbb{R}^{n}\). Since the sparse signal of interest, \(\bar{x}\), does not necessarily satisfy the equation Ax=b, we relax our goal to the inequality ∥Ax−b∥⩽γ in some norm ∥⋅∥, with γ⩾∥r∥ so that \(\bar{x}\) satisfies the inequality. An alternative interpretation for the imprecise measurement b is that it is generated by a signal \(\hat{x}\) that is approximately sparse so that \(b=A\hat{x}\) for \(\hat{x}=\bar{x}+p\) where p is small and satisfies Ap=r.

Consider the QR-factorization: A T=UR, where \(U\in\mathbb{R}^{n \times m}\) satisfies U T U=I and \(R \in\mathbb{R}^{m \times m}\) is upper triangular. Obviously, Ax=b is equivalent to U T x=R −T b, and

$$\|Ax-b\|_M=\big\|U^Tx-R^{-T}b\big\|_2, $$

where

$$ \|q\|_M = \bigl(q^TMq \bigr)^{1/2} \quad\mbox{and}\quad M=\bigl(R^TR \bigr)^{-1}. $$
(4.1)

We will make use of the following two projection matrices:

$$ P_r = A^T\bigl(AA^T\bigr)^{-1}A \equiv UU^T \quad\mbox{and}\quad P_n = I - P_r, $$
(4.2)

where P r is the projection onto the range space of A T and P n onto the null space of A. In addition, we will use the constant

$$ C_\nu= \frac{1 + \nu\sqrt{2-\nu^2}}{1-\nu^2} > 1,\quad \nu \in(0,1). $$
(4.3)

It is easy to see that as ν approaches 1, C ν ≈1/(1−ν). For example, C ν ≈2.22 for ν=0.5, C ν ≈4.34 for ν=0.75 and C ν ≈10.43 for ν=0.9.

4.2 Two Stability Results

Given the imprecise measurement \(b=A\bar{x}+r\), consider the decoding model

$$ x_\gamma^* \in\mathop{\operatorname{arg} \min}_{x \in\varOmega}\bigl\{\|x\|_1: \| Ax-b\|_M \leqslant \gamma\bigr\} = \mathop{\operatorname{arg}\min}_{x \in\mathcal{F}(\gamma)} \|x\|_1, $$
(4.4)

where \(\varOmega\subset\mathbb{R}^{n}\) is a closed, prior-information set, γ⩾∥r∥2, the weighted norm is defined in (4.1), and

$$ \mathcal{F}(\gamma) = \bigl\{x: \|Ax-b\|_M \leqslant \gamma, x \in\varOmega\bigr\}. $$
(4.5)

In general, \(x_{\gamma}^{*} \ne\bar{x}\) and is not strictly sparse. We will show that \(x_{\gamma}^{*}\) is close to \(\bar{x}\) under suitable conditions. To our knowledge, stability of this model has not been previously investigated. Our result below says that if \(\mathcal{F}(\gamma)\) contains a sufficiently sparse point \(\bar{x}\), then the distance between \(x_{\gamma}^{*}\) and \(\bar{x}\) is of order γ. Consequently, If \(\bar{x}\in\mathcal{F}(0)\), then \(x_{0}^{*}=\bar{x}\).

The use of the weighted norm ∥⋅∥ M in (4.4) is purely for convenience because it simplifies constants involved in derived results. Had another norm been used, extra constants would appear in some derived inequalities. Nevertheless, due to the equivalence of norms in \(\mathbb{R}^{m}\), the essence of those stability results remains unchanged.

In our stability analysis below, we will make use of the following sparsity condition:

$$ k = \frac{\nu^2}{4} \biggl(\frac{\|u\|_1}{\|u\|_2} \biggr)^2,\quad \mbox{for some } \nu\in(0,1). $$
(4.6)

Theorem 4.1

Let \(\gamma\geqslant \|A\bar{x}-b\|_{M}\) for some \(\bar{x}\in\varOmega\). Assume that \(k=\|\bar{x}\|_{0}\) satisfies (4.6) for \(u=P_{n}(x_{\gamma}^{*}-\bar{x})\) whenever \(P_{n}(x_{\gamma}^{*}-\bar{x}) \ne0\). Then for p=1 or 2

$$ \big\|x_\gamma^*-\bar{x}\big\|_p \leqslant \gamma_p(C_\nu+1) \bigl(\|A\bar{x}-b\| _M+ \gamma\bigr), $$
(4.7)

where \(\gamma_{1}=\sqrt{n}\), γ 2=1 and C ν is defined in (4.3).

Remark 4

We quickly add that if A is a standard normal random matrix, then the KGG inequality (3.3) implies that with high probability the right-hand side of (4.6) for \(u=P_{n}(x_{\gamma}^{*}-\bar {x})\) is at least of the order m/log(n/m). This same comment also applies to the next theorem.

The proof of this theorem, as well as that of Theorem 4.2 below, will be given in Sect. 4.4. Next we consider the special case γ=0, namely,

$$ x_0^*\in\mathop{\operatorname{arg}\min}_{x \in\varOmega}\bigl\{\|x \|_1: Ax=b\bigr\}. $$

A k-term approximation of \(x \in\mathbb{R}^{n}\), denoted by x(k), is obtained from x by setting its n−k smallest elements in magnitude to zero. Obviously, ∥x∥1≡∥x(k)∥1+∥x−x(k)∥1. Due to measurement errors, there may be no sparse signal that satisfies the equation Ax=b. In this case, we show that if the observation b is generated by a signal \(\hat{x}\) that has a good, k-term approximation \(\hat{x}(k)\), then the distance between \(x_{0}^{*}\) and \(\hat{x}\) is bounded by the error in the k-term approximation. Consequently, if \(\hat{x}\) is itself k-sparse so that \(\hat{x}=\hat {x}(k)\), then \(x_{0}^{*}=\hat{x}\).

Theorem 4.2

Let \(\hat{x}\in\varOmega\) satisfy Ax=b and \(\hat{x}(k)\) be a k-term approximation of \(\hat{x}\). Assume that k satisfies

$$ \big\|\hat{x}-\hat{x}(k)\big\|_1\leqslant \|\hat{x} \|_1-\big\|x_0^*\big\|_1 $$
(4.8)

and (4.6) for \(u=P_{n}(x_{0}^{*}-\hat{x}(k))\) whenever \(P_{n}(x_{0}^{*}-\hat{x}(k)) \ne0\). Then for p=1 or 2

$$ \big\|x_0^*-\hat{x}(k)\big\|_p \leqslant (C_\nu+1)\big\|P_r\bigl(\hat{x}-\hat{x}(k)\bigr) \big\|_p, $$
(4.9)

where C ν is defined in (4.3).

It follows from (4.9) and the triangle inequality that for p=1 or 2

$$ \big\|x_0^*-\hat{x}\big\|_p \leqslant (C_\nu+1)\big\|P_r\bigl(\hat{x}-\hat{x}(k)\bigr) \big\|_p + \big\| \hat{x}-\hat{x} (k)\big\|_p, $$
(4.10)

which has the same type of left-hand side as those in (1.4) and (1.5).

Condition (4.8) can always be met for k sufficiently large, while condition (4.6) demands that k be sufficiently small. Together, the two require that the measurement b be observed from a signal \(\hat{x}\) that has a sufficiently good k-term approximation for a sufficiently small k. This requirement seems very reasonable.

4.3 Comparison to RIP-based Stability Results

In the special case of \(\varOmega=\mathbb{R}^{n}\), the error bounds in Theorems 4.1 and 4.2 bear similarities with existing stability results by Candés, Romberg and Tao [7] (see (1.4)–(1.6) in Sect. 1 and also results in [10]), but substantial differences exist in the constants involved and the conditions required. Overall, Theorems 4.1 and 4.2 do not contain, nor are contained in, the existing results, though they all state the same fact that CS recovery based on ℓ 1-minimization is stable to some extent.

The main differences between the RIP-based stability results and ours are reflected in the constants involved. In our error bound (4.9) the constant is given by a formula depending only on the number ν∈(0,1) representing the sparsity level of the signal under construction relative to a maximal recoverable sparsity level. The sparser the signal is, the smaller the constant is, and the more stable the recovery is supposed to be. However, the maximal recoverable sparsity level does depend on the null space of a measurement matrix even though it is independent of matrix representations of that space (hence independent of nonsingular row transformations).

This is not the case, however, with the RIP-based stability results where the involved constants depend on RIP parameters of matrix representations. The smaller the RIP parameters, the smaller those constants. As has been discussed in Sect. 1.3, any RIP-based result, be it recoverability or stability, will unfortunately break down under nonsingular row transformation, even though the decoding model (1.10) itself is mathematically invariant of such a transformation.

Given the monotonicity of the involved stability constants, the key difference between RIP-free and RIP-based stability results can be summarized as follows. For a fixed row space, the former suggests that the sparser is the signal, the more stable; while the latter suggests that the better conditioned is a matrix representation for the row subspace, the more stable. Mathematically, the latter characterization is obviously misleading.

Theorem 4.2 requires a side condition (4.8), which is not required by RIP-based results. We can argue that this side condition is not restrictive because stability results such as (4.9) are only meaningful when the bound on the right-hand side is small; otherwise, the solution errors in the left-hand side would be out of control. Nevertheless, the RIP-free stability result in (4.9) has recently been strengthened by Vavasis [29] who shows that the side condition (4.8) can be removed in the ℓ 1-norm case.

4.4 Proofs of Our Stability Results

Our stability results follow directly from the following simple lemma.

Lemma 4.3

Let \(x,y \in\mathbb{R}^{n}\) such that ∥y∥1⩽∥x∥1, and let y−x=u+w where u T w=0. Whenever u≠0, assume that k=∥x∥0 satisfies (4.6). Then for either p=1 or p=2, there hold

$$ \|u\|_p \leqslant C_\nu\|w\|_p, $$
(4.11)

and

$$ \|y-x\|_p \leqslant (C_\nu+1)\|w \|_p. $$
(4.12)

Proof

If u=0, both (4.11) and (4.12) are trivially true. If u≠0, condition (4.6) and the assumption ∥y∥1⩽∥x∥1 imply that w≠0; otherwise, by Lemma 2.1, (4.6) would imply ∥y∥1>∥x∥1. For u≠0 and w≠0,

$$ \frac{\|u+w\|_1}{\|u+w\|_2} \geqslant \biggl(\frac{1-\|w\|_1/\|u\|_1}{\sqrt{1+(\|w\|_2/\|u\|_2)^2}} \biggr) \frac{\|u\|_1}{\|u\|_2}, $$

which follows from the triangle inequality ∥u+w∥1⩾∥u∥1−∥w∥1. Furthermore,

$$ \frac{\|u+w\|_1}{\|u+w\|_2} \geqslant \biggl(\frac{1-\eta(u,w)}{\sqrt{1+\eta(u,w)^2}} \biggr) \frac{\|u\|_1}{\|u\|_2} \triangleq \phi\bigl(\eta(u,w)\bigr)\frac{\|u\|_1}{\|u\|_2}, $$
(4.13)

where \(\phi(t) = (1-t)/\sqrt{1+t^{2}}\) and

$$ \eta(u,w) \triangleq\max \biggl\{\frac{\|w\|_1}{\|u\|_1}, \frac{\|w\|_2}{\|u\|_2} \biggr\}. $$
(4.14)

If 1−η(u,w)⩽0, then (4.11) trivially holds. Therefore, we assume that η(u,w)<1.

If ϕ(η(u,w))>ν, then it follows from (4.6) and (4.13) that

$$ \sqrt{\|x\|_0} \leqslant \frac{\nu}{2}\frac{\|u\|_1}{\|u\|_2} \leqslant \frac{\nu/\phi(\eta(u,w))}{2}\frac{\|u+w\|_1}{\|u+w\|_2} < \frac{1}{2}\frac{\|u+w\|_1}{\|u+w\|_2}, $$

which would imply ∥x∥1<∥y∥1 by Lemma 2.1, contradicting the assumption of the lemma. Therefore, ϕ(η(u,w))⩽ν must hold. It is easy to verify that

$$\phi(t) = \frac{1-t}{\sqrt{1+t^2}} \leqslant \nu\quad\mbox{and}\quad t < 1 \quad\Longleftrightarrow\quad \frac{1}{C_\nu} \leqslant t < 1, $$

where 1/C ν is the root of the quadratic q(t)≜(1−t)2−ν 2(1+t 2) that is smaller than 1 (noting that ϕ(t)⩽ν is equivalent to q(t)⩽0 for t<1). We conclude that there must hold η(u,w)⩾1/C ν , which implies (4.11) in view of the definition of η(u,w) in (4.14). Finally, (4.12) follows directly from the relationship y−x=u+w, the triangle inequality, and (4.11). □

Clearly, whether the estimates of the lemma hold for p=1 or p=2 depends on which ratio is larger in (4.14); or equivalently, which ratio is larger between ∥u∥1/∥u∥2 and ∥w∥1/∥w∥2. If u is from a random, (n−m)-dimensional subspace of \(\mathbb{R}^{n}\), then w is from its orthogonal complement—a random, m-dimensional subspace. When n−m≫m, the KGG result indicates that it is more likely that ∥u∥1/∥u∥2<∥w∥1/∥w∥2; or equivalently, ∥w∥2/∥u∥2<∥w∥1/∥u∥1. In this case, the lemma holds more likely for p=1 than for p=2.

Corollary 4.4

Let \(U\,{\in}\,\mathbb{R}^{n \times m}\) with m < n have orthonormal columns so that U T U = I. Let \(x,y \in\mathbb{R}^{n}\) satisfy ∥y∥1⩽∥x∥1 and ∥U T y−d∥2⩽γ for some \(d\in\mathbb{R}^{m}\). Define u≜(I−UU T)(y−x) and w≜UU T(y−x). In addition, let k=∥x∥0 satisfy (4.6) whenever u≠0. Then

$$ \|y-x\|_p \leqslant \gamma_p(C_\nu+1) \bigl(\|U^Tx-d\|_2+\gamma\bigr), \quad p = 1\ \textit{or}\ 2, $$
(4.15)

where \(\gamma_{1}=\sqrt{n}\) and γ 2=1.

Proof

Noting that y=x+u+w and U T u=0, we calculate

$$ \gamma\geqslant \big\|U^T(x+u+w)-d\big\|_2 = \big\|U^Tw - \bigl(d-U^Tx\bigr)\big\|_2 \geqslant \big\|U^Tw \big\|_2 -\big \|U^Tx-d\big\|_2, $$

which implies

$$ \|w\|_2 = \big\|U^Tw\big\|_2 \leqslant \gamma+ \big\|U^Tx-d\big\|_2. $$
(4.16)

Combining (4.16) with (4.12), we arrive at (4.15) for either p=1 or 2, where in the case of p=1 we use the inequality \(\|w\|_{1} \leqslant \sqrt{n}\|w\|_{2}\). □

Proof of Theorem 4.1

Since \(\bar{x}\in\mathcal{F}(\gamma)\) and \(x_{\gamma}^{*}\) minimizes the 1-norm in \(\mathcal{F}(\gamma)\), we have \(\|x_{\gamma}^{*}\|_{1}\leqslant \|\bar{x}\|_{1}\). The proof then follows from applying Corollary 4.4 to \(y=x_{\gamma}^{*}\) and \(x=\bar{x}\), and the fact that the weighted norm defined in (4.1) satisfies ∥Ax−b∥ M =∥U T x−R −T b∥2. □

Proof of Theorem 4.2

We note that condition (4.8) is equivalent to \(\|x_{0}^{*}\|_{1}\leqslant \|\hat{x}(k)\|_{1}\) since \(\|\hat{x}\|_{1}=\|\hat {x}-\hat{x}(k)\|_{1} +\|\hat{x}(k)\|_{1}\). Upon applying Lemma 4.3 to \(y=x_{0}^{*}\) and \(x=\hat{x}(k)\) with u=P n (y−x) and w=P r (y−x), and also noting \(P_{r}x_{0}^{*}=P_{r}\hat{x}\), we have

$$\big\|x_0^*-\hat{x}(k)\big\|_p \leqslant (C_\nu+1) \big\|P_r\bigl(\hat{x}(k)-\hat{x}\bigr)\big\|_p, $$

which completes the proof. □

5 Uniform Recoverability

The recoverability result, Theorem 3.2, is derived essentially only for standard normal random matrices. It has been empirically observed (see [15, 16], for example) that recovery behavior of many different random matrices seems to be identical. We call this phenomenon uniform recoverability. In this section, we provide a theoretical explanation to this property.

5.1 Preliminaries

We will consider the simple case where \(\varOmega=\mathbb{R}^{n}\) and γ=0 so that we can make use of the necessary and sufficient condition in Proposition 2.3. We first translate this necessary and sufficient condition into a form more conducive to our analysis.

For 0<k<n, we define the following function that maps a vector in \(\mathbb{R}^{n}\) to a scalar:

$$ \lambda_k(v) \triangleq \frac{\|v\|_1-2\|v(k)\|_1}{\|v\|_2},\quad v \ne0, $$
(5.1)

where v(k) is a k-term approximation of v whose nonzero elements are the k largest elements of v in magnitude. It is important to note that λ k (v) is invariant with respect to multiplications by scalars (or scale-invariant) and permutations of v. Moreover, λ k (v) is continuous, and achieves its minimum and maximum (since its domain can be restricted to the unit sphere).

Proposition 5.1

Given \(A\in\mathbb{R}^{m \times n}\) with m<n, the equivalence (2.12), i.e.,

$$\{\bar{x}\} = \mathop{\operatorname{arg}\min}\bigl\{\|x\|_1: Ax=A\bar {x}\bigr\}, $$

holds for all \(\bar{x}\) with \(\|\bar{x}\|_{0} \leqslant k\) if and only if

$$ 0 < \varLambda_k(A) \triangleq \min\bigl\{\lambda_k(v): v \in\mathcal{N}(A)\setminus\{0\}\bigr\}. $$
(5.2)

Proof

For any fixed v≠0, the condition ∥v∥1>2∥v α ∥1 in (2.13) for all index sets α with |α|⩽k is clearly equivalent to λ k (v)>0. After taking the minimum over all v≠0 in \(\mathcal{N}(A)\), we see that Λ k (A)>0 is equivalent to the necessary and sufficient condition in Proposition 2.3. □

For notational convenience, given any \(A \in\mathbb{R}^{m \times n}\) with m<n, let us define the set

$$ \mathbf{sub}(A) = \bigl\{B \in\mathbb{R}^{m \times(m+1)}: \mbox{$B$ is a submatrix of $A$} \bigr\}. $$

In other words, each member of sub(A) is formed by m+1 columns of A in their original order. Clearly, the cardinality of sub(A) is n choose m+1. We say that the set sub(A) has full rank if every member of sub(A) has rank m. It is well known that for most distributions, sub(A) will have full rank with high probability.

5.2 Results for Uniform Recoverability

When \(A\in\mathbb{R}^{m \times n}\) is randomly chosen from a probability space, Λ k (A) is a random variable whose sign, according to Proposition 5.1, determines the success or failure of recovery for all \(\bar{x}\) with \(\|\bar{x}\|_{0}\leqslant k\). In this setting, the following theorem indicates that Λ k (A) is a sample minimum of another random variable λ k (d(B)) where \(B \in\mathbb{R}^{m \times (m+1)}\) is from the same probability distribution as A, and \(d(B) \in \mathbb{R}^{m+1}\) is defined by

$$ \bigl[d(B)\bigr]_i \triangleq\big|\det(B_i)\big|, \quad i =1,\cdots,m+1, $$
(5.3)

where \(B_{i} \in\mathbb{R}^{m \times m}\) is the submatrix of B obtained by deleting the i-th column of B.

Theorem 5.2

Let \(A \in\mathbb{R}^{m\times n}\) (m<n) with sub(A) of full rank (i.e., every member of sub(A) has rank m). Then for k⩽m

$$ \varLambda_k(A) = \min \bigl\{\lambda_k \bigl(d(B)\bigr): B \in\mathbf{sub}(A) \bigr\}, $$
(5.4)

where \(d(B) \in\mathbb{R}^{m+1}\) is defined in (5.3).

The proof of this theorem is left to Sect. 5.4.

Remark 5

Theorem 5.2, together with Proposition 5.1, establishes that recoverability is determined by the properties of d(B), not directly those of A. If distributions of d(B) for different types of random matrices converge to the same limit as m→∞, then asymptotically there should be an identical recovery behavior for different types of random matrices.

For any random matrix B, by definition the components of d(B) are random determinants (in absolute value). It has been established by Girko [18] that a wide class of random determinants (in absolute value) does share a limit distribution (see the book by Girko [19] for earlier results).

Theorem 5.3

(Girko)

For any m, let the random elements \(t_{ij}^{(m)}\), 1⩽i,j⩽m, of the matrix \(T_{m}=[t_{ij}^{(m)}]\) be independent,

$$\mathbf{E}(t_{ij}^{(m)})=\mu ,\quad \mathbf{Var}(t_{ij}^{(m)})=1\quad \textit{and} \quad\sup_{i,j,m}\mathbf{E}|t_{ij}^{(m)}|^{4+\delta} < \infty$$

for some δ>0. Then

$$ \lim_{m\rightarrow\infty}\mathbf{Prob} \biggl\{ \frac{\log (\det(T_m)^2/[(m-1)!(1+m\mu^2)] )}{ \sqrt{2\log{m}}} < t \biggr\} = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^te^{-\frac{x^2}{2}}dx. $$
(5.5)

Theorem 5.3 says that for a wide class of random determinants squared, their logarithms, with proper scalings, converge in distribution to the standard normal law; or the limit distribution of the random determinants squared is log-normal.

Remark 6

Since the elements of d(B) are random determinants in absolute value, they all have the same limit distribution as long as B satisfies the conditions of Theorem 5.3.

The elements of d(B) are not independent in limit, because any two of them are determinants of m×m matrices that share m−1 common columns. However, the cause of such dependency among elements of d(B) is purely algebraic, and hence does not vary with the type of random matrices. To stress this point, we mention that for a wide range of random matrices B, the ratios det(B i )/det(B j ), i≠j, converge to Cauchy distribution with the cumulative distribution function 1/2+arctan(t)/π. This result can be found, in a slightly different form, in Theorem 15.1.1 of the book by Girko [19].

Remark 7

We observe from (5.5) that the mean values μ only affect the scaling factor of the determinant, but not the asymptotic recoverability behavior since λ k (⋅) is scale-invariant, implying that measurement matrices need not have zero mean, as is usually required in earlier theoretical results of this sort. In addition, the unit variance assumption in Theorem 5.3 is not restrictive because it can always be achieved by scaling.

5.3 Numerical Illustration

To illustrate the uniformity of CS recovery, we sample the random variable λ k (d(B)) for \(B\in\mathbb{R}^{m\times(m+1)}\) whose entries are i.i.d. and randomly drawn from one of the two probability distributions: the standard normal distribution \(\mathcal{N}(0,1)\) or the uniform distribution on the interval [0,1]. While the former has zero mean, the latter has mean 1/2. In Fig. 4, we plot the empirical density functions (namely, scaled histograms) of λ k (d(B)) for the two random distributions with different values of m, k and sample size. Recall that successful recovery of all k-sparse signals is guaranteed for matrix A if and only if the sample minimum of λ k (d(B)) over sub(A) is positive.

Fig. 4
figure 4

Empirical density functions of λ k (d(B)) for 2 random distributions

Full size image

As can be seen from Fig. 4, even at m=50, the two empirical density functions for λ 10(d(B)), corresponding to the standard normal (solid line) and the uniform distributions (small circles) respectively, are already fairly close. At m=200, the two empirical density functions for λ 40(d(B)) become largely indistinguishable in most places.

5.4 Proof of Theorem 5.2

The following result, established by Eydelzon [16] in a slightly different form, will play a key role in the proof. For completeness, we include a proof for it.

Lemma 5.4

Let \(\mathcal{V}\) be an (n−m)-dimensional subspace of \(\mathbb {R}^{n}\) and k⩽m<n. If \(\hat{v} \in\mathcal{V}\) minimizes λ k (v) in \(\mathcal{V}\), then \(\hat{v}\) has at least n−m−1 zeros, or equivalently at most m+1 nonzeros.

Proof

Let \(\mathcal{V}\) be spanned by the orthonormal columns of \(Q \in \mathbb{R}^{n \times (n-m)}\) (so Q T Q=I) and \(\hat{v}=Q\hat{s}\) minimizes λ k (v) in \(\mathcal{V}\) for some \(\hat{s}\in\mathbb{R}^{n-m}\). Assume, without loss of generality, that \(\|\hat{v}\|_{2}=\|Q\hat{s}\|_{2}=\|\hat{s}\|_{2}=1\). We now prove the result by contradiction.

Suppose that \(\hat{v}\) has at most n−m−2 zeros, say, \(\hat{v}_{i}=q_{i}^{T}\hat{s}=0\) for i=1,2,⋯,n−m−2 where \(q_{i}^{T}\) is the i-th row of Q. Then there must exist a unit (in the 2-norm) vector \(h \in\mathbb{R}^{n-m}\) that is perpendicular to \(\hat{s}\) and q i for i=1,2,⋯,n−m−2. By construction,

$$(\hat{v}+\tau Qh)_i=0, \quad i=1,2,\cdots,n-m-2, $$

for any scalar value τ. By setting τ sufficiently small in absolute value, say |τ|⩽ϵ, we can ensure for i>n−m−2 that \(\operatorname{sign}((\hat{v}+\tau Qh)_{i})=\operatorname{sign}(\hat{v}_{i})\) so that

$$\big|(\hat{v}+\tau Qh)_i\big|=\operatorname{sign}(\hat{v}_i) (\hat{v}+ \tau Qh)_i =|\hat{v}_i|+\tau \operatorname{sign}( \hat{v}_i) (Qh)_i, \quad \forall i > n-m-2. $$

Now we evaluate λ k (⋅) at \(v = \hat{v} + \tau Qh\) for 0<|τ|⩽ϵ (with a yet undecided sign for τ),

(5.6)

where \(\sqrt{1+\tau^{2}}=\|v\|_{2}=\|\hat{s}+\tau h\|_{2}\) and for some index set J with |J|=k,

$$ \omega= \sum_{i=n-m-1}^n\operatorname{sign}( \hat{v}_i) (Qh)_i -2\sum_{i \in J} \operatorname{sign}(\hat{v}_i) (Qh)_i. $$

If ω≠0, we set \(\operatorname{sign}(\tau)=-\operatorname{sign}(\omega)\) so that τω<0. Now a contradiction, \(\lambda_{k}(v)<\lambda_{k}(\hat{v})\), arises from (5.6). So \(\hat{v}\) must have at least n−m−1 zeros or at most m+1 nonzeros. □

Proof of Theorem 5.2

In view of Lemma 5.4 with \(\mathcal{V}=\mathcal{N}(A)\), to find Λ k (A) it suffices to evaluate the minimum of λ k (⋅) over all those vectors in \(\mathcal {N}(A)\setminus\{0\}\) that have at most m+1 nonzeros.

Without loss of generality, let \(v\in\mathcal{N}(A)\setminus\{0\}\) so that v i =0 for all i>m+1, and let B=[b 1   b 2  ⋯  b m+1]∈sub(A) consist of the first m+1 columns of A. Then Av=Bu=0, where u consists of the first m+1 elements of v. Hence, \(u\in\mathbb{R}^{m+1}\) spans the null space of B which is one-dimensional (recall that sub(A) has full rank).

Let B i be the submatrix of B with its i-th column removed. Without loss of generality, we assume that det(B 1)≠0. Clearly, the null space of B is spanned by the vector

$$u=\left ( \begin{array}{c}-1 \\[3pt] B_1^{-1}b_1 \end{array} \right ) \in\mathbb{R}^{m+1}, $$

where, by Crammer’s rule, \((B_{1}^{-1}b_{1})_{i}=\det(B_{i+1})/\det(B_{1})\), i=1,2,⋯,m. Since the function λ k (⋅) is scale-invariant, to evaluate λ k (⋅) at \(v\in\mathcal{N}(A)\setminus\{0\}\) with v i =0 for i>m+1, it suffices to evaluate it at d(B)≜|det(B 1)u|, which coincides with the definition in (5.3).

Obviously, the exactly same argument can be equally applied to all other nonzero vectors in \(\mathcal{N}(A)\) which have at most m+1 nonzeros in different locations, corresponding to different members of sub(A). This completes the proof. □

6 Conclusions

CS is an emerging methodology with a solid theoretical foundation that is still evolving. Most previous analyses in the CS theory relied on the RIP of the measurement matrix A. These analyses can be called matrix-based. The non-RIP analysis presented in this paper, however, is subspace-based, and utilizes the classic KGG inequality to supply the order of recoverable sparsity. It should be clear from this non-RIP analysis that CS recoverability and stability, when using the equation Ax=b, are solely determined by the properties of the subspaces associated with A regardless of matrix representations.

The non-RIP approach used in this paper has enabled us to derive the extended recoverability and stability results immediately from a couple of remarkably simple observations (Lemmas 2.1 and 4.3) on the 2-norm versus 1-norm ratio in the null space of A. The obtained extensions include: (a) allowing the use of prior information in recovery, (b) establishing RIP-free formulas for stability constants, and (c) explaining the uniform recoverability phenomenon. In our view, these new results reinforce the theoretical advantages of ℓ 1-minimization-based CS decoding models.

As has been alluded to at the beginning, there are topics in the CS theory that are not covered in this work, one of which is that the recoverable sparsity order given in Theorem 3.2 can be shown to be optimal in a sense (see [4] for an argument). Nevertheless, it is hoped that this work will help enhance and enrich the theory of CS, make the theory more accessible, and stimulate more activities in utilizing prior information and different measurement matrices in CS research and practice.