Skip to main content
SpringerLink
Log in

A Fuzzy Time Series Model Based on Improved Fuzzy Function and Cluster Analysis Problem

  • Published:
Communications in Mathematics and Statistics Aims and scope Submit manuscript

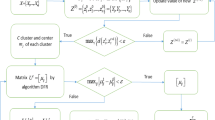
Abstract

Based on the improvement in establishing the relations of data, this study proposes a new fuzzy time series model. In this model, the suitable number of fuzzy sets and their specific elements are determined automatically. In addition, using the percentage variations of series between consecutive periods of time, we build the fuzzy function. Incorporating all these improvements, we have a new fuzzy time series model that is better than many existing ones through the well-known data sets. The calculation of the proposed model can be performed conveniently and efficiently by a MATLAB procedure . The proposed model is also used in forecasting for an urgent problem in Vietnam. This application also shows the advantages of the proposed model and illustrates its effectiveness in practical application.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Abbasov, A. M., Mamedova, M. H.: Application of fuzzy time series to population forecasting. In: CORP, Vienna University of Technology, pp. 545–552(2003)

  2. Aladag, C.H., Basaran, M.A., Egrioglu, E., Yolcu, U., Uslu, V.R.: Forecasting in high order fuzzy time series by using neural networks to define fuzzy relations. Expert Syst. Appl. 36, 4228–4231 (2013)

    Article  Google Scholar 

  3. Aladag, C.H., Yolcu, U., Egrioglu, E., Dalar, A.Z.: A new time invariant fuzzy time series forecasting method based on particle swarm optimization. Appl. Soft Comput. 12, 3291–3299 (2012a)

    Article  Google Scholar 

  4. Chen, S.M.: Forecasting enrollments based on fuzzy time series. Fuzzy Sets Syst. 81, 311–319 (1996)

    Article  Google Scholar 

  5. Chen, S.M., Hsu, C.: A new method to forecast enrollments using fuzzy time series. Int. J. Appl. Sci. Eng. 2, 3234–3244 (2004)

    Google Scholar 

  6. Chen, S.M., Kao, P.Y.: TAIEX forecasting based on fuzzy time series, particle swarm optimization techniques and support vector machines. Inf. Sci. 247, 62–71 (2013)

    Article  MathSciNet  Google Scholar 

  7. Chen, J.H., Hung, W.L.: An automatic clustering algorithm for probability density functions. J. Stat. Comput. Simul. 85, 3047–3063 (2015)

    Article  MathSciNet  Google Scholar 

  8. Cheng, C., Chen, T., Teoh, C.: Fuzzy time-series based on adaptive expectation model for Taifex forecasting. Expert Syst. Appl. 34, 1126–1132 (2008)

    Article  Google Scholar 

  9. Dincer, N.G., Akkus, O.: A new fuzzy time series model based on robust clustering for forecasting of air pollution. Ecol. Inf. (2017). https://doi.org/10.1016/j.ecoinf.2017.12.001

    Article  Google Scholar 

  10. Egrioglu, E., Aladag, C., Yolcu, U., Uslu, U., Basaran, M.A.: A new approach based on artificial neural networks for high order multivariate fuzzy time series. Expert Syst. Appl. 36, 10589–10594 (2009b)

    Article  Google Scholar 

  11. Egrioglu, E., Uslu, V., Yolcu, U., Basaran, M., Aladag, C.: A new approach based on artificial neural networks for high order bivariate fuzzy time series. Appl. Soft Comput. 58, 265–273 (2009c)

    Article  Google Scholar 

  12. Egrioglu, S., Bas, E., Aladag, C.H., Yolcu, U.: Probabilistic fuzzy time series method based on artificial neural network. Am. J. Intell. Syst. 62, 42–47 (2016)

    Google Scholar 

  13. Eren, B., Vedide, R., Uslu, U., Erol, E.: A modified genetic algorithm for forecasting fuzzy time series. Appl. Intell. 41, 453–463 (2014)

    Article  Google Scholar 

  14. Ghosh, H., Chowdhury, S.: An improved fuzzy time-series method of forecasting based on L-R fuzzy sets and its application. J. Appl. Stat. 43, 1128–1139 (2016)

    Article  MathSciNet  Google Scholar 

  15. Hao, T.: An improved fuzzy time series forecasting method using trapezoidal fuzzy numbers. Fuzzy Optim. Decis. Mak. 6, 63–80 (2016)

    MathSciNet  MATH  Google Scholar 

  16. Huarng, K.: Heuristic models of fuzzy time-series for forecasting. Fuzzy Sets Syst. 123, 369–386 (2001a)

    Article  MathSciNet  Google Scholar 

  17. Huarng, K.: Effective lengths of intervals to improve forecasting in fuzzy time series. Fuzzy Sets Syst. 12, 387–394 (2001b)

    Article  MathSciNet  Google Scholar 

  18. Huarng, K., Yu, T.: Ratio-based lengths of intervals to improve fuzzy time series forecasting. IEEE Trans. Syst. Man Cybern. Part B Cybern. 36, 328–340 (2001b)

    Article  Google Scholar 

  19. Khashei, M., Bijari, M., Hejazi, C.S.R.: An extended fuzzy artificial neural networks model for time series forecasting. Iran. J. Fuzzy Syst. 3, 45–66 (2011)

    MathSciNet  MATH  Google Scholar 

  20. Lee, H., Chou, M.: Fuzzy forecasting based on fuzzy time series. Int. J. Comput. Math. 81, 781–789 (2004)

    Article  MathSciNet  Google Scholar 

  21. Qiang, S., Brad, C.: Forecasting enrollments with fuzzy time series—Part II. Fuzzy Sets Syst. 62, 1–8 (1994)

    Article  Google Scholar 

  22. Richard, J.H., James, C.B.: Recent convergence results for the fuzzy c-means clustering algorithms. J. Classif. 5, 237–247 (1998)

    MathSciNet  Google Scholar 

  23. Singh, S.: A simple method of forecasting based on fuzzy time-series. Appl. Math. Comput. 186, 330–339 (1998)

    MathSciNet  MATH  Google Scholar 

  24. Singh, S.: A computational method of forecasting based on high-order fuzzy time series. Expert Syst. Appl. 36, 10551–10559 (2009)

    Article  Google Scholar 

  25. Song, Q., Chissom, B.: Fuzzy time series and its models. Fuzzy Sets Syst. 54, 269–277 (1993a)

    Article  MathSciNet  Google Scholar 

  26. Song, Q., Chissom, B.: Forecasting enrollments with fuzzy time series—part I. Fuzzy Sets Syst. 54, 1–9 (1993b)

    Article  Google Scholar 

  27. Song, Q., Chissom, B.: Forecasting enrollments with fuzzy time series—part II. Fuzzy Sets Syst. 62, 1–8 (1994)

    Article  Google Scholar 

  28. Sullivan, J., Woodall, W.: A comparison of fuzzy forecasting and markov modeling. Fuzzy Sets Syst. 64, 279–293 (1994)

    Article  Google Scholar 

  29. Teoh, H., Cheng, C., Chu, H., Chen, J.: Fuzzy time series model based on probabilistic approach and rough set rule induction for empirical research in stock markets. Data Knowl. Eng. 67, 103–117 (2008)

    Article  Google Scholar 

  30. Tai, V.V.: An improved fuzzy time series forecasting model using variations of data. Fuzzy Optim. Decis. Mak. 18, 151–173 (2019)

    Article  MathSciNet  Google Scholar 

  31. Tai, V.V., Nghiep, L.D.: A New fuzzy time series model based on cluster analysis problem. Int. J. Fuzzy Syst. 21, 852–864 (2019)

    Article  Google Scholar 

  32. Zhiqiang, Z., Qiong, Z.: Fuzzy time series forecasting based on k-means clustering. Open J. Appl. Sci. 25, 100–103 (2012)

    Google Scholar 

  33. Yu, H.K.: Weighted fuzzy time-series models for TAIEX forecasting. Phys. A 349, 609–624 (2005)

    Article  Google Scholar 

  34. Yu, H.K., Huarng, K.: A neural network- based fuzzy time series model to improve forecasting. Expert Syst. Appl. 37, 3366–3372 (2010)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Science, Can Tho University, Can Tho, Vietnam

    Tai Vovan

  2. Vinh Long University Technology and Education, Vinh Long, Vietnam

    Thuy Lethithu

Authors
  1. Tai Vovan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thuy Lethithu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tai Vovan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vovan, T., Lethithu, T. A Fuzzy Time Series Model Based on Improved Fuzzy Function and Cluster Analysis Problem. Commun. Math. Stat. 10, 51–66 (2022). https://doi.org/10.1007/s40304-019-00203-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40304-019-00203-5

Keywords

Mathematics Subject Classification

Search

Navigation