Skip to main content
SpringerLink
Log in

On Nonlinear Dynamic Modeling for a Rotating Paraboloidal Thin-Shell Appendage Attached to a Spacecraft Mechanism with Paraboloidal Curved Shell Element

  • Published:
The Journal of the Astronautical Sciences Aims and scope Submit manuscript

Abstract

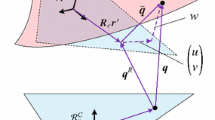
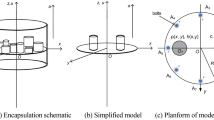
A methodology for modeling a rotating paraboloidal thin-shell structure attached to a spacecraft body is proposed considering its geometric nonlinear effect. Instead of using conventional shell elements to discretize the paraboloidal thin-shell in the Cartesian coordinate, the paraboloidal coordinates in the meridional, circumferential and normal directions are employed to completely express the deformations of the curved thin-shell. Then, explicit expressions for the generalized elastic forces and stiffness varying matrices are deduced on the basis of exact strain-displacement relations. And, the rigid-flexible coupled dynamic model for the flexible multibody system is derived by the principle of virtual work. In contrast with the previous modeling approaches, the present method shows an advantage in avoiding large calculation quantity of nonlinear stiffness matrix due to more formalized. Furthermore, a full analysis with specific numerical simulation is achieved by using the present model and conventional shell model, respectively. All simulation results obtained by the two modeling methods verify the correctness and better convergence of the proposed methodology.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Silverberg, L.M., Park, S.: Interactions between rigid-body and flexible-body motions in maneuvering spacecraft. J. Guid. Control. Dyn. 13(1), 73–81 (1990)

    Article  MathSciNet  Google Scholar 

  2. Ryan, R.: Simulation of actively controlled spacecraft with flexible appendages. J. Guid. Control. Dyn. 13(4), 691–702 (1990)

    Article  Google Scholar 

  3. Utku, S., Shoemaker, W.L., Salama, M.: Nonlinear equations of dynamics for spinning paraboloidal antennas. Comput. Struct. 16(1), 361–370 (1983)

    Article  Google Scholar 

  4. Shoemaker, W.L.: The nonlinear dynamics of spinning paraboloidal antennas. PhD. Dissertation, Duke University, Durham, North Carolina (1983)

  5. Shoemaker, W.L., Utku, S.: On the free vibrations of spinning paraboloids. J. Sound Vib. 111(2), 279–296 (1986)

    Article  Google Scholar 

  6. Leissa, A.W., Kang, J.H.: Three-dimensional vibration analysis of paraboloidal shells. JSME Int. J. 45(1), 2–7 (2002)

    Article  Google Scholar 

  7. Kang, J.H., Leissa, A.W.: Free vibration analysis of complete paraboloidal shells of revolution with variable thickness and solid paraboloids from a three-dimensional theory. Comput. Struct. 83(31–32), 2594–2608 (2005)

    Article  Google Scholar 

  8. Al-Khatib, O.J.: Vibration of Paraboloidal Shells. PhD. Dissertation, Tennessee Technological University (2006)

  9. Al-Khatib, O.J., Buchanan, G.R.: Free vibration of a paraboloidal shell of revolution including shear deformation and rotary inertia. Thin-Walled Struct. 48(3), 223–232 (2010)

    Article  Google Scholar 

  10. Boutaghou, Z.E., Erdman, A.G., Stolarski, H.K.: Dynamics of flexible beams and plates in large overall motions. Asme. T. 59(4), 991–999 (1991)

    Article  Google Scholar 

  11. Yoo, H.H., Chung, J.: Dynamics of rectangular plates undergoing prescribed overall motion. J. Sound Vib. 239(1), 123–137 (2001)

    Article  Google Scholar 

  12. Liu, J.Y., Hong, J.Z.: Dynamic modeling and modal truncation approach for a high-speed rotating elastic beam. Arch. Appl. Mech. 72(8), 554–563 (2002)

    Article  Google Scholar 

  13. Park, J.H., Kim, J.H.: Dynamic analysis of rotating curved beam with a tip mass. J. Sound Vib. 228(5), 1017–1034 (1999)

    Article  Google Scholar 

  14. Sugiyama, H., Koyama, H., Yamashita, H.: Gradient deficient curved beam element using the absolute nodal coordinate formulation. J. Comput. Nonlinear Dyn. 5(2), 1090–1097 (2010)

    Google Scholar 

  15. Pan, K.Q., Liu, J.Y.: Geometric nonlinear dynamic analysis of curved beams using curved beam element. Acta. Mech. Sin. 27(6), 1023–1033 (2011)

    Article  MathSciNet  Google Scholar 

  16. Bauchau, O.A., Choi, J.Y., Bottasso, C.L.: On the modeling of shells in multibody dynamics. Multibody. Syst. Dyn. 8(4), 459–489 (2002)

    Article  Google Scholar 

  17. Lubowiecka, I., Chróścielewski, J.: On dynamics of flexible branched shell structures undergoing large overall motion using finite elements. Comput. Struct. 80(9), 891–898 (2002)

    Article  Google Scholar 

  18. Betsch, P., Sänger, N.: On the use of geometrically exact shells in a conserving framework for flexible multibody dynamics. Comput. Method. Appl. Mech. Eng. 198(17–20), 1609–1630 (2009)

    Article  MathSciNet  Google Scholar 

  19. Goyal, A., Dörfel, M.R., Simeon, B., Vuong, A.V.: Isogeometric shell discretizations for flexible multibody dynamics. Multibody. Syst. Dyn. 30(2), 139–151 (2013)

    Article  MathSciNet  Google Scholar 

  20. Tzou, H.S., Ding, J.H.: Optimal control of precision paraboloidal shell structronic systems. J. Sound Vib. 276(1), 273–291 (2002)

    MathSciNet  MATH  Google Scholar 

  21. You, B.D.: Analysis and control of dynamic pointing accuracy for satellite antenna. PhD. Dissertation, School of Astronautics, Harbin Institute of Technology (2011)

Download references

Acknowledgments

This material is partially based upon Project (No. 51575126) supported by the National Natural Science Foundation of China, and projects (Nos. 2013 M541358 and 2015 T80358) funded by China Postdoctoral Science Foundation, and Project (No. WH20150108) supported by Discipline Construction Guide Foundation in Harbin Institute of Technology at Weihai.

Author information

Authors and Affiliations

  1. School of Naval Architecture and Ocean Engineering, Harbin Institute of Technology, Weihai, China

    Bindi You, Yiming Sun, Peibo Hao, Dong Liang & Zhihui Gao

Authors
  1. Bindi You
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yiming Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Peibo Hao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Dong Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Zhihui Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bindi You.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

You, B., Sun, Y., Hao, P. et al. On Nonlinear Dynamic Modeling for a Rotating Paraboloidal Thin-Shell Appendage Attached to a Spacecraft Mechanism with Paraboloidal Curved Shell Element. J Astronaut Sci 66, 383–403 (2019). https://doi.org/10.1007/s40295-018-00142-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40295-018-00142-3

Keywords

Search

Navigation