Skip to main content
SpringerLink
Log in

A Radial Axial-symmetric Intermediary Model for the Roto-orbital Motion

  • Published:
The Journal of the Astronautical Sciences Aims and scope Submit manuscript

Abstract

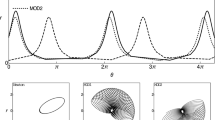
We study the roto-orbital dynamics of a uniform sphere and a body with axial symmetry by means of a radial intermediary, which defines an integrable system. Numerical comparisons of the MacCullagh’s truncation of the gravity gradient potential and intermediary models are performed, concluding that the intermediary provides a valuable approximation with small differences when compared with the MacCullagh’s one. Our analysis includes the analytical integration and a study of the special solutions and relative equilibria.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Abbreviations

A, B, C,:

Principal moments of inertia

A :

Rotation matrix relating vectors in the body \(\mathcal {B}_{1}\) and inertial frames

b i :

Body frame vectors

\(\mathcal {B}_{1}\) :

Body with mass m 1

\(\mathcal {B}_{2}\) :

Body with mass m 2. Main body

e :

Eccentricity

E i :

Spatial frame vectors

\(\mathcal {G}\) :

Universal gravitational constant

G, G o , G r :

Total, orbital, rotational angular momentum vectors in body frame

G, G o , G r :

Modulus of the corresponding vectors

\(\mathcal H\) :

Hamilton function of the intermediary model

\(\mathcal {H}_{K}\) :

Kepler system

\(\mathcal {H}_{E}\) :

Free rigid body

\(\mathcal {H}_{0}\) :

Zero order Hamiltonian (\(\mathcal {H}_{0}=\mathcal {H}_{K}+\mathcal {H}_{E}\))

I :

Moment of inertia tensor relative to the body \(\mathcal {B}_{1}\)

I o :

Angle between π o and π

I r :

Angle between π r and π

I :

Inclination of the total angular momentum plane

I Δ :

Inclination of the rotational plane

I Θ :

Inclination of the orbital plane

ℓ :

Node of the total angular momentum plane

ℓ I :

Body plane (see π b ) and rotational planes intersection

ℓ r ,−ℓ o :

Total, orbital and rotational planes intersection

ℓ μ δ :

Rotational and spatial planes intersection

M :

Total mass of the system

m :

Reduced mass of the system

m i :

Mass of the body \(\mathcal {B}_{i}\)

n :

Unitary vector parallel to the total angular momentum

N, N ′ :

Third component of G r

\(\mathcal {P}\) :

Perturbation

p :

Linear momentum associated to r

q :

m/m 1

r, r ′ :

Modulus of the vector joining the mass center of the bodies

r :

Vector joining the mass center of the bodies

R, R ′ :

Radial velocity of the center of mass

R 1 :

Distance between the center of mass and the furthest point of \(\mathcal {B}_{1}\)

R 2 :

Distance between the center of mass and the furthest point of \(\mathcal {B}_{2}\)

R i :

Position vector of the body \(\mathcal {B}_{i}\) in the inertial frame

U :

MacCullagh’s term

\(\mathcal {V}\) :

Potential of the intermediary model

γ i :

Direction cosines of r/r

δ, δ ′ :

Argument of the angle between ℓ r and ℓ I

Δ, Δ′ :

Magnitude of the angular momentum of the rigid body

𝜃, 𝜃 ′ :

Argument of the vector joining the center of masses of the two bodies

Θ, Θ′ :

Magnitude of the angular momentum of the center of mass

ι :

I o + I r

κ :

\(\mathcal {G}M\)

λ :

Argument of the node relative to the Andoyer plane

μ,:

Argument of the angle between ℓ μ δ and ℓ I

ν, ν ′ :

Argument of the angle between ℓ I and b 1

# #π# # :

Angular momentum of the body B 1

π:

Total angular momentum plane

π b :

Body plane, b 1 b 2-plane

π o :

Orbital plane

π r :

Andoyer plane

ρ m i n :

R 1 + R 2

σ :

Angle between π r and the body plane

ϕ, ϕ ′ :

Argument of the node of the total angular momentum plane

Φ, Φ′ :

Third component of the total angular momentum in space frame

ψ, ψ ′ :

Argument of ℓ r

Ψ, Ψ′ :

Magnitude of the total angular momentum

Ω i :

Angular velocity in the body frame

References

  1. Abolenaga, M., Barkin, Y.: Stationary motion of a rigid body in the attraction field of a sphere. Astronom. Zh. 56(3), 881–886 (1979)

    MATH  Google Scholar 

  2. Byrd, P.F., Friedman, M.D.: Handbook of Elliptic Integrals for Engineers and Scientists. Springer, Berlin (1971)

    Book  MATH  Google Scholar 

  3. Cardoso, J., Ferrer, S., Scheeres, D.J.: Intermediaries in Gravity-gradient Roto-orbital Dynamics. In preparation (2017)

  4. Chernousko, F.L.: On the motion of a satellite about its center of mass under the action of gravitational moments. J. Appl. Math. Mech. 27(3), 708–722 (1963)

    Article  MathSciNet  Google Scholar 

  5. Cid, R., Ferrer, S., Elipe, A.: Regularization and linearization of the equations of motion in central force-fields. Celest. Mech. 31, 73–80 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  6. Crespo, F.: Hopf Fibration Reduction of a Quartic Model. An Application to Rotational and Orbital Dynamics. PhD Thesis, Universidad de Murcia (2015)

    Google Scholar 

  7. Deprit, A.: The elimination of the parallax in satellite theory. Celest. Mech. 24(2), 111–153 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  8. Deprit, A.: Elimination of the nodes in problem of. N bodies. Celestial Mech. 30(2), 181–195 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  9. Duboshin, G.: On one particular case of the problem of the translational-rotational motion of two bodies. Sov. Astron. 3, 154 (1959)

    Google Scholar 

  10. Ferrándiz, J.M.: Linearization in special cases of perturbed Keplerian motions. Celest. Mech. 39, 23–31 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  11. Ferrándiz, J.M., Ferrer, S., Sein-Echaluce, M.L.: Generalized elliptic anomalies. Celest. Mech. 40, 315–328 (1987)

    Article  MATH  Google Scholar 

  12. Ferrándiz, J.M., Sansaturio, M.E.: Elimination of the nodes when the satellite is a non spherical rigid body. Celest. Mech. 46, 307–320 (1989)

    Article  MATH  Google Scholar 

  13. Ferrer, S., Lara, M.: On roto-translatory motion: Reductions and radial intermediaries. J. Astronaut. Sci. 59, 21–39 (2012)

    Article  Google Scholar 

  14. Ferrer, S., Molero, F.J.: Intermediaries for gravity-gradient attitude dynamics I. Action-angle variables. Adv. Astronaut. Sci. 153, 293–312 (2014)

    Google Scholar 

  15. Gurfil, P., Lara, M.: Satellite onboard orbit propagation using Deprit’s radial intermediary. Celest. Mech. Dyn. Astron. 120, 217–232 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  16. Kinoshita, H.: Stationary motions of an axisymmetric body arround a spherical body and their stabilities. Publ. Astronom. Soc. Japan 22, 383–403 (1970)

    Google Scholar 

  17. Kinoshita, H.: Stationary motions of a triaxial body and their stabilities. Publ. Astronom. Soc. Japan 24, 409–417 (1972)

    Google Scholar 

  18. Lara, M., Gurfil, P.: Integrable approximation of j 2-perturbed relative orbits. Celest. Mech. Dyn. Astron. 114, 229–254 (2012)

    Article  MATH  Google Scholar 

  19. MacCullagh, J.: On the rotation of a solid body. Proc. R. Ir. Acad. 2, 520–545 (1840)

    Google Scholar 

  20. Muñoz Lecanda, M., Rodríguez-Olmos, M., Teixidó-Román, M.: Reduction of TSE(3) to the poisson structure for a symmetric top. J. Nonlinear Sci. 25(6), 1347–1390 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  21. Scheeres, D.: Relative equilbria for general gravity fields in the sphere-restricted full 2-body problem. Celest. Mech. Dyn. Astr. 94, 317–349 (2006)

    Article  MATH  Google Scholar 

  22. Scheeres, D.: Minimum energy configurations in the n-body problem and the celestial mechanics of granular systems. Celest. Mech. Dyn. Astr. 113, 291–320 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  23. Scheeres, D.: Orbital Motion in Strongly Perturbed Environments: Application to Asteroid Comet and Planetary Satellite Orbiters. Jointly published with Praxis Publishing, UK (2012)

    Book  Google Scholar 

  24. Vereshchagin, M., Maciejewski, A.J., Goździewski, K.: Relative equilibria in the unrestricted problem of a sphere and symmetric rigid body. Mon. Not. R. Astron. Soc. 403, 848–858 (2010)

    Article  Google Scholar 

  25. Wang, L., Krisshnaprasad, P., Maddocks, J.: Hamiltonian dynamics of a rigid body in central gravitational field. Celest. Mech. Dyn. Astron. 50, 349–386 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  26. Wang, L., Maddocks, J., Krisshnaprasad, P.: Steady rigid-body motions in a central gravitational field. J. Astronaut. Sci. 40, 449–478 (1992)

    MathSciNet  Google Scholar 

  27. Wolfram, S.: Mathematica 10.3.0.0, Student Edition. Wolfram Research Inc./Cambridge Univ. Press (2015)

Download references

Acknowledgments

Support from Research Agencies of Chile and Spain is acknowledged. They came in the form of the research projects 11160224, of the Chilean national agency FONDECYT and from the MTM2015-64095-P and ESP2013-41634-P, of the Ministry of Science of Spain. Partial support for one of the authors (S.F.) came from the Senior Mobility Program of the Ministry of Education of Spain. We deeply appreciate comments and suggestions of the referee which contributed to the improvement and clarity of the paper. We would also like to thank J. Cardoso for his efforts in collating numerical experiments.

Author information

Authors and Affiliations

  1. Facultad de Ciencias Departamento Matemática, Grupo GISDA, Universidad del Bío-Bío, Collao 1202, Casilla 5-C., Concepción, Chile

    F. Crespo

  2. Space Dynamic Group, DITEC, Facultad Informatica, Universidad de Murcia, Murcia, Spain

    F. J. Molero & S. Ferrer

  3. Department of Aerospace Engineering Sciences, University of Colorado at Boulder, Boulder, CO, 80309, USA

    D. J. Scheeres

Authors
  1. F. Crespo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. J. Molero
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Ferrer
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. D. J. Scheeres
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to F. Crespo.

Additional information

S. Ferrer was on a sabbatical leave at the Department of Aerospace Engineering Sciences, University of Colorado at Boulder.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Crespo, F., Molero, F.J., Ferrer, S. et al. A Radial Axial-symmetric Intermediary Model for the Roto-orbital Motion. J of Astronaut Sci 65, 1–28 (2018). https://doi.org/10.1007/s40295-017-0121-9

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40295-017-0121-9

Keywords

Search

Navigation