Skip to main content
SpringerLink
Log in

Nonlinear Observability for Relative Orbit Determination with Angles-Only Measurements

  • Published:
The Journal of the Astronautical Sciences Aims and scope Submit manuscript

Abstract

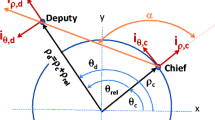
This paper presents nonlinear observability criteria for the relative orbital dynamics represented by the solutions of the two-body problem. It is assumed that a chief is on a circular orbit with a prescribed orbital radius, and it measures lines-of-sight toward a deputy only. A differential geometric method, based on the Lie derivatives, is used to derive sufficient conditions for observability of the orbital properties of the deputy. It is shown that under certain geometric conditions on the relative configuration between the chief and the deputy, the nonlinear relative motion is observable from angles-only measurements. The second part of this paper presents a quantitative measure of observability for the relative orbits, and it is formulated by generalizing the observability Gramian of linear dynamic systems. An extended Kalman filter is also developed to numerically illustrate the observability of nonlinear relative orbits with angles-only measurements and to show correspondence between the proposed observability measure and filtered solution accuracy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Brown, R.: Not just observable, but how observable. In: Proceedings of the National Electronic Conference, vol. 22, pp 709–714 (1966)

  2. Hahn, J., Edgar, T.: An improved method for nonlinear model reduction using balancing of empirical gramians. Comput. Chem. Eng. 26, 1379–1397 (2002)

    Article  Google Scholar 

  3. Hahn, J., Edgar, T., Marquardt, W.: Controllability and observability covariance matrices for the analysis and order reduction of stable nonlinear systems. J. Process Control 13, 115–127 (2003)

    Article  Google Scholar 

  4. Hermann, R., Krener, A.J.: Nonlinear controllability and observability. IEEE Trans. Autom. Control 22(5), 728–740 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  5. Krener, A., Ide, K.: Measures of unobservability. In: Proceedings of the IEEE Conference on Decision and Control, pp 6401–6406 (2009)

  6. Lall, S., Marsden, J., Glavaski, S.: Empirical model reduction of controlled nonlinear systems. In: Proceedings of the IFAC World Congress (1999)

  7. Lall, S., Marsden, J., Glavaski, S.: A subspace approach to balanced truncation for model reduction of nonlinear control systems. Int. J. Robust Nonlinear Control 12(6), 519–539 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  8. Lovell, T., Lee, T.: Nonlinear observability for relative satellite orbits with angles-only measurements. In: Proceedings of the International Symposium on Space Flight Dynamics (2014)

  9. Monzingo, R.: A note on sensitivity of system observability. IEEE Trans. Autom. Control 12(3), 314–315 (1967)

    Article  MathSciNet  Google Scholar 

  10. Müller, P., Weber, H.: Analysis and optimization of certain qualities of controllability and observability for linear dynamical systems. Automatica 8(3), 237–246 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  11. Newman, A., Krishnaprasad, P.: Computation for nonlinear balancing. In: Proceedings of the IEEE Conference on Decision and Control, pp. 4103–4104 (1998)

  12. Nijmeijer, H., van der Schaft, A.: Nonlinear Dynamical Control Systems. Springer (1990)

  13. Patel, H., Lovell, T.A., Allgeier, S., Russell, R., Sinclair, A.: Relative navigation for satellites in close proximity using angles-only observations. In: Proceedings of the AAS/AIAA Space Flight Mechanics Meeting (2012). AAS 12-202

  14. Scherpen, J.: Balancing for nonlinear systems. Syst. Control Lett. 21, 143–153 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  15. Scherpen, J.: Balancing for Nonlinear Systems. Ph.D. dissertation. University of Twente (1994)

  16. Woffinden, D., Geller, D.: Observability criteria for angles-only navigation. IEEE Trans. Aerosp. Electron. Syst. 45(3), 1194–1208 (2009)

    Article  Google Scholar 

  17. Yim, J., Crassidis, J., Junkins, J.: Autonomous orbit navigation of two spacecraft system using relative line of sight vector measurements. In: Proceedings of the AAS/AIAA Spaceflight Mechanics Meeting (2004). AAS 04-257

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical and Aerospace Engineering, The George Washington University, Washington, DC, 20052, USA

    Evan Kaufman & Taeyoung Lee

  2. Air Force Research Laboratory, Space Vehicles Directorate, Kirtland AFB, NM, USA

    T. Alan Lovell

Authors
  1. Evan Kaufman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Alan Lovell
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Taeyoung Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Evan Kaufman.

Additional information

This research has been supported in part by NSF under the grants CMMI-1243000 (transferred from 1029551), CMMI-1335008, and CNS-1337722.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kaufman, E., Lovell, T.A. & Lee, T. Nonlinear Observability for Relative Orbit Determination with Angles-Only Measurements. J of Astronaut Sci 63, 60–80 (2016). https://doi.org/10.1007/s40295-015-0082-9

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40295-015-0082-9

Keywords

Search

Navigation