Reducing Drug Wastage in Pharmaceuticals Dosed by Weight or Body Surface Areas by Optimising Vial Sizes

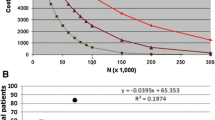
Abstract

Background

When pharmaceuticals are administered based on patient characteristics (for example weight or body surface area), an amount of product will be unused and must be disposed of. This wastage represents inefficiency and can distort decision making.

Methods

We present a method for the analysis of optimum fill volumes of pharmaceuticals to minimise wastage across a patient population, using publicly available data. Wastage for patients at each ‘step’ e.g. by kg of bodyweight is calculated, the frequency of each of these steps in the structure of the population is then estimated using the method of moments, with wastage then estimated for each ‘step’ multiplied by its prevalence. Illustrative examples of pembrolizumab and cabazitaxel show how wastage could be reduced using UK population data, whilst simultaneously reducing administrative burden.

Results

Changing the available vial sizes for pembrolizumab (available as 50 mg/100 mg vials) to 70 mg/100 mg, wastage could be cut from 13.3% to 8.7%. For cabazitaxel (only 60 mg vials available), increasing the fill to 70 mg could reduce wastage from 19.4% to 18.8%, or alternatively, adding a 12.5 mg vial reduce this to 6.5%. A secondary finding is that wastage is higher when the larger vial size is perfectly divisible by the smaller vial size.

Conclusions

Reductions in wastage have the potential to reduce the cost of manufacturing medicines, which is not necessarily low for novel products. These cost reductions could lead to increased profit (at the same prices), constant profit with a better return rate (at lower prices), or a combination of the two. Most importantly, they would improve the efficiency of the health-care sector, increasing funding available to treat patients.