Skip to main content
SpringerLink
Log in

A novel approach to prediction of welding residual stress and distortion

  • Research Paper
  • Published:
Welding in the World Aims and scope Submit manuscript

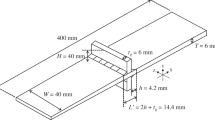
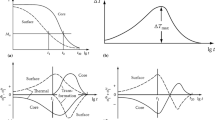
Abstract

A rigorous, accurate, and general methodology is presented to predict welding residual stress and distortion. The presented theory has two key advantages over existing experimental and numerical approaches: (1) there is an explicit relationship and dependency between input parameters and output values; and (2) it may be readily adapted to consider the effect of new and future processes, materials, and geometries. Formal definitions are provided and general formulae are derived for the two key attributes of the residual stress distribution: the material yield temperatures, and the tendon force. The yield temperatures are material properties which describe the respective boundaries of the plastic strain zone during heating and cooling. The tendon force corresponds to the net driving force for distortion. Practical engineering equations for each output value are presented as the combination of a minimal expression, based on idealized treatment, and correction factors to account for real life aspects not included in the ideal model. The idealized treatment corresponds to instantaneous line heating of an infinite thin section with constant material properties. Secondary phenomena considered expressly in this work include the following: incomplete uniaxial thermal constraint (i.e., the effect of welding procedure), temperature-dependent thermal and mechanical properties (i.e., the effect of material), and limited rigidity of a real cross-section with finite size and arbitrary shape (i.e., the effect of geometry). This work brings fresh insights to a century-old problem. The new contribution to knowledge includes both an improved theoretical understanding and also a practical consideration of how to apply this understanding to real-world, non-ideal problems of immediate and significant industrial relevance. This paper received the 2022 Henry Granjon award in Category C: Design and structural integrity and is based on work related to the author’s doctoral thesis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Okerblom NO (1955) (Transl. by London: HMSO, 1958). Raschet Deformatsii Metallokonstruktsii pri Svarke [The Calculations of Deformations of Welded Metal Structures]. Mashgiz, Moscow

  2. Tall L (1964) Residual stresses in welded plates - a theoretical study. Welding J 43(1):10s–23s

    Google Scholar 

  3. Kuzminov SA (1974) (In Russian). Svarochnie Deformazii Sudovich Korpusnich Konstrukzii [Welding Deformations of Ship Structures]. Sudostroenie, Leningrad

  4. White J (1977) Longitudinal shrinkage of a single pass weld. Univ. Cambridge Tech. Rep. CUED/C-Struct/TR.57

  5. Radaj D (1992) Heat effects of welding. Springer, Berlin

    Book  Google Scholar 

  6. Farkas J, Jármai K. (1997) Residual welding stresses and distortions. Analysis and optimum design of metal structures. CRC Press, London, pp 7–30

    Google Scholar 

  7. Gray T, Camilleri D, McPherson N (2014) Understanding welding distortion: thermal fields and thermo-mechanical effects. Control of Welding Distortion in Thin-Plate Fabrication. Woodhead Publishing Ltd., Cambridge, UK, Chap.4, 53–76

  8. Okano S, Mochizuki M (2015) Dominant factors and quantification of tendon force in welded structural materials. Trans. JSME [in Japanese] 81(830):15–00277

    Google Scholar 

  9. Doynov N, Stapelfeld C, Michailov VG, Pasternak H, Launert B (2019) Distortion analysis of large scaled welded structures. Math Model Weld Phenom 12:255–280

    Google Scholar 

  10. Dwight JB, Moxham KE (1969) Welded steel plates in compression. Struct Eng 47(2):49–66

    Google Scholar 

  11. Blodgett OW (1966) Joint design and production: control of shrinkage and distortion. Design of Welded Structures. The James F. Lincoln Arc Welding Foundation, Cleveland, OH, Chap.7.7

  12. Boulton NS, Lance Martin HE (1936) Residual stresses in arc-welded plates. Proc Inst Mech Eng 133(1):295–347

    Article  Google Scholar 

  13. Rodgers OE, Fetcher JR (1938) Determination of internal stress from the temperature history to a butt-welded plate. Welding J 17(11):4s–7s

    Google Scholar 

  14. Grams MR, Mendez PF (2022) Effect of compliance on residual stresses in manufacturing with moving heat sources. ASME J Appl Mech 89(2):021004

    Article  Google Scholar 

  15. Wells AA (1953) The mechanics of notch brittle fracture. Weld Res 7(2):34r–56r

    Google Scholar 

  16. Ueda Y, Fukuda K, Nakacho K, Endo S (1975) A new measuring method of residual stresses with the aid of finite element method and reliability of estimated values. Trans JWRI 4(2):123–131

    Google Scholar 

  17. Grams MR, Mendez PF (2021) Scaling analysis of the thermal stress field produced by a moving point heat source in a thin plate. ASME J Appl Mech 88(1):011001

    Article  CAS  Google Scholar 

  18. Grams MR, Mendez PF (2021) A general expression for the welding tendon force. ASME J Manuf Sci Eng 143(12):121002

    Article  Google Scholar 

  19. Mendez PF, Eagar TW (Oct. 2013) Order of magnitude scaling: a systematic approach to approximation and asymptotic scaling of equations in engineering. ASME J Appl Mech 80(1): 011009

  20. Greaves GN, Greer AL, Lakes RS, Rouxel T (2011) Poisson’s ratio and modern materials. Nat Mater 10(11):823–837

    Article  CAS  Google Scholar 

  21. Lu Y, Wang Y, Mendez PF (2020) Width of thermal features induced by a 2-D moving heat source. Int J Heat Mass Transfer 156:119793

    Article  Google Scholar 

  22. Lu Y, Mendez PF (2021) Characteristic values of the temperature field induced by a moving line heat source. Int J Heat Mass Transfer 166:120671

    Article  Google Scholar 

  23. The James F. Lincoln Arc Welding Foundation (2000) The procedure handbook of arc welding. 14th ed., Cleveland, OH

  24. Mendez PF, Tello KE, Lienert TJ (2010) Scaling of coupled heat transfer and plastic deformation around the pin in friction stir welding. Acta Mater 58(18):6012–6026

    Article  CAS  Google Scholar 

  25. Wang Y, Lu Y, Grams MR, Hintze Cesaro A, Mendez PF (2019) Asymptotics and blending in the modeling of welding. Math Model Weld Phenom 12:907–932

    Google Scholar 

  26. Grüneisen E. (1926) Zustand des festen körpers [the state of a solid body]. Julius Springer, Berlin. (Transl. by NASA 1959)

    Google Scholar 

  27. Stacey FD, Hodgkinson JH (2019) Thermodynamics with the Grüneisen parameter: fundamentals and applications to high pressure physics and geophysics. Phys Earth Planet Inter 286(1):42–68

    Article  Google Scholar 

  28. Belomestnykh VN, Tesleva EP (2004) Interrelation between anharmonicity and lateral strain in quasi-isotropic polycrystalline solids. Tech Phys 49(8):1098–1100

    Article  CAS  Google Scholar 

  29. Grams MR, Ludwig L, Mendez PF (2020) A quantitative index to assess the influence of joint fit-up on pipeline weld root discontinuities. Proc. ASME 13th Int. Pipeline Conf. (IPC2020-9706), p V003T05A032

  30. Satoh K (1972) Transient thermal stresses of weld heat-affected zone by both-ends-fixed bar analogy. Trans JWS 3(1):125–134

    Google Scholar 

  31. Satoh K, Toyoda M, Suita Y, Tanaka M, Hirano T (1986) Controlling parameters of residual stresses and deformations in welded thin cylindrical shells. Trans JWS 17(1):3–9

    Google Scholar 

  32. Ueda Y, Yuan MG (1993) Prediction of residual stresses in butt welded plates using inherent strains. ASME J Eng Mater Technol 115(4):417–423

    Article  Google Scholar 

  33. Yuan MG, Ueda Y (1996) Prediction of residual stresses in welded T- and I-joints using inherent strains. ASME J Eng Mater Technol 118(2):229–234

    Article  CAS  Google Scholar 

  34. Luo Y, Murakawa H, Ueda Y (1997) Prediction of welding deformation and residual stress by elastic FEM based on inherent strain (1st Report): Mechanism of inherent strain production. Trans JWRI 26 (2):49–57

    CAS  Google Scholar 

  35. Terasaki T, Nakatani M, Ishimura T (2000) Study of tendon force generating in welded joint. Q J Jpn Weld Soc [in Japanese] 18(3):479–486

    CAS  Google Scholar 

  36. Grams MR (2021) Predictive expressions for residual stress and distortion in welding and related thermal processes. PhD thesis, University of Alberta

  37. Rosenthal D (1941) Mathematical theory of heat distribution during welding and cutting. Welding J 20(5):220s–234s

    Google Scholar 

Download references

Acknowledgements

The author would like to acknowledge Simufact Engineering, part of Hexagon’s Manufacturing Intelligence division, for providing a license of Simufact Welding simulation software.

Funding

This work was partially supported by Enbridge Employee Services Inc. and the Natural Sciences and Engineering Research Council of Canada (NSERC) under a Collaborative Research and Development (CRD) grant no. 507483-2016.

Author information

Authors and Affiliations

  1. Department of Chemical and Materials Engineering, University of Alberta, 9211 116 Street NW, Edmonton, Alberta, T6G 1H9, Canada

    Mitchell R. Grams

Authors
  1. Mitchell R. Grams
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mitchell R. Grams.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Recommended for publication by Commission XV - Design, Analysis, and Fabrication of Welded Structures

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Grams, M.R. A novel approach to prediction of welding residual stress and distortion. Weld World 67, 1823–1832 (2023). https://doi.org/10.1007/s40194-023-01502-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40194-023-01502-w

Keywords

Search

Navigation