1 Introduction

The microstructure formed during welding and the heat-affected zone (HAZ) depend to a large extent on process parameters. The welded area is subjected to different thermal cycles, and thus different heating and cooling rates are achieved together with the maximum temperature in a given thermal cycle. In laser welding, this is influenced by the laser power, power density distribution, welding speed, and a number of thermal and physical properties such as the density, specific heat, thermal conductivity, and solidus and liquidus temperature of the welded steel. Knowledge of the influence of particular parameters and their combination is a prerequisite for obtaining a structure with the required properties.

Literature on the modelling of phase transformations occurring in steel in the laser welding process includes many examples in which the movement of liquid metal in the welding pool was not taken into account. Caron et al. [1] used the finite element method (FEM) to investigate the impact of different variants of continuous cooling transformation (CCT) diagrams on the calculated residual stresses. Only heat exchange equations were taken into account in the study, and only a quantitative dependence on experimental data was obtained. To take into account the heat exchange caused by the flow of liquid in the welding pool, the thermal conductivity of the welded material is artificially increased above the melting point [2,3,4]. The amount of heat supplied is decisive for the microstructure and mechanical properties in HAZ. The size and shape of the welding pool depend on the parameters of the heat source. To simplify, Goldak’s heat source model [5] was assumed, together with the calibration of the model consisting in adjusting parameters of the front and rear quadrant of the source ellipsoid in such a way as to obtain the best possible fit with the experiment [6,7,8,9,10]. In the case of full penetration welds, there were attempts to make up for the omission of the fluid flow in the welding pool by modelling a heat source in the shape of a double cone [11].

The Peclet number (Pe) is the parameter which proves the significance of the influence of convective heat exchange in the welding pool. Convection in the melted zone influences its size and shape [12, 13]. Therefore, preliminary assessment of the Peclet number value is crucial for determining the correctness of the assumed assumptions simplifying the model. The value of the Peclet number significantly exceeding unity indicates the dominant influence of convection in the heat exchange in the welding pool.

Weldability, understood as the ability to form welds with the required physical properties, largely depends on the phase structure in the weld area and heat-affected zone. The welded material is subjected to thermal cycles which are characterised by different heating and cooling rates and maximum temperature achieved in the thermal cycle. Knowledge of the thermal cycles for the individual HAZ points allows us to predict the order of phase changes during cooling. Quantitative analysis of the transformation kinetics is done based on the decomposition diagram of undercooled austenite in welding conditions (CCT-W - continuous cooling transformation diagram in welding conditions). The CCT-W diagram differs from the CCT diagram [14]. The difference results from the conditions prevailing in the welding process in comparison to traditional heat treatment. Among other things, a much higher austenitisation temperature is achieved during welding, holding time at the austenitisation temperature is shorter, and high cooling rates are reached. Dilatometry is one of the methods to generate the CCT curves. The method is based on measurement of the volume change caused by the transformation and differences in the characteristics of thermal expansion of phases [15]. During thermal processing, the material is subjected to heating and cooling cycles, which are accompanied by changes in its microstructure [16,17,18]. Due to high heating and cooling rates and the formation of a liquid phase, welding requires a number of specific conditions to be taken into account, such as enforcing convection in the welding pool by the Marangoni effect [19] and interaction between the laser beam with the welded material [20]. Welding process modelling allows us to calculate the size and shape of the fusion zone (FZ) and HAZ. The thermal cycles in the FZ and HAZ are used to calculate the volume fraction of the microstructural components forming there. The development of a mathematical welding model provides an opportunity to choose welding parameters, such as the power of the heat source, laser beam radius, or welding speed, in order to obtain a structure with the required properties for the selected weld material and geometry.

Many publications on the modelling of the welding process do not take the momentum equation into account. This approach is justified by speeding up computations. However, this necessitates making assumptions based on measurements and adjusting the model parameters. This significantly affects the accuracy and reliability of the model. The paper takes into account the energy and momentum conservation equations for laser welding. The model proposed in this paper applies to the spot and continuous laser welding. For the given parameters of the laser beam and material data, the model shows evolution of the weld pool and flow diagram of the liquid. The model predicts phase changes during cooling and the final phase composition in the FZ and the HAZ. Input data include, among others, thermal and physical data of welded material as well as laser beam parameters. To test how the phase change model works, S335J2 steel as the example material was used. The small size of the individual zones in the welding area hinders direct measurements of their structural and mechanical properties. Therefore, computer simulation of the welding process is an important tool for analysing many processes such as heat and mass flow and phase changes. This paper leaves out the issues related to stress and deformations caused by heating, cooling, and phase changes.

2 Phase change model

The phase change model includes a prism-shaped sample sized 2×5×2 mm. A schematic view of the welding process described in this paper is shown in Fig. 1. The source of welding heat includes a laser beam moving at a constant speed along the welding line or fixed in an immobile manner above the sample. Due to the symmetrical nature of the modelled process, only half of the welding area was covered by calculations (limited by the symmetry area). The formation and development of the welding pool and the quality of the joint are significantly influenced by the distribution of the laser beam intensity [21]. The model uses a laser beam mode TEM10 used for welding, whose power density distribution is described in the equation:

$$ I(r)=\frac{2P}{{\pi a}^2}{\left[1-2{\left(\frac{r}{a}\right)}^2\right]}^2\exp\ \left[-2{\left(\frac{r}{a}\right)}^2\right] $$
(1)

where P is the laser power, a is the laser beam radius, and r is the distance from the laser beam axis.

Fig. 1
figure 1

Schematic drawing of a welding process model sized 2×5×2 mm

Full size image

Part of the laser energy falling on the upper surface of the model (Fig. 1) is reflected, while the remaining part penetrates the material and is absorbed by it. For the sake of simplicity, the material absorption coefficient (α) was assumed to be constant. The model uses a volumetric welding heat source. The heat source model is based on the Beer-Lambert law, which describes the local contribution to the heat source according to the following equation:

$$ \dot{Q}\left(r,z\right)=\eta\ I\ (r)\upalpha \exp \left(-\upalpha z\right) $$
(2)

where η is the absorption coefficient of the surface and z is the distance from the surface illuminated by the laser beam.

During welding, a welding pool is formed in the area affected by the laser beam. In the paper, it was assumed that for the applied laser power, the welding pool surface remains flat. Parts of the energy absorbed by the welded sample are transmitted to the environment through convection, radiation of the heated surface, and the evaporation of liquid steel. The energy balance on the free pool surface is described by the following equation:

$$ -k\frac{\partial T}{\partial \overrightarrow{n}}=\eta\ I\ (r)-h\left(T-{T}_a\right)-\sigma \varepsilon \left({T}^4-{T}_a^4\right)-{q}_{evap} $$
(3)

where k is thermal conductivity, \( \overrightarrow{n} \) the unit vector normal to the plane, h is the convective heat transfer coefficient, σ is the Stefan-Boltzmann constant, ε is surface emissivity, T and Ta are the surface and ambient temperature on an absolute scale, and qevap is heat loss due to evaporation.

On other walls, not illuminated by the laser beam, the energy is dissipated to the environment by convection and radiation as described by the formula:

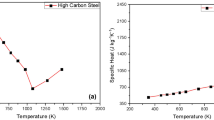
$$ -k\frac{\partial T}{\partial \overrightarrow{n}}=-h\left(T-{T}_a\right)-\sigma \varepsilon \left({T}^4-{T}_a^4\right) $$
(4)

Tables 1 and 2 present nominal composition and material data on S355J2 steel (according to EN 10025-2:2004) [22] and laser beam parameters used in the calculations. In the semi-liquid zone of the welding pool, for temperatures between solidus and liquidus, the material data are calculated as a linear interpolation of the solid and liquid values. The distribution of laser power density described by Eq. (1) is a function of the distance from the laser beam axis. The laser beam energy is strongly concentrated in the laser axis and the ring around this axis. In this way, the welding pool surface is heated unevenly. The highest temperature is achieved near the laser beam axis. This creates a Marangoni effect on the welding pool surface, with a force tangential to the poll surface, forcing the flow of liquid steel into the pool. The direction of the circulation of liquid steel depends on the temperature gradient on its surface and the content of surface-active elements [24].

Table 1 Chemical composition of S355J2 steel (wt%)
Full size table
Table 2 Material data used for the calculations for the S355J2 steel welding model [2, 21,22,23]
Full size table

In the described model, the dependence of the shear stress \( {\tau}_{\overrightarrow{s}} \) on the temperature of the weld pool free surface, in the direction tangential to the surface, is described by the formula [25, 26]:

$$ {\tau}_{\overrightarrow{s}}={\mu}_l\frac{\partial \left(\overrightarrow{V}\cdot \overrightarrow{s}\right)}{\partial \overrightarrow{n}}={f}_l\frac{\partial \gamma }{\partial T}\frac{\partial T}{\partial \overrightarrow{s}} $$
(5)

where \( \overrightarrow{V} \) is the liquid velocity vector, \( \overrightarrow{s} \) and \( \overrightarrow{n} \) are the unit vectors tangential and normal to the weld pool free surface, μl is the dynamic viscosity of liquid steel, fl is the liquid volume fraction, and γ is the surface tension coefficient. The shear stress given by Eq. (5) forces the liquid on the surface to move, therefore also causing movement in the whole volume of the welding pool. The model assumes that the weld pool surface remains flat during welding.

The surface tension of liquid steel depends on the temperature and the concentration of surface-active elements, as described in the formula [23]:

$$ \gamma ={\gamma}_m^{{}^{\circ}}-A\left(T-{T}_m\right)- RT{\Gamma}_S\ln \left[1+{k}_1{c}_i{e}^{-\left(\Delta {H}^{{}^{\circ}}/ RT\right)}\right] $$
(6)

where \( {\gamma}_m^{\circ } \) is the surface tension of the pure metal at the melting point, A is the negative value of the ∂γ/∂T for pure metal, Tm is the melting temperature, Γs is the surface excess of the element at the point of saturation, k1 is a constant depending on the entropy of the segregation, ci is the concentration of the surface-active element, and ΔH∘ is standard heat of adsorption.

The temperature-depended surface tension coefficient ∂γ/∂T in (5) is calculated by differentiating Eq. (6) with respect to temperature:

$$ {\displaystyle \begin{array}{c}\frac{\partial \gamma }{\partial T}=-A-R{\Gamma}_S\ln \left[1+K{c}_i\right]-\frac{K{c}_i}{\left(1+K{c}_i\right)}\frac{\Gamma_S\Delta {H}^{{}^{\circ}}}{T}\\ {}K={k}_1{e}^{-\left(\Delta {H}^{{}^{\circ}}/ RT\right)}\end{array}} $$
(7)

In this paper, the temperature-depended surface tension coefficient is the function of temperature only. For pure metal, the ∂γ/∂T coefficient is negative, but the increase in the concentration of surface-active elements (e.g. sulphur, oxygen) changes its sign to positive [23]. This forces a change in the liquid flow direction. The direction of heat transport also changes, and therefore the shape of the welding pool is different for these two cases [24]. The data for the calculation of the temperature-depended surface tension coefficient is presented in Table 2.

The solution to the welding process model described above consists in calculating the thermal and velocity fields, for the given initial and boundary conditions in each time step. It is therefore necessary to solve the energy, momentum, and mass conservation equations. The task was carried out using the Ansys Fluent software package for the computational fluid dynamics (CFD) modelling. The software uses the finite volume method (FVM) to solve the liquid flow and heat transfer equations for complex geometries [27]. With the Ansys Fluent package, a model of the calculation area, sized 2×5×2 mm, was constructed (Fig. 1) and divided with a cubic grid. To achieve a stable and accurate solution, a heterogeneous grid was used. In the area directly affected by the laser, the grid was denser, with a cell size of 0.005 mm. In the areas far away from the laser axis, the average cell size was 0.3 mm. The predicted value of the Reynolds number in the modelled welding process exceeds 500. Thus, the standard turbulent model k-ε [27] was chosen for flow calculations in the Fluent package. A volumetric heat source (Eq. (2)) was added to the energy conservation equation, and it was defined using the user-defined functions (UDF) in Fluent. UDF was also used to introduce the boundary conditions described by Eqs. (3) and (4) and boundary conditions for energy and momentum conservation by Eqs. (5–7).

During welding, the laser beam supplies energy to the subsequent areas of the welded pieces, causing them to fuse. Depending on the distance from the heat source, initial and boundary conditions, and thermal and physical data of the material, individual computational points in the model are subjected to different thermal cycles. During the heat-up phase of the thermal cycle, the original steel structure begins to change into austenite once the temperature for starting the austenitic transformation Ac1 is exceeded. When the temperature reaches the end temperature for austenitic transformation Ac3, the volume fraction of austenite reaches unity. The formation of austenite is a diffusive process, strongly dependent on the heating rate. The beginning and end temperature for austenitic transformation was calculated based on [28]. To calculate the volume fraction of austenite during heating XA, the following linear interpolation was used:

$$ {X}_A(T)=\left\{\begin{array}{ccc}0& & T\le {A}_{c1}\\ {}\frac{T-{A}_{c1}}{A_{c3}-{A}_{c1}}& {A}_{c1}<& T<{A}_{c3}\\ {}1& & T\ge {A}_{c3}\end{array}\right. $$
(8)

where Ac1 and Ac3 depend on the heating rate vh [28].

During welding, each HAZ point in its thermal cycle reaches its maximum temperature, which is followed by a cooling stage. During cooling, austenite breaks down into phases, whose order of formation depends on the chemical composition of the steel and the cooling rate. Phase changes during steel cooling can be divided into diffusive and diffusionless.

Diffusive phase changes in steel, such as ferritic, perlite, and bainitic, are described by the Johnson-Mehl-Avrami-Kolmogorov (JMAK) equation [29]. According to this equation, the progress of the i-th phase change during continuous cooling can be calculated using the function:

$$ {X}_i^j={\hat{X}}_A{\overset{\check{} }{X}}_i\left(1-\exp \left(-b(T){t_j}^{n(T)}\right)\right) $$
(9)

where \( {X}_i^j \) is the volume fraction of the i-th phase in the j-th time step, \( {\hat{X}}_A \) is the volume fraction of austenite formed during heating, \( {\overset{\check{} }{X}}_{\mathrm{i}} \) is the maximum fraction of the i-th phase formed for a given cooling rate determined from the CCT diagram, and b(T) and n(T) are coefficients dependent on steel, calculated from the following equations:

$$ b(T)=\frac{-\ln \left(1-{X}_s\right)}{t_s^{n(T)}} $$
(10)
$$ n(T)=\frac{\ln \left\{\frac{\ln \left(1-{X}_s\right)}{\ln \left(1-{X}_f\right)}\right\}}{\ln \left(\frac{t_s}{t_f}\right)} $$
(11)

where ts and tf are the start and finish time of the phase change when the initial Xs and final Xf volume fraction are 0.01 and 0.99, respectively.

After cooling below temperature Ms, diffusionless martensitic transformation occurs. The martensitic transformation is described by the Koistinen-Marburger equation [30]:

$$ {X}_i={\hat{X}}_A{\overset{\check{} }{X}}_M\left(1-\exp \left(-k\left({M}_s-T\right)\right)\right) $$
(12)

where \( {\overset{\check{} }{X}}_{\mathrm{M}} \) is the maximum fraction of martensite formed during cooling at a given cooling rate, determined from the CCT diagram, and k is a coefficient calculated from Eq. (12) for the temperature of the start Ms and the finish Mf of the martensitic transformation determined from the CCT diagram:

$$ k=\frac{-\ln \left({X}_s\right)}{M_s-{M}_f} $$
(13)

where Xs is the initial volume fraction of martensite equal to 0.01.

The volume fraction of austenite formed at a given HAZ computational point during heating \( {\hat{X}}_A \) is calculated based on the maximum temperature Tpeak for a given thermal cycle using the formula:

$$ {\hat{X}}_A={X}_A\left({T}_{peak}\right) $$
(14)

At each point of the heat-affected zone, the welded material is subjected to thermal cycles. The thermal cycle is described by the shape of the heating and cooling curve and Tpeak temperature. A highly concentrated heat source, such as a laser, heats up the material causing its local fusion. The shape of the thermal cycle at each point of the weld and heat-affected zone has a decisive influence on the final phase composition, mechanical properties, and stresses in the HAZ. The heating and cooling rate and the maximum temperature reached during welding (Tpeak) depend on, among others, the thermal conductivity of the steel, shape of the welded workpiece, distance from the axis of the weld, and the welding line energy El described by the equation:

$$ {E}_l=\frac{\eta P}{\upsilon } $$
(15)

where v is the welding speed.

The described phase change model assumes that welding takes place in one pass, with a single laser beam moving at a constant speed. In such a case, in the cooling phase of the thermal cycle, the cooling rate decreases with time. Therefore, the fraction of phases generated during the cooling stage in the heat-affected zone is determined from the value of the average cooling rate in the 800–500°C temperature range, calculated from the formula:

$$ {\upsilon}_{8/5}=\frac{800{}^{\circ}C-500{}^{\circ}C}{t_{8/5}} $$
(16)

where t8/5 is the cooling time in the 800–500°C temperature range.

The resulting welded joint consists of native material, the HAZ, and weld. The size of these zones matters due to the differences in microstructure and thus their mechanical properties. For most steels, the base material is the area of the joint where no changes take place and where the Tpeak temperature does not exceed 500°C. Due to phase changes, the heat-affected zone has a more complex structure in unalloyed and low-alloy steels. The division of the heat affected area is just a matter of convention, as the transition between them is smooth and depends on the maximum temperature at which the area is formed:

  • Fused—at a temperature higher than the liquidus temperature (Tliq)

  • Partially fused—for the temperature between the solidus (Tsol) and the liquidus

  • Superheated—at a high temperature of 1100°C–Tsol where austenite grains break down and the structure exhibits low plasticity and impact strength

  • Normalised—in the Ac3–1100°C range where a fine-grained, high plasticity structure emerges

  • Incomplete normalised—in the Ac1–Ac3 range, where austenite is formed only from a part of perlite, and plasticity levels after cooling are high

  • Recrystallised—in the 500°C–Ac1 range, where the steel subjected to cold plastic deformation is recrystallised to increase its plasticity

In this model, the position of each zone is determined by the formula:

$$ {C}_{st}=f\left({T}_{peak}\right) $$
(17)

where Cst is the parameter describing the state of the structure in a given model position after cooling.

Figure 2 presents the algorithm for prediction of the phase changes occurring during heating and cooling. The algorithm has been implemented in C language as a series of UDF’s, compiled to the shared library and loaded into Fluent at runtime. Input data for the algorithm include temperature field, in the current (Tn), and the previous (Tn1) time step. For each time step, the algorithm iterates overall cells of the computational domain, calculating the heating and cooling rate (vT). Phase change parameters calculated for the model cells are stored in user-defined memory (UDM) until another iteration is completed.

Fig. 2
figure 2

Block diagram of the phase change algorithm defined by the UDF function

Full size image

The algorithm starts with computing vT in each cell. Execution of one of two main branches of the algorithm depends on the sign of vT. During heating (vT > 0), the volume fraction of austenite (XA) and the cell’s maximum temperature Tpeak are calculated. During the cooling stage (vT < 0) in the 800–500°C temperature range, the average cooling rate v8/5 necessary to determine the sequence of changes and their parameters is calculated. Once the grid cell enters the time and temperature range of a given phase change (i), in subsequent time steps, the volumetric fraction of the phase (Xi) formed from cooled austenite is calculated.

The Ansys Fluent software package used here solves the energy conservation equation in the form [27]:

$$ \frac{\partial \left(\rho E\right)}{\partial t}+\nabla \cdotp \left(\overrightarrow{\upsilon}\left(\rho E+p\right)\right)=\nabla \cdotp \left({k}_{eff}\nabla T+\overset{=}{\tau}\cdotp \overrightarrow{\upsilon}\right)+{S}_h $$
(18)

where E is energy (E = h − p/ρ + 0.5v2), h is enthalpy, p is pressure, keff is effective thermal conductivity (keff = k + kt), kt is turbulent thermal conductivity, \( \overset{=}{\uptau} \) viscosity tensor, and Sh is the volumetric heat source.

The austenite phase changes in steel during continuous cooling are accompanied by heat generation. In the model, for each cell in which cooled austenite phase change takes place, the volumetric heat source for the i-th phase formation is calculated, \( {\dot{q}}_{v,i} \) from the equation:

$$ {\dot{q}}_{\upsilon, i}=\Delta {H}_i\frac{\Delta {X}_i}{\Delta t}\rho $$
(19)

where ΔHi is the enthalpy of i-th phase formation from undercooled austenite [31], ΔXi is the volume fraction increase of i-th phase in time step Δt, and ρ is steel density. The heat of the i-th phase change occurring at the cooling stage \( {\dot{q}}_{v,i} \) is added using UDF to the heat source Sh in Eq. (18).

The algorithm ends when the temperature of all the cells drops below the end temperature for the last phase change resulting from the CCT diagram.

3 Results of phase change model calculations

The operation of the phase change algorithm was tested using the welding model, whose outline is shown in Fig. 1. Tests have been carried out for a moving (A) and fixed (B) laser beam. In case (A), a 3 kW laser and two welding speeds were used: 1.0 m/min and 1.5 m/min. The total welding time (toff) was 0.12 s and 0.08 s, respectively. The welding time was chosen in such a way that the depth of the welding pool does not increase in the final welding phase. For case (B), two laser beam power of 3 kW and 5 kW were used. In this case, the laser beam heated the sample for 0.1 s. In this case, the heating time was selected in such a way that the fused zone did not reach deeper than about ½ of the model height. For both cases, the tests ended when all grid cells, which met the condition Tpeak > Ac1 during the heating phase, cooled below the end temperature for the last of the predicted phase changes.

Each of the tests consists of a heat-up phase followed by a cooling phase. In the first welding phase, the material is heated to a temperature higher than the fusion temperature. The Marangoni effect acting on the surface of the created welding pool causes the liquid to flow in the direction of the laser beam axis and then to the interior of the welding pool. Figures 3 and 4 show the distribution of the velocity field in the cross-section passing through the laser axis and the welding line. Both figures are in same scale. The circulation direction of the liquid steel, which is formed during welding, forces the transport of the heated liquid to the bottom of the welding pool. The liquid moving downwards cools down and then flows upwards in the outer areas of the welding pool. This circulation pattern of the liquid creates a deep and narrow welding pool.

Fig. 3
figure 3

Velocity field distribution vmag (m/s) after time t = 0.048 s for a sample welded with the following parameters: (a) P = 3 kW, v = 1 m/min, and (b) P = 3 kW, v = 1.5 m/min. The figure shows an outline of the grid on the upper surface and the model symmetry plane. The scale of the drawing applies only to the welding line within the marker range

Full size image
Fig. 4
figure 4

Velocity field distribution vmag (m/s) after time t = 0.096 s for a sample spot welded with the following parameters: (a) P = 3 kW and (b) P = 5 kW. The figure shows an outline of the grid on the upper surface and the model symmetry plane. The scale of the drawing applies only to the welding line within the marker range

Full size image

For the assumed welding parameters and material data, very high cooling rates were achieved in the welding area and HAZ. Figures 5 and 6 show the temperature variation graphs at a distance of 1.5 mm from the beginning of the welding line for case (A). Point p0 lies on the surface of the sample, and subsequent points are evenly spaced down to a depth of 1 mm. For the moving heat source (Fig. 5), for point p0 lying on the surface of the sample, there is a double maximum observed on the temperature curve. The shape of the power density profile used as described by Eq. (1) and the direction of circulation of the liquid supplying heat to the outer areas of the welding pool contribute to the creation of this secondary maximum. This effect becomes less and less visible as the distance between the measuring point and the surface increases. In case (B), where the laser does not move, the temperature variation curves only have one maximum (Fig. 6). For points that reach a temperature exceeding solidus during the heating phase, immediately after switching the laser off (toff = 0.1 s) for a short period, they cool down more slowly thanks to the circulation of the residual liquid phase.

Fig. 5
figure 5

Thermal history of measurement points at a distance of 1.5 mm from the beginning of the welding line, for a sample welded with the following parameters: (a) P = 3 kW, v = 1 m/min, and (b) P = 3 kW, v = 1.5 m/min. Point p0 lies on the surface of the sample, and subsequent points are evenly spaced down to a depth of 1 mm

Full size image
Fig. 6
figure 6

Thermal history of measurement points in the laser beam axis, for a sample spot welded with the following parameters: (a) P = 3 kW and (b) P = 5 kW. Point p0 lies on the surface of the sample, and subsequent points are evenly spaced down to a depth of 1 mm

Full size image

In the phase change algorithm applied (Fig. 2), the average cooling rate in the temperature range 800–500°C (v8/5) is calculated in the cooling phase. For selected measurement points (Figs. 5 and 6), the cooling rate achieved in the cooling phase was 1.4–2.2*104 K/s in case (A) and 0.7–1.9*104 K/s in case (B). For such cooling rates of S355J2 steel, according to the CCT diagram [1], martensite is the only phase forming from undercooled austenite. Figures 7 and 8 present the kinetics of the phase composition change of the measuring point p0 in the cooling phase for the investigated welding cases.

Fig. 7
figure 7

Volume fraction history of measurement point p0 for a sample welded with parameters: (a) P = 3 kW, v = 1 m/min, and (b) P = 3 kW, v = 1.5 m/min

Full size image
Fig. 8
figure 8

Volume fraction history of measurement point p0 for a sample spot welded with parameters: (a) P = 3 kW and (b) P = 5 kW

Full size image

In case (A), welding with a moving heat source, the formation of the martensitic phase starts before the welding is completed (toff). The martensitic transformation starts where the welding line starts. At the same time, the laser beam moves towards the end of the welding line (Fig. 9). In case (B), the cooling phase takes place after the laser is switched off. When the laser is switched off once toff elapses, it is quickly cooled down to a temperature where the martensitic transformation starts in the area directly affected by the laser (Fig. 10). In both welding cases, martensite starts forming in the outer HAZ areas. As the cooling progresses, the martensitic transformation start zone approaches the welding line.

Fig. 9
figure 9

Martensite phase field (%) for a sample welded with parameters: (a) P = 3 kW, v = 1 m/min, toff = 0.12 s after time t = 0.156 s, and (b) P = 3 kW, v = 1.5 m/min, toff = 0.08 s after time t = 0.096 s. The figures show a grid outline on the upper surface and the model’s symmetry plane. The scale of the drawing applies only to the welding line within the marker range

Full size image
Fig. 10
figure 10

Martensite phase field (%) for a sample spot welded with parameters: (a) P = 3 kW, toff = 0.1 s after time t = 0.126 s, and (b) P = 5 kW, toff = 0.1 s after time t = 0.156 s. The figures show a grid outline on the upper surface and the model’s symmetry plane. The scale of the drawing applies only to the welding line within the marker range

Full size image

4 Summary and conclusions

The paper presents a model of the laser welding of steel. The model accounts for welding parameters and material data. The usefulness of the proposed model for welding of S355J2 steel with selected welding parameters was investigated. The model allows for tracking the progress of phase transformations during welding and the subsequent cooling stage. Two cases of spot and continuous welding were tested on a rectangular prism sample. The proposed welding model was implemented in the Ansys Fluent software package, with the boundary and initial conditions described in the paper. With the UDF, it was possible to implement the proposed phase change algorithm. For welding conditions used in the model, only the martensitic phase was created. Short welding times of the sample caused the formation of a large temperature gradient and cooling rates exceeding critical levels.

The S355J2 steel used in the model belongs to the low-carbon grade which is readily weldable. In the single-pass bead-on-plate tungsten inert gas (TIG) welding process [32] welded at speed of 3 mm/s, power of 3.3 kW, and heating radius 8 mm, the predominant phase in FZ is bainite with martensite scattering in it. The base material is still the mix of ferrite and pearlite because the peak temperature does not exceed the Ac1. In the model described in this article, welding speed is much higher (17 mm/s) and a much smaller radius of the heat source (0.4 mm). As a result, the heat flux supplied for welding is much higher than in [32], and the cooling rates are much higher. A single-pass complete-penetration gas metal arc (GMA) welding was conducted in the welding simulation [6] at power of 7.9 kW and welding speed 6.7 mm/s. Resulted the final microstructure comprises 94% bainite and 6% ferrite and pearlite. Welding line energy for reference [6] was about 1.1 kJ/mm, i.e. over ten times greater than in the model described here. At a distance of 9 mm from the welding centreline, the value t8/5 = 38 s [6]. In the article, the area where the peak temperature exceeds the Ac1 temperature in the direction perpendicular to the welding direction is 0.8 mm (Fig. 9). A similar value of the welding line energy 1.7 kW/mm was used in the reference [33]. The empirical phase percentages referring to a node at the middle of FZ were 49% bainite and 51% ferrite and pearlite. As can be seen from the above comparisons with references [6, 32, 33], a lower value of welding line energy with a much higher energy flux consequently results in cooling rates favouring the formation of martensite in the FZ.

The tests performed have shown that for the accuracy of the phase change model, it is important to take into account the surface tension in the welding pool. In steel, the surface tension in the welding pool forces the circulation of fluids, which promotes deep fusion. Simplification of the welding model by omitting the momentum conservation equation or using artificial thermal conductivity values in the liquid phase only takes into account the transfer of welding energy by conduction. The amount of energy supplied to the welding area and the shape of the fusion zone depend only on the assumed conductivity coefficient value and the power density distribution function of the laser beam. In the proposed model, for welding other steel grades, the value and sign of the (∂γ/∂T) coefficient, depending on the concentration of surface-active element and temperature, may force a different fluid circulation pattern. This will definitely change the size and shape of the fusion zone and the HAZ. For the steel and welding conditions applied, the Peclet number was ~100. This proves the definite convective advantage of heat exchange. The convective flow of steel in the liquid phase boosts heat exchange in the welding pool.

In the proposed model, the data describing the shape of the beginning and end of phase change diagram for continuous cooling of the tested steel are read from data files by UDF. Thus, the proposed model can be used for other steels as well as for the welding of steels with different chemical compositions.

The model proposed in this study proves importance of CFD in modelling of metallurgical processes during welding. A model in which, in addition to the heat conduction equations, the turbulent fluid flow equations are also solved is computationally intensive. Solving additional equations for the velocity field, pressure, turbulent kinetic energy, and rate of dissipation of turbulent kinetic energy greatly extends the computation time. Additionally, the solution convergence condition requires a significant increase of the computational grid density in the FZ. The advantage of CFD modelling is the ability to model the fluid flow which is important for prediction of the FZ shape and the phase changes in the HAZ.