Abstract
Purpose of Review
Computational and mathematical modeling have become a critical part of understanding in-host infectious disease dynamics and predicting effective treatments. In this review, we discuss recent findings pertaining to the biological mechanisms underlying infectious diseases, including etiology, pathogenesis, and the cellular interactions with infectious agents. We present advances in modeling techniques that have led to fundamental disease discoveries and impacted clinical translation.
Recent Findings
Combining mechanistic models and machine learning algorithms has led to improvements in the treatment of Shigella and tuberculosis through the development of novel compounds. Modeling of the epidemic dynamics of malaria at the within-host and between-host level has afforded the development of more effective vaccination and antimalarial therapies. Similarly, in-host and host-host models have supported the development of new HIV treatment modalities and an improved understanding of the immune involvement in influenza. In addition, large-scale transmission models of SARS-CoV-2 have furthered the understanding of coronavirus disease and allowed for rapid policy implementations on travel restrictions and contract tracing apps.
Summary
Computational modeling is now more than ever at the forefront of infectious disease research due to the COVID-19 pandemic. This review highlights how infectious diseases can be better understood by connecting scientists from medicine and molecular biology with those in computer science and applied mathematics.
Similar content being viewed by others
Introduction
Infectious diseases are caused by organisms or pathogens (bacteria, viruses, fungi, or parasites). The symptoms and etiology of infectious diseases vary widely, and this translates to vastly different treatments and case fatality ratios. As such, different approaches are needed to combat each disease, putting a strain on public health resources. Mathematical and computational modeling have long been employed to combat infectious diseases and improve the understanding of their development, dispersion, and treatment [1], with techniques applied to modeling one disease being largely translatable to another. The first application of mathematical modeling in infectious diseases arose in 1766, when Daniel Bernoulli developed a mathematical model to analyze the mortality rate of smallpox [2]. Since then, the field of epidemiological modeling has expanded to encompass models of varying complexity accounting for a multitude of scales, including within-host pathogen dynamics [3•, 4] and social, economic, and demographic host-host dynamics [5, 6].
Infectious disease models have been used to better understand and predict contagion dynamics ranging from the intracellular level to the within-host scale to between-host interactions (Fig. 1). Mathematical modeling allows for the integration of a mechanistic understanding of biological processes into precise and logical structures [7]. A correctly specified mathematical model reproduces observed empirical patterns and enables predictions of the impact of changing conditions on real-world outcomes [7]. Many techniques are used to model infectious diseases, including multiscale models [8], stochastic modeling [9], game theory [10], continuous single- or multi-variable models [11], and, more recently, machine learning and artificial intelligence [12]. Modeling therefore plays a crucial role for predicting, assessing, and controlling potential outbreaks [2] and offers practically useful means for policy makers to evaluate the potential effect of intervention strategies [9].
Modeling infectious diseases occurs at multiple scales. At the intracellular scale, models have been used to understand the pathobiology of infectious pathogens, their replication, and within-host cellular dynamics so that more effective and targeted treatments may be developed. Left panel: Agent-based models can be used to model intracellular dynamics where the probability of infection is a function of receptors r and the movement of pathogens can be described as discrete lattice jumps with a given probability pi, j. Center panel: A large majority of infectious diseases cause a significant systemic reaction and can be captured at both the tissue- and systemic-level by in-host models. ODE systems where target cells (T), infected cells (I), and virus (V) modeling infection, replication, and cell death have been used to understand within-host dynamics. Right panel: At the population level, the spread of infectious diseases within a local community to the global scale is crucial to our understanding of how diseases can be stopped and pandemics prevented. Similar modeling systems to within-host models can be used to model disease epidemiology where susceptible individuals (S) become infected (I) and then eventually recover (R)
Although infectious vectors are unique, most between-host dynamics are modeled using the susceptible-infected-recovered (SIR) model [13, 14]
where S(t), I(t),and R(t) are the number of susceptible, infected, and recovered individuals at time t, β is the transmission rate, and k is the recovery rate. Extensions of the SIR model have proven useful to study the spread of dengue [15], malaria [16], and SARS-CoV-2 [17], among others. Stochasticity can be incorporated by describing disease spread progression by a chain binomial model, where the number of susceptible members St + Δt at time t + Δt is a binomial random variable depending on St, It and the recovery rate [9]. This highly versatile SIR approach has also inspired mathematical investigations of disease dynamics within the host. Existing reviews of within-host modeling have described in depth the extensive roles that mathematical models have played in elucidating effective immune responses to viruses and bacteria [18,19,20], improving drug or therapeutics treatments [21], and informing the design of vaccines [22, 23] to protect against pathogens.
Here we survey numerous recent examples to demonstrate the modern reach of modeling of infectious diseases caused by bacteria, parasites, and viruses. We discuss specific examples at different scales where state-of-the-art research employing mathematical and computational modeling, bioinformatics, machine learning, and artificial intelligence was used.
Bacteria
Developing novel ways to treat bacterial pathogens often requires multifaceted, synergistic approaches. We highlight as examples recent impactful research into the infectious dynamics of Shigella and Mycobacterium tuberculosis and the ever pressing issue of antibiotic resistance.
Shigella
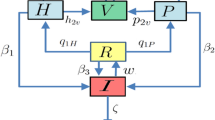
The ongoing effort to design a safe and effective vaccine against Shigella, a deadly dysentery-causing bacterium, has not yet produced a licensed compound despite decades of laboratory work and clinical trials. Fundamentally understanding the underlying immune correlates of protection is considered crucial to success in vaccine design [24, 25], and two distinct mathematical approaches have been applied to identify key immune interactions from Shigella vaccine trials and human challenge studies. Arevalillo et al. [26] used a random forest machine learning algorithm, classification and regression trees (CART), and statistical approaches to determine that immunoglobulin-G (IgG) antibody in the blood and immunoglobulin-A (IgA) antibody-secreting cells correlate with immune protection against Shigella. Davis et al. [3•, 27] built mechanistic differential equation models of the gut immune response to Shigella in humans (Fig. 2a) and concluded that antibody-based vaccines that target lipopolysaccharide or proteins on Shigella’s outer membrane are unlikely to sufficiently protect against severe disease, deploying sensitivity analysis to identify other possible targets for further study.
Within-host and between-host modeling of bacterial infections. (a) Davis et al. [3•] developed a model for the key interactions between Shigella and the host’s humoral immune system using a detailed ODE system represented in their schematic. The distinction between bacterial pathogenesis (blue) and antibody and B cell dynamics (red) is denoted in a biological representation (left) and in the mathematical model (right). Prior to infection of epithelial cells, Shigella, S, can be removed by antibodies IgA, A, IgG, and G or engulfed by macrophages. Reprinted open access [3•]. (b) Salvatore et al. [32] developed a method to study drug resistance-associated mutations from Mycobacterium tuberculosis strains causing multiple cases in a household. Households were matched by the number of antibiotics to which the household strain was resistant, the number of household contacts and the follow up time. Their case-control design presents a useful approach for assessing in vivo fitness effects of drug resistance mutations. Reprinted with permission from [32]
Mycobacterium tuberculosis
Infection with Mycobacterium tuberculosis is the precursor to tuberculosis (TB) disease and is responsible for more deaths than any other infectious diseases, some 1.5 million per year [28]. Until recently, one-third of the population was thought to be carrying a latent TB infection. Houben and Dodd [28] sought to quantify the true proportion of latent infections by constructing trends in annual risk in infection (ARI) using a combination of direct ARI estimates and Gaussian process regression to represent data uncertainty and any years without data. Their estimate of the global burden of latent TB infection was 23%, in contrast to the commonly cited proportion of one-third.
Given the latent TB burden, drastic changes are required to achieve the 2050 target of complete elimination of TB [29]. The renewed urgency to develop effective treatments for TB infection has resulted in large-scale phenotypic screens that led to thousands of new compounds with activity in vitro [30•]. While promising, a major obstacle is identifying compounds worthy of in vivo clinical investigation. The careful curation of 70 years of TB data enabled machine learning models to improve selection of small molecule, anti-tubercular compounds with in vivo activity. Using machine learning classification models (Bayesian, support vector machines, and recursive partitioning), Ekins et al. [31] first predicted eight new compounds that should be effective in treating TB. Extending their model to consider 60 additional small molecules with in vivo data, they were able to classify 41 of these as actives [30•]. Using a new data visualization approach called honeycomb visualizations, they then clustered the compounds and showed how the 60 new compounds are dispersed, providing a novel way for compound activity and potential to be assessed [30•].
As an important component of the total global burden, TB in children is a significant public health problem [5]. Using a mechanistic mathematical model of TB in children with drug resistance patterns, Dodd et al. [5] produced country-level, regional, and global estimates of drug-resistant infection and disease and estimated that 850,000 children developed TB in 2014. Importantly, their results suggested that there was a higher level of drug-resistant TB in children than had been diagnosed, which has redirected the focus of TB modeling to multidrug-resistant tuberculosis [32].
Antibiotic Resistance
Antibiotics remain the cornerstone of modern medicine; however, antibiotic resistance (ABR) presents a major issue for future generations [7]. It has long been known that antibiotics exert a selective pressure that results in resistant strains [33]. This Darwinian process has been the focus of numerous mathematical models of ABR and a variety of other diseases (e.g., cancer [34]). By considering interaction networks, modeling transmission of resistance has important consequences for controlling infectious disease spread [35, 36]. For example, from a dynamic transmission model tracking ABR acquisition in humans, Knight et al. [36] found that ABR is most likely community acquired rather than nosocomial, implying that antibiotic stewardship efforts should include the community.
ABR spread in hospitals, including healthcare-associated urinary tract infection (HAUTI), is another major concern associated with increased morbidity and mortality risks. Using Bayesian weighted incidence syndromic antibiogram (WISCA), Tandogdu et al. [37] compared HAUTI antibiotic coverage between urology departments in Europe and estimated that the chance a specific antibiotic provided coverage of causative pathogens when used as a first-line treatment was 63.4% for amoxicillin and 33.4% for imipenem (pooled overall incidence). Their analysis highlighted an 81% variation in the choice of antibiotics between HAUTI conditions (cystitis, pyelonephritis, and urosepsis), suggesting that personalized empirical antibiotic choices were needed based on causative pathogens and symptoms.
Multidrug antibiotic resistance (MDR) further presents a major issue in the treatment of TB. Applying statistical inference strategies (including a prior hypothesis and data-mining procedure) to a case-control study comparing drug resistance-associated mutations from Mycobacterium tuberculosis in households with transmission (Fig. 2b), Salvatore et al. [32] characterized fitness of different multidrug-resistant TB strains. They concluded that strains carrying the katG Ser315Thr mutation without the rpsL Lys43Arg substitution were associated with an increased probability of generating secondary cases.
Without new antibiotics, other treatment modalities have been sought to combat ABR. Encouragingly, antibacterial peptides, essential components of host defenses against microbial infections, have been shown to kill multidrug-resistant microorganisms, including bacteria [38]. To rationally design short, unnatural amino acids with potent antimicrobial activity, Wang et al. [38] combined computer-aided modeling, in vitro susceptibility tests, peptide characterization, and machine learning to develop statistical regression predictors to guide and improve the molecular design and structural optimization of unnatural antibacterial peptides. Overall, they demonstrated that ABPs with hybrid structure properties had the highest potency against three bacterial strains (Staphylococcus aureus, Pseudomonas aeruginosa, and Escherichia coli), motivating the use of in silico screens against ABR and other pathogens.
Parasites
Malaria
A number of within-host models describing the dynamics of malaria infection (Fig. 3) have been developed to predict outcomes with and without preventative measures and antimalarial drug treatment [4, 39, 40–41, 42••, 43]. By combining mechanistic model simulations with statistical learning, Georgiadou et al. [39] predicted that slower parasite growth and a longer duration of illness could distinguish severe anemia from cerebral malaria in infected individuals. They also found that the growth of Plasmodium falciparum is inhibited by cathepsin 9 and matrix metalloproteinase 9, suggesting potential therapeutic uses for these encoding proteins [39]. Using nonlinear models and individual-based models for malaria transmission, Hogan et al. [42••] simulated vaccine efficacy and antibody titers induced by B cell responses and found that the initial vaccine efficacy, duration, dosage, and timing of vaccination had different outcomes on the number of clinical cases averted [42••, 44, 45], which indicates that prioritizing initial efficacy over duration of protection may be advantageous for a childhood malaria vaccine with suboptimal efficacy. Further, their results suggest that a greater number of childhood clinical cases in areas of high malaria transmission could be prevented if initial vaccine efficacy was high rather than providing lengthy protection [42••].
Standard models for malaria. Khoury et al. [4] reviewed the main within-host models for malaria infections. (a) The Plasmodium falciparum life cycle begins with (A) infection in a host by an infectious mosquito. (B) Sporozoites traverse the bloodstream to the liver where they infect liver cells and replication and rupture to release merozoites into the blood. (C) Merozoites invade red blood cells (RBCs), and the parasite matures into schizont, which rupture RBCs to create more merozoites. (D) Some parasites commit to sexual development producing gametocytes (E), which are then taken up by mosquitos during a blood meal. (b) The standard ODE model of Plasmodium infection considers uninfected RBCs (U) and parasitized RBCs (P), which are created when a merozoite (M) infects an RBC. (c–d) Age-structured models are also used to model Plasmodium infection with either (c) an ODE system representing the stages of development of the parasitized RBC compartment or its equivalent partial differential equation formalism. Reprinted with permission from [4]
Within-host models of host-parasite interactions paired with pharmacokinetic and pharmacodynamic (PK/PD) models have also been used to predict the mechanisms of action and efficacy of various antimalarial therapies [43, 46,47,48]. In a recent clinical trial, modeling the effects of the novel antimalarial drug SJ733 predicted that this compound induces rapid parasite clearance and two-staged efficacy, with maximal results following recirculation of the drug [43]. PK analysis also found that the half-life of SJ733 is comparable with other fast-acting antimalarial drugs. The Guar et al. [43] model captured oscillatory parasite dynamics, suggesting distinct rates of parasite growth and clearance between individuals, and predicted that increased drug exposure could sustain parasitic decline, motivating the need for a follow-up study aiming to maximize exposure.
Examining malaria dynamics across biological scales has also elucidated important insights into the effects of antimalarial drugs, disease dynamics, and host immune control [49, 50]. For example, Cao et al. [51] linked gametocyte dynamics (sexual blood stage of Plasmodium, transmitted from human to the mosquito) with epidemiological dynamics to predict that human-to-mosquito transmissibility is influenced by the level of gametocytemia, which is altered by the sexual commitment rate and gametocyte sequestration time. Lönnberg et al. [52] used single-cell RNA sequencing and Gaussian process modeling to reveal a close molecular relationship between CD4+ T cell subsets in malaria infection and inflammatory macrophages in controlling the fate of differentiating CD4+ T cells. Lastly, Legros and Bonhoeffer [49] assessed the evolution of drug resistance by employing a multiscale, stochastic framework and found that treatment coverage has a stronger impact on disease prevalence and should therefore constitute the primary focus of disease control efforts over treatment efficacy, which was found to mainly affect the spread of resistance. Interestingly, this work suggested that the spread of resistance was generally less likely in areas of intense transmission [49].
Viruses
From intracellular viral replication to global disease pandemics, viral-borne infectious diseases have long been studied using mathematical modeling, focused especially on human immunodeficiency virus (HIV) and influenza infections (Fig. 4). This work is now being leveraged to study SARS-CoV-2. Modeling of the immune response to viruses has also helped to inform treatment of viral diseases [34, 53,54,55,56,57], and a recent study also considered viral-borne plant disease epidemics [58].
Viral modeling in HIV and influenza. (a) Hill et al. [73] described how an augmented viral dynamics model can be used to simulate antiretroviral therapy and the evolution of drug resistance in HIV. Uninfected cells (U) become infected (I) from infection by virus (V). Infected cells can become latently infected (L) and can be reactivated to produce actively infected cells. Latently infected cells are a crucial compartment to consider for long-term therapy outcomes as temporary administration of fully suppressive therapy can falsely be predicted to cure infection. Simulating an example of a drug taken daily with 70% probability, the impact on the viral load, and R0 for wild-type and resistant strains is significantly different over 20 days. Reprinted open access [73]. (b) Smith [91] summarized the major components of modeling viral infections, including innate and adaptive immune response (IR) dynamics. Viral dynamics are represented by an ODE viral kinetic model with an eclipse phase (I1) and an infected cell clearance which is a function of the infection cell population. Macrophages (M) play a major role in the innacte IR clearing up virus and also producing cytokines which block the production of new virions. In the adaptive immune response, T cells (E) play a major role in the clearance of infected cells with the addition of activated B cells (B) and antibody (A) production leading to eventual viral clearance. Viral load dynamics observed in actue and chronic infections can be significantly different depending on the underlying viral and IR kinetics. Reprinted from Current Opinion in Systems Biology, Volume 12, A.M. Smith, Validated Models of Immune Response to Virus Infection, Page 47, Copyright (2018), with permission from Elsevier
HIV
The field of viral dynamics modeling has been instrumental for understanding the emergence of HIV and the ensuing epidemic, particularly for understanding the evolution of host/virus interactions [59,60,61,62,63,64,65,66,67], predicting treatment responses [68,69,70], and designing novel and more effective therapeutic approaches [69, 71, 72•]. Both Hill et al. [73••] and Perelson [20] provide extensive reviews of viral dynamics in the context of HIV and in interaction with the immune system.
Similar to the basic epidemic infection model in Eqs. (1), (2), and (3), the classic within-host mathematical model of HIV infection is described by a population of uninfected CD4+ target cells T(t), infected cells I(t), and virus V(t) (Fig. 3a; see [73••] for a more detailed review). The model has been shown to capture dynamics of both acute and chronic infection [73••] and can be extended through quasispecies kinetics to capture the emergence of multiple drug-resistant strains [72•]. The ability to track multiple mutations is particularly relevant to treatment, as HIV replicates by error-prone mechanisms [74] and accommodates high levels of genetic diversity [75].
The advent of antiretroviral (ARV) drugs has been transformative in the effort to reduce the number of HIV-related deaths and yet has not fully controlled the epidemic. Treatment with ARV drugs can be viewed as an overwhelming success, but the need for the lifelong management of treated HIV infections brings about several complicating factors. Drug resistance may exist before treatment begins or evolve over the long course of therapy, and ARV drugs (triple combination of highly active antiretroviral therapy or HAART) must be taken daily, and the consequences of poor adherence can be severely detrimental to an individual’s health [76]. During therapy breaks, drug levels drop (Fig. 4a), and viral replication can rapidly restart. This leads to immunologic damage and to an increased chance of generating mutations that produce drug-resistant strains [68]. Ngina et al. [77] studied HIV drug resistance with a quasispecies model describing susceptible, wild-type (WT)-infected, mutant-infected latently WT-infected treated with a reverse transcriptase inhibitor (RTI), and mutant-infected RTI-treated cells in addition to WT and resistant virions, and non-activated and activated CD8+ T cells. Their interest was in applying control theory to understand effective treatment with an RTI and a protease inhibitor (PI) was accomplished by introducing control variables to represent each drug type and the degree of drug-resistant mutation. This approach allowed the authors to conclude that bang-bang control was critical to apply to the model, given that they found that PI control of the mutant population decreased much faster than that of RTIs.
Recent work in anti-HIV therapy has been focused on proactively addressing the problems of ARV adherence and drug resistance through developing alternatives to daily treatment regimens. Some pharmacology-focused groups are working towards extended- and sustained-release oral drug formulations [78, 79], while others have explored alternative routes of drug administration or delivery that allow for slower, controlled release of ARVs [80, 81]. Activation of the latent HIV reservoir has also been explored as a means of eradicating the virus from the body [82], something that is not feasible with current HAART.
Pre-exposure prophylaxis (PrEP) is currently available as a daily two-drug pill. Similar considerations with respect to adherence arise during PrEP; however, here poor adherence can lead to an increased risk of transmission due to lower drug concentrations in relevant tissues. Several long-acting and extended-release drug delivery methods have also been suggested for PrEP [83]. A novel method of addressing the need for long-term suppressive coverage that reduces an individual’s pill-taking burden is the long-acting, gastric-retentive drug delivery devices that sustainably deliver drugs over days and months [84]. To that end, Kirtane et al. [71•] developed a gastric-retentive device able to deliver ARV for 7 days after ingestion. To predict the impact on virologic suppression as compared with commercially available drug, the authors developed a quasispecies model of HIV infection dynamics during treatment with daily pills and the long-acting drug delivery system that also accounted for variable adherence and predicted that the novel, weekly long-acting device provided similar suppression of wild-type and mutant, drug-resistant strains, given a similar level of adherence. Further, they predicted that the maximal concentration of the long-acting delivery system could be reduced relative to daily ART while still maintaining viral suppression.
Despite positive developments in long-acting oral ARV formulations and other delivery methods, a major hurdle to effective HIV cure is the presence of latent reservoirs (Fig. 4a) and protected physiological sites that prevent eradication within the host [85]. Quantifying the size of the viral reservoir is thus critical to predicting infection dynamics, particularly for individuals experiencing treatment interruption during which viral loads rebound and resistant strains may be established. Combining experimental and modeling work, Wang et al. [86] identified the ability for CD4+ T cells infected with replication-competent virus to proliferate when T cell receptors were stimulated or when stimulated by IL-7 to proliferate. Interestingly, when these CD4+ T cells were clonally expanded, certain clones persisted while others waxed and waned. Their findings substantiate the idea that the maintenance of the latent reservoir is provided by clonal proliferation that must be balanced by infected cell loss in the latent reservoir. The eradication of the latent reservoir with vorinostat, a drug used to manage persistent cutaneous T cell lymphoma [87], has also been studied as a latency reversing agent (LRA) in HIV-positive individuals who are on combination ART [88]. In addition to activating HIV RNA, vorinostat also heterogeneously modulates host cell gene transcription. Understanding the variable individual response is critical to establishing safe therapeutic protocols that are durably effective. Ke et al. [82] constructed two models that incorporate the basic viral dynamic model with new equations for the latent reservoir where seeding occurs either directly from a pool of sustainably activated cells or a delayed compartment. The pharmacodynamics of ART and vorinostat were modeled by blocking infection of target cells (ART) or the activation of latently infected cells (vorinostat). Fitting to viral load data from individuals enrolled in a vorinostat clinical trial showed that the multistage latent activation model was better at describing early viral loads, suggesting that variability in the distribution across the multiple activation stages accounts for the heterogeneity in vorinostat responses.
For both the London and Berlin patients (two individuals who received allogeneic hematopoietic stem cell transplantations with cells that do not express the CCR5 receptor, which is required for HIV entry into cells), LRA strategies have proven fruitful. The successful design of ART interruption trials, where LRAs are administered and ART treatment is suspended, rests upon correctly quantifying the viral reservoir size and kinetics controlling rebound during ART cessation. Hill et al. [89] identified ideal scheduling strategies by modeling these dynamics with a fully stochastic HIV viral dynamics quasispecies model that accounts for productively infected CD4+ T cells that release viral particles upon bursting or die without burst. Their results predicted that sampling must occur at least every 2 weeks to reduce the viral rebound and reservoir reseeding after ART interruption. Hill et al. [89] also demonstrated how the criticality of consistent patient monitoring to catching viral rebounds by applying their model to cases of two patients in Boston who underwent hematopoietic stem cell transplantation and ART cessation. Both patients ultimately experienced viral load rebounds and required reintroduction of ART to achieve viral suppression. The authors further concluded that the integration of mechanistic modeling and Bayesian uncertainty analysis is a de facto requirement to design effective and safe clinical trials. Gupta et al. [90••] extended these analyses to study the London patient for durable HIV-1 cure. Viral loads from plasma, semen, cerebrospinal fluid, gut biopsy, lymph node tissue, and cells were quantified using ultrasensitive assays and qtPCR to measure HIV-1 RNA and DNA levels. A mathematical model was applied to estimate the distribution of time to viral rebound given the size of the latent reservoir and chimerism (target cell fraction) which, combined with the Bayesian inference framework established in Hill et al. [89], allowed for the estimation of the probability of the number of cells remaining in the reservoir, and the likelihood no rebound would be observed off ART over a given time. Excitingly, the model and sampling observations suggest that the London patient has achieved HIV-1 cure.
Influenza
Several mathematical models have been developed to quantify the contribution of different immune responses and how they regulate primary influenza virus infection and related viral and bacterial coinfection (Fig. 4b, detailed review in [91••, 92]). Close comparison to data and, in some cases, follow-up validation studies have led to robust hypothesis discrimination and verification of model-derived parameter estimates (reviewed in [105••]), including a strong likelihood that epitope masking by antibodies reduces B cell stimulation during subsequent influenza infections [93] and a substantial (85–90%) inhibition of resident macrophages over the course of influenza that facilitates bacterial complications [94, 95•]. A better understanding of the spatiotemporal dynamics and how initial deposition and transport of virus throughout the respiratory tract contribute to the infection have been the focus of recent studies [96,97,98,99]. The models highlighted a potential for extended viral shedding at the nasopharynx and the possibility for heterogeneous dynamics at the cellular and host levels. These differences together with divergent dynamics during multi-pathogen infections [94, 95•, 100,101,102] may have robust downstream consequences on influenza epidemiology [103].
Highly pathogenic viruses like SARS and H1N1 can significantly impact people’s lives causing severe health, social, and economic damages [9]. Recent outbreaks of these viruses stressed the urgency of effective research on the dynamics of infectious disease spread. Ming et al. [9] developed an empirically evaluated stochastic model that allowed the investigation of transmission patterns of infectious diseases in heterogeneous populations. They tested their model on surveillance data from 2009 H1N1 pandemic in Hong Kong and showed that it had a 20% mean absolute percentage error in terms of the forward predication. Moving into the future, modeling pandemics in this way could provide valuable insight for public health authorities to predict disease spread and guide control efforts [104] developed a system to detect infected patients by classification using vital signs, respiration rate, heart rate, and facial temperatures and determining those at higher risk for influenza using neural network and fuzzy clustering method.
SARS-CoV-2
Understanding the early transmission dynamics of SARS-CoV-2 infection and evaluating effective control measures is crucial for controlling spread and preventing undue death from coronavirus disease (COVID-19). To estimate these early dynamics, Kucharski et al. [6] combined a stochastic transmission model with data measuring new cases within and outside Wuhan, China, the original epicenter and found that the median effective reproduction number in Wuhan declined from 2.35 to 1.05 within 2 weeks of the introduction of travel restrictions, and a > 50% change of infection establishing in locations with similar transmission potential to Wuhan following introduction of four independent infections. To infer the proportion of early SARS-CoV-2 infections that went undetected and their contribution to the virus spread, Li et al. [17] used a network dynamic metapopulation model and Bayesian inference to estimate that ~ 86% of cases were undocumented before travel restrictions were implemented. As in other infectious diseases, it is crucial to understand the routes and timings of transmission to impose optimal isolation, physical distancing, decontamination, and hygiene measures. Flaxman et al. [105••] used a mathematical model originally developed for influenza to investigate the effects of non-pharmaceutical interventions on healthcare demand, soon after which multiple countries implemented more stringent distancing and stay-at-home measures. To this end, Ferretti et al. [106] developed a mathematical model where infectiousness varied as a function of time since infection, which suggested epidemic control by manual contact tracing was infeasible and that the use of a contact-tracing app with memory of contact proximity and notifications to contacts could aid effective containment.
A case study for the dynamics of the COVID-19 pandemic was the Diamond Princess cruise ship. After a patient tested positive on the 1st of February 2020, 3711 passengers and crew members were quarantined and tested extensively [107]. Adjusting for delay from confirmation to death, case and infection fatality ratios for COVID-19 on the Diamond Princess ship were estimated by Russell et al. [107] as 2.6% and 1.3%, respectively. Their analysis highlighted the importance of adjusting for delays from confirmation to outcome in real-time establishment of fatality risk for COVID-19 and provided early necessary insight into disease severity.
Characteristics of COVID-19 typically include a range of respiratory symptoms (e.g., fever and cough) [108]. In severe cases, symptoms progress to acute respiratory distress syndrome (ARDS) and are frequently accompanied by a variety of inflammatory indications [109], such as increased IL-6 and delayed type I IFN. A major challenge has been distinguishing risk factors for severe versus mild manifestations. To that aim, a large sweep of within-host viral dynamics models is currently being rapidly developed to understand SARS-CoV-2 dynamics and therapeutic efficacy all of which are still in the pre-print stage.
Conclusions and Future Perspectives
Innovative mathematical and computational modeling have led to significant advancements in preventing disease spread and improving treatment of infectious diseases. Modeling efforts have been deployed in close collaboration with experimentalists, clinicians, and public health specialists to provide a pathway towards rational and implementable studies at the bench, bedside, and policy levels. The global incidence of infectious diseases requires a comprehensive and interdisciplinary approach to achieve goals like the complete eradication of TB by 2050 and the 90-90-90 target (90% of all people living with HIV will know their HIV status; 90% of all people with diagnosed HIV infection will receive sustained antiretroviral therapy; 90% of all people receiving antiretroviral therapy will have viral suppression) for HIV treatment. This is epitomized by the modeling, scientific, and global community’s massive ongoing efforts to understand the SARS-CoV-2 virus and end the ongoing pandemic. The studies highlighted here have aided governance decisions that facilitate reduced fatality rates and disease spread and motivate fundamental biomedical investigations at multiple scales (e.g., intracellular, within-host, and between-host within contained communities or worldwide). Rapid real-time development of models for the systemic immune response has been seen throughout the world. Some of which use tissue-simulating agent-based models, and others use simple ODE systems calibrated to SARS-CoV-2 viral load measurements. While still in progress, this research is helping improve the understanding of COVID-19 and to predict distinguishing factors of severe and mild disease.
Given the historic contributions of mathematical and computational modeling to understanding the spread of infectious diseases and their effects within individuals, we expect that modeling will continue to play a major role in global disease response, treatment, and prevention.
References
Papers of particular interest, published recently, have been highlighted as: • Of importance •• Of major importance
Fenton A. Editorial: mathematical modelling of infectious diseases. Parasitology. 2016;143:801–4.
Siettos CI, Russo L. Mathematical modeling of infectious disease dynamics. Virulence. 2013;4:295–306.
• Davis CL, Wahid R, Toapanta FR, Simon JK, Sztein MB. A clinically parameterized mathematical model of Shigella immunity to inform vaccine design. PLoS One. 2018;13:e0189571 The authors build a mechanistic differential equation models of the gut immune response to Shigella in humans. Using Latin hypercube sampling and Monte Carlo simulations for parameter estimation they fit their model to human immune data from two Shigella vaccine trails and a rechallenge study. From their work, they concluded that antibody-based vaccines that target lipopolysaccharide or proteins on Shigella’s outer membrane are unlikely to sufficiently protect against severe disease, deploying sensitivity analysis to identify other possible targets for further study.
Khoury DS, Aogo R, Randriafanomezantsoa-Radohery G, McCaw JM, Simpson JA, McCarthy JS, et al. Within-host modeling of blood-stage malaria. Immunol Rev. 2018;285:168–93.
Dodd PJ, Sismanidis C, Seddon JA. Global burden of drug-resistant tuberculosis in children: a mathematical modelling study. Lancet Infect Dis. 2016;16:1193–201.
Kucharski AJ, Russell TW, Diamond C, Liu Y, Edmunds J, Funk S, et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis. 2020;20:553–8.
Knight GM, Davies NG, Colijn C, et al. Mathematical modelling for antibiotic resistance control policy: do we know enough? BMC Infect Dis. 2019;19:1–9.
Garira W. A primer on multiscale modelling of infectious disease systems. Infect Dis Model. 2018;3:176–91.
Ming RX, Liu JM, William WK, Wan X. Stochastic modelling of infectious diseases for heterogeneous populations. Infect Dis Poverty. 2016;5:1–11.
Chang SL, Piraveenan M, Pattison P, Prokopenko M. Game theoretic modelling of infectious disease dynamics and intervention methods: a review. J Biol Dyn. 2020;14:57–89.
El Jarroudi M, Karjoun H, Kouadio L, El Jarroudi M. Mathematical modelling of non-local spore dispersion of wind-borne pathogens causing fungal diseases. Appl Math Comput. 2020;376:125107.
Agrebi S, Larbi A. Use of artificial intelligence in infectious diseases. Artif Intell Precis Heal. 2020:415–38.
Roddam AW (2001) Mathematical epidemiology of infectious diseases: model building, analysis and interpretation: O Diekmann and JAP Heesterbeek, 2000, Chichester: John Wiley pp. 303,£39.95. ISBN 0-471-49241-8.
Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc london Ser A, Contain Pap a Math Phys character. 1927;115:700–21.
Andraud M, Hens N, Marais C, Beutels P. Dynamic epidemiological models for dengue transmission: a systematic review of structural approaches. PLoS One. 2012;7:e49085. https://doi.org/10.1371/journal.pone.0049085.
Mukhtar AYA, Munyakazi JB, Ouifki R, Clark AE. Modelling the effect of bednet coverage on malaria transmission in South Sudan. PLoS One. 2018;13:1–22.
Li R, Pei S, Chen B, Song Y, Zhang T, Yang W, Shaman J (2020) Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science (80- ) 368:489–493.
Eftimie R, Gillard JJ, Cantrell DA. Mathematical models for immunology: current state of the art and future research directions. Bull Math Biol. 2016;78:2091–134.
Germain RN, Meier-Schellersheim M, Nita-Lazar A, Fraser IDC. Systems biology in immunology: a computational modeling perspective. Annu Rev Immunol. 2011;29:527–85.
Perelson AS, Ribeiro RM. Introduction to modeling viral infections and immunity. Immunol Rev. 2018;285:5–8.
Opatowski L, Guillemot D, Boëlle P-Y, Temime L. Contribution of mathematical modeling to the fight against bacterial antibiotic resistance. Curr Opin Infect Dis. 2011;24:279–87.
He Y, Rappuoli R, De Groot AS, Chen RT. Emerging vaccine informatics. J Biomed Biotechnol. 2010;2010.
Pappalardo F, Flower D, Russo G, Pennisi M, Motta S. Computational modelling approaches to vaccinology. Pharmacol Res. 2015;92:40–5.
Levine MM, Kotloff KL, Barry EM, Pasetti MF, Sztein MB. Clinical trials of Shigella vaccines: two steps forward and one step back on a long, hard road. Nat Rev Microbiol. 2007;5:540–53.
Plotkin SA, Gilbert PB. Nomenclature for immune correlates of protection after vaccination. Clin Infect Dis. 2012;54:1615–7.
Arevalillo JM, Sztein MB, Kotloff KL, Levine MM, Simon JK. Identification of immune correlates of protection in Shigella infection by application of machine learning. J Biomed Inform. 2017;74:1–9.
Davis CL, Wahid R, Toapanta FR, Simon JK, Sztein MB, Levy D. Applying mathematical tools to accelerate vaccine development: modeling Shigella immune dynamics. PLoS One. 2013;8:e59465.
Houben RMGJ, Dodd PJ. The global burden of latent tuberculosis infection: a re-estimation using mathematical modelling. PLoS Med. 2016;13:1–13.
Uplekar M, Weil D, Lonnroth K, Jaramillo E, Lienhardt C, Dias HM, et al. WHO’s new end TB strategy. Lancet. 2015;385:1799–801.
• Ekins S, Perryman AL, Clark AM, Reynolds RC, Freundlich JS. Machine learning model analysis and data visualization with small molecules tested in a mouse model of Mycobacterium tuberculosis infection (2014–2015). J Chem Inf Model. 2016;56:1332–43 The authors identify candidate compounds to pursue in mouse in vivo efficacy models for the treatment or Mycobaterium tuberculosis. They do this through machine learning and Bayesian models of in vivo Mycobaterium tuberculosis data generated by different laboratories using various mouse models. They show, for the first time, that consensus models can be used to predict in vivo activity of different treatment compounds and develop a new clustering method for data visualisation.
Ekins S, Pottorf R, Reynolds RC, Williams AJ, Clark AM, Freundlich JS. Looking back to the future: predicting in vivo efficacy of small molecules versus Mycobacterium tuberculosis. J Chem Inf Model. 2014;54:1070–82.
Salvatore PP, Becerra MC, zur Wiesch P, Hinkley T, Kaur D, Sloutsky A, et al. Fitness costs of drug resistance mutations in multidrug-resistant Mycobacterium tuberculosis: a household-based case-control study. J Infect Dis. 2016;213:149–55.
Davies J, Davies D. Origins and evolution of antibiotic resistance. Microbiol Mol Biol Rev. 2010;74:417–33.
Craig M, Jenner AL, Namgung B, Lee LP, Goldman A (2020) Engineering in medicine to address the challenge of cancer drug resistance: from micro- and nanotechnologies to computational and mathematical modeling. Chem. Rev. Under review.
Van Bunnik BAD, Woolhouse MEJ. Modelling the impact of curtailing antibiotic usage in food animals on antibiotic resistance in humans. R Soc Open Sci. 2017;4:161067.
Knight GM, Costelloe C, Deeny SR, Moore LSP, Hopkins S, Johnson AP, et al. Quantifying where human acquisition of antibiotic resistance occurs: a mathematical modelling study. BMC Med. 2018;16:137.
Tandogdu Z, Koves B, Cai T, Cek M, Tenke P, Naber K, et al. Condition-specific surveillance in health care-associated urinary tract infections as a strategy to improve empirical antibiotic treatment: an epidemiological modelling study. World J Urol. 2020;38:27–34.
Wang Y, Yang YJ, Chen YN, Zhao HY, Zhang S. Computer-aided design, structural dynamics analysis, and in vitro susceptibility test of antibacterial peptides incorporating unnatural amino acids against microbial infections. Comput Methods Prog Biomed. 2016;134:215–23.
Georgiadou A, Lee HJ, Walther M, van Beek AE, Fitriani F, Wouters D, et al. Modelling pathogen load dynamics to elucidate mechanistic determinants of host--Plasmodium falciparum interactions. Nat Microbiol. 2019;4:1592–602.
Khoury DS, Cromer D, Akter J, Sebina I, Elliott T, Thomas BS, et al. Host-mediated impairment of parasite maturation during blood-stage Plasmodium infection. Proc Natl Acad Sci. 2017;114:7701–6.
Wale N, Jones MJ, Sim DG, Read AF, King AA. The contribution of host cell-directed vs. parasite-directed immunity to the disease and dynamics of malaria infections. Proc Natl Acad Sci. 2019;116:22386–92.
•• Hogan AB, Winskill P, Verity R, Griffin JT, Ghani AC. Modelling population-level impact to inform target product profiles for childhood malaria vaccines. BMC Med. 2018;16:1–11 The authors simulated the changing anti-circumsporozoite antibody titre following vaccination for Plasmodium falciparum malaria and related the antibody titre to vaccine efficacy. The model they developed pairs an individual-based model of human transmission process with a stochastic compartment for the mosquito biology. Their study predicted the most important characteristics of malaria vaccines and showed how vaccine properties translate to public health outcomes.
Gaur AH, McCarthy JS, Panetta JC, et al. Safety, tolerability, pharmacokinetics, and antimalarial efficacy of a novel Plasmodium falciparum ATP4 inhibitor SJ733: a first-in-human and induced blood-stage malaria phase 1a/b trial. Lancet Infect Dis. 2020;20:964–75.
Winskill P, Slater HC, Griffin JT, Ghani AC, Walker PGT. The US President’s malaria initiative, Plasmodium falciparum transmission and mortality: a modelling study. PLoS Med. 2017;14:e1002448.
White MT, Griffin JT, Churcher TS, Ferguson NM, Basáñez M-G, Ghani AC. Modelling the impact of vector control interventions on Anopheles gambiae population dynamics. Parasit Vectors. 2011;4:153.
Khoury DS, Cromer D, Elliott T, Soon MSF, Thomas BS, James KR, et al. Characterising the effect of antimalarial drugs on the maturation and clearance of murine blood-stage Plasmodium parasites in vivo. Int J Parasitol. 2017;47:913–22.
Aogo RA, Khoury DS, Cromer D, Elliott T, Akter J, Fogg LG, et al. Quantification of host-mediated parasite clearance during blood-stage Plasmodium infection and anti-malarial drug treatment in mice. Int J Parasitol. 2018;48:903–13.
Burgert L, Rottmann M, Wittlin S, Gobeau N, Krause A, Dingemanse J, et al. Ensemble modeling highlights importance of understanding parasite-host behavior in preclinical antimalarial drug development. Sci Rep. 2020;10:1–12.
Legros M, Bonhoeffer S. A combined within-host and between-hosts modelling framework for the evolution of resistance to antimalarial drugs. J R Soc Interface. 2016;13:20160148.
Bushman M, Antia R, Udhayakumar V, de Roode JC. Within-host competition can delay evolution of drug resistance in malaria. PLoS Biol. 2018;16:e2005712.
Cao P, Collins KA, Zaloumis S, Wattanakul T, Tarning J, Simpson JA, et al. Modeling the dynamics of Plasmodium falciparum gametocytes in humans during malaria infection. Elife. 2019;8:e49058.
Lönnberg T, Svensson V, James KR, Fernandez-Ruiz D, Sebina I, Montandon R, et al. Single-cell RNA-seq and computational analysis using temporal mixture modelling resolves Th1/Tfh fate bifurcation in malaria. Sci Immunol. 2017;2:eaal2192.
Jenner AL, Frascoli F, Yun C-O, Kim PS. Optimising hydrogel release profiles for viro-immunotherapy using oncolytic adenovirus expressing IL-12 and GM-CSF with immature dendritic cells. Appl Sci. 2020;10:2872.
Cardozo EF, Apetrei C, Pandrea I, Ribeiro RM. The dynamics of simian immunodeficiency virus after depletion of CD8+ cells. Immunol Rev. 2018;285:26–37.
Ciupe SM. Modeling the dynamics of hepatitis B infection, immunity, and drug therapy. Immunol Rev. 2018;285:38–54.
Best K, Perelson AS. Mathematical modeling of within-host Zika virus dynamics. Immunol Rev. 2018;285:81–96.
Schiffer JT, Swan DA, Prlic M, Lund JM. Herpes simplex virus-2 dynamics as a probe to measure the extremely rapid and spatially localized tissue-resident T-cell response. Immunol Rev. 2018;285:113–33.
Al F, Sagar B, Ezio A, Ray S. Modelling the effect of incubation and latent period in the dynamics of persistently transmitted vector-borne viral plant disease. Bull Math Biol. 2020;82:1–31.
Nowak MA, Anderson RM, McLean AR, Wolfs TF, Goudsmit J, May RM (1991) Antigenic diversity thresholds and the development of AIDS. Science (80- ) 254:963–969.
Wei X, Ghosh SK, Taylor ME, Johnson VA, Emini EA, Deutsch P, et al. Viral dynamics in human immunodeficiency virus type 1 infection. Nature. 1995;373:117–22.
Rosenbloom DIS, Hill AL, Laskey SB, Siliciano RF. Re-evaluating evolution in the HIV reservoir. Nature. 2017;551:E6–9.
Reeves DB, Duke ER, Wagner TA, Palmer SE, Spivak AM, Schiffer JT. A majority of HIV persistence during antiretroviral therapy is due to infected cell proliferation. Nat Commun. 2018;9:1–16.
Koelle K, Farrell AP, Brooke CB, Ke R (2019) Within-host infectious disease models accommodating cellular coinfection, with an application to influenza. Virus Evol 5:vez018.
Mittler JE, Sulzer B, Neumann AU, Perelson AS. Influence of delayed viral production on viral dynamics in {HIV}-1 infected patients. Math Biosci. 1998;152:143–63.
Smith AM, Ribeiro RM. Modeling the viral dynamics of influenza A virus infection. Crit Rev Immunol. 2010;30.
Smith AM, Perelson AS. Influenza A virus infection kinetics: quantitative data and models. Wiley Interdiscip Rev Syst Biol Med. 2011;3:429–45.
Smith AM, McCullers JA, Adler FR, Perelson AS, Nowak MA, Anderson RM, et al. Influenza A virus infection kinetics: quantitative data and models. Wiley Interdiscip Rev Syst Biol Med. 2011;3:429–45.
Rosenbloom DIS, Hill AL, Rabi SA, Siliciano RF, Nowak MA. Antiretroviral dynamics determines HIV evolution and predicts therapy outcome. Nat Med. 2012;18:1378–85.
Schiffer JT, Swan DA, Magaret A, Corey L, Wald A, Ossig J, et al. Mathematical modeling of herpes simplex virus-2 suppression with pritelivir predicts trial outcomes. Sci Transl Med. 2016;8:324ra15. https://doi.org/10.1126/scitranslmed.aad6654.
Hill AL, Rosenbloom DIS, Fu F, Nowak MA, Siliciano RF. Predicting the outcomes of treatment to eradicate the latent reservoir for HIV-1. Proc Natl Acad Sci. 2014;111:13475–80.
Schiffer JT, Swan DA, Magaret A, Schacker TW, Wald A, Corey L. Mathematical modeling predicts that increased HSV-2 shedding in HIV-1 infected persons is due to poor immunologic control in ganglia and genital mucosa. PLoS One. 2016;11:e0155124.
• Kirtane AR, Abouzid O, Minahan D, et al. Development of an oral once-weekly drug delivery system for HIV antiretroviral therapy. Nat Commun. 2018;9:2 The authors developed and analysed the efficacy of a long-acting enteral antiretroviral therapy. Their oral dosage was composed of distinct drug-polyer matrices which achieved week-long systemic drug levels in pigs. Simulating the patient viral dynamics using a quasispecies model of HIV infection they predicted that the novel therapeutic would significantly reduce therapeutic failures and could avert hundreds of thousands of new HIV cases.
•• Hill AL, Rosenbloom DIS, Nowak MA, Siliciano RF. Insight into treatment of HIV infection from viral dynamics models. Immunol Rev. 2018;285:9–25 In this comprehensive review, the authors summarise the contributions of viral dynamic modelling to understanding the pathophysiology of infection and to designing effective therapies. They discuss relevant and impactful modelling work for antiretroviral therapy, the evolution of drug resistance, latency-reversing agents and immunotherapy.
Bebenek K, Abbotts J, Roberts JD, Wilson SH, Kunkel TA. Specificity and mechanism of error-prone replication by human immunodeficiency virus-1 reverse transcriptase. J Biol Chem. 1989;264:16948–56.
Markham RB, Wang W-C, Weisstein AE, Wang Z, Munoz A, Templeton A, et al. Patterns of HIV-1 evolution in individuals with differing rates of CD4 T cell decline. Proc Natl Acad Sci. 1998;95:12568–73.
Simoni JM, Pearson CR, Pantalone DW, Marks G, Crepaz N. Efficacy of interventions in improving highly active antiretroviral therapy adherence and HIV-1 RNA viral load: a meta-analytic review of randomized controlled trials. J Acquir Immune Defic Syndr. 2006;43:S23–35.
Ngina P, Mbogo RW, Luboobi LS. HIV drug resistance: insights from mathematical modelling. Appl Math Model. 2019;75:141–61.
Mateo MG, del Gutierrez M. M, Vidal F, Domingo P. Stavudine extended release (once-daily, Bristol-Myers Squibb) for the treatment of HIV/AIDS. Expert Opin Pharmacother. 2013;14:1055–64.
Davis SS. Formulation strategies for absorption windows. Drug Discov Today. 2005;10:249–57.
Rajoli RKR, Back DJ, Rannard S, Meyers CLF, Flexner C, Owen A, et al. Physiologically based pharmacokinetic modelling to inform development of intramuscular long-acting nanoformulations for HIV. Clin Pharmacokinet. 2015;54:639–50.
Hoeben E, Borghys H, Looszova A, Bouche M-P, van Velsen F, Baert L, others (2010) Pharmacokinetics and disposition of rilpivirine (TMC278) nanosuspension as a long-acting injectable antiretroviral formulation. Antimicrob Agents Chemother 54:2042–2050.
Ke R, Lewin SR, Elliott JH, Perelson AS. Modeling the effects of vorinostat in vivo reveals both transient and delayed HIV transcriptional activation and minimal killing of latently infected cells. PLoS Pathog. 2015;11:e1005237.
Nelson AG, Zhang X, Ganapathi U, Szekely Z, Flexner CW, Owen A, et al. Drug delivery strategies and systems for HIV/AIDS pre-exposure prophylaxis and treatment. J Control Release. 2015;219:669–80.
Verma M, Vishwanath K, Eweje F, Roxhed N, Grant T, Castaneda M, et al. A gastric resident drug delivery system for prolonged gram-level dosing of tuberculosis treatment. Sci Transl Med. 2019;11:eaau6267.
Huang Y, Hoque MT, Jenabian M-A, Vyboh K, Whyte SK, Sheehan NL, et al. Antiretroviral drug transporters and metabolic enzymes in human testicular tissue: potential contribution to HIV-1 sanctuary site. J Antimicrob Chemother. 2016;71:1954–65.
Wang Z, Gurule EE, Brennan TP, Gerold JM, Kwon KJ, Hosmane NN, et al. Expanded cellular clones carrying replication-competent HIV-1 persist, wax, and wane. Proc Natl Acad Sci. 2018;115:E2575–84.
Banerjee NS, Moore DW, Broker TR, Chow LT. Vorinostat, a pan-HDAC inhibitor, abrogates productive HPV-18 DNA amplification. Proc Natl Acad Sci. 2018;115:E11138–47.
Sung JA, Sholtis K, Kirchherr J, Kuruc JD, Gay CL, Nordstrom JL, et al. Vorinostat renders the replication-competent latent reservoir of human immunodeficiency virus (HIV) vulnerable to clearance by CD8 T cells. EBioMedicine. 2017;23:52–8.
Hill AL, Rosenbloom DI, Goldstein E, Hanhauser E, Kuritzkes DR, Siliciano RF, et al. Real-time predictions of reservoir size and rebound time during antiretroviral therapy interruption trials for HIV. PLoS Pathog. 2016;12:e1005535.
•• Gupta RK, Peppa D, Hill AL, et al. Evidence for HIV-1 cure after CCR5$Δ$32/$Δ$32 allogeneic haemopoietic stem-cell transplantation 30 months post analytical treatment interruption: a case report. Lancet HIV. 2020; The authors applied a mathematical model to estimate the distribution of time to viral rebound for The London patient (participant 36 in the IciStem cohort) after allogeneic stem-cell transplantation. Using a previously established Bayesian inference framework combined with their mathematical model they estimated the probability of cell remaining in the HIV reservoir and determined the likelihood of no rebound. From their analysis they proposed that the London patient has achieved HIV-1 cure.
•• Smith AM. Validated models of immune response to virus infection. Curr Opin Syst Biol. 2018;12:46–52 In this review, the author highlights how kinetic models of host-pathogen influenza have been insightful and helped to improve biological understanding of the immune response to virus infections. The author discusses how models are validated experimental to improve their predictive capabilities.
Smith AM. Host-pathogen kinetics during influenza infection and coinfection: insights from predictive modeling. Immunol Rev. 2018;285:97–112.
Zarnitsyna VI, Lavine J, Ellebedy A, Ahmed R, Antia R. Multi-epitope models explain how pre-existing antibodies affect the generation of broadly protective responses to influenza. PLoS Pathog. 2016;12:e1005692.
Smith AM, Adler FR, Ribeiro RM, Gutenkunst RN, McAuley JL, McCullers JA, et al. Kinetics of coinfection with influenza A virus and Streptococcus pneumoniae. PLoS Pathog. 2013;9:e1003238.
• Smith AM, Smith AP. A critical, nonlinear threshold dictates bacterial invasion and initial kinetics during influenza. Sci Rep. 2016;6:1–11 The authors analyse a kinetic model for secondary bacterial infection after influenza. Using a system of ODEs for the interaction and validation with data, they uncover a nonlinear initial dose threshold that is dependent on the amount of virus-induced alveolar macrophage depletion. They find that bacteria decline for dose-alveolar macrophage depletion combinations below the threshol and increase above the threshold.
Whitman J, Dhanji A, Hayot F, Sealfon SC, Jayaprakash C. Spatio-temporal dynamics of host-virus competition: a model study of influenza A. J Theor Biol. 2020;484:110026.
Haghnegahdar A, Zhao J, Feng Y. Lung aerosol dynamics of airborne influenza A virus-laden droplets and the resultant immune system responses: an in silico study. J Aerosol Sci. 2019;134:34–55.
Feng Y, Zhao J, Kleinstreuer C, Wang Q, Wang J, Wu DH, et al. An in silico inter-subject variability study of extra-thoracic morphology effects on inhaled particle transport and deposition. J Aerosol Sci. 2018;123:185–207.
Quirouette C, Younis NP, Reddy MB, Beauchemin CAA. A mathematical model describing the localization and spread of influenza A virus infection within the human respiratory tract. PLoS Comput Biol. 2020;16:e1007705.
Goto H, Ihira H, Morishita K, Tsuchiya M, Ohta K, Yumine N, et al. Enhanced growth of influenza A virus by coinfection with human parainfluenza virus type 2. Med Microbiol Immunol. 2016;205:209–18.
Gonzalez AJ, Ijezie EC, Balemba OB, Miura TA. Attenuation of influenza A virus disease severity by viral coinfection in a mouse model. J Virol. 2018;92.
Chan KF, Carolan LA, Korenkov D, Druce J, McCaw J, Reading PC, et al. Investigating viral interference between influenza A virus and human respiratory syncytial virus in a ferret model of infection. J Infect Dis. 2018;218:406–17.
Nickbakhsh S, Mair C, Matthews L, Reeve R, Johnson PCD, Thorburn F, et al. Virus--virus interactions impact the population dynamics of influenza and the common cold. Proc Natl Acad Sci. 2019;116:27142–50.
Sun G, Matsui T, Hakozaki Y, Abe S. An infectious disease/fever screening radar system which stratifies higher-risk patients within ten seconds using a neural network and the fuzzy grouping method. J Inf Secur. 2015;70:230–6.
•• Flaxman S, Mishra S, Gandy A, et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. 2020:1–5. The authors use a Bayesian mechanistic model to study the effect of major interventions across 11 European countries during the COVID-19 pandemic. They estimate for the countries they consider that the interventions have been sufficient to achieve control of the epidemic (drive R_t below 1). In summary, their results show that lockdowns have had a large effect on reducing transmission.
Ferretti L, Wymant C, Kendall M, Zhao L, Nurtay A, Abeler-Dörner L, Parker M, Bonsall D, Fraser C (2020) Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science (80- ) 368:0–7.
Russell TW, Hellewell J, Jarvis CI, Van Zandvoort K, Abbott S, Ratnayake R, et al. Estimating the infection and case fatality ratio for coronavirus disease (COVID-19) using age-adjusted data from the outbreak on the Diamond Princess cruise ship, February 2020. Eurosurveillance. 2020;25:6–10.
Rothan HA, Byrareddy SN. The epidemiology and pathogenesis of coronavirus disease (COVID-19) outbreak. J Autoimmun. 2020;109:102433.
Mehta P, McAuley DF, Brown M, Sanchez E, Tattersall RS, Manson JJ. COVID-19: consider cytokine storm syndromes and immunosuppression. Lancet. 2020;395:1033–4.
Funding
ALJ was funded through an FRQS Postdoctoral Fellowship and Centre for Applied Mathematics in Biosciences and Medicine (CAMBAM). ALJ and MC were supported through NSERC Discovery Grant RGPIN-2018-04546. AMS and RAA received funding from NIH R01AI139088.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
Adrianne L. Jenner, Rosemary A. Aogo, Courtney L. Davis, Amber M. Smith, and Morgan Craig declare that they have no conflict of interest.
Human and Animal Rights and Informed Consent
This article does not contain any studies with human or animal subjects performed by any of the authors.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the Topical Collection on Current State of the Science of Disease Modeling
Rights and permissions
About this article
Cite this article
Jenner, A.L., Aogo, R.A., Davis, C.L. et al. Leveraging Computational Modeling to Understand Infectious Diseases. Curr Pathobiol Rep 8, 149–161 (2020). https://doi.org/10.1007/s40139-020-00213-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40139-020-00213-x