Skip to main content
SpringerLink
Log in

Modified wavelet method for solving multitype variable-order fractional partial differential equations generated from the modeling of phenomena

  • Original Research
  • Published:
Mathematical Sciences Aims and scope Submit manuscript

Abstract

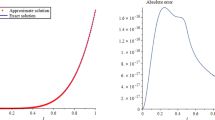
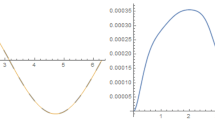
The aim of this paper is to introduce a new wavelet method for presenting approximate solutions of multitype variable-order (VO) fractional partial differential equations arising from the modeling of phenomena. In specific, this paper focuses on the numerical solution of the VO-fractional mobile-immobile advection-dispersion equation, Klein Gordon equation and Burgers equation. These equations are converted into a system of algebraic equations with the assistance of the bivariate Genocchi wavelet functions, their operational matrices, and the variable-order fractional Caputo derivative operator. Also, we present a new technique to get the operational matrix of integration and VO-fractional derivative. The modified operational matrices for solving the proposed equations are powerful and effective. So that, the accuracy of these matrices directly affects the implementation process. Finally, we consider numerical examples to confirm the superiority of the scheme, and for each example, exhibit the results through graphs and tables.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Sun, H.G., Chen, W., Wei, H., Chen, Y.Q.: A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur. Phys. J. Spec. Top. 193(1), 185 (2011)

    Article  Google Scholar 

  2. Shyu, J.J., Pei, S.C., Chan, C.H.: An iterative method for the design of variable fractional-order FIR differintegrators. Signal Process. 89(3), 320–327 (2009)

    Article  MATH  Google Scholar 

  3. Samko, S.G., Ross, B.: Integration and differentiation to a variable fractional order. Integr. Transform. Spec. Funct. 1(4), 277–300 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  4. Liu, F., Zhuang, P., Anh, V., Turner, I.: A fractional-order implicit difference approximation for the space-time fractional diffusion equation. ANZIAM. J. 47, 48–68 (2005)

    Article  MathSciNet  Google Scholar 

  5. Lorenzo, C.F., Hartley, T.T.: Variable order and distributed order fractional operators. Nonlinear Dyn. 29(1–4), 57–98 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  6. Lorenzo, C.F., Hartley, T.T.: Initialized fractional calculus. NASA Glenn Research Center (2000)

  7. Ramirez, L.E., Coimbra, C.F.: On the selection and meaning of variable order operators for dynamic modeling. Int. J. Differ. Equat. (2010). https://doi.org/10.1155/2010/846107

    Article  MathSciNet  MATH  Google Scholar 

  8. Ramirez, L.E., Coimbra, C.F.: A variable order constitutive relation for viscoelasticity. Annalen der, Physik. 16(7–8), 543–552 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  9. Zhuang, P., Liu, F., Anh, V., Turner, I.: Numerical methods for the variable-order fractional advection-diffusion equation with a nonlinear source term. SIAM. J. Numer. Anal. 47(3), 1760–1781 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hajipour, M., Jajarmi, A., Baleanu, D., Sun, H.: On an accurate discretization of a variable-order fractional reaction-diffusion equation. Commun. Nonlinear Sci. Numer. Simulat. 69, 119–133 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  11. Dehestani, H., Ordokhani, Y., Razzaghi, M.: Application of the modified operational matrices in multiterm variable-order time-fractional partial differential equations. Math. Meth. Appl. Sci. 42(18), 7296–7313 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  12. Lin, R., Liu, F., Anh, V., Turner, I.: Stability and convergence of a new explicit finite-difference approximation for the variable-order nonlinear fractional diffusion equation. Appl. Math. Comput. 212(2), 435–445 (2009)

    MathSciNet  MATH  Google Scholar 

  13. Doha, E.H., Abdelkawy, M.A., Amin, A.Z.M., Lopes, A.M.: A space-time spectral approximation for solving nonlinear variable-order fractional sine and Klein-Gordon differential equations. Comput. Appl. Math. 37(5), 6212–6229 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  14. Abd-Elkawy, M.A., Alqahtani, R.T.: Space-time spectral collocation algorithm for the variable-order Galilei invariant advection diffusion equations with a nonlinear source term. Math. Model. Anal. 22(1), 1–20 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  15. Nagy, A.M., Sweilam, N.H.: Numerical simulations for a variable order fractional cable equation. Acta. Math. Sci. 38(2), 580–590 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  16. Hassani, H., Naraghirad, E.: A new computational method based on optimization scheme for solving variable-order time fractional Burgers’ equation. Math. Comput. Simul. 162, 1–17 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  17. Jiang, W., Liu, N.: A numerical method for solving the time variable fractional order mobile-immobile advection-dispersion model. Appl. Numer. Math. 119, 18–32 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  18. Doha, E.H., Abdelkawy, M.A., Amin, A.Z.M., Baleanu, D.: Spectral technique for solving variable-order fractional Volterra integro-differential equations. Numer. Methods Partial Differ. Eq. 34(5), 1659–1677 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  19. Dehestani, H., Ordokhani, Y., Razzaghi, M.: On the applicability of Genocchi wavelet method for different kinds of fractional-order differential equations with delay. Numer. Linear. Algebra Appl. 26(5), e2259 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  20. Isah, A., Phang, C.: Genocchi Wavelet-like operational matrix and its application for solving non-linear fractional differential equations. Open Phys. 14(1), 463–472 (2016)

    Article  MATH  Google Scholar 

  21. Heydari, M.H., Hooshmandasl, M.R., Ghaini, F.M., Cattani, C.: Wavelets method for solving fractional optimal control problems. Appl. Math. Comput. 286, 139–154 (2016)

    MathSciNet  MATH  Google Scholar 

  22. Sahu, P.K., Ray, S.S.: Legendre wavelets operational method for the numerical solutions of nonlinear Volterra integro-differential equations system. Appl. Math. Comput. 256, 715–723 (2015)

    MathSciNet  MATH  Google Scholar 

  23. Yuttanan, B., Razzaghi, M.: Legendre wavelets approach for numerical solutions of distributed order fractional differential equations. Appl. Math. Model. 70, 350–364 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  24. Kajani, M.T., Ghasemi, M., Babolian, E.: Comparison between the homotopy perturbation method and the sine-cosine wavelet method for solving linear integro-differential equations. Comput. Math. Appl. 54(7–8), 1162–1168 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  25. Yuanlu, L.I.: Solving a nonlinear fractional differential equation using Chebyshev wavelets. Commun. Nonlinear. Sci. Numer. Simul. 15(9), 2284–2292 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  26. Heydari, M.H., Hooshmandasl, M.R., Mohammadi, F., Cattani, C.: Wavelets method for solving systems of nonlinear singular fractional Volterra integro-differential equations. Commun. Nonlinear Sci. Numer. Simul. 19(1), 37–48 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  27. Singh, R., Guleria, V., Singh, M.: Haar wavelet quasilinearization method for numerical solution of Emden-Fowler type equations. Math. Comput. Simul. 174, 123–133 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  28. Ma, H., Yang, Y.: Jacobi spectral collocation method for the time variable-order fractional mobile-immobile advection-dispersion solute transport model. E. Asian J. Appl. Math. 6(3), 337–352 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  29. Zhang, Y., Benson, D.A., Reeves, D.M.: Time and space nonlocalities underlying fractional-derivative models: Distinction and literature review of field applications. Adv. Water. Resour. 32, 561–581 (2009)

    Article  Google Scholar 

  30. Schumer, R., Benson, D.A., Meerschaert, M.M., Baeumer, B.: Fractal mobile/immobile solute transport. Water Resour. Res. 39, 1–12 (2003)

    Article  Google Scholar 

  31. Momani, S., Odibat, Z.M.: Fractional green function for linear time-fractional inhomogeneous partial differential equations in fluid mechanics. J. Appl. Math. Comput. 24(1–2), 167–178 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  32. Esen, A., Tasbozan, O.: Numerical solutions of time fractional Burgers equation. Acta Univ. Sapientiae Math. 7(2), 167–185 (2015)

    MathSciNet  MATH  Google Scholar 

  33. Akram, T., Abbas, M., Riaz, M.B., Ismail, A.I., Ali, N.M.: An efficient numerical technique for solving time fractional Burgers equation. Alex. Eng. J. 59(4), 2201–2220 (2020)

    Article  Google Scholar 

  34. Avazzadeh, Z., Hassani, H.: Transcendental Bernstein series for solving reaction-diffusion equations with nonlocal boundary conditions through the optimization technique. Numer. Methods. Partial. Differ. Equ. 35(6), 2258–2274 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  35. Dehestani, H., Ordokhani, Y., Razzaghi, M.: Fractional-order Legendre-Laguerre functions and their applications in fractional partial differential equations. Appl. Math. Comput. 336, 433–453 (2018)

    MathSciNet  MATH  Google Scholar 

  36. Canuto, C., Hussaini, M.Y., Quarteroni, A., Zang, T.A.: Spectral methods: fundamentals in single domains. Springer Science & Business Media (2007)

  37. Zhang, H., Liu, F., Phanikumar, M.S., Meerschaert, M.M.: A novel numerical method for the time variable fractional order mobile-immobile advection-dispersion model. Comput. Math. Appl. 66(5), 693–701 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  38. Sweilam, N.H., Al-Mekhlafi, S.M., Albalawi, A.O.: A novel variable-order fractional nonlinear Klein Gordon model: a numerical approach. Numer. Methods Partial Differ. Equ. 35(5), 1617–1629 (2019)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Elite Foundation and Alzahra University. We express our sincere thanks to the anonymous referees for valuable suggestions that improved the final manuscript.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Faculty of Mathematical Sciences, Alzahra University, Tehran, Iran

    Haniye Dehestani & Yadollah Ordokhani

  2. Department of Mathematics and Statistics, Mississippi State University, Starkville, MS, 39762, USA

    Mohsen Razzaghi

Authors
  1. Haniye Dehestani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yadollah Ordokhani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohsen Razzaghi
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed equally and significantly in writing this paper. Also, all authors read and approved the final manuscript.

Corresponding author

Correspondence to Yadollah Ordokhani.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dehestani, H., Ordokhani, Y. & Razzaghi, M. Modified wavelet method for solving multitype variable-order fractional partial differential equations generated from the modeling of phenomena. Math Sci 16, 343–359 (2022). https://doi.org/10.1007/s40096-021-00425-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40096-021-00425-1

Keywords

Mathematics Subject Classification

Search

Navigation