Skip to main content
SpringerLink
Log in

A compatible Hermite–Taylor matrix-collocation technique with convergence test for second-order partial integro-differential equations containing two independent variables with functional bounds

  • Original Research
  • Published:
Mathematical Sciences Aims and scope Submit manuscript

Abstract

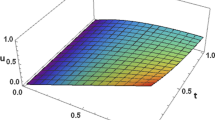
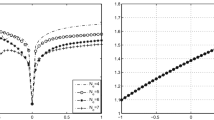
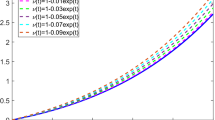
The aim of this study is to offer a compatible numerical technique to solve second-order linear partial integro-differential equations with variable (functional) bounds, including two independent variables, under the initial and/or boundary conditions by using hybrid Hermite and Taylor series. The method converts the presented integro-differential equation to a matrix equation including the unknown Hermite coefficients. Solving this matrix equation and applying the collocation method, the approximate solution of the problem is obtained in terms of the Hermite polynomials. Also, by means of an error estimation and convergence test related to residual functions, some examples to illustrate the accuracy and efficiency of the method are fulfilled; the obtained results are scrutinized and interpreted. All numerical computations have been performed on the computer programs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Abramowitz, M., Stegun, I.A., Miller, D.: Handbook of mathematical functions with formulas, graphs and mathematical tables (National Bureau of Standards Applied Mathematics Series No. 55). J. Appl. Mech. 32, 239 (1965)

    Google Scholar 

  2. Akgönüllü, N., Şahin, N., Sezer, M.: A hermite collocation method for the approximate solutions of high-order linear Fredholm integro-differential equations. Numer. Methods Partial Differ. Equ. 27(6), 1707–1721 (2011)

    MathSciNet  MATH  Google Scholar 

  3. Arfken, G.B., Weber, H.J.: Mathematical Methods for Physicists. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  4. Aslan, E., Kürkçü, Ö.K., Sezer, M.: A fast numerical method for fractional partial integro-differential equations with spatial-time delays. Appl. Numer. Math. 161, 525–539 (2020)

    MathSciNet  MATH  Google Scholar 

  5. Avazzadeh, Z., Heydari, M., Loghmani, G.: A comparison between solving two dimensional integral equations by the traditional collocation method and radial basis functions. Appl. Math. Sci. 5(23), 1145–1152 (2011)

    MathSciNet  MATH  Google Scholar 

  6. Avazzadeh, Z., Rizi, Z.B., Ghaini, F.M., Loghmani, G.: A numerical solution of nonlinear parabolic-type volterra partial integro-differential equations using radial basis functions. Eng. Anal. Bound. Elem. 36(5), 881–893 (2012)

    MathSciNet  MATH  Google Scholar 

  7. Aydin, T.A., Sezer, M.: Hermite polynomial approach to determine spherical curves in Euclidean 3-space. New Trends Math. Sci. 6(3), 189–199 (2018)

    Google Scholar 

  8. Behera, S., Ray, S.S.: An operational matrix based scheme for numerical solutions of nonlinear weakly singular partial integro-differential equations. Appl. Math. Comput. 367, 124771 (2020)

    MathSciNet  MATH  Google Scholar 

  9. Behzadi, S.S.: The use of iterative methods to solve two-dimensional nonlinear Volterra–Fredholm integro-differential equations. Commun. Numer. Anal. 2012, 1–20 (2012)

    MathSciNet  Google Scholar 

  10. Bülbül, B., Sezer, M.: Taylor polynomial solution of hyperbolic type partial differential equations with constant coefficients. Int. J. Comput. Math. 88(3), 533–544 (2011)

    MathSciNet  MATH  Google Scholar 

  11. Bülbül, B., Sezer, M.: A new approach to numerical solution of nonlinear Klein–Gordon equation. Math. Probl. Eng. 2013 (2013)

  12. Cayan, S., Sezer, M.: Pell polynomial approach for Dirichlet problem related to partial differential equations. J. Sci. Arts 19(3), 613–628 (2019)

    Google Scholar 

  13. Cayan, S., Sezer, M.: Lerch matrix collocation method for 2D and 3D Volterra type integral and second order partial integro differential equations together with an alternative error analysis and convergence criterion based on residual functions. Turk. J. Math. 44(6), 2073–2098 (2020)

    MathSciNet  Google Scholar 

  14. Darania, P., Shali, J.A., Ivaz, K.: New computational method for solving some 2-dimensional nonlinear Volterra integro-differential equations. Numer. Algorithms 57(1), 125–147 (2011)

    MathSciNet  MATH  Google Scholar 

  15. Dattoli, G.: Laguerre and generalized Hermite polynomials: the point of view of the operational method. Integral Transform. Spec. Funct. 15(2), 93–99 (2004)

    MathSciNet  MATH  Google Scholar 

  16. Dehghan, M.: Application of the adomian decomposition method for two-dimensional parabolic equation subject to nonstandard boundary specifications. Appl. Math. Comput. 157(2), 549–560 (2004)

    MathSciNet  MATH  Google Scholar 

  17. Fakhar-Izadi, F.: Fully spectral-Galerkin method for the one-and two-dimensional fourth-order time-fractional partial integro-differential equations with a weakly singular kernel. Numer. Methods Partial Differ. Equ. (2020). https://doi.org/10.1002/num.22634

    Article  Google Scholar 

  18. Fariborzi Araghi, M., Sadigh Behzadi, S.: Solving nonlinear Volterra-Fredholm integro-differential equations using he’s variational iteration method. Int. J. Comput. Math. 88(4), 829–838 (2011)

    MathSciNet  MATH  Google Scholar 

  19. Gökmen, E., Gürbüz, B., Sezer, M.: A numerical technique for solving functional integro-differential equations having variable bounds. Comput. Appl. Math. 37(5), 5609–5623 (2018)

    MathSciNet  MATH  Google Scholar 

  20. Guo, J., Xu, D., Qiu, W.: A finite difference scheme for the nonlinear time-fractional partial integro-differential equation. Math. Methods Appl. Sci. 43(6), 3392–3412 (2020)

    MathSciNet  MATH  Google Scholar 

  21. Guoqiang, H., Liqing, Z.: Asymptotic expansion for the trapezoidal nyström method of linear Volterra–Fredholm equations. J. Comput. Appl. Math. 51(3), 339–348 (1994)

    MathSciNet  MATH  Google Scholar 

  22. Gürbüz, B., Sezer, M.: A new computational method based on Laguerre polynomials for solving certain nonlinear partial integro differential equations. Acta Phys. Pol. A 132(3), 561–563 (2017)

    Google Scholar 

  23. Hadizadeh, M., Asgary, M.: An efficient numerical approximation for the linear class of mixed integral equations. Appl. Math. Comput. 167(2), 1090–1100 (2005)

    MathSciNet  MATH  Google Scholar 

  24. Hashim, H.E., Elzaki, T.M.: Solving singular partial integro-differential equations using Taylor series. Int. J. Innov. Sci. Eng. Technol. 2(1), 501–506 (2015)

    Google Scholar 

  25. Hendi, F., Al-Qarni, M.: The variational adomian decomposition method for solving nonlinear two-dimensional Volterra–Fredholm integro-differential equation. J. King Saud Univ. Sci. 31(1), 110–113 (2019)

    Google Scholar 

  26. Kürkçü, Ö.K., Aslan, E., Sezer, M.: A novel collocation method based on residual error analysis for solving integro-differential equations using hybrid Dickson and Taylor polynomials. Sains Malays 46, 335–347 (2017)

    MATH  Google Scholar 

  27. Kürkçü, Ö.K., Aslan, E., Sezer, M.: An advanced method with convergence analysis for solving space-time fractional partial differential equations with multi delays. Eur. Phys. J. Plus 134(8), 393 (2019)

    Google Scholar 

  28. Kurkcu, O.K., Aslan, E., Sezer, M.: A novel hybrid method for solving combined functional neutral differential equations with several delays and investigation of convergence rate via residual function. Comput. Methods Differ. Equ. 7(3), 396–417 (2019)

    MathSciNet  MATH  Google Scholar 

  29. Kürkçü, Ö.K., Sezer, M.: A directly convergent numerical method based on orthoexponential polynomials for solving integro-differential-delay equations with variable coefficients and infinite boundary on half-line. J. Comput. Appl. Math. 386, 113250 (2021)

    MathSciNet  MATH  Google Scholar 

  30. Lamiri, I,A,O.: d-orthogonality of Hermite type polynomials. Appl. Math. Comput. 202, 24–43 (2008)

    MathSciNet  MATH  Google Scholar 

  31. Loh, J.R., Phang, C., Tay, K.G.: New method for solving fractional partial integro-differential equations by combination of Laplace transform and resolvent kernel method. Chin. J. Phys. 67, 666–680 (2020)

    MathSciNet  Google Scholar 

  32. Mahgob, M.M.A., Elzaki, T.M.: Solution of partial integro-differential equations by Elzaki transform method. Appl. Math. Sci. 9, 295–303 (2015)

    Google Scholar 

  33. Mirzaee, F., Alipour, S., Samadyar, N.: A numerical approach for solving weakly singular partial integro-differential equations via two-dimensional-orthonormal Bernstein polynomials with the convergence analysis. Numer. Methods Partial Differ. Equ. 35(2), 615–637 (2019)

    MathSciNet  MATH  Google Scholar 

  34. Oldham, K.B., Myland, J., Spanier, J.: An Atlas of Functions: With Equator, the Atlas Function Calculator. Springer, Berlin (2010)

    MATH  Google Scholar 

  35. Ozel, M., Kurkcu, O.K., Sezer, M.: Morgan-Voyce matrix method for generalized functional integro-differential equations of Volterra-type. J. Sci. Arts 19(2), 295–310 (2019)

    Google Scholar 

  36. Poorfattah, E., Jafari Shaerlar, A.: Direct method for solving nonlinear two-dimensional Volterra–Fredholm integro-differential equations by block-pulse functions. Int. J. Inf. Secur. Syst. Manag. 4(1), 418–423 (2015)

    Google Scholar 

  37. Rahman, A., Fatt, F.: Adomian decomposition method for two-dimensional nonlinear Volterra integral equations of the second kind. Far East J. Appl. Math. 34, 167–179 (2009)

    MathSciNet  MATH  Google Scholar 

  38. Rainville, E.D.: Special Functions. Macmillan, New York (1960)

    MATH  Google Scholar 

  39. Rivaz, A., Yousefi, F., et al.: Two-dimensional Chebyshev polynomials for solving two-dimensional integro-differential equations. Çankaya Üniversitesi Bilim ve Mühendislik Dergisi 12(2), 1–11 (2015)

    Google Scholar 

  40. Rostami, Y.: Operational matrix of two dimensional Chebyshev wavelets and its applications in solving nonlinear partial integro-differential equations. Eng. Comput. 38(2), 745–761 (2021)

    Google Scholar 

  41. Sansone, G.: Orthogonal Functions, vol. 9. Courier Corporation, North Chelmsford (1959)

    MATH  Google Scholar 

  42. Singh, S., Patel, V.K., Singh, V.K.: Operational matrix approach for the solution of partial integro-differential equation. Appl. Math. Comput. 283, 195–207 (2016)

    MathSciNet  MATH  Google Scholar 

  43. Szegö, G.: Orthogonal Polynomials, p. 8724. AMS, Providence (1975)

    Google Scholar 

  44. Tari, A.: Modified homotopy perturbation method for solving two-dimensional Fredholm integral equations. Int. J. Comput. Appl. Math. 5(5), 585–593 (2010)

    MathSciNet  Google Scholar 

  45. Tari, A., Rahimi, M., Shahmorad, S., Talati, F.: Development of the tau method for the numerical solution of two-dimensional linear Volterra integro-differential equations. Comput. Methods Appl. Math. 9(4), 421–435 (2009)

    MathSciNet  MATH  Google Scholar 

  46. Thorwe, J., Bhalekar, S.: Solving partial integro-differential equations using Laplace transform method. Am. J. Comput. Appl. Math. 2(3), 101–104 (2012)

    Google Scholar 

  47. Weber, H.J., Arfken, G.B.: Essential Mathematical Methods for Physicists. Elsevier, Amsterdam (2003)

    MATH  Google Scholar 

  48. Yalçın, E., Kürkçü, Ö.K., Sezer, M.: A matched Hermite–Taylor matrix method to solve the combined partial integro-differential equations having nonlinearity and delay terms. Comput. Appl. Math. 39(4), 1–16 (2020)

    MathSciNet  MATH  Google Scholar 

  49. Yalçinbaş, S., Aynigül, M., Sezer, M.: A collocation method using Hermite polynomials for approximate solution of pantograph equations. J. Frankl. Inst. 348(6), 1128–1139 (2011)

    MathSciNet  MATH  Google Scholar 

  50. Yıldız, G., Tınaztepe, G., Sezer, M.: Bell polynomial approach for the solutions of Fredholm integrodifferential equations with variable coefficients. Comput. Model. Eng. Sci. 123(3), 973–993 (2020)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Manisa Celal Bayar University, Manisa, Turkey

    Elif Yalçın & Mehmet Sezer

Authors
  1. Elif Yalçın
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mehmet Sezer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Elif Yalçın.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yalçın, E., Sezer, M. A compatible Hermite–Taylor matrix-collocation technique with convergence test for second-order partial integro-differential equations containing two independent variables with functional bounds. Math Sci 16, 59–69 (2022). https://doi.org/10.1007/s40096-021-00393-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40096-021-00393-6

Keywords

Search

Navigation