Skip to main content
SpringerLink
Log in

Solution of singularly perturbed differential difference equations and convection delayed dominated diffusion equations using Haar wavelet

  • Original Reseatch
  • Published:
Mathematical Sciences Aims and scope Submit manuscript

Abstract

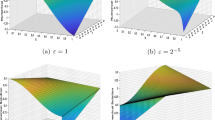
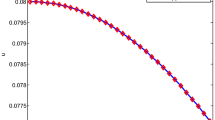
In this paper, we apply Haar wavelet collocation method to solve the linear and nonlinear second-order singularly perturbed differential difference equations and singularly perturbed convection delayed dominated diffusion equations, arising in various modeling of chemical processes. First, we transform delay term by using Taylor expansion and then apply Haar wavelet method. To show the robustness, accuracy and efficiency of the method, three problems of second-order singularly perturbed differential difference equations and three problems of convection delayed dominated diffusion equations have been solved. Also, results are compared with the exact solution of the problems and methods existing in the literature, which confirms the superiority of the Haar wavelet collocation method. We obtained accurate numerical solution of problems by increasing the level of resolutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Ahmad, K., Shah, F.A.: Introduction to Wavelets with Applications. Real World Education Publishers, New Delhi (2013)

    Google Scholar 

  2. Amiraliyev, G.M., Cimen, E.: Numerical method for a singularly perturbed convection–diffusion problem with delay. Appl. Math. Comput. 216, 2351–2359 (2010)

    MathSciNet  MATH  Google Scholar 

  3. Andargie, A., Reddy, Y.N.: An exponentially fitted special second-order finite difference method for solving singular perturbation problems. Appl. Math. Comput. 190, 1767–1782 (2007)

    MathSciNet  MATH  Google Scholar 

  4. Andargie, A., Reddy, Y.N.: Fitted fourth-order tridiagonal finite difference method for singular perturbation problems. Appl. Math. Comput. 192, 90–100 (2007)

    MathSciNet  MATH  Google Scholar 

  5. Aziz, T., Khan, A.: A spline method for second-order singularly perturbed boundary-value problems. J. Comput. Appl. Math. 147, 445–452 (2002)

    MathSciNet  MATH  Google Scholar 

  6. Bestehorn, M., Grigirieva, E.V.: Formation and propagation of localized states in extended systems. Ann. Phys. 13, 423–431 (2004)

    MathSciNet  MATH  Google Scholar 

  7. Brown, A.J.: Enzyme action. J. Chem. Soc. 81, 373–388 (1902)

    Google Scholar 

  8. Chen, C.F., Hsiao, C.H.: Haar wavelet method for solving lumped and distributed-parameter system. IEEE Proc. Control Theory Appl. 144, 87–94 (1997)

    MATH  Google Scholar 

  9. Challa, L.S., Reddy, Y.N.: Numerical integration of singularly perturbed delay differential equations using exponential integrating factor. Math. Commun. 22, 251–264 (2017)

    MathSciNet  MATH  Google Scholar 

  10. Chawla, M.M.: A fourth-order tridiagonal finite difference method for general non-linear two-point boundary value problems with mixed boundary conditions. J. Inst. Math. Appl. 21, 83–93 (1978)

    MathSciNet  MATH  Google Scholar 

  11. Chawla, M.M.: An efficient finite difference method for two-point boundary value problems. Neural Parallel Sci. Comput. 4, 384–396 (1996)

    MathSciNet  Google Scholar 

  12. Daubechies, I.: Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 41(7), 909–996 (1988)

    MathSciNet  MATH  Google Scholar 

  13. Debnath, L., Shah, F.A.: Wavelet Transform and Their Applications, pp. 337–440. Springer, New York (2015)

    Google Scholar 

  14. Frazier, M., Jawerth, B., Weiss, G.: Littlewood–Paley theory and the study of function spaces. In: CBMS Regional Conference Series in Mathematics. The American Mathematical Society, Providence, RI,  79 (1991)

  15. Grossmann, A., Morlet, J.: Decomposition of Hardy functions into square integrable wavelets of constant shape. SIAM J. Math. Anal. 15(4), 723–736 (1984)

    MathSciNet  MATH  Google Scholar 

  16. Geng, F.Z., Qian, S.P.: Improved reproducing kernel method for singularly perturbed differential–difference equations with boundary layer behavior. Appl. Math. Comput. 252, 58–63 (2015)

    MathSciNet  MATH  Google Scholar 

  17. Haar, A.: Zur theorie der orthogonalen funktionen-systeme. Math. Ann. 69, 331–371 (1910)

    MathSciNet  MATH  Google Scholar 

  18. Haidar, A., Legault, L., Dallaire, M., Alkhateeb, A., Coriati, A., Messier, V., Cheng, P., Millette, M., Boulet, B., Rabasa-Lhoret, R.: Glucose-responsive insulin and glucagon delivery (dual-hormone artiicial pancreas) in adults with type 1 diabetes: a randomized crossover controlled trial. CMAJ 5, 185 (2013)

    Google Scholar 

  19. Hernández, E., Weiss, G.: A First Course on Wavelets. Studies in Advanced Mathematics. CRC Press, Boca Raton (1996)

    MATH  Google Scholar 

  20. Islam, S., Aziz, I., Sarler, B.: The numerical solution of second order boundary value problems by collocation method with Haar wavelets. Math. Comput. Model. 50, 1577–90 (2010)

    MathSciNet  MATH  Google Scholar 

  21. Kadalbajoo, M.K., Sharma, K.K.: A numerical method based on finite difference for boundary value problems for singularly perturbed delay differential equation. Appl. Math. Comput. 197, 692–707 (2008)

    MathSciNet  MATH  Google Scholar 

  22. Kadalbajoo, M.K., Ramesh, V.P.: Hybrid method for numerical solution of singularly perturbed delay differential equations. Appl. Math. Comput. 187, 797–814 (2007)

    MathSciNet  MATH  Google Scholar 

  23. Kadalbajoo, M.K., Sharma, K.K.: A numerical analysis of singularly perturbed delay differential equations with layer behavior. Appl. Math. Comput. 157, 11–28 (2004)

    MathSciNet  MATH  Google Scholar 

  24. Kadalbajoo, M.K., Patidar, K.C., Sharma, K.K.: Uniformly convergent fitted methods for the numerical solution of the problems arising from singularly perturbed general DDEs. Appl. Math. Comput. 182, 119–139 (2006)

    MathSciNet  MATH  Google Scholar 

  25. Kadalbajoo, M.K., Kumar, D.: Fitted mesh B-spline collocation method for singularly perturbed differential–difference equations with small delay. Appl. Math. Comput. 204, 90–98 (2008)

    MathSciNet  MATH  Google Scholar 

  26. Khan, A., Khandelwal, P.: Non-polynomial sextic spline solution of singularly perturbed boundary-value problems. Int. J. Comput. Math. 91, 1122–1135 (2014)

    MathSciNet  MATH  Google Scholar 

  27. Khan, A., Khan, I., Aziz, T.: Sextic spline solution of singularly perturbed boundary-value problems. Appl. Math. Comput. 181, 432–439 (2006)

    MathSciNet  MATH  Google Scholar 

  28. Keenan, D.B., Mastrototaro, J.J., Voskanyan, G., Steil, G.M.: Delays in minimally invasive continuous glucose monitoring devices: a review of current technology. J. Diabetes Sci. Technol. 3, 1207–1214 (2009)

    Google Scholar 

  29. Kevorkian, J., Cole, J.D.: Perturbation Methods in Applied Mathematics, vol. 20, pp. 33–53. Springer, New York (1981)

    MATH  Google Scholar 

  30. Kumar, D., Kadalbajoo, M.K.: A parameter-uniform numerical method for time-dependent singularly perturbed differential–difference equations. Appl. Math. Model. 35, 2805–2819 (2011)

    MathSciNet  MATH  Google Scholar 

  31. Kumar, D., Kadalbajoo, M.K.: Numerical treatment of singularly perturbed delay differential equations using B-spline collocation method on Shishkin mesh. J. Numer. Anal. Ind. Appl. Math. 7, 73–90 (2012)

    MathSciNet  MATH  Google Scholar 

  32. Kumar, D., Kadalbajoo, M.K.: Numerical approximations for singularly perturbed differential–difference BVPs with layer and oscillatory behaviour. J. Numer. Math. 20, 33–53 (2012)

    MathSciNet  MATH  Google Scholar 

  33. Lange, C.G., Miura, R.M.: Singular perturbation analysis of boundary-value problems for differential–difference equations. v. small shifts with layer behavior. SIAM J. Appl. Math. 54, 249–272 (1994)

    MathSciNet  MATH  Google Scholar 

  34. Lepik, U.: Application of Haar wavelet transform to solving integral and differential equations. Appl. Math. Comput. 57(1), 28–46 (2007)

    MathSciNet  MATH  Google Scholar 

  35. Lepik, U.: Haar wavelet method for solving stiff differential equations. Math. Model. Anal. 14(4), 467–481 (2009)

    MathSciNet  MATH  Google Scholar 

  36. Lepik, U., Hein, H.: Haar Wavelet with Applications, pp. 7–44. Springer, Berlin (2014)

    MATH  Google Scholar 

  37. Mallat, S.G.: Multiresolution approximations and wavelet orthonormal bases of \(L^2({\mathbb{R}})\). Trans. Am. Math. Soc. 315(1), 69–87 (1989)

    MATH  Google Scholar 

  38. Nayfeh, A.H.: Perturbation Methods. Wiley, New York (1979)

    Google Scholar 

  39. Pandit, S., Kumar, M.: Haar wavelet approach for numerical solution of two parameters singularly perturbed boundary value problems. Appl. Math. Inf. Sci. 8(6), 2965–2974 (2014)

    MathSciNet  Google Scholar 

  40. Raza, A., Khan, A.: Haar wavelet series solution for solving neutral delay differential equations. J. King Saud Univ. Sci. 31, 1070–1076 (2019)

    Google Scholar 

  41. Raza, A., Khan, A.: Non-uniform Haar wavelet method for solving singularly perturbed differential difference equations of neuronal variability. Appl. Appl. Math. Int. J. (AAM) 6, 56–70 (2020)

    MathSciNet  MATH  Google Scholar 

  42. Shah, F.A., Abass, R., Iqbal, J.: Numerical solution of singularly perturbed problems using Haar wavelet collocation method. Cogent Math. 3, 1202504 (2016)

    MathSciNet  MATH  Google Scholar 

  43. Sharma, M., Kaushik, A., Chenglin, L.: Analytic approximation to delayed convection dominated systems through transforms. J. Math. Chem. 52, 2459–2474 (2014). https://doi.org/10.1007/s10910-014-0394-1

    Article  MathSciNet  MATH  Google Scholar 

  44. Schell, M., Ross, J.J.: Effects of time-delay in rate-processes. Chem. Phys. 85, 6489–6503 (1986)

    MathSciNet  Google Scholar 

  45. Saaty, T.L.: Modern Nonlinear Equations. Dover, New York (1981)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Jamia Millia Islamia, New Delhi, 110025, India

    Akmal Raza & Arshad Khan

  2. Department of Mathematics, Zakir Husain Delhi College, University of Delhi, New Delhi, Delhi, 110002, India

    Pankaj Sharma

  3. Department of Mathematics, Al-Falah University, Faridabad, 121004, India

    Khalil Ahmad

Authors
  1. Akmal Raza
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Arshad Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Pankaj Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Khalil Ahmad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Akmal Raza.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Raza, A., Khan, A., Sharma, P. et al. Solution of singularly perturbed differential difference equations and convection delayed dominated diffusion equations using Haar wavelet. Math Sci 15, 123–136 (2021). https://doi.org/10.1007/s40096-020-00355-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40096-020-00355-4

Keywords

Mathematics Subject Classification

Search

Navigation