Abstract
In this study, a numerical approach of the spectral collocation method coupled with a regularization technique is applied for solving an inverse parabolic problem of the heat equation in a quarter plane. The problem includes the estimation of an unknown boundary condition from an overspecified condition. The stable solution of the problem exists and is proved by Tikhonov regularization technique. The algorithm works without any mesh points or elements, and accurate results can be obtained efficiently. By employing the numerical algorithm on the problem, the resultant matrix equation is ill-condition. To regularize this matrix equation, we apply regularization technique, with the L-curve and general cross-validation criteria for choosing the regularization parameter. For demonstrating the performance and ability of the proposed algorithm, a test example is presented. The numerical results showed that the solution obtained with the algorithm designed in this paper is stable with the noisy data and the unknown boundary condition was recovered very well.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Inverse problems of partial differential equations have many applications in different sciences, e.g., physics, engineering, geoscience, finance, etc. In the last decades, the scientific research has begun to focus on inverse problems of heat conduction equation, e.g., for more details, see [1,2,3,4,5,6,7].
The heat conduction problems include two categories: direct and inverse problems. The direct problems are related to the determination of unknown temperature distribution at the domain in the presence of the known initial and boundary conditions and other physical properties. The inverse problems consist of not only determination of temperature distribution, but also an estimation of the diffusion coefficient or temperature/heat flux on the surface or other unknown parameters from the extra condition which is given usually by temperature measurements taken within the body.
The major difficulty of IHCPs is their instability, that is, the small error in input data causes the large change in output data according to Hadamard definition [1,2,3].
Due to the instability of the inverse problem, the computational treatment of such problems needs applying more accurate numerical methods to obtain a stable approximate solution. In recent years, IHCPs have been investigated from the analytical and numerical point of view, in the literature, e.g., [3,4,5,6, 8,9,10].
Some more relevant works are published regarding the estimation of boundary condition and heat flux in [9, 11,12,13,14].
We present in this paper a numerical algorithm based on collocation method for an IHCP, which does not require domain discretization. The solution is constructed from the linear combination of basis functions which are chosen in an appropriate way.
By using the solution of the direct problem, a numerical approach based on the collocation method is introduced. An ill-conditioned system is derived from discretization. The condition number of the resultant matrix increases with respect to the number of collocation points, and so by using standard algorithms, we cannot achieve good accuracy. Some kind of regularization is necessary for finding a stable solution.
The outline of this paper is organized as follows:
In Sect. 2, a mathematical model of our interest problem is introduced. In Sect. 3, the Tikhonov regularization method is applied to construct a stable solution of the ill-posed integral equation. Section 4 contains a numerical procedure based on the collocation method for solving the inverse problem. In Sect. 5, the regularization method for discrete ill-posed problem is applied to find a stable solution and introduced GCV and L-curve criteria for determining regularization parameter. In Sect. 6, a test problem is considered to investigate the validity and efficiency of the method. Section 7 contains the conclusions.
Problem formulation
Here, we consider an inverse problem of the heat conduction in a quarter plane and the unknown boundary condition has to be determined from temperature measurements at a fixed point of the domain. Consider the following problem:
where \(T\) represents the final time and \(f(x)\) and \(g(t)\) are piecewise known continuous functions in direct problem and M is a positive constant.
The inverse problem consists of determining \(u\left({x,t} \right)\) and boundary condition \(g(t)\) subject to the condition (2.2), and overspecified condition \(p(t)\), which is given by
This IHCP is ill-posed.
For the forward problem (2.1)–(2.4), the unique solution is given by [15],
By setting x = 1 and using (2.5), we obtain
When we set \(f\left( x \right) = 0\), Eq. (2.7) has the form
Equation (2.7) can be rewritten in terms of an integral operator equation as follows:
where the operator \(A\) for \(0 < t < T\) is defined by
and
and the operator \(A\) is represented by
The above first-kind integral Eq. (2.8) cannot be reduced into an integral equation of the second kind by differentiation, and so the problem is ill-posed. We can uniquely determine \(g\left( t \right)\) subject to \(G\left( t \right)\) belong to the range of \(A^{ - 1}\). Since the \(A^{ - 1}\) is unbounded, the noisy data of \(p\left( t \right)\) lead to large errors in \(g\left( t \right)\). In the next section, we show the existence stable solution of the operator integral Eq. (2.9) by Tikhonov regularization technique in continuous form.
The regularization method for ill-posed integral equation
It this section, a popular regularization method is applied for solving an ill-posed integral equation of the form (2.9). Since in practical applications, the input data \(p\left( t \right)\) are affected by noise, we apply Tikhonov regularization technique to an approximate solution in a stable way. Based on the main idea of the Tikhonov regularization approach, by introducing the smoothing functional \(M^{\lambda } \left[ {g,G} \right]\) which is called Tikhonov functional and stabilizing functional \(\Omega \left( g \right)\), an ill-posed problem is replaced by the following problem:
where \(\lambda\) is the regularization parameter and \(\Omega \left( g \right)\) is a stabilizer of the first-order constant coefficient which is defined on a Sobolev space \(W_{2}^{1}\) as:
The regularized solution \(g_{\lambda }\) for Eq. (2.9) is constructed by using the following minimization problem, which is stated by the following theorem:
Theorem 1
For every function\(G \in L_{2} \left[ {0,T} \right]\)and any positive\(\lambda ,\)there exists an element\(g_{\lambda } \in W_{2}^{1} \left[ {0,T} \right]\)such that the functional\(M^{\lambda } \left[ {g,G} \right]\)attains its greatest lower bound.
Proof
We have
A condition for a minimum of this functional is vanishing of its first variation; this is written in the form
by calculating the left-hand side of the above equation and setting \(\epsilon = 0\), we have
By using integration by part for the second term and by setting
we have:
where \(\eta \left( s \right)\) is an arbitrary variation of the function \(g\left( s \right)\) such that both \(g\left( s \right)\) and \(g\left(s \right) + \epsilon \eta \left(s \right)\) belong to the class of admissible functions.
Condition (3.1) will be satisfied for every function \(\eta \left( s \right)\) if
and consistency conditions
Equation (3.2) is called the Euler–Lagrange equation, and the minimizer \(g_{\lambda }\) of Tikhonov functional is determined by the solution of this equation. The solution of Eq. (3.2) with consistency conditions (3.3) is unique based on classical theorems in the ODE.
Now, the regularized solution of the above minimization problem, i.e.,\(g_{\lambda } ,\) is assumed in the form \(g_{\lambda } = R\left( {G,\lambda } \right),\) where \(\lambda = \lambda \left( {\delta ,G_{\lambda \left( \delta \right)} } \right)\), \(R\left( {G,\lambda } \right)\) is a regularizing operator, and \(\delta\) is the error level of input data. The discrete form of Eq. (2.9) based on the proposed numerical algorithm is investigated in Sect. 4.
The collocation method
In this section, we only consider the discrete form of Eq. (2.7) with \(f\left( x \right) = 0\). Since in practical applications, the overspecified condition \(p\left( t \right)\) is given only at mesh points \(t_{i}\) for \(i \, = \, 0, \, 1, \ldots ,n,\) the time interval \(\left[ {0,T} \right]\) is divided into n time intervals by choosing \(t_{0} = 0\), \(t_{n} = T\), and \(t_{i} = i\Delta t,\) where \(\Delta t = \frac{T}{n}\) represents the step size. Now, the overspecified condition (2.5) will be replaced by
The type of discretization of Eq. (2.9) is based on the collocation method. That is an approximate solution \(g\left( t \right)\) to the IHCP (2.1)–(2.5) is expressed as a linear combination of piecewise constant basis functions \(\phi_{i} \left( t \right)\). The approximate solution \(g^{*} \left( t \right)\) of \(g\left( t \right)\) is represented regarding finitely many unknown as follows:
where the basis orthogonal functions \(\phi_{i} \left( t \right)\) are given by
and \(c_{i}\) are unknown coefficients.
Collocating Eq. (4.1) in Eq. (2.9), we obtain
or
Let \(\psi_{i} \left( t \right)\) denote \(\left( {A\phi_{i} } \right)\left( t \right).\) The equality is specified for many values of t; by using the collocation method at discrete points \(t_{j} ,\) we have
or
By the definition of operator integral \(A\) and the basis functions \(\phi_{i} \left( t \right)\) and simple calculations, it is easy to show that
where
and the error function \({\text{erf}}\left( x \right)\) is defined by \(\frac{2}{\sqrt \pi }\mathop \int \nolimits_{0}^{x} {\text{e}}^{{ - u^{2} }} {\text{d}}u\) and \(H\left( t \right)\) is Heaviside function. The ill-conditioned linear system for the determination of the unknown coefficients \(c_{i}\) in Eq. (4.1) is produced by discretization as follows:
where \(A\) is a \(n \times n\) matrix, \(A = \left[ {a_{ij} } \right]\) with entries \(a_{ij} = \psi_{j} \left( {t_{i} } \right)\) for \(i, j = 1, 2, \ldots , n\) and \(G\), \(C\) are \(n\)-dimensional vectors which are defined by:
By the definition of \(\psi_{i} \left( t \right)\), the matrix \(A\) is lower triangular, because
and so the linear system (4.2) can be solved directly. Since the matrix A is ill-conditioned, regularization approach needs to be employed. In Sect. 5, we apply regularization technique and the L-curve and GCV criteria to obtain a stable solution of the system (4.2). By substituting the unknown coefficients into Eq. (4.1), the solution of IHCP can be obtained.
Regularization method for discrete ill-conditioned system
The ill-posedness of the operator integral Eq. (2.9) results in the ill-conditioned system (4.2) from the discretization by the proposed algorithm. Because of the ill-conditionary of matrix A in Eq. (4.2), some type of regularization must then be applied to get stable and accurate results [16,17,18]. For the linear system (4.2), we are faced with the same issues of Hadamard definition, and so we must investigate the sensitivity analysis of solution with respect to random noise in input data \(p\left( t \right)\). In our computation, the zero-order Tikhonov regularization technique is applied to solve the matrix Eq. (4.2).
The regularization method for the discrete ill-posed problem of the form (4.2) is an extension of the least square method (LSM) to find a stable solution for \(AC = G\). The definition of the regularization method is as the following:
Assume \(\lambda > 0\) be a given constant. The Tikhonov regularized solution \(C_{\lambda }\) is the minimizer of the following functional:
provided that a minimizer exists, where \(\left\| . \right\|\) denotes the Euclidean norm and \(\lambda\) is called regularization parameter. (We discussed the existence of minimizer in Sect. 3.)
The choice of suitable value for \(\lambda\) is crucial in this technique since it defined the amount of regularization. Many techniques have been investigated by many scientific researchers to determine a suitable regularization parameter \(\lambda\). In this work, the most well-established techniques for the estimation of \(\lambda\) in Eq. (6.1) are the L-curve and GCV criteria.
-
(I)
L-curve
The L-curve criterion is defined by the log–log plot regularized solution versus the norm of residual and is sketched in the following:
$$L = \left\{ {\left( {\log \left(||{C_{\lambda }||^{2} } \right),\quad \log \left( ||{AC_{\lambda } - G||^{2} } \right)} \right), \quad \lambda > 0} \right\}$$The graph of the curve is as the L-shape and so is called L-curve, and the corner of curve is selected as a suitable regularization parameter \(\lambda\) [18].
-
(II)
GCV
The GCV criterion is an approach for choosing the regularization parameter [18, 19]. The GCV criterion leads to minimization of the following GCV function with respect to \(\lambda\):
$$G\left( \lambda \right) = \frac{||{AC_{\lambda }^{\delta } - G^{\delta}||^2 }}{{\left( {{\text{trace}}\left( {I - AA_{\lambda } } \right)} \right)^{2} }} ,$$where \(A_{\lambda } = \left( {A^{\text{tr}} A + \lambda I} \right)^{ - 1} \cdot A^{\text{tr}}\) is a matrix which produces the regularized solution \(C_{\lambda }^{\delta }\) of Eq. (6.1) from the normal equation
$$\left( {A^{\text{tr}} A + \lambda I} \right)C_{\lambda }^{\delta } = A^{\text{tr}} G^{\delta } .$$
Numerical results and discussion
In this section, to investigate the applicability of the method, a test example is considered. The root-mean-square error (RMSE) is introduced to measure the accuracy as follows:
while \(n + 1\) is the number of collocation points.
Test problem
We consider the problem (2.1)–(2.5) with the following exact solution:
with data
and
which is given by [14]. They have applied a Fourier regularization method for finding the surface heat flux distribution.
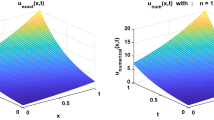
The obtained numerical results obtained for both exact and noisy data are reported.
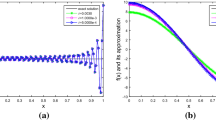
The best regularization parameter by L-curve criteria is represented in Fig. 1. In Fig. 2, the exact solution and the solution obtained using the regularization method with L-curve criteria are plotted when data are exact. The absolute value of error for g(t) without regularization is plotted in Fig. 3.
Results of RMSE value and condition number of matrix A in Eq. (4.2) are reported in Table 1 as the collocation points increase.
The value of the regularization parameter by GCV criteria is shown in Fig. 4. Results of RMSE value and condition number of matrix A in Eq. (4.2) are given in Table 2 as the collocation points increase.
We compare the values of regularization parameters which are obtained by L-curve and GCV and the RMSE value in Table 3 as well.
The stability of the numerical solution with respect to the noisy data \(p_{\delta } \left( t \right)\) is considered by:
where the random('Normal', 0, \(\sigma ,1,N\)) command in MATLAB software generates the random variable from the normal distribution with zero mean and standard deviation \(\sigma\) as the following:
and \(\delta\) represents the percentage of noise.
Table 4 represents the RMSE values of approximation solution in the presence and absence of the regularization method for different values of \(\delta\).
Figure 5 shows the numerical solution of \(g(t)\) by regularization procedure when the input data (2.5) are contaminated by different values of \(\delta\).
Conclusions
In this paper, the spectral collocation method along with Tikhonov regularization technique was successfully applied to the solution of IHCP to determine the unknown heat temperature on the boundary by employing temperature reading at a fixed point. A test example involving different collocation point and measurement errors with noise was considered.
The results show that the approximate solution obtained by the proposed algorithm and using regularization techniques remain stable as the collocation points are increased even when noise is included in the input data.
References
Ramm, A.G.: Inverse Problems: Mathematical and Analytical Techniques with Applications to Engineering. Springer, New York (2005)
Isakov, V.: Inverse Problems for Partial Differential Equations. Springer, New York (1998)
Beck, J.V., Blackwell, B., St. Clair, C.D.: Inverse Heat Conduction: Ill-Posed Problems. Wiley, New York (1985)
Cannon, J.R., Lin, Y., Xu, S.: Numerical procedures for the determination of an unknown coefficient in semi-linear parabolic differential equations. Inverse Probl. 10, 227–243 (1994)
Shidfar, A., Damirchi, J., Reihani, P.: An stable numerical algorithm for identifying the solution of an inverse problem. App. Math. Comput. 190, 231–236 (2007)
Shidfar, A., Karamali, G.R., Damirchi, J.: An inverse heat conduction problem with a nonlinear source term. J. Nonlinear Anal. Theory Methods Appl. 65, 615–621 (2006)
Shidfar, A., Paryab, K., Yazdanian, A.R.: On Tikhonov regularization method in calibration of volatility term-structure. Inf. Sci. Lett. 2, 93–100 (2013)
Rashedi, K., Adibi, H., Dehghan, M.: Determination of space time-dependent heat source in a parabolic inverse problem via the Ritz–Galerkin technique. Inverse Probl. Sci. Eng. 22, 1077–1086 (2014)
Yan, L., Fu, C.L., Yang, F.L.: The method of fundamental solution for the inverse source problem. Eng. Anal. Bound. Elem. 32, 216–222 (2008)
Duda, P.: Numerical and experimental verification of two methods for solving an inverse heat conduction problem. Int. J. Heat Mass Transf. 84, 1101–1112 (2015)
Miao, C., Yang, K., Xu, X.L., Wang, S.D., Gao, X.W.: A modified Levenberg–Marquardt algorithm for simultaneous estimation of multi-parameters of boundary heat flux by solving transient nonlinear inverse heat conduction problems. Int. J. Heat Mass Transf. 97, 908–916 (2016)
Garshasbi, M., Dastour, H.: Estimation of unknown boundary functions in an inverse heat conduction problem using a mollified marching scheme. Numer. Algorithms 68, 769–790 (2015)
Masanori, M., Arima, H., Mitsutake, Y.: Estimation of surface temperature and heat flux using inverse solution for one-dimensional heat conduction. J. Heat Transf. 125, 213–223 (2003)
Fu, C.L., Xiong, X.T., Fu, P.: Fourier regularization method for solving the surface heat flux from interior observations. Math. Comput. Model. 42, 489–498 (2005)
Cannon, J.R.: The One Dimensional Heat Equation. Addison-Wesley, New York (1984)
Tikhonov, A.N., Arsenin, V.Y.: Solution of Ill-Posed Problems. VH Winston & Sons, Washington D.C. (1997)
Engl, H.W., Hanke, M., Neubauer, A.: Regularization of the Inverse Problems. Kluwer Academic Publishers, Dordrecht (1996)
Hansen, P.C.: Analysis of discrete ill-posed problem by means of the L-curve. KSIAM Rev. 34, 561–580 (1992)
Hansen, P.C.: Regularization tools: a Matlab package for analysis and solution of discrete ill-posed problems. Numer. Algorithms 6, 1–35 (1994)
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Damirchi, J., Yazdanian, A.R., Shamami, T.R. et al. Numerical investigation of an inverse problem based on regularization method. Math Sci 13, 193–199 (2019). https://doi.org/10.1007/s40096-019-0288-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40096-019-0288-2