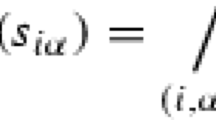Certain algebraic structures associated with a double fuzzy topological space

Abstract

The algebraic structures of the families of fuzzy sets that arise out of various notions of openness and closedness in a double fuzzy topological space are investigated. The collection of these families forms a bounded, associative lattice. The zero divisors and zero-divisor graph of this lattice are also identified.

Introduction

Attanassov introduced the concept of intuitionistic fuzzy sets in [1]. Subsequently, the concept of intuitionistic fuzzy topological spaces was introduced by Çoker [2].

Later, Lee and Im [3] initiated the concept of mated fuzzy topological spaces, as a generalization of intuitionistic fuzzy topological spaces introduced in [2] and smooth fuzzy topological spaces. Also, they presented the notions of (p, q)-fuzzy open set, (p, q)-fuzzy closed set, closure operator and interior operator in mated fuzzy topological spaces. Again, in 2005, Ramadan et al. [4] ushered in the concept of (p, q)-regular fuzzy open sets and (p, q)-regular fuzzy closed sets in intuitionistic fuzzy topological spaces.

Later, the notions of (p, q)-generalized fuzzy open and (p, q)-generalized fuzzy closed sets, (p, q)-regular generalized fuzzy open and (p, q)-regular generalized fuzzy closed sets, (p, q)-fuzzy b-open and (p, q)-fuzzy b-closed sets and (p, q)-generalized fuzzy b-open and (p, q)-generalized fuzzy b-closed sets in intuitionistic fuzzy topological spaces were set up and studied in [5] and [6]. These sets were further explored in [7,8,9,10].

In [11], Gutierrez Garcia and Rodabaugh suggested that the term “double fuzzy sets" is more appropriate than “intuitionistic fuzzy sets". Therefore, we proceed by using the term “double fuzzy topological space" instead of “intuitionistic fuzzy topological space."

This paper studies the structural properties of certain families of fuzzy open sets and fuzzy closed sets in a double fuzzy topological space. As a result, it is identified that the collections $G{\mathcal {O}}_{F,p,q}$ of (p, q)-generalized fuzzy open sets, $G{\mathcal {C}}_{F,p,q}$ of (p, q)-generalized fuzzy closed sets, $G{\mathcal {O}}'_{F,p,q}$ of (p, q)-regular generalized fuzzy open sets and $G{\mathcal {C}}'_{F,p,q}$ of (p, q)-regular generalized fuzzy closed sets are monoids. Further, the monoid structure of the collections $b{\mathcal {C}}_{F,p,q}$ of (p, q)-fuzzy b-closed sets and $b{\mathcal {O}}_{F,p,q}$ of (p, q)-fuzzy b-open sets is also identified. But, $Gb{\mathcal {O}}_{F,p,q}$ and $Gb{\mathcal {C}}_{F,p,q},$ the collections of (p, q)-generalized fuzzy b-open sets and (p, q)-generalized fuzzy b-closed sets, respectively, have no such structure in general. Above all, a lattice ${\mathbb {L}}_{p,q}^F$ consisting of various families of fuzzy sets engendered by different notions of openness and closedness in a double fuzzy topological space is obtained. While ${\mathbb {L}}_{p,q}^F$ is associative and complemented, it is not distributive and hence not modular. The study also analyzes the zero divisors of ${\mathbb {L}}_{p,q}^F$ and its zero divisor graph.

Preliminaries

Throughout the paper, X denotes a nonempty set, $I =[0, 1],$$I_0 =(0, 1],~ I_1 =[0, 1),~ I^X =$ the set of all fuzzy subsets of X. The constant fuzzy subset taking the value $\alpha$ is denoted by $\underline{\alpha }$. Also, the complement of a fuzzy set f is denoted by $f^c$.

Definition 2.1

(see [12]) Consider the pair $(F, F^*)$ of functions from $I^X \rightarrow I$ such that

• 1. $\displaystyle F(f) + F^*(f)\le 1, \forall f\in I^X$

• 2. $\displaystyle F(\underline{0})=F(\underline{1})=1, F^*(\underline{0})=F^*(\underline{1})=0$

• 3. $\displaystyle F(f_1 \wedge f_2)\ge F(f_1)\wedge F(f_2)$ and $\displaystyle F^*(f_1 \wedge f_2)\le F^*(f_1)\vee F^*(f_2), f_i\in I^X, i=1, 2$

• 4. $\displaystyle F(\bigvee _{i\in \Delta } f_i)\ge \bigwedge _{i\in \Delta } F(f_i)$ and $\displaystyle F^*(\bigvee _{i\in \Delta } f_i) \le \bigvee _{i\in \Delta } F^*(f_i), f_i \in I^X, i \in \Delta$

The pair $(F,F^*)$ is called a double fuzzy topology on X. The triplet $(X, F, F^*)$ is called a double fuzzy topological space(for short dfts).

Definition 2.2

(see [3]) Let $(X,F,F^*)$ be a dfts. For each $p\in I_0,q\in I_1, f\in I^X,$ the operator $C_{F,F^*}: I^X \times I_0 \times I_1 \rightarrow I^X$ defined by

$$\begin{aligned} C_{F,F^*}(f, p,q) =\bigwedge \{g \in I^X |f\le g, F(g^c)\ge p, F^*(g^c)\le q\} \end{aligned}$$

is called the double fuzzy closure operator on $(X,F,F^*)$.

Definition 2.3

(see [3]) Let $(X,F,F^*)$ be a dfts. For each $p\in I_0,q\in I_1, f\in I^X,$ the operator $I_{F,F^*}: I^X \times I_0 \times I_1 \rightarrow I^X$ defined by

$$\begin{aligned} I_{F,F^*}(f, p,q)=\bigvee \{g \in I^X |f\ge g, F(g)\ge p, F^*(g)\le q\}\end{aligned}$$

is called the double fuzzy interior operator on $(X,F,F^*)$.

Definition 2.4

(see [13]) For $x\in X$ and $\lambda \in I_0,$ the fuzzy point $x_\lambda$ denotes the fuzzy set

$$\begin{aligned} x_\lambda (y)=\left\{ \begin{array}{ll}\lambda ,& \quad \hbox {if }y=x\\ 0, & \quad \hbox {otherwise}\end{array}\right. \end{aligned}$$

Definition 2.5

(see [14]) A poset L is called

• 1. A join semi-lattice if $x\vee y\in L$ for all $x,y\in L$.

• 2. A meet semi-lattice if $x\wedge y\in L$ for all $x,y\in L.$

L is called a lattice if it is both a join semi-lattice and a meet semi-lattice.

Definition 2.6

A monoid is a set X with a binary operation $*:X\times X\rightarrow X$ which is associative and has an identity element.

Lee and Im [3] introduced (p, q)-fuzzy open sets and (p, q)-fuzzy closed sets in mated fuzzy topological spaces which in the context of a dfts takes the following form:

Definition 2.7

(see [3]) Let $(X, F, F^*)$ be a dfts. A fuzzy set f is said to be

• (i) (p, q)-fuzzy open if $F(f)\ge p$ and $F^*(f)\le q$ and

• (ii) (p, q)-fuzzy closed if $f^c$ is (p, q)-fuzzy open.

Definition 2.8

(see [4]) Let $(X,F,F^*)$ be a dfts, $f\in I^X , p\in I_0$ and $q\in I_1$. Then, f is called

• (i) (p, q)-regular fuzzy open (for short (p, q)-rfo) if $f = I_{F,F^*}\big (C_{F,F^*}(f, p,q), p,q\big ).$

• (ii) (p, q)-regular fuzzy closed (for short (p, q)-rfc) if $f = C_{F,F^*}\big (I_{F,F^*}(f, p,q), p,q\big ).$

Notation With respect to a dfts $(X,F,F^*)$ and $p\in I_0, q\in I_1$ with $p+q\le 1,$ we use the following notations:

• ${\mathcal {O}}_{F,p,q} = \{f\in I^X : f$ is a (p, q)-fuzzy open set},

• ${\mathcal {C}}_{F,p,q} = \{f\in I^X : f^c\in O_{F,p,q}\},$

• ${\mathcal {L}}_{F,p,q} = {\mathcal {O}}_{F,p,q}\cap {\mathcal {C}}_{F,p,q},$

• ${\mathcal {O}}'_{F,p,q} = \{f\in I^X: f$ is a (p, q)-rfo set} and

• ${\mathcal {C}}'_{F,p,q} = \{f\in I^X: f^c \in {\mathcal {O}}'_{F,p,q}\}$

Abbas [5] introduced the concept of (p, q)-generalized fuzzy closed sets in a dfts as the following:

Definition 2.9

(see [5]) Let $(X,F,F^*)$ be a dfts, $f,h\in I^X , p\in I_0$ and $q\in I_1,$ then f is said to be

• (i) (p, q)-generalized fuzzy closed (for short, (p, q)-gfc) set if $C_{F,F^*}(f, p,q) \le h$ whenever $f\le h$ and $h \in {\mathcal {O}}_{F,p,q}$ and

• (ii) (p, q)-generalized fuzzy open (for short, (p, q)-gfo) set if $f^c$ is a (p, q)-gfc set.

The collection of all (p, q)-gfc sets is denoted by $G{\mathcal {C}}_{F,p,q},$ and the collection of all (p, q)-gfo sets is denoted by $G{\mathcal {O}}_{F,p,q}$.

The concept of (p, q)-regular generalized fuzzy closed sets was also introduced by Abbas in [5].

Definition 2.10

(see [5]) Let $(X,F,F^*)$ be a dfts, $f,h\in I^X , p\in I_0$ and $q\in I_1$ with $p+q\le 1,$ then f is called

• (i) (p, q)-regular generalized fuzzy closed (for short, (p, q)-rgfc) set if $C_{F,F^*}(f, p,q) \le h$ whenever $f\le h$ and $h\in {\mathcal {O}}'_{F,p,q}$ and

• (ii) (p, q)-regular generalized fuzzy open (for short, (p, q)-rgfo) set if $f^c$ is a (p, q)-gfc set.

The collection of all (p, q)-rgfc sets is denoted by $G{\mathcal {C}}'_{F,p,q},$ and the collection of all (p, q)-rgfo sets is denoted by $G{\mathcal {O}}'_{F,p,q}$.

Mohammed et al. [6] introduced the concepts of (p, q)-fuzzy b-closed sets and (p, q)-fuzzy b-open sets in a dfts and studied various properties of them.

Definition 2.11

(see [6]) Let $(X,F,F^*)$ be a dfts. A fuzzy set f is called

• (i) (p, q)-fuzzy b-closed (for short, (p, q)-fbc) if

  $$\begin{aligned}&\left( I_{F,F^*}\left( C_{F,F^*}(f,p,q),p,q\right) \right) \\&\quad \wedge \left( C_{F,F^*}\left( I_{F,F^*}(f,p,q),p,q\right) \right) \le f \end{aligned}$$

• (ii) (p, q)-fuzzy b-open (for short, (p, q)-fbo) iff $f^c$ is (p, q)-fbc set.

For a dfts $(X,F,F^*),$ the collection of all (p, q)-fbo is denoted by $b{\mathcal {O}}_{F,p,q}$ and the collection of all (p, q)-fbc is denoted by $b{\mathcal {C}}_{F,p,q}$.

In [6], the authors also introduced the concepts (p, q)-generalized fuzzy b-closed sets and (p, q)-generalized fuzzy b-open sets in terms of the double fuzzy b-closure and double fuzzy b-interior operators defined as follows:

Definition 2.12

(see [6]) Let $(X, F, F^*)$ be a dfts. Then, the b-closure and b-interior operators in $(X, F, F^*)$ are defined by $bC_{F,F^*}(f, p,q) = \wedge \{h\in I^X: f\le h \text{ and } h \text{ is } (p,q)\text{-fbc }\}$ and $bI_{F,F^*}(f, p,q) = \vee \{h\in I^X: h\le f \text{ and } h \text{ is } (p,q)\text{-fbo }\}$ where $p\in I_0$ and $q\in I_1$ such that $p+q\le 1$.

Definition 2.13

(see [6]) Let $(X,F,F^*)$ be a dfts, $f\in I^X , p\in I_0$ and $q\in I_1$ with $p+q\le 1,$ then f is called

• (i) (p, q)-generalized fuzzy b-closed (for short (p, q)-gfbc) set if $bC_{F,F^*}(f, p,q) \le h$ whenever $f\le h$ and $h\in {\mathcal {O}}_{F,p,q}$ and

• (ii) (p, q)-generalized fuzzy b-open (for short (p, q)-gfbo) set if $f^c$ is a (p, q)-gfc set.

The collection of all (p, q)-gfbc sets is denoted by $Gb{\mathcal {C}}_{F,p,q},$ and the collection of all (p, q)-gfbo sets is denoted by $Gb{\mathcal {O}}_{F,p,q}$.

Pu and Liu defined the concept of quasi-coincidence as follows:

Definition 2.14

(see [15]) If $f,g\in I^X$ be such that $f(y) + g(y) > 1$ for some $y\in X,$ then f is said to be quasi-coincident with g, represented by fqg. The negation of fqg is denoted by $f\overline{q}g$.

Definition 2.15

(see [16]) Let $(X,F,F^*)$ be a dfts. If for each $f_1,f_2\in I^X,$$p\in I_0$ and $q\in I_1$ such that $f^c_1,f^c_2\in {\mathcal {C}}_{F,p,q}$ and $f_1 \overline{q}f_2,$ there exist $g_1,g_2\in {\mathcal {O}}_{F,p,q}$ such that $f_1 \le g_1, f_2 \le g_2$ and $g_1 \overline{q}g_2,$ then $(X,F,F^*)$ is called a double fuzzy normal space.

Definition 2.16

(see [17]) Let $(X,F,F^*)$ be a dfts. Then, for $p\in I_0$ and $q\in I_1,$$(XF,F^*)$ is called (p, q)-connected if there does not exist $f_1, f_2\in I^X\setminus \{\underline{0}\}$ such that $f_1 \vee f_2=\underline{1}$ and $C_{F,F^*} ( f_1, p,q) \wedge f_2 = C_{F,F^*} ( f_2, p,q) \wedge f_1 = \underline{0}$.

Equivalently, for $p\in I_0$ and $q\in I_1,$$(X,F,F^*)$ is called (p, q)-connected if and only if there does not exist $f_1, f_2\in {\mathcal {C}}_{F,p,q}$ such that $f_1 \vee f_2=\underline{1}$ and $f_1 \wedge f_2 = \underline{0}$.

Definition 2.17

(see [18]) Let L be a lattice. Then, $a \in L$ is called a zero divisor of L if there exists a nonzero element b in L such that $a \wedge b = 0$.

The set of all zero divisors of L is represented by Z(L).

Theorem 2.18

(see [19]) Let$(X,F,F^*)$be a dfts. Then, ${\mathcal {L}}_{F,p,q}$is a Booleanalgebra if and only if${\mathcal {L}}_{F,p,q}\subseteq \left\{ \chi _A: A\subseteq X\right\}$.

Regular generalized fuzzy closed sets and regular generalized fuzzy open sets

This section investigates the algebraic structures associated with $G{\mathcal {C}}_{F,p,q},$$G{\mathcal {O}}_{F,p,q}, G{\mathcal {C}}'_{F,p,q}$ and $G{\mathcal {O}}'_{F,p,q}$.

Theorem 3.1

${\mathcal {C}}'_{F,p,q}\subseteq {\mathcal {C}}_{F,p,q}\subseteq G{\mathcal {C}}_{F,p,q}$and${\mathcal {O}}'_{F,p,q}\subseteq {\mathcal {O}}_{F,p,q}\subseteq G{\mathcal {O}}_{F,p,q}$.

Proof

$$\begin{aligned} f\in {\mathcal {C}}'_{F,p,q} & \Rightarrow C_{F,F^*}\big (I_{F,F^*}(f, p,q), p,q\big )=f\\\ & \Rightarrow F(f^c)\ge p \text{ and } F^*(f^c)\le q\\ & \Rightarrow f\in {\mathcal {C}}_{F,p,q,}\\ \hbox {Again, }f\in {\mathcal {C}}_{F,p,q} & \Rightarrow F(f^c)\ge p \text{ and } F^*(f^c)\le q\\ &\Rightarrow C_{F,F^*}(f, p,q) =f\\ &\Rightarrow C_{F,F^*}(f, p,q)\le h\hbox { whenever }f\le h\hbox { and }h\in {\mathcal {O}}_{F,p,q}\\ &\Rightarrow f\in G{\mathcal {C}}_{F,p,q,} \end{aligned}$$

i.e., ${\mathcal {C}}'_{F,p,q}\subseteq {\mathcal {C}}_{F,p,q}\subseteq G{\mathcal {C}}_{F,p,q}$.

Consequently, ${\mathcal {O}}'_{F,p,q}\subseteq {\mathcal {O}}_{F,p,q}\subseteq G{\mathcal {O}}_{F,p,q}$. $\square$

The following theorem elucidates the structure of $G{\mathcal {C}}_{F,p,q}$ and $G{\mathcal {O}}_{F,p,q}$.

Theorem 3.2

$G{\mathcal {C}}_{F,p,q}$ is a join semi-lattice, and $G{\mathcal {O}}_{F,p,q}$ is a meet semi-lattice.

Proof

Consider $f_1, f_2\in G{\mathcal {C}}_{F,p,q}$ and $h\in {\mathcal {O}}_{F,p,q}$ such that $f_1\vee f_2\le h$. Then, since $f_1\le h$ and $f_1\in G{\mathcal {C}}_{F,p,q},$$C_{F,F^*}(f_1,p,q)\le h$. Similarly, $C_{F,F^*}(f_2,p,q)\le h$.

Therefore, $C_{F,F^*}(f_1\vee f_2,p,q)=C_{F,F^*}(f_1,p,q)\vee C_{F,F^*}(f_2,p,q)\le h$.

Hence, $f_1\vee f_2\in G{\mathcal {C}}_{F,p,q},$ i.e., $G{\mathcal {C}}_{F,p,q}$ is a join semi-lattice.

Further,

$$\begin{aligned} f_1, f_2\in G{\mathcal {O}}_{F,p,q}&\Rightarrow f_1^c, f_2^c\in G{\mathcal {C}}_{F,p,q}\\&\Rightarrow f_1^c\vee f_2^c\in G{\mathcal {C}}_{F,p,q}\\&\Rightarrow (f_1\wedge f_2)^c\in G{\mathcal {C}}_{F,p,q}\\&\Rightarrow f_1\wedge f_2\in G{\mathcal {O}}_{F,p,q}. \end{aligned}$$

Hence, $G{\mathcal {O}}_{F,p,q}$ is a meet semi-lattice. $\square$

Corollary 3.3

$G{\mathcal {C}}_{F,p,q}$and$G{\mathcal {O}}_{F,p,q}$are monoids.

Proof

By Theorem 3.2, $G{\mathcal {C}}_{F,p,q}$ is a join semi-lattice and $G{\mathcal {O}}_{F,p,q}$ is a meet semi-lattice.

Also, $\underline{0}$ and $\underline{1}$ are the identities of $G{\mathcal {C}}_{F,p,q}$ and $G{\mathcal {O}}_{F,p,q},$ respectively. $\square$

The following example illustrates that $G{\mathcal {C}}_{F,p,q}$ need not be a meet semi-lattice and $G{\mathcal {O}}_{F,p,q}$ need not be a join semi-lattice.

Example 3.4

Let $X=I$ and define a double fuzzy topology $(F,F^*)$ on X as follows:

$$\begin{aligned}& F(f)=\left\{ \begin{array}{ll} 1,& \quad \hbox {if } f\in \{\underline{0}, \underline{1}\}\\ \frac{13}{20}, &\quad \hbox {if } f\in {\mathcal {A}}\\ \frac{7}{10}, & \quad \hbox {if } f\in {\mathcal {B}}\\ 0,& \quad \hbox {otherwise.} \end{array}\right. \hbox { and }\\&F^*(f)=\left\{ \begin{array}{ll} 0,&\quad \hbox {if } f\in \{\underline{0}, \underline{1}\}\\ \frac{3}{10},&\quad \hbox {if } f\in {\mathcal {A}}\\ \frac{11}{50},&\quad \hbox {if } f\in {\mathcal {B}}\\ 1,&\quad \hbox {otherwise.} \end{array}\right. \end{aligned}$$

where ${\mathcal {A}}=\left\{ (\underline{\frac{1}{3}}), (\underline{\frac{1}{2}}), (\underline{\frac{3}{5}}), (\underline{\frac{3}{4}})\right\}$ and

$$\begin{aligned} {\mathcal {B}} &= \left\{ \left( \frac{11}{20}\right) _{\frac{7}{20}},\left( \frac{11}{20}\right) _{\frac{1}{3}}, \left( \frac{11}{20}\right) _{\frac{7}{20}}\vee \left( \underline{\frac{1}{3}}\right) , \left( \frac{11}{20}\right) _{\frac{7}{20}}^c,\right. \\&\quad \left. \left( \frac{11}{20}\right) _{\frac{7}{20}}^c\wedge \left( \underline{\frac{3}{4}}\right) , \left( \frac{11}{20}\right) _{\frac{1}{4}}^c\right\} \end{aligned}$$

Let $p=\frac{13}{20}$ and $q=\frac{3}{10}$. Then,

$$\begin{aligned}&{\mathcal {O}}_{F,p,q}=\left\{ \underline{0}, \underline{1}\right\} \cup {\mathcal {A}}\cup {\mathcal {B}},\hbox { and }\\&{\mathcal {C}}_{F,p,q}=\left\{ f^c:f\in {\mathcal {O}}_{F,p,q}\right\} , \end{aligned}$$

Now,

$$\begin{aligned} C_{F,F^*}(f,p,q)=\left\{ \begin{array}{ll} \underline{0}, &\text{ if } f=\underline{0}\\ \left( \frac{11}{20}\right) _{\frac{1}{4}}, &\quad \hbox {if } f\le \left( \frac{11}{20}\right) _{\frac{1}{4}}\\ \left(\underline{\frac{1}{4}}\right), &\quad \hbox {if }f\le \left(\underline{\frac{1}{4}}\right) {\text{ and }} f\nleq \left( \frac{11}{20}\right) _{\frac{1}{4}}\\ \left( \frac{11}{20}\right) _{\frac{7}{20}}, & \quad \hbox {if }\left( \frac{11}{20}\right) _{\frac{1}{4}}\lneq f\le \left( \frac{11}{20}\right) _{\frac{7}{20}}\\ \left( \frac{11}{20}\right) _{\frac{7}{20}}\vee \left(\underline{\frac{1}{4}}\right), &\quad \hbox {if }f\le \left( \frac{11}{20}\right) _{\frac{7}{20}}\vee \left(\underline{\frac{1}{4}}\right), f\nleq \left(\underline{\frac{1}{4}}\right) \hbox { and } f\nleq \left( \frac{11}{20}\right) _{\frac{7}{20}}\\ \left(\underline{\frac{2}{5}}\right), &\quad \hbox {if }f\le \left(\underline{\frac{2}{5}}\right)\hbox { and }f\nleq \left( \frac{11}{20}\right) _{\frac{7}{20}}\vee \left(\underline{\frac{1}{4}}\right)\\ \left(\underline{\frac{1}{2}}\right), &\quad \hbox {if }f\le \left(\underline{\frac{1}{2}}\right)\hbox { and }f\nleq \left(\underline{\frac{2}{5}}\right)\\ \left( \frac{11}{20}\right) _{\frac{7}{20}}^c\wedge \left(\underline{\frac{2}{3}}\right), &\quad \hbox {if }f\le \left( \frac{11}{20}\right) _{\frac{7}{20}}^c\wedge \left(\underline{\frac{2}{3}}\right)\hbox { and }f\nleq \left(\underline{\frac{1}{2}}\right)\\\left(\underline{\frac{2}{3}}\right), &\quad \hbox {if }f\le \left(\underline{\frac{2}{3}}\right)\hbox { and }f\nleq \left( \frac{11}{20}\right) _{\frac{7}{20}}^c\wedge \left(\underline{\frac{2}{3}}\right)\\ \left( \frac{11}{20}\right) _{\frac{7}{20}}^c, &\quad \hbox {if }f\le \left( \frac{11}{20}\right) _{\frac{7}{20}}^c, \; f\nleq \left( \frac{11}{20}\right) _{\frac{7}{20}}^c\wedge \left(\underline{\frac{2}{3}}\right)\\ \left( \frac{11}{20}\right) _{\frac{1}{3}}^c, &\quad \hbox {if }f\le \left( \frac{11}{20}\right) _{\frac{1}{3}}^c\hbox { and }f\nleq \left( \frac{11}{20}\right) _{\frac{7}{20}}^c\\ \underline{1}, &\quad \hbox {otherwise. } \end{array} \right. \end{aligned}$$

Also,

$$\begin{aligned} G{\mathcal {C}}_{F,p,q} &= \left\{ f:0\le f\le \left( \underline{\frac{1}{4}}\right) \text{ OR } \left( \frac{11}{20}\right) _{\frac{1}{3}}\lneq f\le \left( \frac{11}{20}\right) _{\frac{7}{20}} \text{ OR } \right. \\&\quad\left( \frac{11}{20}\right) _{\frac{1}{3}}\vee \left( \underline{\frac{1}{4}}\right) \lneq f\le \left( \frac{11}{20}\right) _{\frac{7}{20}}\vee \left( \underline{\frac{1}{4}}\right) \text{ OR } f\le \left( \underline{\frac{1}{2}}\right) \text{ and }\\&\quad f\nleq \left( \frac{11}{20}\right) _{\frac{7}{20}}\vee \left( \underline{\frac{1}{3}} \right) \text{ OR } f\le \left( \frac{11}{20}\right) _{\frac{7}{20}}^c\wedge \left( \underline{\frac{2}{3}}\right) \text{ and }\\& \quad f\nleq \left( \underline{\frac{3}{5}}\right) \text{ OR } f\le \left( \frac{11}{20}\right) _{\frac{1}{3}}^c \text{ and } f\nleq \left( \frac{11}{20}\right) _{\frac{7}{20}}^c\wedge \left( \underline{\frac{3}{4}}\right) \text{ OR }\\&\quad f\le \underline{1} \text{ with } \left. f\left(\frac{11}{20}\right)>\frac{3}{4}\right\} \end{aligned}$$

and $G{\mathcal {O}}_{F,p,q}=\left\{ f:f^c\in G{\mathcal {C}}_{F,p,q}\right\}$.

Now, consider the fuzzy set $f\in I^X$ defined by

$$f(x)=\left\{ \begin{array}{ll}\frac{9}{25},&\quad \text{ if } x\ne \frac{11}{20}\\ \frac{3}{10},&\quad \text{ if } x= \frac{11}{20} \end{array}\right. .$$

It is clear that $f, (\frac{11}{20})_{\frac{7}{20}}\in G{\mathcal {C}}_{F,p,q}$ and $f^c, (\frac{11}{20})^c_{\frac{7}{20}}\in G{\mathcal {O}}_{F,p,q}$. But, $f\wedge (\frac{11}{20})_{\frac{7}{20}}=(\frac{11}{20})_{\frac{3}{10}}\not \in G{\mathcal {C}}_{F,p,q}$ and $f^c\vee (\frac{11}{20})^c_{\frac{7}{20}}=(\frac{11}{20})^c_{\frac{3}{10}}\not \in G{\mathcal {O}}_{F,p,q}$.

Generally, $G{\mathcal {C}}_{F,p,q}$ is not closed under arbitrary join and $G{\mathcal {O}}_{F,p,q}$ is not closed under arbitrary meet as seen in the following.

Example 3.5

Let $X=\{c,d\}$ and define a double fuzzy topology $(F,F^*)$ on X as follows:

$$\begin{aligned} F(f)=\left\{ \begin{array}{ll} 1, &\quad \text{ if } f\in \{\underline{0}, \underline{1}\}\\ \alpha , &\quad \text{ if } f=\underline{\alpha }, \alpha \in \left( \frac{3}{5},\frac{3}{4}\right] \\ \frac{1}{2},&\quad \text{ if } f=\left( \underline{\frac{9}{20}}\right) \\ 0,&\quad \text{ otherwise. } \end{array}\right. \qquad \hbox { and }\qquad F^*(f)=\left\{ \begin{array}{ll} 0,&\quad \text{ if } f\in \{\underline{0}, \underline{1}\}\\ \frac{1}{5},&\quad \text{ if } f=\underline{\alpha }, \alpha \in \left( \frac{3}{5},\frac{3}{4}\right] \\ \frac{1}{4},&\quad \text{ if } f=\left( \underline{\frac{9}{20}}\right) \\ 1,&\quad \text{ otherwise. } \end{array}\right. \end{aligned}$$

Let $p=\frac{1}{2}$ and $q=\frac{1}{4}$. Clearly, ${\mathcal {O}}_{F,p,q}=\{\underline{0}, \underline{1}\}\cup \left\{ \underline{\alpha }: \alpha \in (\frac{3}{5},\frac{3}{4}] \text{ or } \alpha = \frac{9}{20}\right\}$ and

$$\begin{aligned}G{\mathcal {C}}_{F,p,q}=\left\{ f: \underline{0}\le f\lneq \left( \underline{\frac{2}{5}}\right) \text{ with } f(x)\lneq \frac{2}{5} {\text{ for all }} x\in X \text{ OR } \right. \\ \left. f\le \left( \underline{\frac{11}{20}}\right) \text{ and } f\nleq \left( \underline{\frac{9}{20}}\right) \text{ OR } f\le \underline{1} \text{ and } f\nleq \left( \underline{\frac{3}{4}}\right) \right\} .\end{aligned}$$

Then, for the collection ${\mathcal {F}}=\left\{ f: \underline{0}\le f\lneq (\underline{\frac{2}{5}}) \text{ with } f(x)\lneq \frac{2}{5} {\text{ for all }} x\in X\right\} \subseteq G{\mathcal {C}}_{F,p,q},$${\displaystyle \bigvee _{f\in {\mathcal {F}}}}f=(\underline{\frac{2}{5}})\not \in G{\mathcal {C}}_{F,p,q},$ which shows that $G{\mathcal {C}}_{F,p,q}$ is not closed under arbitrary join. Further, $G{\mathcal {O}}_{F,p,q}$ is not closed under arbitrary meet since ${\displaystyle \bigwedge _{f\in {\mathcal {F}}}}f^c=(\underline{\frac{3}{4}})\not \in G{\mathcal {O}}_{F,p,q},$ where $\{f^c: f\in {\mathcal {F}}\}\subseteq G{\mathcal {O}}_{F,p,q}$.

In the remaining part of this section, we concentrate on the families $G{\mathcal {C}}'_{F,p,q}$ and $G{\mathcal {O}}'_{F,p,q}$.

Clearly, $G{\mathcal {C}}_{F,p,q}\subseteq G{\mathcal {C}}'_{F,p,q}$ and $G{\mathcal {O}}_{F,p,q}\subseteq G{\mathcal {O}}'_{F,p,q}$.

The following theorem shows that $G{\mathcal {C}}'_{F,p,q}$ and $G{\mathcal {O}}'_{F,p,q}$ admit the same structure of $G{\mathcal {C}}_{F,p,q}$ and $G{\mathcal {O}}_{F,p,q},$ respectively.

Theorem 3.6

$G{\mathcal {C}}'_{F,p,q}$ is a join semi-lattice, and $G{\mathcal {O}}'_{F,p,q}$ is a meet semi-lattice.

Proof

Consider $f_1, f_2\in G{\mathcal {C}}'_{F,p,q}$ and $h\in {\mathcal {O}}'_{F,p,q}$ such that $f_1\vee f_2\le h$. Then, since $f_1\le h$ and $f_1\in G{\mathcal {C}}'_{F,p,q},$$C_{F,F^*}(f_1,p,q)\le h$. Similarly, $C_{F,F^*}(f_2,p,q)\le h$. Therefore, $C_{F,F^*}(f_1\vee f_2,p,q)=C_{F,F^*}(f_1,p,q)\vee C_{F,F^*}(f_2,p,q)\le h,$

i.e., $f_1\vee f_2\in G{\mathcal {C}}'_{F,p,q},$ and hence, $G{\mathcal {C}}'_{F,p,q}$ is a join semi-lattice.

$$\begin{aligned}\text{ Further, } &f_1, f_2\in G{\mathcal {O}}'_{F,p,q}\\&\quad \Rightarrow f_1^c\vee f_2^c\in G{\mathcal {C}}'_{F,p,q} {\text{ by Theorem 3.6. }}\\&\quad \Rightarrow (f_1\wedge f_2)^c\in G{\mathcal {C}}'_{F,p,q}\\&\quad \Rightarrow f_1\wedge f_2\in G{\mathcal {O}}'_{F,p,q}. \end{aligned}$$

Hence, $G{\mathcal {O}}'_{F,p,q}$ is a meet semi-lattice. $\square$

Corollary 3.7

$G{\mathcal {C}}'_{F,p,q}$and$G{\mathcal {O}}'_{F,p,q}$are monoids.

The following example demonstrates that $G{\mathcal {C}}'_{F,p,q}$ need not be a meet semi-lattice and $G{\mathcal {O}}'_{F,p,q}$ need not be a join semi-lattice.

Example 3.8

Consider the dfts defined in Example 3.4. Then, for $p=\frac{13}{20}$ and $q=\frac{3}{10},$ we have ${\mathcal {O}}'_{F,p,q}=\left\{ \underline{0}, \underline{1}, (\underline{\frac{1}{2}}), (\underline{\frac{3}{5}}), \left( \frac{11}{20}\right) _{\frac{7}{20}}, \left( \frac{11}{20}\right) _{\frac{7}{20}}^c, \left( \frac{11}{20}\right) _{\frac{7}{20}}\vee (\underline{\frac{1}{3}})\right\}$ and ${\mathcal {C}}'_{F,p,q}=\left\{ \underline{0}, \underline{1}, (\underline{\frac{1}{2}}), (\underline{\frac{2}{5}}), \left( \frac{11}{20}\right) _{\frac{7}{20}},\left( \frac{11}{20}\right) _{\frac{7}{20}}^c, \left( \frac{11}{20}\right) _{\frac{7}{20}}^c\wedge (\underline{\frac{2}{3}})\right\}$.

Hence,

$$\begin{aligned} G{\mathcal {C}}'_{F,p,q} =& \left\{ f: \underline{0}\le f\le \left( \frac{11}{20}\right) _{\frac{7}{20}}\vee \left( \underline{\frac{1}{4}}\right) \text{ OR } f\le \left( \underline{\frac{1}{2}}\right) \text{ and } \right. \\ & \left. f\nleq \left( \frac{11}{20}\right) _{\frac{7}{20}}\vee \left( \underline{\frac{1}{3}}\right) \text{ OR } f\le \underline{1} \text{ and } f\nleq \left( \underline{\frac{3}{5}}\right) \right\} \end{aligned}$$

and $G{\mathcal {O}}'_{F,p,q}=\left\{ f:f^c\in G{\mathcal {C}}'_{F,p,q}\right\}$.

Now, consider $f\in I^X$ defined in Example 3.4. Also, let $g(x)=\left\{ \begin{array}{ll}\frac{3}{10},&\text{ if } x\ne \frac{11}{20}\\ \frac{9}{25},&\text{ if } x= \frac{11}{20} \end{array}\right.$. Then, it is clear that $f, g\in G{\mathcal {C}}'_{F,p,q}$. But, $f\wedge g=(\underline{\frac{3}{10}})\not \in G{\mathcal {C}}'_{F,p,q}$.

Subsequently, $f^c, g^c\in G{\mathcal {O}}'_{F,p,q}$. But, $f^c\vee g^c=(\underline{\frac{7}{10}})\not \in G{\mathcal {O}}'_{F,p,q}$.

Similar to $G{\mathcal {C}}_{F,p,q}$ and $G{\mathcal {O}}_{F,p,q},$$G{\mathcal {C}}'_{F,p,q}$ need not be closed under arbitrary join and $G{\mathcal {O}}'_{F,p,q}$ need not be closed under arbitrary meet as shown in the following:

Example 3.9

Consider the dfts $(X,F,F^*)$ and ${\mathcal {F}}$ defined in Example 3.5. Then, for $p=\frac{1}{2}$ and $q=\frac{1}{4},$ we have ${\mathcal {O}}'_{F,p,q}=\left\{ \underline{0}, \underline{1}, (\underline{\frac{9}{20}})\right\}$ and

$$\begin{aligned} G{\mathcal {C}}'_{F,p,q}=&\left\{ f: \underline{0}\le f\lneq \left( \underline{\frac{2}{5}}\right) \text{ with } f(x)\lneq \frac{2}{5} {\text{ for all }} x\in X \text{ OR } \right. \\ &\left. f\le \underline{1} \text{ and } f\nleq \left( \underline{\frac{9}{20}}\right) \right\} . \end{aligned}$$

But, for the collection ${\mathcal {F}} = \left\{ f: \underline{0}\le f\lneq (\underline{\frac{2}{5}}) \text{ with } f(x)\lneq \frac{2}{5} {\text{ for all }} x\in X\right\} \subseteq G{\mathcal {C}}'_{F,p,q},$${\displaystyle \bigvee _{f\in {\mathcal {F}}}}f=(\underline{\frac{2}{5}})\not \in G{\mathcal {C}}'_{F,p,q},$ i.e., $G{\mathcal {C}}'_{F,p,q}$ is not closed under arbitrary join.

Subsequently, $G{\mathcal {O}}'_{F,p,q}$ is not closed under arbitrary meet.

Generalized fuzzy b-closed sets and generalized fuzzy b-open sets

This section identifies the algebraic structures associated with the families $b{\mathcal {C}}_{F,p,q}$ and $b{\mathcal {O}}_{F,p,q}$ of (p, q)-fbc sets and (p, q)-fbo sets, respectively.

Remark 4.1

It should be noted that ${\mathcal {C}}_{F,p,q}\subseteq b{\mathcal {C}}_{F,p,q}$ and ${\mathcal {O}}_{F,p,q}\subseteq b{\mathcal {O}}_{F,p,q}$.

In [6], it is claimed that every (p, q)-gfc set is a (p, q)-fbc set. That is, with respect to our notations, the claim is $G{\mathcal {C}}_{F,p,q}\subseteq b{\mathcal {C}}_{F,p,q}$. But this is not true as proved in the following:

Example 4.2

Consider the dfts defined in Example 3.5. For $p=\frac{1}{2},$ and $q=\frac{1}{4},$ we have seen that,

$$\begin{aligned}G{\mathcal {C}}_{F,p,q}=& \left\{ f: \underline{0}\le f\lneq \left( \underline{\frac{2}{5}}\right) \text{ with } f(x)\lneq \frac{2}{5} {\text{ for all }} x\in X \text{ OR } \right. \\ & \left. f\le \left( \underline{\frac{11}{20}}\right) \text{ and } f\nleq \left( \underline{\frac{9}{20}}\right) \text{ OR } f\le \underline{1} \text{ and } f\nleq \left( \underline{\frac{3}{4}}\right) \right\} . \end{aligned}$$

Further,

$$\begin{aligned}b{\mathcal {C}}_{F,p,q}=&\left\{ f: \underline{0}\le f\lneq \underline{1} \text{ and } f(x)\lneq \frac{9}{20} {\text{ for some }} x\in X \text{ OR }\right. \\ & \left( \underline{\frac{9}{20}}\right) \le f\le \left( \underline{\frac{11}{20}}\right) \text{ OR } \left( \underline{\frac{11}{20}}\right) \le f\lneq \underline{1} \text{ and } \\ &\left. f(x)\le \frac{3}{5} {\text{ for some }} x\in X \text{ OR } f= \underline{1}\right\} . \end{aligned}$$

Clearly, $G{\mathcal {C}}_{F,p,q}\nsubseteq b{\mathcal {C}}_{F,p,q}$ since $f\not \in b{\mathcal {C}}_{F,p,q}$ for $f\lneq \underline{1} \text{ and } (\underline{\frac{3}{4}})\lneq f$.

Thus, in general, $G{\mathcal {C}}_{F,p,q}\nsubseteq b{\mathcal {C}}_{F,p,q}$.

However,

Theorem 4.3

$({\mathcal {C}}'_{F,p,q}\cup {\mathcal {O}}'_{F,p,q})\subseteq (b{\mathcal {O}}_{F,p,q}\cap b{\mathcal {C}}_{F,p,q})$

Proof

$$\begin{aligned} f\in {\mathcal {O}}'_{F,p,q}&\Rightarrow I_{F,F^*}(C_{F,F^*}(f,p,q),p,q)=f\\&\Rightarrow \left( I_{F,F^*}\left( C_{F,F^*}(f,p,q),p,q\right) \right) \\&\quad \wedge \left( C_{F,F^*}\left( I_{F,F^*}(f,p,q),p,q\right) \right) \le f\\&\Rightarrow f\in b{\mathcal {C}}_{F,p,q}. \end{aligned}$$

Consider $f\in {\mathcal {O}}'_{F,p,q};$ then, $f^c\in {\mathcal {C}}'_{F,p,q}\subseteq {\mathcal {C}}_{F,p,q}$ . Therefore, $C_{F,F^*}(f^c,p,q)=f^c$.

Consequently, $I_{F,F^*}(C_{F,F^*}(f^c,p,q),p,q)\le f^c$ and

$$\begin{aligned}&\left( I_{F,F^*}\left( C_{F,F^*}(f^c,p,q),p,q\right) \right) \\&\quad \wedge \left( C_{F,F^*}\left( I_{F,F^*}(f^c,p,q),p,q\right) \right) \le f^c. \end{aligned}$$

Hence, $f^c\in b{\mathcal {C}}_{F,p,q}$ which implies $f\in b{\mathcal {O}}_{F,p,q},$ i.e., $f\in {\mathcal {O}}'_{F,p,q}\Rightarrow f\in b{\mathcal {O}}_{F,p,q}$. Thus, ${\mathcal {O}}'_{F,p,q}\subseteq (b{\mathcal {O}}_{F,p,q}\cap b{\mathcal {C}}_{F,p,q})$.

Similarly, ${\mathcal {C}}'_{F,p,q}\subseteq (b{\mathcal {O}}_{F,p,q}\cap b{\mathcal {C}}_{F,p,q})$. $\square$

Now, we investigate the algebraic structure of $b{\mathcal {O}}_{F,p,q}$ and $b{\mathcal {C}}_{F,p,q}$.

Theorem 4.4

$b{\mathcal {C}}_{F,p,q}$ is a meet semi-lattice.

Proof

Let $f_1,f_2$ be two (p, q)-fbc sets. Then,

$$\begin{aligned}&C_{F,F^*}\left( I_{F,F^*}(f_1\wedge f_2,p,q),p,q\right) \\&\quad =C_{F,F^*}\left( I_{F,F^*}(f_1,p,q)\wedge I_{F,F^*}(f_2,p,q),p,q\right) \\&\quad \le \left( C_{F,F^*}\left( I_{F,F^*}(f_1,p,q),p,q\right) \right) \\&\qquad \wedge \left( C_{F,F^*}\left( I_{F,F^*}(f_2,p,q),p,q\right) \right) \end{aligned}$$

Also, since $f_1\wedge f_2\le f_1$ and $f_1\wedge f_2\le f_2,$

$$\begin{aligned}&I_{F,F^*}\left( C_{F,F^*}(f_1\wedge f_2,p,q),p,q\right) \\&\quad \le \left( I_{F,F^*}\left( C_{F,F^*}(f_1,p,q),p,q\right) \right) \\&\qquad \wedge \left( I_{F,F^*}\left( C_{F,F^*}(f_2,p,q),p,q\right) \right) \end{aligned}$$

Therefore,

$$\begin{aligned}&\left( C_{F,F^*}\left( I_{F,F^*}(f_1\wedge f_2,p,q),p,q\right) \right) \\&\quad \wedge \left( I_{F,F^*}\left( C_{F,F^*}(f_1\wedge f_2,p,q),p,q\right) \right) \\&\quad \le \left( C_{F,F^*}\left( I_{F,F^*}(f_1,p,q),p,q\right) \right. \\&\qquad \left. \wedge C_{F,F^*}\left( I_{F,F^*}(f_2,p,q),p,q\right) \right) \\&\qquad \wedge \left( I_{F,F^*}\left( C_{F,F^*}(f_1,p,q),p,q\right) \right. \\&\qquad \left. \wedge I_{F,F^*}\left( C_{F,F^*}(f_2,p,q),p,q\right) \right) \\&\quad =\left[ \left( C_{F,F^*}\left( I_{F,F^*}(f_1,p,q),p,q\right) \right) \right. \\&\qquad \left. \wedge \left( I_{F,F^*}\left( C_{F,F^*}(f_1,p,q),p,q\right) \right) \right] \\&\qquad \wedge \left[ \left( C_{F,F^*}\left( I_{F,F^*}(f_2,p,q),p,q\right) \right) \right. \\&\qquad \left. \wedge \left( I_{F,F^*}\left( C_{F,F^*}(f_2,p,q),p,q\right) \right) \right] \\&\quad \le f_1\wedge f_2, \end{aligned}$$

Hence, $f_1\wedge f_2$ is a (p, q)-fbc. $\square$

Corollary 4.5

$b{\mathcal {O}}_{F,p,q}$is a join semi-lattice.

Moreover,

Theorem 4.6

$b{\mathcal {O}}_{F,p,q}$ and $b{\mathcal {C}}_{F,p,q}$ are monoids.

Proof

$\underline{0}$ is the identity in $b{\mathcal {O}}_{F,p,q},$ and $\underline{1}$ is the identity in $b{\mathcal {C}}_{F,p,q}$. The closure property follows from Theorem 4.4 and Corollary 4.5, and associativity follows from that of $I^X$. $\square$

In general, $b{\mathcal {C}}_{F,p,q}$ is not a join semi-lattice and $b{\mathcal {O}}_{F,p,q}$ is not a meet semi-lattice illustrated as follows:

Example 4.7

Let $X=I$ and consider the dfts defined in Example 3.4. Then, for $p=\frac{13}{20}$ and $q=\frac{3}{10},$ we have

$$\begin{aligned} b{\mathcal {C}}_{F,p,q} =& \left\{ f\in I^X: \underline{0}\le f\lneq \underline{1} \text{ and } f\left( \frac{11}{20}\right) <\frac{1}{3} \text{ OR } \right. \\ & f\le \left( \underline{\frac{2}{5}}\right) \text{ and } \frac{7}{20}\le f\left( \frac{11}{20}\right) \le \frac{2}{5} \text{ OR }\\ & \left( \underline{\frac{1}{3}}\right) \nleq f \text{ and } \frac{7}{20}\le f\left( \frac{11}{20}\right) \text{ OR } \\ &\left( \underline{\frac{2}{5}}\right) \le f \text{ and } \left( \underline{\frac{3}{5}}\right) \nleq f \text{ OR } \\ & \left( \underline{\frac{3}{5}}\right) \le f\le \left( \underline{\frac{2}{3}}\right) \wedge \left( \frac{11}{20}\right) _{\frac{7}{20}}^c \text{ OR } \\ & \left( \underline{\frac{2}{3}}\right) \wedge \left( \frac{11}{20}\right) _{\frac{7}{20}}^c\lneq f\lneq \underline{1} \text{ with } \left( \underline{\frac{3}{4}}\right) \nleq f \\& {\text{ and either }} f\left( \frac{11}{20}\right) \ge \frac{3}{4} \text{ or } \\ &\quad f\left( \frac{11}{20}\right) , f(x)\le \frac{3}{4} {\text{ for some }} x\ne \frac{11}{20} \text{ OR } \\ & \left.\left( \frac{11}{20}\right) _{\frac{7}{20}}^c\le f\lneq \left( \frac{11}{20}\right) ^c_{\frac{1}{4}} \text{ OR } f=\underline{1}\right\} \\ \end{aligned}$$

and $b{\mathcal {O}}_{F,p,q}=\left\{ f:f^c\in b{\mathcal {C}}_{F,p,q}\right\}$.

Clearly, $(\underline{\frac{9}{25}}),(\frac{11}{20})_{\frac{9}{20}} \in b{\mathcal {C}}_{F,p,q}$ and $(\underline{\frac{9}{25}})^c, (\frac{11}{20})_{\frac{9}{20}}^c\in b{\mathcal {O}}_{F,p,q}$. But, $(\underline{\frac{9}{25}})\vee (\frac{11}{20})_{\frac{9}{20}}\not \in b{\mathcal {C}}_{F,p,q}$.

Subsequently, $(\underline{\frac{9}{25}})^c\wedge (\frac{11}{20})_{\frac{9}{20}}^c=\left( (\underline{\frac{9}{25}})\vee (\frac{11}{20})_{\frac{9}{20}}\right) ^c\not \in b{\mathcal {O}}_{F,p,q},$

i.e., neither $b{\mathcal {C}}_{F,p,q}$ is a join semi-lattice nor $b{\mathcal {O}}_{F,p,q}$ is a meet semi-lattice.

Now, we leave the following question open:

Is $b{\mathcal {C}}_{F,p,q}$ closed under arbitrary meet?

Equivalently, Is$b{\mathcal {O}}_{F,p,q}$closed under arbitrary join?

The remaining part of this section investigates the algebraic structures associated with $Gb{\mathcal {C}}_{F,p,q}$ and $Gb{\mathcal {O}}_{F,p,q}$.

Remark 4.8

Note that for every $f\in I^X,$$bC_{F,F^*}(f, p,q)\le C_{F,F^*}(f, p,q)$.

Remark 4.9

[6] Also, note that $b{\mathcal {C}}_{F,p,q}\subseteq Gb{\mathcal {C}}_{F,p,q}$. Consequently, $b{\mathcal {O}}_{F,p,q}\subseteq Gb{\mathcal {O}}_{F,p,q}$.

Contrary to the case of $b{\mathcal {C}}_{F,p,q}$ and $b{\mathcal {O}}_{F,p,q},$$Gb{\mathcal {C}}_{F,p,q}$ and $Gb{\mathcal {O}}_{F,p,q}$ are neither a join semi-lattice nor a meet semi-lattice.

Example 4.10

Consider the dfts defined in Example 3.4 and let $p=\frac{13}{20}$ and $q=\frac{3}{10}$. Then, from Example 4.7, we have

$$\begin{aligned} b{\mathcal {C}}_{F,F^*}(f,p,q)=&\left\{ \begin{array}{ll} f, &\quad \text{ if } f\in b{\mathcal {C}}_{F,p,q}\\ f\vee \left( \frac{11}{20}\right) _{\frac{7}{20}}, &\quad \text{ if } f\nleq \left( \underline{\frac{2}{5}}\right) \text{ and } f\ngeq \left( \underline{\frac{1}{3}}\right) \text{ with } \frac{1}{3}\le f\left( \frac{11}{20}\right) \lneq \frac{7}{20}\\ &\quad \text{ OR } f \lneq \left( \underline{\frac{2}{5}}\right) \text{ with } \frac{1}{3}\le f\left( \frac{11}{20}\right) \lneq \frac{7}{20}\\ f\vee \left( \underline{\frac{2}{5}}\right) ,&\quad \text{ if } f\lneq \underline{1} \text{ with } \frac{1}{3}\le f\left( \frac{11}{20}\right) \lneq \frac{7}{20} \text{ and } \\ &\quad f(x)\ge \frac{2}{5} {\text{ for all }} x\ne \frac{11}{20} \text{ OR } f\nleq \left( \underline{\frac{2}{5}}\right) \\ &\quad \text{ and } \left( \underline{\frac{1}{3}}\right) \le f \text{ with } \frac{1}{3}\le f\left( \frac{11}{20}\right) \lneq \frac{7}{20}\\ &\quad \text{ OR } \left( \underline{\frac{1}{3}}\right) \vee \left( \frac{11}{20}\right) _\frac{7}{20} \lneq f\lneq \underline{1} \text{ with } f\nleq \left( \underline{\frac{2}{5}}\right) \\ &\quad \text{ and } f(x)\lneq \frac{2}{5} {\text{ for some }} x\in I\\ f\vee \left( \left( \underline{\frac{2}{3}}\right) \wedge \left( \frac{11}{20}\right) ^c_{\frac{7}{20}}\right) ,&\quad \text{ if } \left( \underline{\frac{3}{5}}\right) \lneq f\lneq \underline{1} \text{ with } f\nleq \left( \underline{\frac{2}{3}}\right) \wedge \left( \frac{11}{20}\right)^c_{\frac{7}{20}}\\ &\quad \text{ and } f\ngeq \left( \underline{\frac{1}{3}}\right) \wedge \left( \frac{11}{20}\right)^c_{\frac{7}{20}}\\ \left( \frac{11}{20}\right) ^c_{\frac{7}{20}}, &\quad \text{ if } \left( \underline{\frac{3}{5}}\right) \le f\lneq \left( \frac{11}{20}\right)^c _{\frac{7}{20}} \\ \left( \frac{11}{20}\right) ^c_{\alpha }, &\quad \text{ if } \left( \underline{\frac{3}{4}}\right) \wedge \left( \frac{11}{20}\right)^c _{\frac{7}{20}} \le f\lneq \left( \frac{11}{20}\right)^c_{\frac{1}{4}} \text{ with } f\left( \frac{11}{20}\right) \lneq \frac{3}{4}\\ &\quad \text{ where } \alpha = 1-f\left( \frac{11}{20}\right) \\ \underline{1},& \quad \text{ if } \left( \underline{\frac{3}{4}}\right) \le f\lneq \underline{1} \end{array}\right. \end{aligned}$$

Then, $Gb{\mathcal {C}}_{F,p,q}=\left\{ f\in I^X: f\ne (\underline{\frac{1}{3}}) \text{ or } f\ne (\underline{\frac{3}{4}}) \text{ or } f\ne (\frac{11}{20})_\frac{1}{3} \text{ or } f\ne (\frac{11}{20})_\frac{1}{4}^c\right\}$ and

$$Gb{\mathcal {O}}_{F,p,q}=\left\{ f:f^c\in Gb{\mathcal {C}}_{F,p,q}\right\} .$$

Note that there are plenty of fuzzy sets $f_1,f_2\in Gb{\mathcal {C}}_{F,p,q}$ such that $f_1\vee f_2=(\underline{\frac{1}{3}})$. But, $(\underline{\frac{1}{3}})\not \in Gb{\mathcal {C}}_{F,p,q}$. Hence, $Gb{\mathcal {C}}_{F,p,q}$ is not a join semi-lattice.

Similarly, $Gb{\mathcal {C}}_{F,p,q}$ is not a meet semi-lattice. Consequently, $Gb{\mathcal {O}}_{F,p,q}$ is not a join semi-lattice or a meet semi-lattice.

A lattice associated with a double fuzzy topological space

For a given dfts $(X,F,F^*),$ and $p\in I_0,$$q\in I_1$ with $p+q\le 1,$ take ${\mathbb {L}}_{p,q}^F=\{{\mathcal {L}}_{F,p,q}, {\mathcal {O}}_{F,p,q},{\mathcal {C}}_{F,p,q}, G{\mathcal {O}}_{F,p,q}, G{\mathcal {C}}_{F,p,q},G{\mathcal {O}}'_{F,p,q},G{\mathcal {C}}'_{F,p,q},b{\mathcal {O}}_{F,p,q}, b{\mathcal {C}}_{F,p,q}, Gb{\mathcal {O}}_{F,p,q},Gb{\mathcal {C}}_{F,p,q}, I^X\},$ where ${\mathcal {L}}_{F,p,q}$ is a De Morgan algebra as shown in [19]. Then, ${\mathbb {L}}_{p,q}^F$ is a lattice under set inclusion, whose Hasse diagram is given in the following if all the elements in ${\mathbb {L}}_{p,q}^F$ are distinct:

Examples 3.4, 3.8, 4.7 and 4.10 establish the existence of a dfts in which all the 12 elements of ${\mathbb {L}}_{p,q}^F$ are distinct.

It is easy to observe that,

Theorem 5.1

The lattice ${\mathbb {L}}_{p,q}^F$ is associative and complemented.

However,

Theorem 5.2

The lattice${\mathbb {L}}_{p,q}^F$is not distributive and hence not modular.

Proof

$Gb{\mathcal {C}}_{F,p,q}\wedge (b{\mathcal {C}}_{F,p,q}\vee Gb{\mathcal {O}}_{F,p,q})=Gb{\mathcal {C}}_{F,p,q}\ne b{\mathcal {C}}_{F,p,q}=(Gb{\mathcal {C}}_{F,p,q}\wedge b{\mathcal {C}}_{F,p,q} )\vee (Gb{\mathcal {C}}_{F,p,q}\wedge Gb{\mathcal {O}}_{F,p,q})$. $\square$

The following theorem characterizes the situation under which the lattice ${\mathbb {L}}_{p,q}^F$ contains only the greatest and the least elements:

Theorem 5.3

Let$(X,F,F^*)$be a dfts. Then,${\mathbb {L}}_{p,q}^F=\{{\mathcal {L}}_{F,p,q}, I^X\}$if and only if${\mathcal {O}}_{F,p,q}={\mathcal {C}}_{F,p,q}$.

Proof

Suppose ${\mathcal {O}}_{F,p,q}={\mathcal {C}}_{F,p,q}$. Then,

$$\begin{aligned}f\in {\mathcal {O}}_{F,p,q}&\Rightarrow f\in {\mathcal {C}}_{F,p,q}\\& \Rightarrow C_{F,F^*}(f,p,q)=f\\& \Rightarrow I_{F,F^*}(C_{F,F^*}(f,p,q),p,q)=f\\&\Rightarrow f\in {\mathcal {O}}'_{F,p,q}, \end{aligned}$$

i.e., ${\mathcal {O}}_{F,p,q}\subseteq {\mathcal {O}}'_{F,p,q}$.

Hence, ${\mathcal {C}}_{F,p,q}={\mathcal {O}}_{F,p,q}= {\mathcal {O}}'_{F,p,q},$ since ${\mathcal {O}}'_{F,p,q}\subseteq {\mathcal {O}}_{F,p,q}$ always. Therefore, $G{\mathcal {C}}_{F,p,q}=G{\mathcal {C}}'_{F,p,q}$. Consequently, $G{\mathcal {O}}_{F,p,q}=G{\mathcal {O}}'_{F,p,q}$.

For any $f\in I^X,$$f\le C_{F,F^*}(f,p,q)$. Then, $C_{F,F^*}(f,p,q)=\bigvee \{g\in {\mathcal {C}}_{F,p,q}:f\le g\}\Rightarrow C_{F,F^*}(f,p,q)=\bigvee \{g\in {\mathcal {O}}_{F,p,q}:f\le g\},$ since ${\mathcal {C}}_{F,p,q}= {\mathcal {O}}_{F,p,q}$. Hence, $\forall h\in \mathcal {O}_{F,p,q}$ with $f\le h,$$C_{F,F^*}(f,p,q)\le h,$

i.e., $G\mathcal {C}_{F,p,q}=I^X$. Consequently, $G\mathcal {O}_{F,p,q}=I^X$.

Again for any $f\in I^X,$$I_{F,F^*}(f,p,q)\le f$. But since $\mathcal {O}_{F,p,q}=\mathcal {C}_{F,p,q},$$C_{F,F^*}(I_{F,F^*}(f,p,q),p,q)=I_{F,F^*}(f,p,q)\le f$. Therefore, $f\in b\mathcal {C}_{F,p,q}$ for all $f\in I^X,$

i.e., $b\mathcal {C}_{F,p,q}=I^X$. Hence, $b\mathcal {O}_{F,p,q}=I^X$.

Conversely, suppose $\mathbb {L}_{p,q}^F=\{\mathcal {L}_{F,p,q}, I^X\}$. Then, $\mathcal {O}_{F,p,q}=\mathcal {C}_{F,p,q}=\mathcal {L}_{F,p,q}$. For, if $\mathcal {O}_{F,p,q}=I^X,$ then $\mathcal {C}_{F,p,q}=I^X$. Consequently, $\mathcal {L}_{F,p,q}=I^X$ a contradiction. $\square$

In the light of the above theorem, the following observation is obvious:

Theorem 5.4

Let$(X,F,F^*)$be a dfts such that$\mathbb {L}_{p,q}^F=\{0,1\}$for all$p\in I_0$and$q\in I_1$with$p+q\le 1$. Then, $(X,F,F^*)$is double fuzzy normal.

Let L be a finite bounded lattice. The zero-divisor graph of L is a simple graph G(L) with vertices in $Z^*(L) = Z(L)\setminus \{0\},$ the set of nonzero zero divisors of L and, for any two distinct elements a and b in $Z^*(L),$ the vertices a and b are adjacent if and only if $a \wedge b = 0$. Now, the zero divisors of $\mathbb {L}_{p,q}^F$ are $Z(\mathbb {L}_{p,q}^F)=\mathbb {L}_{p,q}^F\setminus \{I^X\}$.

Also, the zero-divisor graph $G(\mathbb {L}_{p,q}^F)$ of $\mathbb {L}_{p,q}^F$ is $K_{5,5}$ which is a five-regular complete bipartite graph as shown in the following

All the crisp sets in $\mathcal {L}_{F,p,q},$ except $\underline{1}$ are its zero divisors!

Theorem 5.5

Let $(X,F,F^*)$ be a dfts. Then,

$\left\{ \chi _A\in \mathcal {L}_{F,p,q}: A\subsetneq X\right\} \subseteq Z(\mathcal {L}_{F,p,q})$.

Proof

Since $\mathcal {L}_{F,p,q}=\mathcal {O}_{F,p,q} \cap \mathcal {C}_{F,p,q},$ for any $f\in \mathcal {L}_{F,p,q},$$f^c\in \mathcal {L}_{F,p,q}$. In particular, for $f\in \mathcal {L}_{F,p,q}\setminus \{\underline{1}\}$ such that $f=\chi _A$ for some $A\subsetneq X, \exists~ g=f^c\in \mathcal {L}_{F,p,q}, g\ne \underline{0}$ and $f\wedge g=\underline{0}$.

Hence, $\left\{ \chi _A\in \mathcal {L}_{F,p,q}: A\subsetneq X\right\} \subseteq Z(\mathcal {L}_{F,p,q})$. $\square$

Remark 5.6

From the proof of above theorem, it also follows that if $f=\chi _A\in Z(\mathcal {L}_{F,p,q}),$ then $\{h\in \mathcal {L}_{F,p,q}: h\le \chi _A\}\subseteq Z(\mathcal {L}_{F,p,q}),$ since $h\wedge f^c\le f\wedge f^c=\underline{0}$.

Theorem 5.7

Let$(X,F,F^*)$be dfts and$\mathcal {L}_{F,p,q}$be a Booleanalgebra for some$p\in I_0, q\in I_1$with$p+q\le 1$. Then,$Z(\mathcal {L}_{F,p,q})= \mathcal {L}_{F,p,q}\setminus \{\underline{1}\}$.

Proof

By Theorem 2.18, $\mathcal {L}_{F,p,q}\subseteq \left\{ \chi _A: A\subseteq X\right\}$. Also, by Theorem 5.5,

$$\begin{aligned} \left\{ \chi _A\in \mathcal {L}_{F,p,q}: A\subsetneq X\right\} \subseteq Z(\mathcal {L}_{F,p,q}). \end{aligned}$$

Moreover, by definition of the set of zero divisors of a lattice L, $Z(L)\subsetneq L$.

Hence, $Z(\mathcal {L}_{F,p,q})= \mathcal {L}_{F,p,q}\setminus \{\underline{1}\},$ by Theorem. $\square$

In [19], the authors had proved that $\mathcal {C}_{F,p,q}$ is a bounded lattice. Hence,

Theorem 5.8

A dfts$(X,F,F^*)$is (p, q)-connected iff the subgraph of$G(\mathcal {C}_{F,p,q})$induced by the vertices having the property$f\vee g=\underline{1}$is empty.

Proof

$$\begin{aligned}&(X,F,F^*)\hbox { is }(p,q)-\hbox {connected }\\&\quad \Leftrightarrow \not \exists f,g \in C_{F,p,q}\setminus \{\underline{0}\}\hbox { such that }f\vee g=\underline{1}\hbox { and }f\wedge g=\underline{0}\\&\quad \Leftrightarrow \hbox { either }f\wedge g\ne \underline{0}\hbox { or }f\vee g\ne \underline{1}\hbox { for any }f,g\in C_{F,p,q}\setminus \{\underline{0}\}.\\&\quad \Leftrightarrow \hbox { the subgraph of }G(\mathcal {C}_{F,p,q})\hbox { induced by the vertices}\\&\qquad \hbox {having the property}~ f\vee g=\underline{1}\hbox { is empty}. \end{aligned}$$

$\square$

Conclusion

For a given dfts, the algebraic structures of the families of (p, q)-gfo sets ($G\mathcal {O}_{F,p,q}$), (p, q)-gfc sets ($G\mathcal {C}_{F,p,q}$), (p, q)-rgfo sets ($G\mathcal {O}'_{F,p,q}$), (p, q)-rgfc sets ($G\mathcal {C}'_{F,p,q}$), (p, q)-fbc sets ($b\mathcal {C}_{F,p,q}$), (p, q)-fbo sets ($b\mathcal {O}_{F,p,q}$), (p, q)-gfbc sets ($Gb\mathcal {C}_{F,p,q}$) and (p, q)-gfbo ($Gb\mathcal {O}_{F,p,q}$) are investigated. The following table summarizes the results obtained:

Property	Family
	$\mathcal {L}_{F,p,q}$	$\mathcal {O}_{F,p,q}$	$\mathcal {C}_{F,p,q}$	$G\mathcal {O}_{F,p,q}$	$G\mathcal {C}_{F,p,q}$	$G\mathcal {O}'_{F,p,q}$	$G\mathcal {C}'_{F,p,q}$	$b\mathcal {O}_{F,p,q}$	$b\mathcal {C}_{F,p,q}$	$Gb\mathcal {O}_{F,p,q}$	$Gb\mathcal {C}_{F,p,q}$
Join semi-lattice	$\checkmark$	$\checkmark$	$\checkmark$	$\times$	$\checkmark$	$\times$	$\checkmark$	$\checkmark$	$\times$	$\times$	$\times$
Meet semi-lattice	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\times$	$\checkmark$	$\times$	$\times$	$\checkmark$	$\times$	$\times$
Monoid	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\times$	$\times$

Whenever these families are distinct and different from $I^X,$ together with $I^X,$ they form a bounded associative, complemented lattice, $\mathbb {L}_{p,q}^F$. Some properties of the dfts reflected in the lattice $\mathbb {L}_{p,q}^F$ and its zero-divisor graph are also brought out.