Introduction

In statistical meaning, it is known that the performance of a statistical analysis depends on the selected model distribution for a data set. If the selected distribution is an optimal model to data, then the obtained statistical inference from the dataset is the best. Because of this, a number of researchers suggested adding extra parameters to the distributions in order to be able to create more flexible distributions. Quadratic rank transmutation map (QRTM) technique is one of these methods. Depending on a base distribution, the transmuted distribution is obtained as follows.

Suppose that X is a real-valued random variable and also \(G\left( x\right) \) and \(g\left( x\right) \) are the cumulative distribution function (cdf) and the probability density function (pdf) of X, respectively. Then

$$\begin{aligned} F\left( x\right) =\left( 1+\Lambda \right) G\left( x\right) -\Lambda G\left( x\right) ^{2} \end{aligned}$$
(1)

and

$$\begin{aligned} f\left( x\right) =g\left( x\right) \left[ \left( 1+\Lambda \right) -2\Lambda G\left( x\right) \right] ,\ \ \ -1\le \Lambda \le 1 \end{aligned}$$
(2)

are called a transmuted cdf and pdf, respectively, depending on base cdf \(G\left( x\right) \) and pdf \(g\left( x\right) \), where \(\Lambda \) is the transmuting parameter [18]. So far, it has been shown by the conducted studies that the QRTM distributions obtained from the base distributions are better models to the dataset than the base distributions, because QRTM distributions have more parameters and they are more flexible than the base distribution. Khan et al. [10] proposed the Transmuted Generalized Exponential distribution using the QRTM method, and they compared their model with existing lifetime distributions such as, TGE, exponentiated Weibull (EW), modified Weibull (MW), generalized exponential (GE), weighted exponential, extended exponential (EE), Weibull (W), and Power generalized Weibull (PGW). Kemaloglu and Yilmaz [8] presented the Transmuted two-parameter Lindley distribution (TTLD) as a new lifetime distribution. They studied some important statistical properties of the TTLD. Aryal and Tsokos [2] introduced the transmuted Weibull distribution and studied its mathematical properties. In 2013, Merovci applied the QRTM to the exponentiated exponential distribution and introduced the transmuted exponentiated exponential distribution as a lifetime distribution [13]. We refer the interested reader to [3, 4, 9, 14, 16, 17, 20] and the references therein for more literature information on the transmuted families of distributions.

The main goal of this study is to create a more flexible distribution called transmuted wrapped exponential (TWE) for the modeling of circular data based on QRTM method. The QRTM technique is employed for the first time for a wrapped distribution with this study.

The rest of this paper is organized as follows: In "TWE distribution" section, the cdf and pdf of TWE distribution are obtained. In addition, some important properties of the TWE distribution such as trigonometric moments, characteristic function, location, dispersion, median, skewness, kurtosis, modality behavior, order statistics, entropy, stress-strength reliability and hazard rate function are studied in that section. The statistical inference problem for the TWE distribution according to the maximum likelihood (ML), the least squares (LS) and the weighted least squares (WLS) method are discussed in "Inference" section. A series of simulation experiments for comparing the performance of the obtained estimators are performed in "Monte Carlo simulation study" section. We analyze a real-life dataset from the literature for illustrative purposes in "Application to real data" section. Finally, the last section of the paper concludes the study.

TWE distribution

The wrapping method is a well-known approach to obtain a circular distribution based on a distribution family. The wrapped distributions play quite an important role in the modeling of circular data. Jammalamadaka and Kozubowski [5] introduced the wrapped exponential (WE) distribution with following pdf and cdf,

$$\begin{aligned} f_{X_{w}}\left( \theta \right) =\frac{\lambda {\mathrm{e}}^{-\lambda \theta }}{1-{\mathrm{e}}^{-2\pi \lambda }} \end{aligned}$$
(3)

and

$$\begin{aligned} F_{X_{w}}\left( \theta \right) =\frac{1-{\mathrm{e}}^{-\lambda \theta }}{1-{\mathrm{e}}^{-2\pi \lambda }}, \end{aligned}$$
(4)

respectively, where \(\lambda >0\) and \(\theta \in \left[ 0,2\pi \right) \). The main motivation of this study is to obtain a more flexible circular distribution than WE to the optimal modeling of circular data. Therefore, by using formulas (3) and (4) in QRTM method, we obtain cdf and pdf of a TWE distributed random variable \(\Theta \) as

$$\begin{aligned} F_{\Theta }\left( \theta \right) =\frac{\left( {\mathrm{e}}^{-\lambda \theta }-1\right) \left( c+\Lambda \left( 1+c-{\mathrm{e}}^{-\theta \lambda }\right) \right) }{c^{2}} \end{aligned}$$
(5)

and

$$\begin{aligned} f_{\Theta }\left( \theta \right) =\frac{2\lambda \Lambda {\mathrm{e}}^{-\theta \lambda }\left( {\mathrm{e}}^{-\theta \lambda }-1\right) }{c^{2}}-\frac{\lambda {\mathrm{e}}^{-\theta \lambda }\left( \Lambda +1\right) }{c}, \end{aligned}$$
(6)

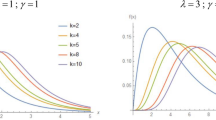
respectively, where and through the paper \(c={\mathrm{e}}^{-2\pi \lambda }-1\), \(\lambda >0\), \(\left| \Lambda \right| \le 1\) and \(\theta \in \left[ 0,2\pi \right) \). From now on, a random variable \(\Theta \) distributed the TWE with parameters \(\lambda \) and \(\Lambda \) will be indicated as \(\Theta \sim {\mathrm{TWE}}\left( \lambda ,\Lambda \right) \). Figure 1 illustrates the some of the possible shapes of the pdf of a TWE distribution for different values of the parameters \(\lambda \) and \(\Lambda \).

Fig. 1
figure 1

Pdf of transmuted wrapped exponential distribution for different values of \(\lambda \) and \(\Lambda \)

Full size image

As it can be seen from Fig. 1, the TWE distribution is a unimodal distribution. When \(\Lambda >0\), the mode of the distribution is zero; otherwise, it differs from zero for some values of the \(\lambda \), see "Modality Behavior" section. We can say that the distribution has got often the negative skewness (we say anticlockwise skewness). The parameter \(\lambda \) plays an important role in the mean and variance of the TWE distribution as a heritage of its task in the exponential distribution.

Characteristic function

The characteristic function of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution is

$$\begin{aligned} \varphi _{\Theta }(p)&=\varphi _{p}=E({\mathrm{e}}^{ip\Theta }) \end{aligned}$$
(7)
$$\begin{aligned}&=\frac{\lambda \left( \lambda +ip\right) \left( 2\Lambda +c+c\Lambda \right) \left[ \left( c+1\right) {\mathrm{e}}^{2i\pi p}-1\right] }{c^{2}\left( \lambda ^{2}+p^{2}\right) }\nonumber \\&\quad -\frac{2\lambda \Lambda \left( 2\lambda +ip\right) \left[ \left( c+1\right) ^{2}{\mathrm{e}}^{2i\pi p}-1\right] }{c^{2}\left( 4\lambda ^{2} +p^{2}\right) } \end{aligned}$$
(8)

However, since a circular random variable is periodic, \(\Theta \) and \(\Theta +2\pi \) have the same distribution, and p must be restricted to the integer values [12].

Trigonometric moments

The value of the characteristic function of the circular random variable \(\Theta \sim {\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) at an integer p is called the pth trigonometric moment. One can also write pth trigonometric moments in terms of \(\alpha _{p}\) and \(\beta _{p}\)

$$\begin{aligned} \varphi _{p}=\varphi _{\Theta }(p)=\alpha _{p}+i\beta _{p},\ \ p=0,\pm \, 1,\pm \, 2,\ldots . \end{aligned}$$

where \(\alpha _{p}\) is pth cosine moment defined as \(\alpha _{p}=E(\cos p\Theta )\) and \(\beta _{p}\) is pth sine moment defined as \(\beta _{p}=E(\sin p\Theta )\). Hence, the pth cosine moment of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution is

$$\begin{aligned} \alpha _{p}=\frac{\lambda ^{2}\left( 4c\lambda ^{2}-6p^{2}\Lambda +cp^{2} -3cp^{2}\Lambda \right) }{c\left( 4\lambda ^{2}+p^{2}\right) \left( \lambda ^{2}+p^{2}\right) } \end{aligned}$$
(9)

and pth sine moment is

$$\begin{aligned} \beta _{p}=\frac{\lambda p\left( 4\lambda ^{2}\Lambda +4c\lambda ^{2}-2\Lambda p^{2}+cp^{2}+2c\lambda ^{2}\Lambda -cp^{2}\Lambda \right) }{c\left( 4\lambda ^{2}+p^{2}\right) \left( \lambda ^{2}+p^{2}\right) }, \end{aligned}$$
(10)

where \(p=0,\pm \, 1,\pm \, 2,\ldots \).

Location, dispersion and median

The pth trigonometric moment of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) can be expressed in \(\varphi _{p}=\rho _{p}{\mathrm{e}}^{i\mu _{p}}\) where \(\mu _{p} ={\text {atan}}\left( \alpha _{p}\beta _{p}^{-1}\right) \) and \(\rho _{p}=\sqrt{\alpha _{p}^{2}+\beta _{p}^{2}}\). \(\varphi _{p}\) has a special meaning for \(p=1\). The \(\rho _{1}\) and the \(\mu _{1}\) are called angular concentration and mean direction, respectively. Here \({\text {atan}}( .) \) is quadrant inverse tangent function and defined as

$$\begin{aligned} {\text {atan}}\left( y/x\right) =\left\{ \begin{array} [c]{ll} \tan ^{-1}\left( x/y\right) , &{}\quad y>0,x\ge 0\\ \pi /2, &{}\quad y=0,x>0\\ \tan ^{-1}\left( x/y\right) +\pi , &{}\quad y<0\\ \tan ^{-1}\left( x/y\right) +2\pi , &{}\quad y\ge 0,x<0\\ {\text {undefined}}, &{}\quad y=0,x=0 \end{array} \right. . \end{aligned}$$

Mean direction of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution is

$$\begin{aligned} \mu _{1}={\text {atan}}\left( \frac{c-2\Lambda +4\lambda ^{2} \Lambda +4c\lambda ^{2}-c\Lambda +2c\lambda ^{2}\Lambda }{\lambda \left( 4c\lambda ^{2}-6\Lambda +c-3c\Lambda \right) }\right) . \end{aligned}$$
(11)

The mean direction vector gives information about the mean of the distribution as an analogy of the mean in the linear models. The length of this vector is a measure of dispersion around the mean and corresponds to the usual standard deviation or variance in linear models. The angular concentration for \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution is

$$\begin{aligned} \rho _{1}=\sqrt{\frac{\lambda ^{2}\left( 2\Lambda -c+c\Lambda \right) ^{2}+4c^{2}\lambda ^{4}}{c^{2}\left( 4\lambda ^{2}+1\right) \left( \lambda ^{2}+1\right) }.} \end{aligned}$$
(12)

For a circular model, the circular variance is calculated as \(V=1-\rho _{1}\). Hence, using the (12), the circular variance of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution is obtained as

$$\begin{aligned} V=1-\sqrt{\frac{\lambda ^{2}\left( 2\Lambda -c+c\Lambda \right) ^{2} +4c^{2}\lambda ^{4}}{c^{2}\left( 4\lambda ^{2}+1\right) \left( \lambda ^{2}+1\right) }.} \end{aligned}$$
(13)

Also, the circular standard deviation calculated as \(\sigma =\sqrt{-2\ln \rho _{1}}\) and calculated for \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution as

$$\begin{aligned} \sigma =\left[ -\ln \left( \frac{\lambda ^{2}\left( 2\Lambda -c+c\Lambda \right) ^{2}+4c^{2}\lambda ^{4}}{c^{2}\left( 4\lambda ^{2}+1\right) \left( \lambda ^{2}+1\right) }\right) \right] ^{\frac{1}{2}}. \end{aligned}$$

The quantile function of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) can be easily obtained from the solution of equation \(F\left( \theta \right) -u=0\) with respect to \(\theta \) as

$$\begin{aligned} Q\left( u\right) =-\frac{1}{\lambda }\ln \left[ \frac{2\Lambda +c-c\sqrt{2\Lambda +\Lambda ^{2}-4\Lambda u+1}+c\Lambda }{2\Lambda }\right] , \end{aligned}$$
(14)

where \(u\in \left( 0,1\right) \). Then the median direction of a circular distribution is a value M such that \(\int _{0}^{M}f_{\Theta }\left( \theta \right) {\mathrm{d}}\theta =\int _{M}^{2\pi }f_{\Theta }\left( \theta \right) {\mathrm{d}}\theta =0.5\). The median of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution is obtained from equation \(M=Q\left( 0.5\right) \) as

$$\begin{aligned} M=-\frac{1}{\lambda }\ln \left[ \frac{c\left( \Lambda +1-\sqrt{\Lambda ^{2} +1}\right) }{2\Lambda }+1\right] . \end{aligned}$$
(15)

Modality behavior

\({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) is a unimodal distribution for \(\Lambda \ne 0\). The critical value of its pdf (6) can be immediately calculated as

$$\begin{aligned} \theta _{0}=-\frac{1}{\lambda }\ln \left( \frac{2\Lambda +c+\Lambda c}{4\Lambda }\right) \in \left[ 0,2\pi \right) . \end{aligned}$$

On the other hand, for

$$\begin{aligned} f_{\Theta }^{\prime \prime }\left( \theta _{0}\right) =\frac{\lambda ^{3}\left( 2\Lambda +c+\Lambda c\right) ^{2}}{4\Lambda c^{2}}<0 \end{aligned}$$

the parameter \(\Lambda \) must be negative. Thus, the mode of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \), say \(\theta _{T}\), is

$$\begin{aligned} \theta _{T}=-\frac{1}{\lambda }\ln \left( \frac{2\Lambda +c+\Lambda c}{4\Lambda }\right) \end{aligned}$$

when \(\frac{c}{3c+2}<\Lambda <\frac{c}{\left( 2-c\right) }\) and 0 otherwise.

Skewness and kurtosis

For a circular model, the pth central cosine and sine moments are\(\ {\bar{\alpha }}_{p}=E\left[ \cos p\left( \theta -\mu _{1}\right) \right] \) and \({\bar{\beta }}_{p}=E\left[ \sin p\left( \theta -\mu _{1}\right) \right] \), respectively [12]. As a measure of asymmetry, skewness coefficient is calculated by \({\varvec{\gamma }}_{1}={\bar{\beta }}_{2}V^{-3/2}\) for a circular distribution. Hence, the skewness coefficient of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) is obtained as

$$\begin{aligned} {\varvec{\gamma }}_{1}&=-V^{-3/2}\left[ \frac{\lambda \left( \lambda \sin 2\mu _{1}-2\cos 2\mu _{1}\right) \left( 2\Lambda +c+c\Lambda \right) }{c\left( \lambda ^{2}+4\right) }\right. \\&\quad \left. -\frac{\lambda \Lambda \left( c+2\right) \left( \cos 2\mu _{1}-\lambda \sin 2\mu _{1}\right) }{c\left( \lambda ^{2}+1\right) }\right] .\nonumber \end{aligned}$$
(16)

Kurtosis of a circular distribution is \({\varvec{\gamma }}_{2}=\left( {\bar{\alpha }}_{2}-\rho _{1}^{4}\right) \left( 1-\rho _{1}\right) ^{-2}\). Therefore, kurtosis coefficient of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) is obtained as

$$\begin{aligned} {\varvec{\gamma }}_{2}&=V^{-2}\left[ \frac{\lambda ^{2}\left( 2\Lambda +2c+\Lambda c\right) +2c\left( 1-\Lambda \right) -4\Lambda }{c\left( \lambda ^{4}+5\lambda ^{2}+4\right) }\lambda \sin \left( 2\mu _{1}\right) \right. \nonumber \\&\quad +\,\frac{c\lambda \left( 1+\lambda ^{2}-3\Lambda \right) -6\lambda \Lambda }{c\left( \lambda ^{4}+5\lambda ^{2}+4\right) }\lambda \cos \left( 2\mu _{1}\right) \nonumber \\&\quad \left. -\,\frac{\left[ \left( 2\Lambda -c+\Lambda c\right) ^{2}+4\lambda ^{4}c^{2}\right] ^{2}}{c^{4}\left( 4\lambda ^{2}+1\right) ^{2}\left( \lambda ^{2}+1\right) ^{2}}\right] . \end{aligned}$$
(17)

Figure 2 represents the contour plots of circular variance (V) , skewness \(\left( \gamma _{1}\right) \) and kurtosis \(\left( \gamma _{2}\right) \) of TWE distribution.

Fig. 2
figure 2

Contour plots of circular variance (V) , skewness \(\left( \gamma _1\right) \) and kurtosis \(\left( \gamma _2\right) \) coefficient of TWE distribution

Full size image

In general, for a constant value of \(\Lambda \), it can be seen from Fig. 2 that when the \(\lambda \) increases, the circular variance decreases. However, this is not true for some negative values of \(\Lambda \). Similarly, for a constant value of \(\lambda \), when \(\Lambda \) increases, the circular variance decreases. As in the circular variance, the skewness decreases when \(\lambda \) increases. On the other hand, when \(\lambda \) increases Kurtosis increases.

Order statistics

Let \(\Theta _{1},\Theta _{2},\ldots ,\Theta _{n}\) be a random sample from \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution and let \(\Theta _{(1)} \ldots \Theta _{(n)}\), \(\left( \Theta _{(1)}< \cdots <\Theta _{(n)}\right) \), denote the order statistic for this sample. Then, the pdf of the random variable \(\Theta _{(i)}\), \(i=1,2,\ldots ,n\) is obtained as

$$\begin{aligned} f_{\Theta _{(i)}}\left( \theta \right)&=\frac{n!}{(i-1)!(n-i)!} F(\theta )^{i-1}f(\theta )(1-F(\theta ))^{n-i}\nonumber \\&=\frac{\lambda n!{\mathrm{e}}^{-\lambda \theta }\kappa ^{i-1}\left( \Lambda c-2\kappa \right) \left( {\mathrm{e}}^{-\lambda \theta }-1\right) ^{i-1}}{c^{2n} (i-1)!(n-i)!}\left( c^{2}+\kappa -\kappa {\mathrm{e}}^{-\lambda \theta }\right) ^{n-i}, \end{aligned}$$
(18)

where, \(\kappa =\Lambda +c-\Lambda {\mathrm{e}}^{-\lambda \theta }+\Lambda c\). The first order and nth order statistics can be immediately calculated from (18) as

$$\begin{aligned} f_{\Theta _{(1)}}\left( \theta \right) =\frac{\lambda n{\mathrm{e}}^{-\lambda \theta }\left( \Lambda c-2\kappa \right) }{c^{2n}}\left( c^{2}+\kappa -\kappa {\mathrm{e}}^{-\lambda \theta }\right) ^{n-1}, \end{aligned}$$

and

$$\begin{aligned} f_{\Theta _{(n)}}\left( \theta \right) =\frac{\lambda n{\mathrm{e}}^{-\lambda \theta }\left( \Lambda c-2\kappa \right) }{c^{2n}}\kappa ^{n-1}\left( {\mathrm{e}}^{-\lambda \theta }-1\right) ^{n-1}, \end{aligned}$$

respectively.

Rényi and Shannon entropy

The entropy is a measure of variation or uncertainty of a random variable. In this section, we investigate the Shannon and Rényi entropy, which are two most popular entropies, for TWE distribution. The Rényi entropy of a circular random variable with pdf \(f(\theta )\) is defined as

$$\begin{aligned} {\mathrm{RE}}_{\theta }\left( \xi \right) =\frac{1}{1-\xi }\ln \int _{0}^{2\pi }f^{\xi }(\theta ){\mathrm{d}}\theta , \end{aligned}$$

for \(\xi >0\) and \(\xi \ne 1\). Thus, Rényi entropy of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution is obtained as

$$\begin{aligned} RE_{\theta }\left( \xi \right)&=\frac{2^{\xi -1}}{\lambda (1-\xi )\xi }\,\left[ _{2}F_{1}\left( -2\xi ,-\xi ;1-2\xi ;\frac{\Lambda c+c+2\Lambda }{2\Lambda }\right) \left( \frac{c^{2}}{\lambda \Lambda }\right) ^{-\xi }\right. \\&\quad \left. -\,\left( \frac{c^{2}{\mathrm{e}}^{4\pi \lambda }}{\lambda \Lambda }\right) ^{-\xi }\,_{2}F_{1}\left( -2\xi ,-\xi ;1-2\xi ;\frac{{\mathrm{e}}^{2\pi \lambda }(\Lambda c+c+2\Lambda )}{2\Lambda }\right) \right] , \end{aligned}$$

where \(_{2}F_{1}\) denotes the hypergeometric function, see [1]. The Shannon entropy is the special case of the Rényi entropy when \(\xi \rightarrow 1\) and it is defined as \(SE_{\theta }=E\left[ -\ln f(\theta )\right] \), see [11] for definition of Shannon entropy. Immediately, Shannon entropy of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution is obtained as

$$\begin{aligned} SE_{\theta }&=\frac{1}{4\left( {\mathrm{e}}^{2\pi \lambda }-1\right) ^{2}\Lambda }\left[ \left( {\mathrm{e}}^{2\pi \lambda }(\Lambda -1)+\Lambda +1\right) ^{2}\ln \left( \frac{1-\Lambda )}{\Lambda +1}\right) \right. \\&\quad +\,2{\mathrm{e}}^{2\pi \lambda }\Lambda \left( -{\mathrm{e}}^{2\pi \lambda }(\Lambda -3)-2\left( {\mathrm{e}}^{2\pi \lambda }-\Lambda -1\right) \ln \left( \frac{{\mathrm{e}}^{2\pi \lambda } \lambda (\Lambda +1)}{{\mathrm{e}}^{2\pi \lambda }-1}\right) -3(\Lambda +1)\right) \\&\quad \left. -\,2\Lambda \left( -3{\mathrm{e}}^{2\pi \lambda }(\Lambda -1)+2\left( {\mathrm{e}}^{2\pi \lambda }(\Lambda -1)+1\right) \ln \left( -\frac{\lambda (\Lambda -1)}{{\mathrm{e}}^{2\pi \lambda }-1}\right) -\Lambda -3\right) \right] . \end{aligned}$$

Stress-strength reliability

Suppose Y represents the ‘stress’ and X represents the ‘strength’ to sustain the stress, then the stress-strength reliability is denoted by \(R=P\left( Y<X\right) \). Let \(X\sim {\mathrm{TWE}}\left( \lambda _{x},\Lambda _{x}\right) \) and \(Y\sim {\mathrm{TWE}}\left( \lambda _{y},\Lambda _{y}\right) \). Stress-strength reliability \(P\left( Y<X\right) \) is

$$\begin{aligned} R&=P\left( Y<X\right) =\int P\left( Y<X~|~X=x\right) f_{X}\left( x\right) {\mathrm{d}}x=\int f_{X}\left( x\right) F_{Y}\left( x\right) {\mathrm{d}}x\\&=\frac{1}{c_{x}^{2}c_{y}^{2}}\left[ \Lambda _{y}{\mathrm{e}}^{-2\pi \left( \lambda _{x}+2\lambda _{y}\right) }\left( \frac{{\mathrm{e}}^{2\pi \lambda _{x}}\Lambda _{x} }{\lambda _{y}}-\frac{\left( c_{x}+2\right) \Lambda _{x}+c_{x}}{\lambda _{x}+2\lambda _{y}}\right) \right. \\&\quad -\,4\pi \Lambda _{x}\left( c_{y}\left( \Lambda _{y}+1\right) +\Lambda _{y}\right) +\frac{\Lambda _{y}\left( c_{x}\left( \Lambda _{x}+1\right) \lambda _{y}-\lambda _{x}\Lambda _{x}\right) }{\lambda _{y}\left( \lambda _{x}+2\lambda _{y}\right) }\\&\quad +\,\frac{2\Lambda _{x}{\mathrm{e}}^{-2\pi \lambda _{y}}\left( {\mathrm{e}}^{2\pi \lambda _{y} }-1\right) \left( \left( c_{y}+2\right) \Lambda _{y}+c_{y}\right) }{\lambda _{x}}\\&\quad +\,\frac{{\mathrm{e}}^{-2\pi \lambda _{x}}\left( {\mathrm{e}}^{2\pi \lambda _{x}}-1\right) \left( \left( c_{x}+2\right) \Lambda _{x}+c_{x}\right) \left( c_{y}\left( \Lambda _{y}+1\right) +\Lambda _{y}\right) }{\lambda _{x}}\\&\quad \left. -\,\frac{\left( \left( c_{x}+2\right) \Lambda _{x}+c_{x}\right) \left( \left( c_{y}+2\right) \Lambda _{y}+c_{y}\right) {\mathrm{e}}^{-2\pi \left( \lambda _{x}+\lambda _{y}\right) }\left( {\mathrm{e}}^{2\pi \left( \lambda _{x} +\lambda _{y}\right) }+1\right) }{\lambda _{x}+\lambda _{y}}\right] , \end{aligned}$$

where \(c_{x}={\mathrm{e}}^{-2\pi \lambda _{x}}-1\) and \(c_{y}={\mathrm{e}}^{-2\pi \lambda _{y}}-1\). If \(\lambda _{x}=\lambda _{y}=\lambda \)

$$\begin{aligned} R=\frac{\Lambda _{x}}{6\left( {\mathrm{e}}^{2\pi \lambda }-1\right) ^{4}}\left[ \begin{array}{c} -\,6{\mathrm{e}}^{4\pi \lambda }\left( \Lambda _{y}+2\right) -\,2{\mathrm{e}}^{2\pi \lambda }\left( \Lambda _{y}+3\right) \\ +\,{\mathrm{e}}^{8\pi \lambda }\left( 24\pi \lambda +5\Lambda _{y}-15\right) +\Lambda _{y}+3\\ -\,2{\mathrm{e}}^{6\pi \lambda }\left( 3(4\pi \lambda -5)+(12\pi \lambda -1)\Lambda _{y}\right) \end{array} \right] +\frac{\left( \Lambda _{y}+3\right) }{6}. \end{aligned}$$

Hazard rate function

The hazard rate function \(h_{r}\) of \(\Theta \sim {\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) random variable is

$$\begin{aligned} h_{r}\left( \theta \right)&=\frac{f\left( \theta \right) }{1-F\left( \theta \right) }\\&=\frac{\lambda {\mathrm{e}}^{-\theta \lambda }\left( 2\Lambda +c-2\Lambda {\mathrm{e}}^{-\theta \lambda }+\Lambda c\right) }{\left( \Lambda +c-\Lambda {\mathrm{e}}^{-\theta \lambda }\right) \left( {\mathrm{e}}^{-\theta \lambda }-c-1\right) }, \end{aligned}$$

where \(\theta \in \left[ 0,2\pi \right) ,~\lambda >0\), \(\left| \Lambda \right| \le 1\) and \(c={\mathrm{e}}^{-2\pi \lambda }-1\). Critical point of the \(h_{r}\left( \theta \right) \) is

$$\begin{aligned} \theta _{h}=\frac{1}{\lambda }\ln \left[ \frac{\sqrt{-c^{2}(c+1)(\Lambda -1)^{2}\Lambda (c+\Lambda )}+2(c+1)\Lambda (c+\Lambda )}{(c+1)(c+\Lambda )((c+2)\Lambda +c)}\right] . \end{aligned}$$

The hazard rate function has bathtub shape when \(\Lambda \) is in the interval

$$\begin{aligned} \left( \frac{1}{2}\left[ -c-\sqrt{c^{2}-4\left( c+1\right) }\right] ,\frac{1}{2}\left[ -c+\sqrt{c^{2}-4\left( c+1\right) }\right] \right) . \end{aligned}$$

Here, considering that the smallest value of c is \(-1\), \(h_{r}\left( \theta \right) \) appears to be a bathtub in the positive \(\Lambda \) values providing the above condition. We present Fig. 3 which plots the hazard rate functions of the \({\mathrm{TWE}}\left( 5.48,\; 0.25\right) \) and WE\(\left( 5.48\right) \) distributions for illustrative purposes.

Fig. 3
figure 3

The plots of hazard rate functions of TWE and WE distributions

Full size image

Inference

In this section, we consider the statistical inference problem for \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \). To estimate the unknown parameters of \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \), we employ the ML, LS and WLS estimation methods commonly used in the literature.

Maximum likelihood estimation

Let \(\Theta _{1},\Theta _{2},\ldots ,\Theta _{n}\) be a random sample from \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution. From (6), the logarithmic likelihood function for the random variables \(\Theta _{i},i=1,2,\ldots ,n\) can be immediately written as

$$\begin{aligned} L\left( \lambda ,\Lambda ;\; \theta _{1},\theta _{2},\ldots ,\theta _{n}\right)&=\sum _{i=1}^{n}\ln \lambda -\sum _{i=1}^{n}\ln \left( 1-{\mathrm{e}}^{-2\pi \lambda }\right) \nonumber \\&\quad +\sum _{i=1}^{n}\ln \left( \Lambda -\frac{2\Lambda \left( {\mathrm{e}}^{-\lambda \theta _{i}}-1\right) }{{\mathrm{e}}^{-2\pi \lambda }-1}+1\right) -\sum _{i=1}^{n} \lambda \theta _{i} \end{aligned}$$
(19)

If the first derivatives of (19) with respect to parameters \(\lambda \) and \(\Lambda \) are taken and equalized them to zero, then we have the following normal equations

$$\begin{aligned} \frac{\partial L}{\partial \lambda }=\frac{n}{\lambda }+\frac{2n\pi {\mathrm{e}}^{-2\pi \lambda }}{c}+\sum _{i=1}^{n}\frac{\frac{2\Lambda \theta _{i} {\mathrm{e}}^{-\lambda \theta _{i}}}{c}-\frac{4\Lambda \pi \left( C+1\right) {\mathrm{e}}^{-\lambda \theta _{i}}}{c^{2}}}{c\left( \Lambda +1\right) -\left( 2\Lambda \left( {\mathrm{e}}^{-\lambda \theta _{i}}-1\right) \right) }-\sum _{i=1}^{n}\theta _{i}=0 \end{aligned}$$
(20)

and

$$\begin{aligned} \frac{\partial L}{\partial \Lambda }=\sum _{i=1}^{n}\frac{c-\left( 2{\mathrm{e}}^{-\lambda \theta _{i}}-2\right) }{c\left( \Lambda +1\right) -\left( 2\Lambda \left( {\mathrm{e}}^{-\lambda \theta _{i}}-1\right) \right) }=0 \end{aligned}$$
(21)

where \(c={\mathrm{e}}^{-2\pi \lambda }-1\). Hence, the ML estimates of the parameters \(\lambda \) and \(\Lambda \), say \({\hat{\lambda }}_{{\mathrm{ML}}}\) and \({\hat{\Lambda }}_{\mathrm{ML}}\), respectively, can numerically be obtained from the collective solution of (20) and (21).

Least squares estimation

To obtain the least squares estimates of the \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution, let us consider the ordered random sample \(\theta _{(1)}< \cdots <\theta _{(n)}\) from this distribution. Then, the LS estimates of the unknown parameters of the \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution, say \({\hat{\lambda }}_{LS}\), and \({\hat{\Lambda }}_{LS}\), are obtained by minimizing

$$\begin{aligned} \sum _{j=1}^{n}\left( \frac{\left( 1-{\mathrm{e}}^{-\lambda \theta _{\left( j\right) } }\right) \left( c+\Lambda \left( 1+c-{\mathrm{e}}^{-\theta _{\left( j\right) }\lambda }\right) \right) }{c^{2}}-\frac{j}{n+1}\right) ^{2}, \end{aligned}$$

with respect to \(\lambda \) and \(\Lambda \), respectively. Where \(\frac{j}{n+1}\) is the expectation of the empirical distribution function of the ordered data, see Swain et al. [19]. It is known that the LS estimates are biassed. A well-known modification of LS method is the WLS, which has a lower bias than the ordinary LS. The WLS estimates of the parameters of the \({\mathrm{TWE}}\left( \lambda ,\Lambda \right) \) distribution are obtained by minimizing

$$\begin{aligned} \sum _{j=1}^{n}\frac{\left( n+1\right) ^{2}\left( n+2\right) }{j\left( n-j+1\right) }\left[ \frac{\left( 1-{\mathrm{e}}^{-\lambda \theta _{\left( j\right) } }\right) \left( c+\Lambda \left( 1+c-{\mathrm{e}}^{-\theta _{\left( j\right) }\lambda }\right) \right) }{c^{2}}-\frac{j}{n+1}\right] ^{2}, \end{aligned}$$

with respect to \(\lambda \) and \(\Lambda \).

Monte Carlo simulation study

In this section, we perform some Monte Carlo simulation studies for illustrating and comparing estimation performances of the ML, LS and the WLS estimators obtained in the previous section. In Monte Carlo simulations, we use the values of the parameters \(\lambda =0.5,1.5\) and \(\Lambda =-\,0.75,0.75\). For the different sample of sizes \(n = 30, 50,100\) and 1000, the obtained Bias and mean squared error (MSE) values based on the 1000 times replicated simulations are displayed in Table 1.

Table 1 Bias and MSE of parameter estimations for different values of sample of sizes n and parameter \(\lambda \), when \(\Lambda =-\,0.75\).and 0.75
Full size table

As can be clearly seen from Table 1, when the sample size increases, for all values of the parameters, both Bias and MSE values decreases. This shows that the estimates are precise and accurate and hence consistent and unbiased. This is an expected result for the ML estimators, since ML estimators are asymptotically unbiased estimators. The simulation results also show that the other estimators have the same characteristics. Besides, by Table 1, we can say that the ML estimators outperform both the LS and the WLS estimators with smaller MSE values.

Application to real data

In this section, to illustrate the modeling behavior of the TWE distribution on a real-life dataset , we analyze the turtle dataset, which is a popular circular dataset. This dataset contains the orientations of 76 turtles laying their eggs [6]. We obtain the maximum likelihood estimation of the parameters \(\lambda \) and \(\Lambda \) by using the “mle” subroutine in the package ‘stats4’ (version 3.4.3) of R. Note that when applying the mle subroutine, the parameter ranges should be selected as wide as possible to avoid local maxima. We also refer the advanced readers to an R package ‘wrapped’, introduced by Nadarajah and Zhang [15], for further computation in wrapped distributions.

For the turtle dataset, the ML estimation of the parameters and the corresponding mean direction and the resultant length are obtained as given in Table 2, when the dataset is modeled by the TWE distribution.

Table 2 ML estimates for turtle data
Full size table

This dataset was recently used by Joshi and Jose [7] as an application of the wrapped Lindley \(\left( {\mathcal {WL}}\right) \) distribution. In order to make a comparison, maximized log likelihood values (L), Akaike information criterion (AIC), Kolmogorov–Smirnov with p values (KS) and Watson’s \(U^{2} \, (\hbox {W}^{2})\) statistics values for the TWE, WE and \({\mathcal {WL}}\) distributions are given in Table 3.

Table 3 Summary of fits for turtle data
Full size table

Plots of the fitted densities are shown in Fig. 4. Left panel of this figure represents the circular data plot, rose diagram and fitted pdf of the TWE, WE and \({\mathcal {WL}}\) distributions. The dashed arrow points out the sample mean resultant vector with values \(m_{1}=1.12~(\sim 64.2^{\circ })\) and resultant length \(r_{1}=0.4971\), and the solid arrow points out the mean direction vector and the resultant length of the fitted TWE distribution, which their values are given in Table 2.

Fig. 4
figure 4

Plots for turtle data. Circular data plot, fitted circular pdf and rose diagram (left), linear histogram and fitted pdf (center), empirical cdf and fitted cdf (right)

Full size image

According to Table 3, the TWE distribution has the smallest negative log-likelihood value, AIC and Watson statistics than the others. Thus, we can clearly say that the TWE distribution gives better fit than \({\mathcal {WL}}\) distribution and WE distribution. Furthermore, according to the results of the KS test given in Table 3, the goodness of fit of the \({\mathcal {WL}}\) distribution cannot be accepted at a significance level of 0.05.

Conclusion

In this article, we have introduced a new transmuted wrapped distribution named TWE distribution, for modeling the circular data. To the best of our knowledge, the transmutation of a circular distribution is a new attempt to obtain more flexible circular distribution. In the paper, the pdf and the cdf of the introduced distribution are derived and their behaviors are illustrated. Rényi and Shannon entropies of the distribution are obtained in an open form. Furthermore, explicit forms of the basic characteristics of the introduced distribution such as mean, trigonometric moments, characteristic function, quantile function and others are obtained. To estimate the unknown parameters of the introduced distribution, the maximum likelihood, the least squares and the weighted least squares estimators are obtained. By a conducted Monte Carlo simulation study, the efficiencies of these estimators are comparatively illustrated. The results of the Monte Carlo simulation show that when the sample size increases, both Bias and MSE values decrease for all estimation methods. Finally, we apply the introduced distribution to a real-life dataset named turtles dataset. Using the log-likelihood, AIC and Watson’s statistic criteria, the modeling performance of the introduced distribution is compared with wrapped exponential distribution and wrapped Lindley distribution. According to the obtained results, we can say that the TWE distribution is a better model to the turtle data than WE and \({\mathcal {WL}}\) distributions.