Hybrid Legendre functions to solve differential equations with fractional derivatives

Abstract

This paper introduces an approach based on hybrid operational matrix to obtain a numerical scheme to solve fractional differential equations. The idea is to convert the given equations into a system of equations, based on the block-pulse and Legendre polynomials. Also, we employ the Banach fixed-point theorem to analyze the problem on the Banach algebra C[0, b] for some fractional differential equations, which include many key functional differential equations that arise in linear and nonlinear analysis.

Introduction

The fractional differential equation (FDE) has received considerable interest and has constituted many applications in various scientific such as continuum and statistical mechanics [10], dynamical systems [8], and optimal control problems [2, 7, 9]. The most of FDEs cannot be solved analytically, and on the other hand, many applications of these problems motivate us to develop numerical schemes for their solutions. For this purpose, some techniques were suggested and there are some studies on the numerical method to solve FDEs, for example, see [9, 11, 12, 14, 15]. Another technique applied to solve FDE is to use the operational matrix of fractional order [2, 6, 11, 17]. In this study, we present a numerical technique to solve FDEs

$$\begin{aligned} ^{C}\!D^{\mu }g(s)= & {} F\left( s,g(s)\right) ,\quad m-1<\mu \le m,\end{aligned}$$

(1a)

$$\begin{aligned} g^{(j)}(0)=d_j,\quad j=\, & {} 0,1,\dots ,m-1, \end{aligned}$$

(1b)

where $m \in \mathbb {N}$ and $^{C}\!D^{.}$ denotes the Caputo fractional derivative [3, 14]. Our suggested method is based upon the piecewise continuous functions and Legendre polynomials, depending on the operational matrices of fractional integration. The exclusivities of hybrid functions with the operational matrix are used to convert the FDE to an algebraic equation, and then, are utilized to evaluate the upon expanding unknown function by the basis functions with unknown coefficients.

The following is an overview of this article. In Sect. 2, briefly some definitions and mathematical preliminaries of the fractional calculus have been introduced. In Sect. 3, we consider existence and uniqueness theorems of the desired FDEs. Some proper properties of the hybrid basis consisting of the block-pulse functions and Legendre polynomials, and approximation of function by these basis are presented in Sect. 4. The relevant operational matrix is obtained in Sect. 5, end of this section is devoted to applying the hybrid functions method for solving FDEs. In Sect. 6, through the provided examples, our numerical finding reported and the reliability and performance of the proposed scheme is demonstrated.

Preliminaries and basic definitions

We give a few traits concerning of fractional calculus [3, 14]. Let ${g\in L}_1[0,b]$ $\text {(space of Lebesgue integrable real functions)},$ and $\mu \in R_+=(0,\infty ),$ be a fixed number.

Definition 1

The operator $J^\mu$, defined on $L_1[0,b]$ by

$$\begin{aligned} J^{\mu }g\left( s\right) =\frac{1}{\Gamma (\mu )}\int ^s_0{{\left( s-u\right) }^{\mu -1}g\left( u\right) \mathrm {d}u}, \end{aligned}$$

for $0\le s\le b$, is denominated the Riemann–Liouville fractional integral operator of order $\mu$, where $\Gamma (.)$ denotes the Gamma function.

The operator $J^{\mu }$ transforms the space $L_1[0,b]$ into itself [14].

Definition 2

The operator $^{\mathrm{RL}}\!D^{\mu }$, defined by

$$\begin{aligned} ^{\mathrm{RL}}\!D^{\mu }g = D^{\left\lceil \mu \right\rceil } J^{\left\lceil \mu \right\rceil -\mu }g \end{aligned}$$

$(\left\lceil .\right\rceil$ denote ceiling function, $\left\lceil x \right\rceil = \mathrm{min} \left\{ z\in \mathbb Z: z\ge x \right\} )$ is called the Riemann–Liouville fractional differential operator.

Definition 3

For $g\in L_1[0,b]$,

$$\begin{aligned} ^{C}\!D^{\mu }g\left( s\right) = \left\{ \begin{array}{l} J^{m-\mu }D^mg(s),\quad m-1<\mu <m,\quad \;m\in \mathbb {N}, \\ \frac{\mathrm{d}^m}{\mathrm{d}t^m}g\left( s\right) ,\quad \mu =m, \end{array} \right. \end{aligned}$$

is the Caputo fractional derivative.

Note that $\; J^{\mu }\;^{C}\!D^{\mu }g\left( s\right) =g\left( s\right) -\sum ^{ m-1}_{ j=0}g^{\left( j\right) }\left( 0^+\right) \frac{ s^j}{ j!},\quad m-1<\mu \le m,\ \ m\in \mathbb {N}.$

Lemma 1

[3] Let $\mu \ge 0$. Assume that g is such that both $^{C}\!D^{\mu }g$ and $^{\mathrm{RL}}\!D^{\mu }g$ exist. Then,

$$\begin{aligned} ^{C}\!D^{\mu }g\left( s\right) =^{\mathrm{RL}}\!D^{\mu }g\left( s\right) - \sum ^{\left\lceil \mu \right\rceil -1}_{ j=0}\frac{D^jy(0)}{\Gamma (j-\mu +1)}s^{ j-\mu }. \end{aligned}$$

Under the hypotheses of Lemma 1, $^{C}\!D^{\mu }g\left( s\right) =^{\mathrm{RL}}\!D^{\mu }g\left( s\right)$ holds if and only if g has an $\left\lceil \mu \right\rceil$-fold zero at 0, i.e., if and only if $D^jy\left( 0\right) =0,$ for $j=0, 1, \dots , \left\lceil \mu \right\rceil -1.$

Existence and uniqueness

We study the solvability of Problem () for $g\in C[0,b]$. In what follows, we suppose that $F(s,.):[0,b]\times \mathbb R\longrightarrow {\mathbb R},$ be satisfied in the Lipschitz condition respect to the second component, with Lipschitz constant l, and there exist the constants $\lambda$ and $\eta$ such that $\left| F\left( s,g(s)\right) \right| \le \lambda +\eta \left| g(s)\right|$(sublinear nonlinearity), for all $s\in [0,b]$ and $g(s)\in {\mathbb R}$.

Theorem 1

For $0<\theta =\frac{l b^{\mu }}{\Gamma (\mu +1)} <1$, Eq. (1a) and (1b) has a unique solution.

Proof

To prove this result, we define operator $\Lambda$ on the space C[0, b] with

$$\begin{aligned} \left( \Lambda g\right) (s) =\frac{ 1}{\Gamma \left( \mu \right) }\int ^ s_0\left( s-u\right) ^{\mu -1} F \left( u,g(u)\right) \mathrm {d}u ,\quad s\in \left[ 0,b\right] . \end{aligned}$$

We shall show that $\Lambda :[0,b]\times \mathbb R\longrightarrow {\mathbb R}$ is a contraction map. For $g_1,g_2\in C[0,b]$ and $s\in [0,b]$, we have

$$\begin{aligned} \left| \left( \Lambda g_1\right) (s) -\left( \Lambda g_2\right) (s)\right|= & {} \frac{1}{\Gamma (\mu )}\left| \int ^ s_0\left( s-u\right) ^{\mu -1}\left[ F\left( u,g_1(u)\right) - F\left( u,g_2\left( u\right) \right) \right] \mathrm {d}u\right| \\\le & {} \frac{1}{\Gamma \left( \mu \right) }\int ^ s_0\left( s-u\right) ^{\mu -1} l \left[ \left| g_1\left( u\right) - g_2\left( u\right) \right| \right] \mathrm {d}u\\\le & {} \frac{1}{\Gamma \left( \mu \right) }l \left\| g_1-g_2\right\| \int ^ s_0\left( s-u\right) ^{\mu -1} \mathrm {d}u\\= & {} \frac{l s^{\mu }}{\Gamma \left( \mu +1\right) }\left\| g_1-g_2\right\| \le \theta \left\| g_1-g_2\right\| . \end{aligned}$$

Therefore, according to condition $0<\theta <1,$ the mapping $\Lambda$ is contraction, so by the Banach’s principle has a unique fixed-point, and there exists a unique solution to problem (1). $\square$

Theorem 2

$\Lambda$ maps bounded sets into equicontinuous sets of C[0, b].

Proof

Let $s_1, s_2\in [0,b],$ $s_1<s_2,$ and g belong to a bounded set, then we have

$$\begin{aligned} \left| \Lambda (g)(s_2) - \Lambda (g)(s_1)\right|\le & {} \frac{1}{\Gamma (\mu )}\left| \int ^{s_ 1}_0\left[ \left( s_2-u\right) ^{\mu -1} -(s_1-u)^{\mu -1}\right] F\left( u,g(u)\right) \mathrm {d}u\right| \\&\;\;\;\;+&\frac{1}{\Gamma (\mu )}\left| \int ^{s_ 2}_{s_ 1}(s_ 2-u) ^{\mu -1} F\left( u,g(u)\right) \mathrm {d}u\right| \\ {}\le & {} \frac{\lambda +\eta \left\| g(u)\right\| }{\Gamma (\mu )} \left| \int ^{ s_ 1}_0\left[ (s_2- u)^{\mu -1} - ( s_1-u)^{\mu -1}\right] \mathrm {d}u\right| \\&\;\;\;\;+&\frac{\lambda +\eta \left\| g(u)\right\| }{\Gamma (\mu )} \left| \int ^{s_2}_{s_1} (s_2-u)^{\mu -1} \mathrm {d}u\right| \\\le & {} 2\frac{\lambda +\eta \left\| g(u)\right\| }{\Gamma (\mu +1)}(s_ 2-s_1)^{\mu }. \end{aligned}$$

As $s_1\rightarrow s_2$ the last term tends to zero. The equicontinuous for the cases $s_1<s_2\le 0$ and $s_1\le 0\le s_2$ is explicit. $\square$

Basis functions

A set of block-pulse functions $b_p(s),p=1,2,\dots ,P$ for $s\in [0,1)$ is defined as follows [11, 12]:

$$\begin{aligned} b_p\left( s\right) = \left\{ \begin{array}{l} 1,\qquad \frac{p-1}{P}\le s<\frac{p}{ P}, \\ 0,\qquad \text {o.w.} \end{array} \right. \end{aligned}$$

(2)

These functions are disjoint and have the property of orthogonality on [0, 1).

The hybrid functions $h_{pq}(s), p=1,2,\ldots ,P,\ q=0,1,\ldots ,Q-1,$ on $[0,s_f)$ are defined as

$$\begin{aligned} h_{pq}(s)= \left\{ \begin{array}{l} L_q\left( \frac{2P}{s_f}s-2p+1\right) ,\qquad s\in \left[ \frac{p-1}{P}s_f,\frac{p}{P}s_f\right) , \\ 0,\qquad \ \text {o.w.} \end{array} \right. \end{aligned}$$

where p is the order of the block-pulse functions and $L_q(s)$s are the well-known Legendre polynomials of order q with the following recursive formula:

$$\begin{aligned} L_0(s)=1,\qquad L_1(s)=s, \end{aligned}$$

$$\begin{aligned} L_{q+1}(s)=\left( \frac{2q+1}{q+1}\right) s L_q(s) -\left( \frac{q}{q+1}\right) L_{q-1}(s),\quad q=1,2,\dots \end{aligned}$$

It is obvious that the set of hybrid functions is orthogonal. A function g(s), defined on $[0,s_f)$ can be expanded as

$$\begin{aligned} g(s)\cong \sum ^P_{p=1}\sum ^{Q-1}_{q=0}{ c_{pq}h_{pq}(s)={C_S}^\mathrm{T}H_S}(s), \end{aligned}$$

(3)

where $S=PQ$,

$$\begin{aligned} C_S=\left[ c_{10},\dots , c_{1(Q-1)}, c_{20},\dots , c_{2(Q-1)} ,\dots , c_{P0} ,\dots ,c_{P(Q-1)}\right] ^\mathrm{T}, \end{aligned}$$

and

$$\begin{aligned} H_S(s)=\left[ h_{10}(s),\dots , h_{1(Q-1)}(s), h_{20}(s),\dots , h_{2(Q-1)}(s) ,\dots , h_{P0}(s) ,\dots ,h_{P(Q-1)}(s)\right] ^\mathrm{T}. \end{aligned}$$

(4)

Applying operational matrices

Let

$$\begin{aligned} J^\mu H_S(s)\approx P^\mu _{S\times S} H_S(s), \end{aligned}$$

(5)

where $P^\mu _{S\times S}$ is obtained as the operational matrix of the fractional integration for hybrid functions, by the following formula:

$$\begin{aligned} P^\mu _{ S\times S} =\Phi _{S\times S}F_{S\times S}^\mu \Phi ^{-1}_{S\times S}. \end{aligned}$$

(6)

Also, matrix $\Phi _{S\times S}$ is an invertible matrix and define using vector $H_{S}(s)$ in collocation points $s_p =\frac{2p-1}{2S},\ p=1,2,\dots ,S$ as following:

$$\begin{aligned} \Phi _{S\times S} =\left[ H_{S}\left( \frac{1}{2S}\right) \ \ H_{S}\left( \frac{3}{2S}\right) \ \dots \ H_{S}\left( \frac{2S-1}{2S}\right) \right] , \end{aligned}$$

and

$$\begin{aligned} F_{S\times S}^\mu =\frac{ 1}{ S^\mu }\frac{ 1}{\Gamma (\mu +2)}\left[ \begin{array}{llllll} 1 &{} \varepsilon _1 &{} \varepsilon _2 &{} \ldots &{} \varepsilon _{S-1} \\ 0 &{} 1 &{} \varepsilon _1 &{}\ldots &{} \varepsilon _{S-2} \\ 0 &{} 0 &{} 1&{} \ldots &{} \varepsilon _{S-3} \\ &{} \vdots &{} &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{}1 \\ \end{array} \right] , \end{aligned}$$

with $\varepsilon _j=(j+1)^{\mu +1} - 2j^{\mu +1}+(j-1)^{\mu +1},$ for $j=1,2,\ldots ,S-1$.

Furthermore, using Eq. (2) and taking $B_{S}(s)=[b_1(s),b_2(s),\ldots ,b_S(s)]^\mathrm{T},$ hybrid functions can be expanded by S-term of the block-pulse functions as

$$\begin{aligned} H_S(s)= \Phi _{S\times S}B_S(s), \end{aligned}$$

(7)

and since $F_{S\times S}^\mu$ is the operational matrix associated with the block-pulse functions, we get

$$\begin{aligned} J^\mu B_S(s)\approx F_{S\times S}^\mu B_S(s). \end{aligned}$$

(8)

Finally, from Eqs. (6)–(8), one can conclude that

$$\begin{aligned} J^\mu H_S(s)=J^\mu \Phi _ {S\times S}B _S\left( s\right) =\Phi _{ S\times S} J^\mu B _S(s) \approx \Phi _{S\times S} F_{S\times S}^\mu B _ S (s)= P^\mu _{ S\times S}\Phi _{S\times S}B_S(s). \end{aligned}$$

(9)

Method implementation

Consider a nonlinear differential equation of fractional order. We approximate $^{C}\!D^{\mu }g(s)$ by the hybrid functions as

$$\begin{aligned} ^{C}\!D^{\mu }g(s) \approx {C_S}^\mathrm{T} H_S(s), \end{aligned}$$

(10)

where $C_S=\left[ c_1,c_2,\dots ,c_{S}\right] ^\mathrm{T}$ is an unknown vector. From Eq. (10), we get

$$\begin{aligned} J^\mu \;^{C}\!D^{\mu }g(s)\approx {C_S}^\mathrm{T} J^\mu H_S(s)\Longrightarrow g(s)\approx {C_S}^\mathrm{T} J^\mu H_S(s)+\sum ^{m-1}_{j=0}\frac{d_j}{j!}s^{j}, \end{aligned}$$

from Eq. (9), we have

$$\begin{aligned} g(s)\approx {C_S}^\mathrm{T} P^\mu _{ S\times S}\Phi _{S\times S}B_S(s)+\sum ^{m-1}_{j=0}\frac{d_j}{j!}s^{j}. \end{aligned}$$

(11)

Substituting $^{C}\!D^{\mu }g(s)$ and g(s) from relations (10), (11) in Eq. (1a) and (1b), we obtain a system of algebraic equations. Implementation of the proposed method is presented in the next section via numerical experiments.

Numerical experiments

We present some examples to comprehend overview and demonstrate the efficiency of the described method.

Example 1

Consider the following FDE [1]:

$$\begin{aligned} ^{C}\!D^{0.5} g(s) =-g(s)+h(s) \end{aligned}$$

(12)

with $g(0)=0$, where $h(s)=s^2+\frac{2}{\Gamma (2.5)}s^{1.5}$ and the exact solution is $g(s)=s^2$. To solve Eq. (12), let $^{C}\!D^{0.5}g(s)={C_S}^\mathrm{T} H_{S}(s)$, using Eqs. (3), (11), we have

$$\begin{aligned} g(s)={C_S}^\mathrm{T}P^{0.5}_{S\times S}\Phi _{S\times S} B_{S}(s), \end{aligned}$$

$$\begin{aligned} h(s)=h^\mathrm{T}_{S}H_{S}(s), \end{aligned}$$

where $h^\mathrm{T}_{S}$ is a known constant vector.

Substituting these equations into Eq. (12), we give

$$\begin{aligned} {C_S}^\mathrm{T}\Phi _{{S}\times {S}}B_{S}(s)+{C_S}^\mathrm{T}P^{0.5}_{{S}\times {S}}\Phi _{{S}\times {S}}B_{S}(s)-h^\mathrm{T}_{S}\Phi _{{S}\times {S}}B_{S}(s)=0. \end{aligned}$$

(13)

We solved the problem, applying the technique described in Sect. 4, the absolute errors for $Q=3, P=2,4,6$ are listed in Table 1.

From Table 1, observed that, we have an acceptable approximation of the exact solution. Also, increasing the number of basis functions, provide improvement in the accuracy of the solutions.

Table 1 Absolute errors with $Q=3, P=2,4,6$ in different values of s for Eq. (12)

Example 2

In [4, 16, 17], the FDE

$$\begin{aligned} \left\{ \begin{array}{c} ^{C}\!D^{\mu }g\left( s\right) =-g\left( s\right) ,\quad 0<\mu \le 2, \\ g(0)=1,\quad \;\; g'(0)=0, \end{array} \right. \end{aligned}$$

(14)

has been solved by different methods. The exact solution is as follows [4]:

$$\begin{aligned} g(s)=E_{\mu }(-s^{\mu }), \end{aligned}$$

where

$$\begin{aligned} E_{\mu }(x)=\sum ^{\infty }_{j=0}\frac{x^j}{\Gamma (\mu j+1)}, \end{aligned}$$

is the Mittag–Leffler function of order $\mu$.

Since $J^{\mu }\;^{C}\!D^{\mu }g(s)=g(s)-g(0)-tg'(0),$ we have the following algebraic system for Eq. (14):

$$\begin{aligned} {C_S}^\mathrm{T}\Phi _{S\times S}B_S(s) +{C_S}^\mathrm{T} P^{\mu }_{S\times S}\Phi _{S\times S}B_S( s)-[1,1,\dots ,1]B_S(s)=0. \end{aligned}$$

For $\mu =1$ and $\mu =2$, the exact solutions of Eq. (14) are $g(s)=\mathrm{e}^{-s}$ and $g(s)= \cos s$, respectively. Figure 1 displays the numerical results for g(s) with $S=12$, $\mu = 0.25, 0.5, 0.75, 0.95,1;$ and $\mu = 1, 1.25, 1.5, 1.75, 1.95, 2$. It is evident that as $\mu$ approaches close to 1 or 2, the numerical solution by the presented hybrid method in previous sections converges to the exact solution.

Table 2 shows the absolute errors for $\mu = 0.85, 1.2, 1.5$ and $S= 8, 10, 24$. Clearly, the approximations achieved through the hybrid scheme are in accordance with those established with other mentioned numerical schemes [16, 17].

Fig. 1

Numerical solutions of Example 2, for $S =12,$ $0<\mu \le 1$ (left) and $1\le \mu \le 2$ (right)

Table 2 Absolute errors of solution Example 2, with comparison to Refs. [16, 17] for $\mu = 0.85, 1.2, 1.5$ and $S= 8, 10, 24$ in different values of s

Example 3

Consider the following fractional Riccati equation [1, 13, 18]:

$$\begin{aligned} ^{C}\!D^{\mu }g(s)=2 g(s)-g^2(s)+1,\;\;\;\;g(0)=0, \;\;\;\; 0<\mu \ \le 1. \end{aligned}$$

(15)

Assume $^{C}\!D^{\mu }g(s)= {C_S}^TH_S(s)$, using Eq. (11), we have

$$\begin{aligned} g(s)={C_S}^\mathrm{T}P^{\mu }_{S\times S}\Phi _{S\times S}B_S(s). \end{aligned}$$

Let

$$\begin{aligned} {C_S}^\mathrm{T}P^{\mu }_{S\times S}\Phi _{S\times S} =[a_1, a_2, \dots , a_S], \end{aligned}$$

applying virtues of the block-pulse function, we get

$$\begin{aligned} g^2(s)=[a^2_1, a^2_2, \dots , a^2_S]B_S(s)= A_S^\mathrm{T}B_S(s). \end{aligned}$$

Substituting these equations into FDE (15), we have the following system of nonlinear equations:

$$\begin{aligned} {C_S}^\mathrm{T}\Phi _{S\times S}B_S (s)-2 {C_S}^\mathrm{T} P^{\mu }_{S \times S}\Phi _{S\times S}B _S(s)+A_S^\mathrm{T}B_S (s)-\left[ 1,1,\dots ,1\right] B _S(s)=0. \end{aligned}$$

For $\mu =1$, the analytic solution of Eq. (15) is

$$\begin{aligned} g(s)=1+\sqrt{2}\tanh \left( \sqrt{2}s+\frac{1}{2}\ln \left( \frac{\sqrt{2}-1}{\sqrt{2}+1}\right) \right) . \end{aligned}$$

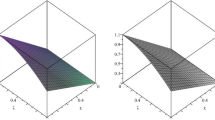
In Table 3, the results for Example 3 with $\mu = 0.5, 1$ and $S= 16,$ by the hybrid method in some points $s\in [0,1],$ are given. Also, these outcomes are compared with Refs. [13, 18]. Moreover, absolute errors of approximate solutions of Example 3 for $S=48$ are shown in Fig. 2.

Table 3 The results of Example 3 compared with Refs. [13, 18] for $S= 16$

Fig. 2

Absolute errors of Example 3 for $S=48$

Example 4

[5] We implement the presented hybrid method in this study for solving nonlinear FDE

$$\begin{aligned} \left\{ \begin{array}{c} ^{C}\!D^{1.5}g(s)+\frac{1}{10}g^3(s) = 4 \sqrt{\frac{s}{\pi }} +\frac{1}{10}s^6,\ \ \ \ 0<s\ <2, \\ g(0)=g'(0)=0,\ \end{array} \right. \end{aligned}$$

(16)

with the exact solution $g(s)=s^2$. The behavior of the results with $S=4,8,12$ is plotted in Fig. 3.

Fig. 3

Comparison of g(s) for $S=4, 8, 12$ with exact solution of Example 4

Example 5

For FDE [4, 17],

$$\begin{aligned} \left\{ \begin{array}{l} ^{C}\!D^{\mu }g(s)=\frac{40320}{\Gamma (9-\mu )}s^{8-\mu }-3\frac{\Gamma \left( 5+\frac{\mu }{2}\right) }{\Gamma \left( 5-\frac{\mu }{2}\right) }s^{4-\frac{\mu }{2}} +\frac{9}{4}\Gamma \left( \mu +1\right) +(\frac{3}{2} s^{ \mu /2}-s^4)^3- g^{\frac{3}{2}}(s), \\ 0<\mu <2, \ \ \ g(0)=0,\ \ \ g'(0)=0,\ \\ g(s)=s^8-3s^{4+\frac{\mu }{2}}+\frac{9}{4}s^\mu \; \text {(exact solution)}, \ \end{array} \right. \end{aligned}$$

the absolute errors for $\mu =0.2,0.4,\ldots ,1.8$ and $S=4$ reported in Table 4.

Table 4 Absolute error of Example 5 with $S=4$

Example 6

Finally, consider the multi-order FDE

$$\begin{aligned} \left\{ \begin{array}{lll} &{}&{}^{C}\!D^{2.5}g(s)-2\;^{C}\!D^{\frac{2}{3}}g(s)+g^{\,2}(s)=f(s),\\ &{}&{}f(s)=\cos ^2s+\frac{9}{2\;\Gamma \left(\frac{1}{3}\right)}s^{4/3}\; {_1F_2}\left(1;\frac{7}{6},\frac{5}{3}; -\frac{s^2}{4}\right)+0.752253\; s^{1.5}\; {_1F_2}(1;1.75,1.25; -\frac{s^2}{4}), \end{array} \right. \end{aligned}$$

(17)

with the exact solution $g(s)=\cos s$ and nonlocal boundary value conditions

$$\begin{aligned} \left\{ \begin{array}{cl} &{}g(0)=1,\quad g'(0)=0,\\ &{}g(0)-0.65g\left( \frac{\pi }{4}\right) =g(1), \end{array} \right. \end{aligned}$$

(18)

where ${_pF_q}(\mu _1,\mu _2,\dots ,\mu _p;\nu _1,\nu _2,\dots ,\nu _q;s)$ denotes the generalized hypergeometric function. Applying our proposed approach with Eqs. (11), (18), we have [12],

$$\begin{aligned}&^{C}\!D^{2.5}g(s)= {C_S}^\mathrm{T} H_{S}(s),\;\;^{C}\!D^{\frac{2}{3}}g(s)={C_S}^\mathrm{T}P^{\frac{11}{6}}_{S\times S}\Phi _{S\times S}B_S(s)+d_2s,\\&g(s)= {C_S}^\mathrm{T}P^{2.5}_{S\times S}\Phi _{S\times S}B_S(s)+1+\frac{d_2}{2}s^{2}, \end{aligned}$$

therefore,

$$\begin{aligned}&\nonumber g(1)= {C_S}^\mathrm{T}P^{2.5}_{S\times S}\Phi _{S\times S}B_S(1)+1+\frac{d_2}{2},\\&g\left( \frac{\pi }{4}\right) ={C_S}^\mathrm{T}P^{2.5}_{S\times S}\Phi _{S\times S}B_S\left( \frac{\pi }{4}\right) +1+d_2\frac{{{\pi }^2}}{32} .\end{aligned}$$

(19)

From boundary condition (18) and Eq. (19), one concludes that

$$\begin{aligned} d_2=-\frac{{C_S}^\mathrm{T} P^{2.5}_{S\times S}\Phi _{S\times S}B_S(1)+0.65{C_S}^\mathrm{T}P^{2.5}_{S\times S}\Phi _{S\times S}B_S\left( \frac{\pi }{4}\right) +0.65}{2\left( 1+0.65\frac{\pi ^2}{16}\right) }. \end{aligned}$$

(20)

Consequently, FDE (17) can be shown as the following algebraic system:

$$\begin{aligned}&{C_S}^\mathrm{T}\Phi _{S\times S}B_S(s)-2{C_S}^\mathrm{T}P^{\frac{11}{6}}_{S\times S}\Phi _{S\times S}B_S(s)+{A_S}^\mathrm{T} B_S(s)+2{C_S}^\mathrm{T}P^{2.5}_{S\times S}\Phi _{S\times S}B_S(s)\nonumber \\ {}&+\,d_2 s^2{C_S}^\mathrm{T}P^{2.5}_{S\times S}\Phi _{S\times S}B_S(s) =h(s), \end{aligned}$$

(21)

where ${A_S}^\mathrm{T}=[a^2_1, a^2_2, \dots , a^2_S]$, with

$$\begin{aligned} {C_S}^\mathrm{T}P^{2.5}_{S\times S}\Phi _{S\times S} =[a_1, a_2, \dots , a_S], \end{aligned}$$

and

$$\begin{aligned} h(s)=2d_2s-1-\frac{d_2^2}{4}s^4-d_2s^2+f(s). \end{aligned}$$

Using the hybrid method with $Q=5, P=5,10,20$ for $s\in (0,1)$, the maximum absolute errors of Example 6 are reported in Table 5. Also, the approximate error of our proposed scheme for this example is illustrated in Fig. 4.

Table 5 Maximum absolute errors of Example 6 with $S=25, 50, 100$

Fig. 4

Absolute error of Eq. (17) with $S=75$