Abstract
The nonlinear partial differential equation of Harry Dym is generalized by replacing the first-order time derivative by a fractional derivative of order \(\alpha ,\; 0 \le \alpha \le 2\). The aim of the present paper is to obtain an approximate solution of time fractional generalized Harry Dym equation using Adomian Decomposition Method (ADM). The fractional derivative is described in the Caputo sense. Numerical examples are given to show the application of the present technique. The results show that the solution of ADM is in good agreement with the exact solution when \(\alpha =1\), also reveal that the method is very simple and effective.
Similar content being viewed by others
Introduction
Nonlinear partial differential equations appear in many branches of physics, engineering and applied mathematics. In recent years, there has been a growing interest in the field of fractional calculus. Oldham and Spanier [1], Miller and Ross [2] and Podlubny [3] provide the history and a comprehensive treatment of this subject. Fractional calculus is the field of mathematical analysis, which deals with the investigation and applications of integrals and derivatives of arbitrary order, which can be real or complex. The idea appeared in a letter by Leibniz to L’Hospital in (1695). The subject of fractional calculus have gained importance during the past three decades and popularity, mainly due to its demonstrated applications in different areas of physics and engineering. Several fields of applications of fractional differentiation and fractional integration are already well established, some others have just started. Many applications of fractional calculus can be found in turbulence and fluid dynamics, stochastic dynamical systems, plasma physics and controlled thermonuclear fusion, nonlinear control theory, image processing, nonlinear biological systems; for more details see [4] and the references therein. Indeed, it provides several potentially useful tools for solving differential equations. The most important advantage of using fractional differential equations is their nonlocal property. It is known [5] that the integer order differential operator is nonlocal. This means that the next state of a system depends not only upon its current state but also upon all of its historical states. Hence, the importance of investigating fractional equations arises from the necessity to sharpen the concepts of equilibrium, stability states, and time evolution in the long time limit. There have been few attempts to solve linear problems with multiple fractional derivatives. In [6], an approximate solution based on the decomposition method is given for the generalized fractional diffusion-wave equation. Not much work has been done for nonlinear problems, and only a few numerical schemes have been proposed to solve nonlinear fractional differential equations. More recently, applications have included classes of nonlinear equations with multi-order fractional derivative, and this motivates us to develop a numerical scheme for their solutions.
The main objective of the present paper is to use the Adomian decomposition method [7, 8] to calculate the approximate solutions of the Dym equation that is named for Harry Dym and occurs in the study of Solitons. The Dym equation first appeared in Kruskal [9] and is attributed to an unpublished paper by Harry Dym. Harry Dym is a completely integrable nonlinear evolution equation that may be solved by means of the inverse scattering transform. It is interesting because it obeys an infinite number of conservation laws and it does not possess the Painleve property. The Dym equation has strong links to the Korteweg–de Vries equation. As mentioned in [10], the Harry Dym has been recently generalized in different ways. The authors in [11] introduced and investigated the coupled Harry Dym equations, and showed that these equations are concerned with the new iso-spectral flows. Different generalizations of the Harry Dym equation have been constructed in [12]. In [13] group analysis of time fractional Harry Dym equation was performed and some group invariant solutions are obtained. An efficient approach based on Homotopy perturbation method and Sumudu transform were proposed in [14] to solve fractional Harry Dym equation for \(0 \le \alpha \le 1\). Beside these generalizations, we would like to present a new generalization of the nonlinear partial differential equation of Harry Dym by replacing the first-order time derivative by a fractional derivative of order \(\alpha ,\; 0 \le \alpha \le 2\), and takes the form
where \(\alpha \) is a parameter describing the order of the fractional derivative, \(x\) and \(t\) are the space and time variables, and \(u(x,t)\) is the field defined in the space domain \((-\infty , \infty )\). Theoretically, \(\alpha \) can be any positive number. Note that for \(\alpha =1\), Eq. (1.1) represents the standard Harry Dym equation, which has exact solution (see, [5]) \(u(x,t)=\Big (a-\frac{3\sqrt{b}}{2}(x+ct)\Big )^{2/3}\), where \(a\), \(b\) and \(c\) are suitable constants. This type of equation has been investigated by several authors. In [5], an approximate analytical solution of time fractional Harry Dym equation is obtained using Homotopy perturbation method only for \(0 \le \alpha \le 1\). Explicit solutions for Harry Dym equation was obtained by Fuchssteinert et al. [12]. Soliton solutions of the \(2+1\) dimensional Harry Dym equation was found by Halim in [17].
The plan of this work is the following. A brief review of the fractional calculus theory is given in Sect. 2. In Sect. 3, we use the decomposition method to construct our numerical solutions for Eq. (1.1). The general response expression contains a parameter describing the order of the fractional derivative that can be varied to obtain various responses. In Sect. 4, we present some numerical results (Graphs and Tables) to show the nature of the solution as the fractional derivative parameter is changed.
Basic definition of fractional calculus
This section is devoted to a description of the operational properties of the purpose of acquainting with sufficient fractional calculus theory, to enable us to follow the solution of the generalized Harry Dym equation. Many definitions and studies of fractional calculus have been proposed in the last two centuries. These definitions include, Riemman–Liouville, Weyl, Reize, Campos, Caputa, and Nishimoto fractional operator. Mainly, in this paper, we will re-introduce section 2 of [6]. The Riemann–Liouville definition of fractional derivative operator \(J_{a}^{\alpha }\) is defined as follows:
Definition 2.1
Let \(\alpha \in \hbox{I}\!\hbox{R}_{+}\). The operator \(J^{\alpha }\), defined on the usual Lebesque space \(L_{1}[a,b]\) by
for \(a \le x \le b\), is called the Riemann–Liouville fractional integral operator of order \(\alpha \).
Properties of the operator \(J^{\alpha }\) can be found in [1], we mention the following: for \(f\in L_{1}[a,b], \alpha , \beta \ge 0\) and \(\gamma >-1\)
-
1.
\(J_{a}^{\alpha } f(x)\) exists for almost every \(x\in [a,b]\).
-
2.
\(J_{a}^{\alpha }J_{a}^{\beta } f(x)=J_{a}^{\alpha +\beta }f(x)\)
-
3.
\(J_{a}^{\alpha } J_{a}^{\beta } f(x)=J_{a}^{\beta } J_{a}^{\alpha } f(x)\)
-
4.
\(J_{a}^{\alpha } x^{\gamma }=\frac{\Gamma (\gamma +1)}{\Gamma (\alpha +\gamma +1)}(x-a)^{\alpha +\gamma }\).
The Riemann–Liouville derivative has certain disadvantages when trying to model real-world phenomena with fractional differential equations. Therefore, we shall introduce now a modified fractional differentiation operator \(D^{\alpha }\) proposed by Caputo in his work on the theory of visco-elasticity [19].
Definition 2.2
The fractional derivative of \(f(x)\) in the Caputo sense is defined as
\(m-1<\alpha \le m, \quad m \in \hbox{I}\!\hbox{N},\quad x>0\)
Also, we need here two of its basic properties.
Lemma 2.1
If \(m-1<\alpha \le m\) , and \( f\in L_{1}[a,b]\) , then \(D_{a}^{\alpha } J_{a}^{\alpha }f(x)=f(x)\) , and
The fractional derivative is considered in the Caputo sense. To solve differential equations, we need to specify additional conditions to produce a unique solution. For the case of Caputo fractional differential equations, these additional conditions are just the traditional conditions, which are taken to those of classical differential equations, and are, therefore, familiar to us. In contrast, for Riemann–Liouville fractional differential equations, these additional conditions constitute certain fractional derivatives of the unknown solution at the initial point \(x=0\), which are functions of \(x\). The unknown function \(u=u(x,t)\) is assumed to be a causal function of time, i.e., vanishing for \(t<0\). Also, the initial conditions are not physical; furthermore, it is not clear how much quantities are to be measured from experiment, say, so that they can be appropriately assigned in an analysis. For more details on the geometric and physical interpretation for fractional derivatives of both Riemann–Liouville and Caputo types see [18].
Definition 2.3
For \(m\) to be the smallest integer that exceeds \(\alpha \), the Caputo fractional derivatives of order \(\alpha >0\) is defined as
For mathematical properties of fractional derivatives and integrals, one can consult the above-mentioned references.
Analysis of the method
To illustrate the basic idea of the ADM for fractional Harry Dym equation, in an operator form, Eq. (1.1) can be written as
where the fractional differential operator \(D_{t}^{\alpha }\) is defined as \(D_{t}^{\alpha }=\frac{\partial ^{\alpha }}{\partial t^{\alpha }}\), so that \(D_{t}^{\alpha }\) is the operator defined in (2.1). In this study, we shall consider Eq. (1.1) subject to the initial conditions
To solve the nonlinear fractional Eq. (1.1), we apply the operator \(J^{\alpha }\), the inverse of the operator \(D_{t}^{\alpha }\), on both sides of Eq. (3.1) and using the initial condition (3.2) yields
where \(\phi (u)=u^3 u_{xxx}\). Following Adomian [7, 8], we expect the decomposition of the solution into a sum of components to be defined by the decomposition series
where the components \(u_{n}(x,t)\) will be determined recursively. The nonlinear function \(\phi (u)\) is then written in the decomposed form
where \(A_{n}\) are called the Adomian polynomials, these polynomials can be calculated for all forms of nonlinearity according to specific algorithms constructed by Adomian [7, 8]. In this specific nonlinearity, we use the general form of formula for \(A_{n}\) polynomials as
This formula is easy to set computer code to get as many polynomials as we need in the calculation of the numerical solution as well as explicit solutions. To be easy to follow by the reader, we can give the first few Adomian polynomials for \(\phi (u)=u^3 u_{xxx}\) of the nonlinearity as
and so on, the rest of the polynomials can be constructed in a similar manner. Wazwaz, in [21] developed an alternative approach for the construction of these polynomials. Substituting (3.4) and (3.5) into both sides of Eq. (3.3) gives
Following the decomposition method, we introduce the recursive relations as
and the recurrence relation given as in (3.10) determines the exact solutions, while the truncated series
give an approximate solution to the nonlinear fractional Harry Dym equation. Moreover, the decomposition series solutions (3.11) generally converge very rapidly in real physical problems. The convergence of the decomposition series have been investigated by several authors [15, 16].
Numerical applications and results
In this section, we present some numerical results to demonstrate the behavior of the solution as the order of the time fractional derivative is changed. We shall illustrate the numerical scheme by two cases. The first case is somewhat artificial in the sense that the exact answer, for the special case \(\alpha =1\), is known in advance, and the initial condition is directly taken from this answer. Nonetheless, such an approach is needed to evaluate the accuracy of the numerical scheme, and to examine the effect of varying the order of the time fractional derivative on the behavior of the solution. To calculate the terms of the decomposition series (3.11) for \(u(x,t)\), we shall mention that a second initial condition \(u_{t}(x,0)=g(x)\), for \(1 < \alpha \le 2\) is assumed to ensure continuous dependence of the solution on the parameter \(\alpha \) in the transition from \(\alpha =1^-\) to \(\alpha =1^+\). Therefore, in (3.9), we need to distinguish two cases:
-
1.
Case I: For \(0<\alpha \le 1\), in this case, we choose \(m=1\) in (3.9), and so upon using Mathematica, the solution can be obtained as
and so on, in this manner the other components of the decomposition series can easily be obtained. Substituting \(u_{0}, u_{1}, u_{2}, u_{3},\ldots\) into Eq. (3.3) gives the solution \(u(x,t)\) in a series form solution by
So, the approximate solution for the Harry Dym equation (when \(\alpha =1\) and \(n=4\)) is given by
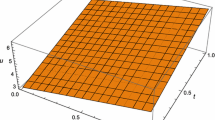
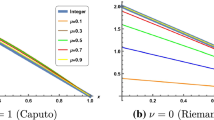
Figure 1, shows, respectively, the approximate and exact solution to this case when \(\alpha = 1\). Figure 2, shows the obtained error compared with the exact. Figure 3, shows profile solutions when \(t=1\) for different values of \(\alpha \), i.e. \(\alpha = 0.1,\ 0.2,\ 0.4,\ 0.9,\ 1\).
It can be seen from Fig. 1 that the solution obtained by the present method is nearly identical to the exact. Also, Fig. 1 shows the exact solution \(u(x,t)\) of the regular Harry Dym equation (\(\alpha = 1\)) given by Mokhtari [20] for constants value of \(a=4,\ b=1,\ c=1\).
It is known that using ADM, the series solution converges very rapidly. The rapid convergence means only few terms are required to get analytical function. From Fig. 1, it is to be noted that only four terms of the decomposition series were used for our approximations. It is evident that the solution can be improved by adding more terms of the decomposition series.
Figures 3 and 5, show that the solution propagates and diffuses with time, which means that the solution continuously depends on the fractional derivatives.
-
2.
Case II: For \(1<\alpha \le 2\), in this case, we choose \(m=2\) in (3.9) and the components are determined by
Accordingly, the approximate solution for the Harry Dym equation (when \(\alpha =2\) and \(n=4\)) is given by
Figure 4, shows the obtained approximate solution to this case when \(\alpha = 2\). Figure 5, shows profile solutions when \(t=1\) for different values of \(\alpha \), i.e. \(\alpha = 1.1,\ 1.2,\ 1.4,\ 1.9,\ 2\).
Conclusions
In this paper, the application of Adomian decomposition method was extended to explicit and numerical solution of time fractional nonlinear PDEs in mathematical physics with initial conditions. It may be concluded that the decomposition methodology is a very powerful and efficient technique that provides more realistic solutions. It also provides series solutions which generally converge very rapidly in real physical problems. The decomposition method, which is proved to be efficient in solving differential equations, can be applied to various types of fractional differential equations [6]. Finally, the recent appearance of nonlinear fractional partial differential equations as adequate models in science and engineering makes it necessary to investigate the method of solutions for such equations.
References
Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic Press, New York (1974)
Miller, K.S., Ross, B.: An introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley and Sons Inc., New York (1993)
Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1999)
Gepreel, K.: Adomian decomposition method to find approximate solutions for the fractional PDEs. WSEAS Trans. Math. 11(7), 652–657 (2012)
Kumar, S., Tripathi, M.P., Singh, O.P.: A fractional model of Harry Dym equation and its approximate solution. Ain Shams Eng. J. 4, 111–115 (2013)
Al-Khaled, K., Momani, S.: An approximate solution for a fractional diffusion wave equation using the decomposition method. Appl. Math. Comput. 165(2), 473–483 (2005)
Adomian, G.: A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 135, 501–544 (1988)
Adomian, G.: Solving Frontier Problems of Physics. The Decomposition Method. Kluwer Academic Publishers, Boston (1994)
Kruskal, M.D., Moster, J.: Dynamical systems, theory and applications. Lecturer notes physics. Springer, Berlin (1975)
Popowicz, Z.: The generalized Harry Dym equation. Phy. Lett. A 317, 260–264 (2003)
Antonowicz, M., Fordy, A.P.: Coupled Harry Dym equations with multi-Hamiltonian structures. J. Phys. A Math. Gen. 21(5), L269–L75 (1988)
Fuchssteinert, B., Schulzet, T., Carllot, S.: Explicit solutions for Harry Dym equation. J. Phys. Math. Gen. 25, 223–230 (1992)
Huang, Q., Zhdanov, R.: Symmetries and exact solutions of the time fractional Harry-Dym equation with Riemann–Liouville derivative. Phys. A 409, 110–118 (2014)
Kumar, D., Singh, J., Kilicman, A.: An efficient approach for fractional Harry Dym equation by using Sumudu transform. Abstr. Appl. Anal. 2013, 1–8. Art. ID 608943 (2013)
Cherrualt, Y.: Convergence of Adomian’s method. Kybernetes 18, 31–38 (1989)
Cherrualt, Y., Adomian, G.: Decomposition methods: a new proof of convergence. Math. Comput. Model. 18, 103–106 (1993)
Halim, A.A.: Soliton solutions of \((2+1)\) dimensional Harry Dym equation via Darboux transformation. Chaos. Soliton Fractals 36, 646–653 (2008)
Podlubny, I.: Geometric and physical interpretation of fractional integration and fractional differentiation. Fractals Calc. Appl. Anal. 5, 367–386 (2002)
Caputo, M.: Linear models of dissipation whose \(Q\) is almost frequency independent-II. Geophys. J. R. Astron. Soc. 13(5), 529–539 (1967)
Mokhtari, R.: Exact solutions of the Harry Dym equation. Commun. Theor. Phys. 55, 204–208 (2011)
Wazwaz, A.M.: A new algorithm for calculating Adomian polynomials for nonlinear operators. Appl. Math. Comput. 111, 53–69 (2000)
Author information
Authors and Affiliations
Corresponding author
Additional information
An erratum to this article is available at http://dx.doi.org/10.1007/s40096-015-0154-9.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Al-Khaled, K., Alquran, M. An approximate solution for a fractional model of generalized Harry Dym equation. Math Sci 8, 125–130 (2014). https://doi.org/10.1007/s40096-015-0137-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40096-015-0137-x