Skip to main content
SpringerLink
Log in

Terahertz emission during laser-plasma interaction: effect of electron temperature and collisions

  • Research
  • Published:
Journal of Theoretical and Applied Physics

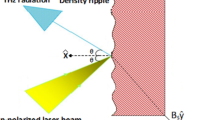
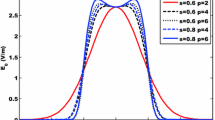
Abstract

The electron-neutral collisions in the plasma become crucial with regard to the generation of THz radiation when thermal motion of the electrons is considerable. If we look at the mechanism of THz emission, this is only the movement/oscillations of the electrons which is responsible for the excitation of nonlinear current that generated the THz radiation. The present work aims to disclose the role of thermal motion of the plasma electrons to the resonance condition and the THz emission when two co-propagating super-Gaussian laser beams beat in the plasma. The dynamics of the plasma electrons and subsequent generation of nonlinear current are discussed in greater detail for the emission of THz radiation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Jung, C.: International seminar on advanced accelerator and radiation physics. Synchrotron Radiat. News 29, 11–13 (2016)

    Article  Google Scholar 

  2. Li, X.F., Yu, Q., Gu, Y.J., Qu, J.F., Ma, Y.Y., Kong, Q., Kawata, S.: Calculating the radiation characteristics of accelerated electrons in laser-plasma interactions. Phys. Plasmas 23(3), 033113 (2016)

    Article  ADS  Google Scholar 

  3. Starodubtsev, M., Krafft, C., Lundin, B., Thévenet, P.: Resonant Cherenkov emission of whistlers by a modulated electron beam. Phys. Plasmas 6(7), 2862–2869 (1999)

    Article  ADS  Google Scholar 

  4. Lemos, N., Martins, J.L., Tsung, F.S., Shaw, J.L., Marsh, K.A., Albert, F., Joshi, C.: Self-modulated laser wakefield accelerators as x-ray sources. Plasma Phys. Control. Fusion 58(3), 034018 (2016)

    Article  ADS  Google Scholar 

  5. Demir, P., Kacar, E., Akman, E., Bilikmen, S.K., Demir, A.: Theoretical and experimental investigation of soft x-rays emitted from TIN plasmas for lithographic application. In Ultrafast X-Ray Sources and Detectors (Vol. 6703, p. 67030B). International Society for Optics and Photonics (2007)

  6. Dorranian, D., Ghoranneviss, M., Starodubtsev, M., Ito, H., Yugami, N., Nishida, Y.: Generation of short pulse radiation from magnetized wake in gas-jet plasma and laser interaction. Phys. Lett. A 331(1–2), 77–83 (2004)

    Article  ADS  Google Scholar 

  7. Dorranian, D., Ghoranneviss, M., Starodubtsev, M., Yugami, N., Nishida, Y.: Microwave emission from TW-100 fs laser irradiation of gas jet. Laser Part. Beams 23(4), 583–596 (2004)

    Article  ADS  Google Scholar 

  8. Manouchehrizadeh, M., Dorranian, D.: Effect of obliqueness of external magnetic field on the characteristics of magnetized plasma wakefield. J. Theor. Appl. Phys. 7(1), 43 (2013)

    Article  ADS  Google Scholar 

  9. Starodubtsev, M., Kamal-Al-Hassan, M., Ito, H., Yugami, N., Nishida, Y.: Low-frequency sheath instability stimulated by an energetic ion component. Phys. Plasmas 13(1), 012103 (2006)

    Article  ADS  Google Scholar 

  10. Malik, A.K., Malik, H.K., Nishida, Y.: Terahertz radiation generation by beating of two spatial-Gaussian lasers. Phys. Lett. A 375(8), 1191–1194 (2011)

    Article  ADS  Google Scholar 

  11. Mun, J., Park, S., Yea, K.: Relationship between Terahertz and X-ray signals generated from laser-induced plasma on gas targets. J. Korean Phys. Soc. 56(11), 275–278 (2010)

    Article  ADS  Google Scholar 

  12. Singh, D., Malik, H.K.: Enhancement of terahertz emission in magnetized collisional plasma. Plasma Sources Sci. Technol. 24(4), 045001 (2015)

    Article  ADS  Google Scholar 

  13. Malik, A.K., Malik, H.K., Kawata, S.: Investigations on terahertz radiation generated by two superposed femtosecond laser pulses. J. Appl. Phys. 107(11), 113105 (2010)

    Article  ADS  Google Scholar 

  14. Wang, W.M., Sheng, Z.M., Wu, H.C., Chen, M., Li, C., Zhang, J., Mima, K.: Strong terahertz pulse generation by chirped laser pulses in tenuous gases. Opt. Express 16(21), 16999–17006 (2008)

    Article  ADS  Google Scholar 

  15. Wang, W.M., Kawata, S., Sheng, Z.M., Li, Y.T., Zhang, J.: Towards gigawatt terahertz emission by few-cycle laser pulses. Phys. Plasmas 18(7), 073108 (2011)

    Article  ADS  Google Scholar 

  16. Malik, L., Escarguel, A.: Role of the temporal profile of femtosecond lasers of two different colours in holography. EPL (Europhys. Lett.) 124(6), 64002 (2019)

    Article  Google Scholar 

  17. Malik, L.: Dark hollow lasers may be better candidates for holography. Opt. Laser Technol. 132, 106485 (2020)

    Article  Google Scholar 

  18. Ostermayr, T., Petrovics, S., Iqbal, K., Klier, C., Ruhl, H., Nakajima, K., Li, R.: Laser plasma accelerator driven by a super-Gaussian pulse. J. Plasma Phys. 78(4), 447–453 (2012)

    Article  ADS  Google Scholar 

  19. Devi, L., Malik, H.K.: Resonant third harmonic generation of super-Gaussian laser beam in a rippled density plasma. J. Theor. Appl. Phys. 12(4), 265–270 (2018)

    Article  ADS  Google Scholar 

  20. Singh, D., Malik, H.K.: Terahertz generation by mixing of two super-Gaussian laser beams in collisional plasma. Phys. Plasmas 21(8), 083105 (2014)

    Article  ADS  Google Scholar 

  21. Hung, T.S., Ho, Y.C., Chang, Y.L., Wong, S.J., Chu, H.H., Lin, J.Y., Chen, S.Y.: Programmably structured plasma waveguide for development of table-top photon and particle sources. Phys. Plasmas 19(6), 063109 (2012)

    Article  ADS  Google Scholar 

  22. Sheng, Z.M., Zhang, J., Umstadter, D.: Plasma density gratings induced by intersecting laser pulses in underdense plasmas. Appl. Phys. B 77(6–7), 673–680 (2003)

    Article  ADS  Google Scholar 

  23. Kim, K.Y., Taylor, A.J., Glownia, J.H., Rodriguez, G.: Coherent control of terahertz supercontinuum generation in ultrafast laser–gas interactions. Nat. Photon. 2(10), 605–609 (2008)

    Article  Google Scholar 

  24. Kuo, C.C., Pai, C.H., Lin, M.W., Lee, K.H., Lin, J.Y., Wang, J., Chen, S.Y.: Enhancement of relativistic harmonic generation by an optically preformed periodic plasma waveguide. Phys. Rev. Lett. 98(3), 033901 (2007)

    Article  ADS  Google Scholar 

  25. Malik, H.K.: Density bunch formation by microwave in a plasma-filled cylindrical waveguide. EPL (Europhys. Lett.) 106(5), 55002 (2014)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Plasma Waves and Particle Acceleration (PWAPA) Laboratory, Department of Physics, Indian Institute of Technology, Delhi, New Delhi, 110 016, India

    Hitendra K. Malik

  2. Rajdhani College, Delhi University, Delhi, New Delhi, India

    Divya Singh

Authors
  1. Hitendra K. Malik
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Divya Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hitendra K. Malik.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Malik, H.K., Singh, D. Terahertz emission during laser-plasma interaction: effect of electron temperature and collisions. J Theor Appl Phys 14, 359–365 (2020). https://doi.org/10.1007/s40094-020-00392-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40094-020-00392-3

Keywords

Search

Navigation