Investigation of physical issues of the initial conditions of free water surface due to underwater disturbances on the basis of SPH numerical simulation of the phenomenon

Abstract

The current paper discusses the physical impacts of the various initial boundary conditions of the free surface of a waterbody on the initiation and propagation characteristics of water waves due to the underwater perturbations. Differences between traditional point of view and applied numerical method in this paper for exertion the initial conditions of the generated waves by surface deformation were surveyed in the Lagrangian domain vs. Eulerian. In this article, the smoothed-particle hydrodynamics (SPH) technique was applied for simulating of wave generation process using initial boundary condition of water surface deformation through utilizing DualSPHysics numerical code and comparing the modeling results with recorded data. As a distinct approach, we studied the effects of discrete water particles on properties of produced surface waves by using the Lagrangian analytical capability of SPH model. Illustrative compatibility on simulation results with experimental data proves that meshless techniques such as applied in DualSPHysics software can reproduce physical properties of the event very well, and this is a suitable alternative to existing classical approaches for prediction of shock occurrences with nonlinear behavior such as generated surface water waves by underwater disturbance. Besides, the waveforms and their characteristics behave more realistic by considering the thrown upward water mass which was not directly considered in old formula and theories. The results of numerical modeling indicated rational agreement between numerical and empirical data proving that a complicated nonlinear phenomenon could be predicted by an SPH model which modified initial boundary conditions were supposed into the model with actual assumptions.

Introduction and previous studies

Explosive behavior is the consequence of an internal chemical conversion which abandons massive amounts of heat and gas in a short term. Energy content of a normal explosive material is less than those evolved by combustion of an equal mass of any fuel, but due to the shorter time of combustion for explosive materials releases much greater rate of energy. On the other hand, underwater disturbances generate relatively slow, outward-moving surface waves. Such waves are originated by upward movement of explosion-induced gas bubble which is bursting on the surface.

After an underwater disturbance, a shock wave reaches the water surface and lifts it at an initial velocity of $V_{0}$ which depends on depth of loading. The further expansion of bubble displaces water and creates a dome at the water surface. Due to the explosion changes, the outer surface of dome and forms a semi-cylindrical water column with a wall thickness that is lower than the top of column. Finally, the wall becomes very thin and breaks, and then the vapor and gas will release into the atmosphere; this concept has been studied by Kozachenko and Khristoforov [1, 2].

Previous studies on underwater explosion phenomena studied different related fields such as field measurement, laboratory tests, analytical solutions, and numerical simulation. In this regard, some researchers focused on the bubble behavior during its movement, while others studied the stages of bubble collapse and wave creation through different methods and hypotheses. Herring [3] introduced the system of equations describing an evolution of bubble explosion, and this study has been reviewed and addressed by following researchers [2, 4,5,6].

Penney and Price [7] focused on the stability of an initially spherical bubble rising under the buoyancy forces. Charlesworth [8] performed a series of tests and studied underwater explosion effects on wave generation and propagation. Penney [9] introduced an analytical relationship for dome and crater formation during bubble collapse near free water surface. Besides, he also worked on gravity water waves caused by explosions. Bryant [10] applied Penney’s analytical solution for test results. Kaplan and Goodale [11] modeled detailed characteristics of explosion cavities at lower pressure on a small-scale test. LeMehaute [12] developed a generalization of the Cauchy–Poisson’s theory [13] to a finite disturbance of arbitrary form. VanDorn [14,15,16] and Whalin [17, 18] introduced applications of Kranzer and Keller’s analytical approach [19]. A theory was developed to predict the wave properties at the target travel time and distance for source energy, displacement and travel path depth profile by Jordaan [20, 21]. Several studies are performed about propagation of water waves due to disturbances, and a sort of concepts are raised such as VanDorn et al. [14,15,16]. Amsden [22]; Hirt and Rivard [23], Hirt [24], Fogel, et al. [25] and Mader [26,27,28,29] introduced a theoretical mathematical model for simulation of hydrodynamics related to underwater explosion and subsequent bubble dynamics and free surface effects. Bottin and outlaw [30] and Bottin [31] conducted field studies on disturbance which generated waves on shallow water. Le Mehaute et al. [32,33,34], Wang, et al. [35, 36] and Khangaonkar and Le Mehaute [37] numerically determined the initial conditions for a target experimental wave record at a defined distance from zero surface are by reverse transforms. Le Mehaute and Le Mehaute and Khangaonkar [33] proposed a simple relationship for horizontal radius of cavity when it was developed at a defined shallow water depth. Wang [38, 39] simulated crater formation and surface movement.

The present paper considered the initial conditions of generated water wave by the underwater disturbance based on the analytical models as well as a new approach for simulation of wave generation and propagation. Results of these numerical models are compared with field and laboratory measurements to evaluate their performance. SPH method was the applied numerical model in these studies.

The present study aimed to investigate the precision of SPH-type methods for measuring generated water waves by underwater disturbance occurrence; hence, some new modeling tested cases were compared with proposed analytical solutions in the literature, experimental data as well as traditional numerical modeling results. Finally, the results of applied method in this article are compared with previous methods.

Underwater explosion mechanism

Bubble pulsation

Effects of an underwater explosion depend on several parameters including distance from explosion source, explosion energy, depth of disturbance, and water depth. When an underwater explosion occurs, the submerged detonation almost instantaneously produces a hot gas or plasma with small volume. High temperatures and pressures may cause two types of disturbances in ambient fluid:

• (a) Release of a shock wave moves from center of bubble toward a semi-infinite medium.

• (b) Radial motion of fluid particles in a way that the generated bubble including fume and explosive residues is expanded.

Figure 1 shows the evolution of various features of an underwater explosion and a wide variety of phenomena at different depths.

Fig. 1

Surface effects at underwater explosions, and schemes of their expansion based on experimental data (reported by Kedrinskii, 1988)

According to Fig. 1, the underwater explosions obviously generate multiple forms of phenomena that are complex and not easy to understand.

Therefore, most studies were conducted on dynamics of bubble evolution and migration of both conventional and nuclear test cases by Cole [40], Snay [41, 42], Holt [43], Falade and Holt [44], Li and Holt [45]. Later, small scale and limited experiences in the laboratory were fulfilled, and also various types of numerical codes were developed and applied for study on underwater disturbance phenomena. In the case that there is a large explosion depth of burst, the bubble begins to rise due to its buoyancy. During the expansion phase, the pressure within the bubble considerably falls below the ambient hydrostatic pressure due to the obtained outward momentum by water. The motion then reverses and the bubble contracts under hydrostatic overladen pressure acquiring inward momentum and adiabatically compressing the central gas volume to a lower pressure. Upon reaching its minimum diameter, energy is radiated by the emission of a second shock wave, and the bubble expands again (LeMehaute and Wang 1998). A variety of phenomena are observed if the bubble survives to reach the free surface. Depending upon the depth of burst, these phenomena may include a well-formed hollow column, a chaotic splash, and development of a prominent base surge. This “initial” turbulence may have quite great duration extending from the first appearance of a mound as the bubble is nearing the free surface, to completion of upward water fall (LeMehaute 1971).

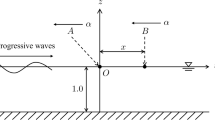
In the case of near-surface disturbance, the nature of the created surface motion and magnitude of water waves depend upon form of bubble when it reaches the surface. Depending upon the burst depth, this may include a well-formed hollow column, a very high and narrow jet or a low turbulent mound followed by development of a prominent “base surge.” Cole (1948) presented images of the apparent free surface effects and plumes as a function of burst depth. Some other tests indicate that the initial solitary wave is among the characteristics of explosions in shallow water. Detonations in deep water generate a train of waves where numbers of crests and troughs increase as the train propagates outward from center of disturbance. Properties of dispersive wave motion in the space–time field were derived for general conditions and certain practical applications. Maximum wave heights, periods, lengths, velocities, travel times, envelopes, group velocities, and modification by a shoaling bottom can be uniquely expressed in terms of initiating disturbance as stated by VanDorn (1961), LeMehaute (1991–1992), Whalin (1965) and Jordaan (1965–1966).

In the case of deep water or near-surface explosions with low yield quantity after reaching bubble to the free water surface region, sea surface started deformation into a dome-shaped body (see Fig. 2). During this process, water layer at the top of water becomes thinner and unstable until its strength is broken; hence, the confined gas and vapor inside the bubble will be released outward. Finally, the fragmented bubble will be reshaped into a crater which is surrounded by its around lip shape (see Fig. 3).

Fig. 2

Rising dome due to expansion and upward migration of bubble (presented by LeMehaute 1992)

Fig. 3

Generating crater and lips after bubble collapse (presented by LeMehaute 1992)

Initial conditions of free surface

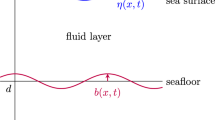
In this type of problems, an underwater generated bubble by an explosion is considered when it reaches a place very close to the free surface in its latest part of migration toward the water surface. Obviously, it has a large internal pressure relative to the atmospheric pressure. It will rise toward the water level and burst suddenly. Once the bubble collapses, this is often accompanied by a jet shooting up from the bottom of the bubble. When the thrown water particles loss their kinetic energy and attain to the possible maximum height, they will fall back due to the gravity. During this sort of events, the free surface of water starts to oscillate due to primary and secondary disturbances that are generated by surface deformation and impact of fallen water particles, respectively. Consequently, a second peak or more may appear before water-free surface major deformation decreases progressively via wave propagation toward the far field, (Kedrinskii [46] and Ni et al. [47]).

To simulate the surface waves generated by the underwater explosion, these perturbations are applied to the free surface of the water in the form of initial boundary conditions. The previous studies found that there were multiple choices of initial conditions (including initial surface deformation, initial surface velocity, initial surface pressure and various combinations of these cases) in order to simulate the wave generation mechanism for a definite disturbance. However, the present report studied the underwater explosions primarily because the converted energy to water waves is significantly larger for air explosions. It is well established that the use of a surface deformation as an initial condition results in a wave train which is qualitatively similar to those measured in explosions, (LeMéhauté and Wang [48]).

Most types of free surface deformations were studied and applied for simulation and prediction of primary water wave generation due to the underwater explosion (see Figs. 4, 5, and 6). The most applied initial functions are presented by Whalin [18, 49] and LeMehaute [12, 48] as follows:

$$\eta_{0} \left( {r_{0} } \right) = \left\{ {\begin{array}{ll} {\eta_{0} \left[ {1 - \left( {\frac{{r_{0} }}{R}} \right)^{2} } \right]; } & {r_{0} \le R} \\ {0; } & {r_{0} > R} \\ \end{array} } \right.$$

(1)

$$\eta_{0} \left( {r_{0} } \right) = \left\{ {\begin{array}{ll} {\eta_{0} \left[ {1 - 2\left( {\frac{{r_{0} }}{R}} \right)^{2} } \right]; } & {r_{0} \le R} \\ {0;} & {r_{0} > R} \\ \end{array} } \right.$$

(2)

$$\eta_{0} \left( {r_{0} } \right) = \left\{ {\begin{array}{ll} {\eta_{0} \left[ {\frac{1}{3}\left( {\frac{{r_{0} }}{R}} \right)^{4} - \frac{4}{3}\left( {\frac{{r_{0} }}{R}} \right)^{2} + 1} \right] ;} & {r_{0} \le \sqrt 3 R} \\ {0 ;} & {r_{0} > \sqrt 3 R} \\ \end{array} } \right.$$

(3)

The law of conservation of mass is ignored in the quadratic deformation without the lip (see Fig. 4), but other formulas tried to observe the law. In the second form, an uncommon discontinuity is produced in the geometry of water surface by the outer face of lip area in the vicinity of water-free surface line. Therefore, the initial water deformation of quadratic model is approximately smooth, but discontinuity on the outer edge of lip is mild in comparison with quadratic models.

Fig. 4

Initial quadratic deformation without lip around the crater on the basis of Eq. 1 (presented by Whalin 1967)

Fig. 5

Initial quadratic deformation with lip around the crater on the basis of Eq. 2 (presented by Whalin 1967)

Fig. 6

Initial quadratic deformation with lip around the crater on the basis of Eq. 3 (presented by Whalin 1967)

A variety of studies are conducted on various mathematical and numerical analyses by direct or reverse methodologies to find the best relationship between experimental data series and analytical solutions. Results are sometimes incompatible with real-time measurements, but a good fit is sometimes gained. Incredibly, some scientists obtained better results using without-lip quadratic formation which had discontinuity in geometry and could not comply with mass conservation law (Whalin [49]).

Therefore, the initial conditions which are commonly used for predicting water waves generated by underwater explosions consist of one of the stationary surface deformations above according to considerable studies. The present research studied the same hypotheses for water-free line initial deformation and compared them with other hypotheses.

Energy in explosion waves

Efficiency of an explosion as a wave producing mechanism is one of the important issues. This section estimated the potential energy of three surface deformations in order to predict water waves. This subject is related to field measurements of the maximum envelope at various stations with a distance “r” from center of explosion at water-free level (surface zero). Further theoretical studies and curves are also presented to show a relationship between potential and kinetic energy in the wave train at the time t after the detonation.

If the initial stationary water surface deformation is considered as $\eta_{0} \left( {r_{0} } \right)$, the potential energy of primary wave can be calculated according to equation by Whalin [17, 18, 49]:

$$E = 2\pi \rho g \mathop \smallint \limits_{0}^{\infty } \frac{{\eta_{0}^{2} \left( {r_{0} } \right)}}{2}r_{0} {\text{d}}r_{0}$$

(4)

Amount of energy can be measured according to equations by Whalin for different types of initial water surface deformation:

$${\text{Quadratic}}\;{\text{surface}}\;{\text{deformation}}\;{\text{without lip}}: E = \frac{{\pi \rho g\eta_{0}^{2} R^{2} }}{6}$$

(5)

$${\text{Quadratic}}\;{\text{surface}}\;{\text{deformation}}\;{\text{with}}\;{\text{lip}}: E = \frac{{\pi \rho g\eta_{0}^{2} R^{2} }}{6}$$

(6)

$${\text{Quartic}}\;{\text{surface}}\;{\text{deformation}}\;{\text{with}}\;{\text{lip}}:E = \frac{{\pi \rho g\eta_{0}^{2} R^{2} }}{5}$$

(7)

Based on the previous studies on the underwater explosion, it is proven that the total explosion energy is approximately divided into three parts as:

• 1. 40% in the pulsating motion of bubble,

• 2. 30% wasted irreversibly in water heating, and

• 3. 30% is radiated as a nonreturning pressure pulse. It is also found that the kinetic energy applied to bubble pulsation phenomenon causes water wave generation (Whalin, [49]; LeMehaute, [12, 48]), and then 40% of total released explosion energy can be equated with water wave energy.

Accepting the above-mentioned issues, detonation of various charge weights $W$ lb of explosion may be measured by the following method. Imagine a spherical hole of radius h for creation in an infinite extent of sea, when the top of sphere is just at the same level as the surface of sea, the applied work for displacing water against hydrostatic plus atmospheric pressure is calculated as follows:

$$W = 4\pi \rho gh^{3} \frac{{\left( {h + z} \right)}}{3}$$

(8)

where $z$ is the head of water that produces atmospheric pressure, and $\rho$ is the water density of water. Equate this work to 40% of $E$ as the chemical energy of explosion. Thus:

$$W = E = 0.40 E_{\text{explosion}}$$

(9)

Description of SPH numerical model

SPH is a Lagrangian method in which the continuous medium can be discretized into a set of disordered points [50]. SPH allows any function to be expressed in terms of its values at a set of particles by interpolation without application of any grid to calculate spatial derivatives. In this way, the physical properties of each particle such as acceleration and density are quantified as an interpolation of the same values in neighbor nodes. The main feature of SPH technique is to estimate a scalar function of $A\left( \varvec{r} \right)$ at any point with r vector of position as follows:

$$A\left( \varvec{r} \right) = \smallint A\left( {{\mathbf{r}}'} \right) W\left( {\varvec{r} - \varvec{r^{\prime}},h} \right){\text{d}}\varvec{r}'$$

(10)

in Eq. (10), $h$ is called the smoothing length to present effects of the nearest particles in a neighboring domain as shown in Fig. 7; hence, it is weighted in accordance with distance between particles. Kernel function $W\left( {\varvec{r} - \varvec{r^{\prime}},h} \right)$ is used to estimate the amount of participation by smoothing length parameter.

Fig. 7

Effected area and neighbor particles of ith particle

Equation (2) is as follows in a discrete form:

$$\langle A\left( {\varvec{r}_{a} } \right)\rangle \approx \mathop \sum \limits_{b} \left( {\frac{{m_{b} }}{{\rho_{b} }}} \right)A\left( {\varvec{r}_{b} } \right) W\left( {\varvec{r}_{a} - \varvec{r}_{b} ,h} \right)$$

(11)

In Eq. (11), the summation is extended to all particles within the neighboring distance of particle “a,” and the volume associated with particle “b” is $\frac{{m_{\text{b}} }}{{\rho_{\text{b}} }}$, and thus $m_{\text{b}}$ and $\rho_{\text{b}}$ are the mass and the density of this neighbor particle, respectively. Kernel functions should have several properties including positivity inside the interaction area, compact support, normalization, and monotonic decrease with distance. A kernel option is the Wendland’s quintic kernel [51] for which the weighting function vanishes for inter-particle distances greater than $2h$. It is defined as follows by Altomare et al. [52, 53]:

$$W\left( q \right) = \alpha_{\text{D}} \left( {1 - \frac{q}{2}} \right)^{4} \left( {2q + 1} \right) ; 0 \le q \le 2$$

(12)

In Eq. (12), $q = \frac{r}{h}$ is defined as ratio of particle distance to smoothing length and $\alpha_{\text{D}}$ is a normalization constant which is equal to $\frac{7}{{4\pi h^{2} }}$ in two dimensions and $\frac{21}{{16\pi h^{3} }}$ in three dimensions.

Laws of conservation of continuum fluid dynamics in the forms of differential equations are transformed into their particles by use of kernel functions. The proposed momentum equation by Monaghan [54] is used to determine the acceleration of particle “a” as the result of particle interaction with its neighbors like particle “b”:

$$\frac{{{\text{d}}\varvec{v}_{a} }}{{{\text{d}}t}} = - \mathop \sum \limits_{b} m_{b} \left( {\frac{{P_{b} }}{{\rho_{b}^{2} }} + \frac{{P_{a} }}{{\rho_{a}^{2} }} + \varPi_{ab} } \right)\nabla_{a} W_{ab} + \varvec{g}$$

(13)

where $\varvec{v}$ is particle velocity, $P$ is particle pressure, $\varvec{g}$ is gravitational acceleration vector which is equal to $\left( {0,0, - 9.81} \right)$, and $W_{ab}$ is the kernel function that depends on a distance between particles “a” and “b.” $\varPi_{ab}$ is the viscous term according to the artificial viscosity proposed by Monaghan (1992):

$$\varPi_{\text{ab}} = \left\{ {\begin{array}{ll} { - \frac{{\alpha_{v} . \bar{c}_{\text{ab }} . \mu_{\text{ab}} }}{{\bar{\rho }_{\text{ab}} }};} & {\varvec{v}_{\text{ab}} \cdot \varvec{r}_{\text{ab}} < 0} \\ {0;} & {\varvec{v}_{\text{ab}} \cdot \varvec{r}_{\text{ab}} \ge 0} \\ \end{array} } \right.$$

(14)

where $\varvec{r}_{\text{ab}} = \varvec{r}_{\text{a}} - \varvec{r}_{\text{b}}$, $\varvec{v}_{\text{ab}} = \varvec{v}_{\text{a}} - \varvec{v}_{\text{b}}$ are the particle position and velocity, respectively. $\alpha_{v}$ is a coefficient which needs to be adjusted in order to introduce the proper dissipation. In general, the parameter $\alpha_{v}$ is a free parameter which should be tuned for every specific problem [55]. As a practical instruction, it should be chosen as small as possible to avoid numerical instabilities without leading to over-diffusive behaviors, but it is not a mandatory rule for every problem. Sometimes, researchers consider a wide range and even large values for $\alpha_{v}$ to check its impact on the numerical results as a calibration parameter [56, 57]. In the current study, a wide range of various amounts of this parameter including: $0 \le \alpha_{v} \le 0.25$ is applied to check the numerical effects of $\alpha_{v}$ on results without instability and spurious oscillations in the scheme. $\bar{c}_{\text{ab}} = \frac{{ c_{\text{a}} + c_{\text{b}} }}{2}$ is the mean speed of sound for interactive particles, $\bar{\rho }_{\text{ab}} = \frac{{ \rho_{\text{a}} + \rho_{\text{b}} }}{2}$ is the mean density of interactive particles and $\mu_{\text{ab}} = \frac{{h . \varvec{v}_{\text{ab}} . \varvec{r}_{\text{ab}} }}{{\varvec{r}_{\text{ab}} . \varvec{r}_{\text{ab}} + \eta^{2} }}$ with $\eta^{2} = 0.01 \times h^{2}$.

Equations of ideal gases are as follows:

$$P = B\left[ {\left( {\frac{\rho }{{\rho_{0} }}} \right)^{\gamma } - 1} \right]$$

(15)

$$B = \frac{{c_{0}^{2} \cdot \rho_{0} }}{\gamma }$$

(16)

$$c_{0} = c\left( {\rho_{0} } \right) = \left. {\sqrt {\frac{\partial P}{\partial \rho }} } \right|_{{\rho_{0} }}$$

(17)

Parameter $B$ is a constant related to fluid compressibility modulus, and $\rho_{0} = 1000\,{\text{kg}}/{\text{m}}^{3}$ is the reference density chosen as the density at free surface; $\gamma$ is a constant which is normally from 1 to 7, and $c_{0}$ is the speed of sound at the reference density.

Methodology

The present study aimed to simulate the initiation and generation of water waves through underwater disturbance phenomenon according to application of SPH method. Results of adopted SPH model were compared with some experimental and field measurement studies focusing on the primary wave formation after cavity collapse and its propagation aspects.

As mentioned, the collapse of a bubble in a free surface is a really complicated multi-physical phenomenon in which two or three phases of material in the forms of gas, fume, and liquid are interacted with each other to release internal pressure of bubble and produce the first huge wave. Simulation of this complex event requires high computational cost and use of very time-consuming methods. On the other hand, simulation should be performed at the shortest possible time to predict the consequences of risks. In the case of disturbance, which generated water waves, duration of explosion and primary wave generation is between some milliseconds to some seconds that is really very small. On the contrary, modeling these sorts of events may take several hours.

Marine engineers prefer using simple models which are begun after bubble collapse phase by an implementation of initial conditions and try to solve a pure wave generation-propagation problem rather than a complicated multi-physics one at a reasonable time. Therefore, this article used a Lagrangian model and simulated waves by two stages:

• (1) At the first stage, it investigated that the flow after bubble collapse in free surface reached its maximum dimensions assuming that the flow had single-phase type by neglecting any two-phase flow effects, and it was found that the surrounding fluid was approximately at rest at the time of reaching the maximum bubble radius.

• (2) At the second stage, the water particles, which were thrown from crater volume into the around environment and returned again to the water surface, were considered in modeling.

New approach to initial free surface condition

Traditionally, mathematical analyses and Eulerian numerical models were well established for solving water waves’ problems due to the underwater explosion using predefined initial free surface conditions. Initial conditions were considered by different methods such as:

• (1) Empirical formula of geometric definition of initial dome-cavity shapes from direct observations,

• (2) Mathematical analyses of wave propagation data for description of cavity evolution over time

• (3) Multi-physics analysis of bubble generation, growth and collapse

However, results of different phenomenon analyses indicated a mathematical form of crater on the free water surface during the bubble collapse. This initial condition was then applied as a simple wave generator in various wave generation and propagation analysis.

Evolution of gas bubble due to the explosion, suddenly and at a very short time, produced a lot of changes in the geometry and volume of studied medium. This caused large displacement between water particles and splashed them into the air at the free surface. Simulation of these consequences was difficult or approximately impossible by Eulerian analysis techniques. Since it is impossible to separate fluid particles from each other in continuous models, the analysis results are sometimes completely different from real-time events in experimental or field observations. All efforts to improve continuous models for simulation of such complicated discretized phenomenon only led to increased complexity of models and also increased duration of numerical simulation. Meshless models such as the SPH are inherently discrete for simulation domain and equations, and thus it is much reasonable to analyze discrete phenomena with large deformations by these types of methods.

On the other hand, simulation of whole parts of phenomena from the first stages of underwater disturbance until the primary wave generation and then the wave propagation is a time-consuming activity. This process generates a huge source of progressive error in simulation domain. In addition, it requires a very complicated computer system with high cost.

The present study applied similar hypotheses like those defined in previous hypothesis models for the first type of analysis. The initial boundary condition of water surface is thus considered as a cavity at the first moments of primary wave generation in the meshless medium (see Fig. 8). In this case, we used the separation capability of material particles in Lagrangian model in addition to the traditional initial boundary conditions, and thus we compared differences and similarities of conventional methods with new aspects.

Fig. 8

Schematic geometry of numerical flume (a) and initial conditions of free surface deformation, including: b Parabolic nonzero volume function, c Parabolic zero volume function, d Quartic zero volume function)

In the previous type of simulations, one of the main ambiguities is related to the noncompliance with law of conservation of mass. Obviously, some parts of water mass are splashed and thrown into the air, where a nondiscretized model could not consider particles and their effects on behavior of wave domain, during the formation of crater-lip shape on the free water surface due to an underwater explosion occurrence. Some researchers assumed the volume of water in lip area equal to volume of water in crater area for considering mass conservation and compensation of water mass shortage. This hypothesis may produce exaggerated results in comparison with real conditions.

Results and effects of gas bubbles reaching the water surface were simulated because the explosion and its bubble burst were not modeled in this study. For simplicity, the amount of water mass and initial velocity of its particles were evaluated and considered in the SPH model. This secondary phenomenon was simultaneously modeled with a main event. Therefore, some of side effects, which were ignored in the conventional simulation, were considered for completion of wave generating behavior.

On the other hand, the water mass, which could be displaced from crater area, was calculated at the first step, and then the mass of lip and vaporized water should be equilibrated, and finally the remained mass was considered to be thrown upward with an initial upward velocity (see Fig. 9).

Fig. 9

Schematic geometry of numerical flume (a) and initial conditions of thrown upward masses (red parts), including: b one part mass, c three part masses, d five part masses

Numerical model

As mentioned in user manual of the DualSPHysics code [58, 59], it was first developed by SPH formulation in SPHysics (www.sphysics.org). This FORTRAN code is robust, reliable and programmed by C++ and CUDA languages to carry out simulations on the CPU and GPU, respectively (www.dual.sphysics.org). Furthermore, better approaches are implemented, for example, particles are reordered to give faster access to memory; and the symmetry is considered in the force computation to reduce the number of particle interactions; and the best approach is implemented to create the neighboring list by Domínguez et al. [60, 61]. The CUDA language manages the parallel execution of threads on the GPUs. The best approaches were considered for implementation as extensions of the C ++ code; hence, the most appropriate optimizations were implemented to parallelize particle interaction on GPU (Domínguez et al. [60, 61]). The DualSPHysics code was developed to simulate the real-life engineering problems using SPH models such as computation of exerted forces by large waves on the urban furniture of a realistic promenade (Barreiro et al. [62]), or study on the run-up in an existing block armor sea breakwater and wave forces on coastal structures (Altomare et al. [52, 53]).

DualSPHysics 3.1 is used in the present study and it requires hardware with a Central Processing Unit (CPU) or a Graphical Processing Unit (GPU). The computational efficiency offered by the GPU makes high-performance computing ready for computational fluid dynamics applications especially in very large modeling domains.

Two types of GPU cards on different machines were used in the present study. Applied machines and processors were as following:

• 1. GeForce GTX 680 with 1536 CUDA cores on a personal computer with a CPU type of AMD A8-3870 APU

• 2. GeForce GTX 780 M with 1536 CUDA cores on a MSI laptop with CPU type of Intel^® Core™ i7-4700MQ.

Assessment of the model and cases of application

Appropriate justification of the DualSPHysics was necessary to find whether the numerical model could reliably simulate free surface shock propagation phenomena due to different initial conditions before application of code for new approach. Therefore, first we chose and simulated an experimental study by Charlesworth (1945) and analytically solved problem by Bryant (1945) on the basis of Charlesworth studies. Finally, a famous large-scale test case from field test series of Mono Lake, which was reported by Whalin (1967) and LeMehaute (1995–1996), is considered for SPH simulation.

In this section, at first step, the initial boundary conditions are defined such as past studies by deformation on free surface of water body. It is tried to find the optimum size of models, number of particles, smoothed length parameter and have a comparison between SPH analysis and traditional techniques.

Multiple SPH models for above-mentioned cases were assessed by varying the some effective parameters. Besides, some other parameters are used on the basis of recommendations by software originators [58, 59]. The major parameters for each case are quoted in Tables 1 and 4. Effects of variation of different parameters were checked and found that inter-particle distance (or particle size) is the most critical parameter in this type of hydrodynamic problems. For very large or very small sizes of particles, the waves were dissipated or damped very quickly due to the low accuracy in very large sizes and numerical viscosity effects in very small sizes. To detect the best size of particles, the initial inter-particle distance (dp) is considered as a fraction of depth of crater, ranges from 1/5 to 1/60 for different cases (see Tables 1, 2, 4 and 5). The RMSE and correlation coefficient of each simulation was assessed, and finally, the reliable size of particles is discovered (see Table 6). So, at the rest of the study, the optimum size was found and used for simulation of the final cases of each series.

Table 1 SPH model parameters of the simulation of Charlesworth’s experiment and Penney’s analytical solution proposed by Bryant

Table 2 SPH model parameters of the simulation of Charlesworth’s experiment impact of inter-particle distance on run time of model

Besides, in these analyses cases, various viscosity values are used in SPH analysis. Results showed that, by reducing viscosity number, the better water elevation prediction could be obtained. Three examples of SPH simulation with different values of viscosity are shown in Fig. 10. In these samples, artificial viscosity parameter (which referred by vis in Figs. 10 and 11) varied from 0.0 to 0.25 for studying and control of viscosity effects in the numerical model (see Table 1). On the basis of DualSPHysics developers, the interaction between fluid and boundaries during shock wave propagation (such as dam break problem) becomes more relevant and the value of $\alpha_{v}$ should be changed according to the type of problem and its resolution or particle size for each case study to obtain accurate results [58].

Fig. 10

Comparison of Charlesworth’s experimental data with SPH results at X = 16.8 m from explosion location (with different artificial viscosity parameter)

Fig. 11

Comparison of Bryant’s analytical solution with SPH results at X = 16.8 m from explosion location (with different artificial viscosity parameter)

Another parameter, which has been assessed, is smoothing length. In DualSPHysics software, a variable coefficient is defined as a multiplier of geometrical distance between particles in different problems, as following equation:

$$h = \left\{ {\begin{array}{ll} {{\text{coef}}_{h} \times \sqrt {3d_{p}^{2} } } &\quad {3 \,{\text{dimensional}}\;{\text{problems}}} \\ {{\text{coef}}_{h} \times \sqrt {2d_{p}^{2} } } &\quad {2\,{\text{dimensional}}\;{\text{problems}}} \\ \end{array} } \right.$$

(18)

where $h$ is smoothing length, $d_{p}$ is inter-particle distance and ${\text{coef}}_{h}$ is a free coefficient. In the current study, the coefficient is varied from 0.8 to 1.5 (see Table 3). Assessment of models showed that in this type of problems the smoothing length, have not considerable impact on the run time or the speed of analysis. But, as shown in Table 3, the optimum value of smoothing length coefficient which minimizes the run time has been selected.

Table 3 SPH model parameters of the simulation of Charlesworth’s experiment impact of h_smooth on run time of model

In this study, we have single waves generated by water deformation or thrown mass system as a numerical symbol of water waves generated by underwater explosion. This type of waves is propagated as a major dissipative wave which is followed by a train of minor waves. So, to avoid wave reflection in models, for all simulations, it is checked that:

• 1. The length of the wave train to be less than the straight length of flume by trial and error.

• 2. It is monitored that when the wave train passed the wave gauge station, the simulation to be stopped. For this purpose, a straight length of the flume, about 2.5–3 times of the distance between gauge location and center of the flume, was found to be sufficient in our cases.

• 3. For more confidence, the flume was designed symmetrically (because this type of wave is propagated in both directions) and dissipative beaches with approximately 11° slope are considered on both sides (see Figs. 8 and 9).

It should be mentioned that the optimum slope of the beach was found by trial and error and comparing the results with the results of a very long flume (about 10 times the wave train size).

• A. Charlesworth experiments [8] and Bryant analytical cases [10]

Charlesworth experiences were performed at the Road Research Laboratory in London, in an open field test environment. These experiments included a series of underwater explosions within a semi-rectangular bay, with limited banks in west and south directions. Water depth was approximately uniform and about 5 meters with variable charge depths. Wave amplitudes in specified locations were captured by an analog camera on the south bank. In the present study, the recorded time history of surface waves amplitudes, produced by a 14.5 kg charge detonated in a water depth of 2.44 m, are considered for SPH simulations. The generated wave shapes and behavior of propagated waves at primary stages were monitored due to the initial crater formation of underwater explosion. Prior to application of DualSphyics for modeling experimental cases, this simple wave propagation was tested due to the initial conditions of free water surface deformations, and then the wave shapes were extracted for comparison of simulation results with real or analytical collected data.

A relative consistency between experimental and SPH results are presented in Fig. 10. The trends of SPH results are rationally compatible with the experimental record. Two first peaks are approximately simulated with a shift in occurrence time which becomes greater from the first to third crest in the time history curve (see Fig. 10). In this case, some differences are between numerical model and test results including: phase shift of third peak point, The value of the first curvature lowering is lower than the results of the experimental model, because in the numerical model of the initial deformation, the surface of the water is simulated as a crater, which diffuses over the time due to this downward deformation over time. The magnitude of positive peaks is approximately the same in both numerical and physical tests, but negative peaks are not simulated satisfactorily. The main cause for these differences is related to the initial boundary condition by water-free surface deformations. More precisely, as discussed in “Initial conditions of free surface” section of this article, the mathematical equations presented for the initial boundary conditions of the water surface have two basic weaknesses. First, some of them do not observe the mass conservation law. Second, all of these functions have discontinuities in the free surface of the water that do not correspond physically with the real behavior of the phenomenon. Basically, these two defects cause the results of the prediction of the generated waves by the underwater explosion are not compatible with experimental results.

The experimental data from Charlesworth studies were also applied by Bryant (1945) to validate the Penney’s theoretical formula for initiation of water waves and cavity formation. Analytical solution proposed by Penney (1945) for initial condition of cavity formation due to underwater explosion, was examined by Bryant (1945). In this case, both initial conditions, Penney’s theory and modified Penney’s curve as described by Bryant (1945), were tested in simulations. The initial surface condition was considered to be quadratic with characteristics in Bryant’s work for both SPH models of Charlesworth experiments on the basis of Penney’s studies [9]. Various types of SPH models were prepared for these samples, and thus their simulation parameters were similar to the previous SPH modeling case presented in Table 1. There is a reasonable consistency between two curves (see Fig. 11).

• B. Mono Lake field test case [49]

Different experimental programs including detonation of multiple large explosive charges under water were conducted at Mono Lake, California during 1966 to 1969. The primary objective of the programs was measurement of air blast from large bursts. The secondary objective was measurement of underwater shock waves and the bulk cavitation phenomena. This was done to evaluate effects of underwater pressure and the bulk cavitation on the air blast field as well as acquiring useful knowledge for prediction of damaging effects of cavitation closure on ships and submarines. The underwater explosion division mapped the underwater pressure field in order to achieve this objective. The Mono Lake field tests provided much data on generation, propagation, shoaling, breaking, and run-up of water waves produced by explosion in deep water. One of recorded data of these field tests was considered for monitoring the simulation results with real data series according to reports by LeMehaute et al. [12, 48] (see Fig. 12) who collected data from Whalin test reports in 1967. Also, Fig. 12 shows the analytical simulation of this set of data by linear and nonlinear models on the basis of LeMehaute et al. researches.

Fig. 12

Mono Lake test-recorded water level at a distance of 189.3 m from explosion location with linear and nonlinear numerical simulations reported by LeMehaute et al. (1998) for Charge weight of 4196 kg (9250 lbs.) at 0.18 m (0.6 ft)

Obviously, the linear numerical solution by LeMehaute et al. (1996) did not have a significant consistency to results of the field test. This discrepancy was modified by using advanced numerical techniques such as nonlinear models by them. They also found that the use of nonlinear analysis model produces better results in comparison with linear analysis model and has more convergence with field measurement around the first and second peaks. Of course, this improvement with high time-consuming calculations and use of a very complex numerical code can only be seen in the case of the first two-peak event. On the other hand, in the rest of the time history of the water surface variations, such as the values of the maximum points and the correspondence of other points in time, there are not valuable modifications.

In this part of study, the Mono Lake case is simulated by SPH method by using free surface deformation concept, so the capabilities of the SPH method and in particular the DualSPHysics code for simulation of collapse of initial cavity and generation of primary wave domain due to underwater explosion for different types of initial boundary conditions, are investigated.

The numerical simulation process of fluid particles during initiation of primary wave shapes and their radial propagation from explosion location toward all directions is related to physical properties at each SPH particle and its interaction with others. The wave shapes can be numerically measured by wave gauges in specified locations or by free surface waterline calculations. These techniques were applied in the following simulation test cases to assess results by experimental field test by other researchers.

At the first step, results of primary wave generation and its propagation are modeled considering the initial water surface deformation considered in analytical solutions performed by LeMehaute. Obviously, results of SPH modeling by initial water surface deformation are not very similar to test results (see Fig. 13 and Tables 4 and 5) same as results of linear and nonlinear solutions by LeMehaute (see Fig. 12). On the other hand, the SPH model results are very better than linear model for prediction of second and third peaks and even the value of the first peak is simulated very close to the test record. The major difference between SPH and experimental results is related to the effects of initial boundary condition definition by traditional geometric initial water line deformation. This weakness is also obvious in the results of linear numerical solution by LeMahaute (see Fig. 12). On the contrary, a simple SPH model, presents better compatibility with field data.

Fig. 13

Mono Lake test-recorded water level at a distance of 189.3 m from explosion location SPH results from Quadratic and Quartic water surface deformation as initial condition

Table 4 SPH model parameters of the simulation of Mono Lake field test case

Table 5 SPH model parameters of the simulation of Mono Lake field test case

By using the DualSPhysics software, the results show that the quadratic function can predict water levels better than quadratic. For first two peaks results in most of the times are similar, but after this stage the quadratic function could behave very better than quadratic as an initial condition. The main disadvantage of these results, which is based only on the initial deformation at the surface of the water, is the fall in the water level between 25 and 33 s, as well as the phase delay in the first peak of the curve. The reason for this difference with the experimental results is the imposed boundary condition and the change of water balance based on inexact experimental relationships for initial boundary condition (see Fig. 13).

Results of new approach and discussion

As a new point of view in this paper, by using the second type of boundary conditions in numerical SPH models, waterbody sections are selected on the basis of equating explosion energy to throw this part of water particles into outer environment of crater through application of discrete property of Lagrangian model. Waterbody size and its initial velocities are estimated by law of conservation of energy. This numerical test is performed several times by different partitioning of thrown water mass. Time history of the recorded wave at the same location indicates that the prediction of waves is more realistic than the initial surface deformation conditions (see Fig. 14).

Fig. 14

Mono Lake test-recorded water level at a distance of 189.3 m from explosion location SPH results from different thrown mass models instead of initial condition

Quantitative estimation of errors has been performed for LeMehaute numerical results and SPH models in comparison with experimental results and shown in Table 6. In this table, the value of RMSE and correlation coefficients is reported.

Table 6 Comparison of RMSE and Correlation coefficient of LeMehaute models vs. SPH models in comparison with experimental results of Mono Lake test (Reported by Whalin-1967)

Lower RMSE in models with thrown mass represents improvement of underwater explosion modeling in comparison with traditional initial boundary condition method. As per last descriptions in “Initial conditions of free surface” and “Assessment of the model and cases of application” sections, the geometric initial condition for free water surface may produce poor results for modeling of generated waves due to their discontinuity and sometimes their nonconservative characteristics about mass conservation. Besides, rate of rational RMSE and correlation coefficients show that SPH models behave better than traditional numerical models. It is important to note that the accuracy of SPH model is from the first and second order, but the linear and nonlinear analytical models have accuracy higher than the second order, but a simple SPH model can be predicted like the complicated analytical model and somewhere better than the traditional numerical simulation even by applying geometric initial boundary condition (see Figs. 12 and 13).

In the first group of numerical models, in which the initial boundary conditions were created by water-free surface deformation, results of analyses are shown in Fig. 15 in terms of water level variations as well as horizontal velocity of particles.

Fig. 15

Water wave evolution at different time steps, including: Quadratic (left), Quadratic with lip (middle), Quartic (right) horizontal (x) velocity of particles is shown by color spectrum

According to Fig. 15, water particles around the explosion crater obviously move toward the center of crater in the middle of model after being released in the beginning of simulation. Like the dam failure model, this displacement produces positive and negative waves. Positive waves interact with each other in the middle of model at the disturbance center; and negative waves move along the longitudinal direction of model and move away from the disturbance center. According to the simulation results, a reflection wave is produced and it is separated from disturbance center in the opposite direction to positive waves after positive waves collide with each other. Initial negative and reflected waves continue to affect each other and produce a complex wave field. In addition to this phenomenon, water particles also split from the main waterbody and interact again during the collision process due to the properties of the Lagrangian model; hence, this may increase the nonlinearity of phenomenon.

The following figure shows the horizontal velocity contours and water surface deformations in different time steps of numerical simulation for each initial condition (see Fig. 15).

In the second group models, some water mass sections, which are separated from the main waterbody with an initial velocity due to the explosion energy, return back and hit the free surface. This process automatically generates a crater, and thus like the first group models, there are positive and negative wave modes which affect each other. In addition, water particles, which are thrown upward, can produce the secondary waves. These secondary waves are combined with previous waves and cause a further increase in the nonlinear behavior of the wave system. This simulated behavior, which is more similar to the original phenomenon, makes deformation of free water level and different velocity components from results of the first group of numerical models.

The following figures show the velocity contours and water surface deformations in different time steps of numerical simulation for thrown mass condition (see Figs. 16 and 17):

Fig. 16

Water wave evolution at different time steps, including: 1 section of mass (left), 3 sections of mass (middle), 5 sections of mass (right) horizontal (x) velocity of particles is shown by color spectrum

Fig. 17

Water wave evolution at different time steps, including: 1 section of mass (left), 3 sections of mass (middle), 5 sections of mass (right) vertical (z) velocity of particles is shown by color spectrum

As a specific conclusion, it seems that thrown mass method can predict the water surface elevation suitably rather than initial water surface deformation. On the other hand, as a general idea, it could be concluded that thrown mass technique can represent better results than traditional methods such as water surface deformation.

In a more precise description, it should be noted that the launch of particles of water based on the energy balance of the explosion and considering the kinetic energy of the thrown mass equal to released energy by explosion in the numerical model may cause following results:

First, a more accurate volume of water will be evacuated from the main waterbody into the environment, and therefore the crater has more reliable dimensions.

Secondly, due to the return of water particles to the initial surface, while maintaining the law of mass conservation in the simulation environment, the secondary effects of the collision of these particles and their participation in the generation of the wave resulting from the phenomenon of the underwater explosion are more accurately simulated. In this way, the results are more in line with the field test results (Fig. 13).

Summary and conclusion

Theoretically, the initial boundary conditions are used on the water surface to produce waves caused by an underwater disturbance. In most cases, results of forecasted waves from these boundary conditions do not comply with field and laboratory studies, and strictly implement results of a particular test. Using a numerical Lagrangian model with two views, the present study tried to obtain the more accurate simulation of water wave generation due to the underwater disturbance phenomena.

Like other conventional methods, the first method applied the initial boundary conditions for simulation domain and allowed material particles in the computed space to be discrete from each other during the phenomenon development using the Lagrangian properties. Therefore, some results such as splash of fluid particles and large displacement between their sections could be observed and they might show the more realistic behavior than results of Eulerian models.

In the second method, a section of waterbody was separated due to the explosion potential and it thrown into the upward direction by an initial velocity. Equating the energy-releasing explosion and the kinetic energy of this section of water mass, the initial size and velocity of thrown waterbody were calculated and simulated in the SPH model. The second method of modeling had more realistic conditions than the first method. On the other hand, some nonlinear behavior of wave generation in an underwater disturbance event was considered in the latter methodology.

According to results of both approaches and traditional method, it seems that they led to better wave prediction.

Generation of the first leading wave of initial cavity-type conditions for free surface of sea water line was a typical shock wave which was very high and unstable due to its extraordinary steepness. This primary wave was often the largest and strongest wave among other waves in a trail of underwater disturbance surface waves. Prediction of leading wave and calculation of its properties is important for designing the coastal and marine structures that are located in the effective domain of leading wave. Smoothed-particle hydrodynamics is a proper numerical method for prediction of turbulent and harsh conditions of surface water waves.

The present research concluded that:

• (1) SPH model can predict first two or three leading waves. It is found that the SPH model prediction has rational consistency with experimental record or analytical solution (see Figs. 10 and 11).

• (2) According to the initial surface deformation, the history of waves has time shift in comparison with thrown mass models in SPH environment. On the other hand, thrown mass SPH models behave better than SPH models of initial surface deformation or other analytical models to predict all peaks of water wave in a time history of water elevation in a measured station (see Figs. 12, 13 and 14).

• (3) Discrete behavior of SPH models is the main difference between analytical and traditional numerical models with SPH models. This feature makes it more suitable for modeling the shock phenomena. For instance, when the initial cavity form of water surface starts collapsing, it is very hard for traditional models to simulate mixed multiple layers of fluids, but it is inherently simulated by SPH method (see Figs. 15 and 16).

• (4) Models with thrown mass are suitable for experimental data and better than the initial condition simulations. Considering more realistic situation in thrown mass models, the mass of these models are conserved, and finally the water levels are more compatible with experimental results. Consider that, the primary trough in time history of model with initial surface deformation (Fig. 13) is reduced and balanced in thrown mass model (Fig. 14).

• (5) It was found that the results of water level prediction in different times are affected by initial condition. So it is very important for simulation purposes that a reliable method could be presented.

• (6) It is very important for modeling a phenomenon that, the run time and efficiency of model could be managed and optimized to obtain good results. Using SPH model, let us a good chance to model initial condition more realistic. On the other hand, Lagrangian properties of this simulation technique help us for reproducing natural initial condition (see Table 6).

• (7) By using thrown mass idea, a more detailed and accurate initial boundary condition, is applied in numerical model. Besides, this idea helps us to conserve mass balance of water body. In this way, extra secondary waves and their effects on wave field are considered accurately.

• (8) A good prediction of wave behavior can be made by application of simple SPH models and considering real hypotheses in a short simulation time (see Tables 2 through 4). However, it is necessary to apply complicated high order nonlinear analyses to predict wave shapes and their propagation in domain according to analytical calculations.