Introduction

The goal of plasmonics is to study interaction between light and matter through surface plasmon resonance (SPR) for a diversity of properties [1]. Optical bistability (OB) is a nonlinear phenomenon characterized by certain resonant optical structures, which can switch between two different stable transmission states for one given input [2]. OB has been observed in different kinds of media such as atomic media [3] and nanoplasmonic structures [4,5,6,7,8]. OB devices could be applied for high-speed processing of optical signals such as all-optical switching [9, 10], optical transistor [11, 12], and optical memory [13, 14]. Since the optical Kerr effect leads to the possibility of controling light by light, one way for observing the hysteresis response to the input field is investigating the optical Kerr effect in plasmonic structures [15].

Noble metals are the obvious choice among metals for many plasmon-based applications in the visible spectrum, because of the very narrow resonance. Nevertheless, metals present high nonradiative losses that lead to unwanted heating limiting some of their applications in photonics. Opportunely, graphene with extremely large Kerr nonlinearity has fascinated enormous research interest because of its exceptional properties in terahertz to mid-infrared applications [16, 17]. Nowadays, the terahertz to mid-infrared spectrum, which typically ranges from 10 to 4000 cm\(^{-1}\), is finding a wide variety of applications in information and communication, medical sciences, chemical and biological sensing, spectroscopy, among many others [18,19,20]. The great potential of graphene is in photonics, optoelectronics and plasmonics [21,22,23,24,25,26]. Other exhibited optoelectronic graphene devices include ultrafast lasers and broadband polarizers [27]. Furthermore, by considering the zero bandgap, short carrier lifetime, and high carrier mobility a graphene-based photodetector in high-speed communication links has been offered [28]. The hybrid Airy plasmons for the first time by taking a hybrid graphene-based plasmonic waveguide in the terahertz (THz) domain have been revealed [29]. One of the main shortcomings in the realization of graphene optoelectronic devices is the low photocurrent created by a single-layer graphene sheet. In order to overcome this issue, metal nanoparticles were included in the system to enhance the photocurrent, and specific wavelength detection can be achieved by varying the structure of the metal nanoparticles simultaneously [30]. The existence of graphene near the metal nanoparticles subsequently alters the physical environment of the localized surface plasmon resonance (LSPR) excited in the metal nanoparticles [31].

Recently, it is shown that in addition to strengthening the local plasmonic fields, graphene also can generate large nonlinear effects [32,33,34,35,36]. OB in graphene-based composite consisting of graphene-wrapped dielectric spherical nanoparticles has been studied theoretically [37, 38]. In optoelectronics aspects, there also has been a great deal of interest in studying the optical properties of graphene due to its abundant potential applications within a wide spectral range from terahertz to visible frequencies [37].

In this study, since graphene can be used as coating material, we study a optical bistability of a graphene-wrapped plasmonic nanoparticles with cylindrical geometry. It is found that the threshold values of both OB and optical tristability (OT) are tunable either by varying the particle environment parameter or the graphene parameters. The considerable unknown area still remains for terahertz technology due to a lack of affordable and efficient sources and detectors [39]. The frequency of graphene plasma waves lies in the terahertz range, as well as the gap of graphene nanoribbons, and the monolayer graphene tunable bandgap, making graphene appealing for terahertz generation and detection. Therefore, graphene-based devices can be used for terahertz detecting and sensing.

Theoretical model and methods

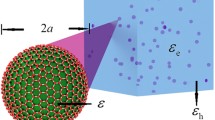
We develop a theoretical scheme based on a composite consisted of the graphene-coated core–shell nanoparticles with cylindrical structure embedded in a host matrix. The radius of core and shell is a and b, respectively, in which the geometric aspect ratio is defined as \(\eta = a^{2}/b^{2}\). We suppose that graphene coated on the core (a), graphene wrapped on the outer surface of the shell (b), and graphene wrapped on the core and shell instantaneously (c), as shown in Fig. 1. According to this figure, the green color presents the monolayer graphene with Kerr-like nonlinear surface conductivity. The permittivity of the core, shell and host medium are given as \(\varepsilon _{c}\), \(\varepsilon _{s}\) and \(\varepsilon _{h}\), respectively, and the surface conductivity of graphene is \(\sigma\).

Fig. 1
figure 1

Schematic of cylindrical core–shell nanoparticle with graphene wrapping on the core (a), the shell (b), and the core and shell (c). The green color presents the monolayer graphene

Full size image

The calculations and simulations are performed for three different models of graphene placement on the surface of the core–shell nanoparticles. Here, the calculations are written for the third situation (c) in which, two other situations can be derived from that.

Owing to the size of nanostructure is assumed much less than the wavelength of incident light, the quasi-static approximation is valid, and the Laplace equation can be solved as following

$$\left\{ {\begin{array}{ll} {V_{c} = - E_{0} \rho \cos \phi + A\rho \cos \phi } & {\rho \le a} \\ {V_{s} = - E_{0} \rho \cos \phi + B\rho \cos \phi + C\rho ^{{ - 1}} \cos \phi } & {a \le \rho \le b} \\ {V_{h} = - E_{0} \rho \cos \phi + D\rho ^{{ - 1}} \cos \phi } & {\rho \ge b} \\ \end{array} } \right.$$
(1)

The unknown coefficients can be determined by the boundary conditions as follows,

$$\begin{aligned} & \hat{n} \times (\vec{E}_{s} - \vec{E}_{c} )|_{{r = a}} = 0 \\ & \hat{n} \times (\vec{E}_{h} - \vec{E}_{s} )|_{{r = b}} = 0 \\ & \hat{n}.(\vec{D}_{s} - \vec{D}_{{Dc}} )|_{{r = a}} = \rho _{1} \\ & \hat{n}.(\vec{D}_{h} - \vec{D}_{s} )|_{{r = b}} = \rho _{2} \\ \end{aligned}$$
(2)

where \(\rho _{1}\) and \(\rho _{2}\) are the surface charge density of graphene on the inner and outer surface of shell, respectively, and have the relation \({\mathbf{\triangledown .j_{||}}} = i\omega \rho\) with the surface density of linear current \({\mathbf{j_{||}}} = \sigma {\mathbf{E_{||}}}\) at the frequency \(\omega\). Monolayer of graphene as a two-dimensional material, its thickness is extremely small around 0.34 nm compared with the thickness of nanocylinder. Consequently, we will treat it as a conducting film with surface conductivity \(\sigma\) with a realistic approximation [40, 41]. Hence, the source-free boundary conditions could be applied for the monolayer graphene-coated core–shell [37, 38]. The coefficients A, B, and C are determined by applying the boundary conditions at the inner and outer boundary after some algebraic calculations

$$\left\{ {\begin{array}{*{20}c} {A = \frac{{(\varepsilon _{c} - \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} - \varepsilon _{h} - \Theta _{2} )\eta }}{{(\varepsilon _{c} - \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} - \varepsilon _{h} - \Theta _{2} )\eta + (\varepsilon _{c} + \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} + \varepsilon _{h} + \Theta _{2} )}}E_{0} } \\ {\quad + \frac{{\varepsilon _{c} (\varepsilon _{s} + \varepsilon _{h} + \Theta _{2} ) + \varepsilon _{s} (\varepsilon _{s} - 3\varepsilon _{h} + \Theta _{1} + \Theta _{2} ) + \Theta _{1} (\varepsilon _{h} + \Theta _{2} )}}{{(\varepsilon _{c} - \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} - \varepsilon _{h} - \Theta _{2} )\eta + (\varepsilon _{c} + \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} + \varepsilon _{h} + \Theta _{2} )}}E_{0} } \\ {B = \frac{{(\varepsilon _{c} - \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} - \varepsilon _{h} - \Theta _{2} )\eta + (\varepsilon _{c} + \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} - \varepsilon _{h} + \Theta _{2} )}}{{(\varepsilon _{c} - \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} - \varepsilon _{h} - \Theta _{2} )\eta + (\varepsilon _{c} + \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} + \varepsilon _{h} + \Theta _{2} )}}E_{0} } \\ {C = \frac{{2\varepsilon _{h} (\varepsilon _{c} - \varepsilon _{s} + \Theta _{1} )a^{2} }}{{(\varepsilon _{c} - \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} - \varepsilon _{h} - \Theta _{2} )\eta + (\varepsilon _{c} + \varepsilon _{s} + \Theta _{1} )(\varepsilon _{s} + \varepsilon _{h} + \Theta _{2} )}}E_{0} } \\ \end{array} } \right.$$
(3)

where \(\Theta _{1} = \frac{i\sigma }{\omega a \varepsilon _{0}}\) and \(\Theta _{2} = \frac{i\sigma }{\omega b \varepsilon _{0}}\).

By considering the nonlinear and local tangential field dependent surface conductivity of the monolayer graphene as only one atom thick structure, the surface conductivity can be modeled as following [37].

$$\begin{aligned} {\mathbf{\sigma }} = \sigma _{0} +\sigma _{3} \mid E_{t} \mid ^2 \approx \sigma _{0} +\sigma _{3} < \mid E_{t}\mid ^2>_{g}, \end{aligned}$$
(4)

without considering the external magnetic field and under the random-phase approximation, the frequency dependent surface conductivity of graphene \(\sigma _{0}\) is written as the superposition of the intraband \(\sigma _{\mathrm{intra}}\) and the interband term \(\sigma _{\mathrm{inter}}\) [42].

$$\begin{aligned} \sigma _{0}= & {} \sigma _{\mathrm{intra}}+ \sigma _{\mathrm{inter}},\nonumber \\ \sigma _{\mathrm{intra}}= & {} \frac{ie^2k_{B}T}{ \pi \hbar ^2( \omega +i/ \tau )}\left[ \frac{E_{F}}{k_{B}T} +2Ln(e^{ \frac{-E_{F}}{k_{B}T}} +1\right] ,\nonumber \\ \nonumber \\ \sigma _{\mathrm{inter}}= & {} \frac{ie^2}{4 \pi \hbar } Ln\left[ \frac{2E_{F}-( \omega +i/ \tau )}{2E_{F}+( \omega +i/ \tau )} \right] , \end{aligned}$$
(5)

where \(\omega\), \(E_{F}\), \(\tau\), \({\text{T}}\), \(v_{F}\), e, \(k_B\) and \(\hbar\) are the frequency of the incident field, Fermi energy, the electron-phonon relaxation time, the temperature , the Fermi level of graphene, the elemental electron charge, the Boltzmann constant, and the reduced Planck constant, respectively. When the Fermi energy \(E_{F}\) is much more than photon energy, the interband transitions in graphene are negligible compared with the intraband part. Therefore, in THz range graphene can be described by the Drude-like surface conductivity \(\sigma _{\mathrm{intra}}\).

Since the graphene is a nonlinear material, the nonlinear conductivity coefficient \(\sigma _{3}\) for graphene is given by [43]

$$\begin{aligned} \sigma _{3}=-i \frac{9}{8} \frac{e^2}{ \pi \hbar ^2} \frac{(ev_{F})^2}{E_{F} \omega ^3}, \end{aligned}$$
(6)

Moreover, the dielectric function of a plasmonic noble metal is described by the Drude model and given by \(\varepsilon (\omega ) = \varepsilon _{\infty }- \frac{\omega _p^2}{\omega (\omega +i\gamma _{F})}\), where \({\omega_{p}}\), \({\gamma_{F}}\) and \({\varepsilon_{\infty}}\) are the plasma frequency of the metal, the collision frequency of free electrons and the high-frequency part of the dielectric function [44]. In this study, gold is used for the core and the relevant parameters of gold are as follow: \({\omega_{p}^{Au}} = 8.9\) eV, \({\varepsilon_{inf}^{Au}} = 6.9\), and \({\gamma _{F}^{Au}} = 0.072 eV\).

Results and discussion

In this section, it is numerically demonstrated that it is possible to obtain OB from plasmonic core–shell nanoparticle with cylindrical structure by considering graphene wrapped on the surface of the structure. In this arrangement, more means to control OB, such as, the surrounding media, the Fermi energy of graphene and interfacial parameter are discussed. Plasmonic core–shell nanoparticles consist of a layer grown over a metallic golden core, are a comparatively new category of plasmonic nanoparticles or nanoshells that have recently received increased attention owing to their large and interesting optical properties and also ability to manipulate the light in unique methods. According to Fig. 1, the average of the local electric field square in the core as a function of the external applied field is plotted for different parameters in order to investigate the influence of different parameters on the controllability and tunability of OB.

Fig. 2
figure 2

Dependence of bistability of the local core electric field intensity \(|E_{c}|\) versus the external incident field \(|E_{0}|\) on graphene when graphene is on the golden core and shell surface. Parameters are \(\textit{b}=15\) nm, \(\eta = 0.7\) \(E_{F} = 0.6\), \(\varepsilon _{s}= 5.5\), \(\varepsilon _{h}=2.25\), \(\tau = 0.1\) ps, and \(\lambda = 25\,\upmu\)m

Full size image
Fig. 3
figure 3

Optical bistability curves \(|E_{c}|\) as a function of the incident applied field \(|E_{0}|\) for a core–shell nanoparticle for different values of \(\eta\), graphene is on a the golden core surface b the shell surface c on the golden core and shell surface. \(\textit{b}=15\) nm, \(\varepsilon _{s}= 5\), \(\varepsilon _{h}=2.25\), \(\tau = 0.1\) ps, and \(\lambda = 25\,\upmu\)m

Full size image

Strong interaction between light and plasmons leads to large electromagnetic field enhancement [45]. In the other words, the surface plasmon resonance could induce large local electromagnetic fields that its tunability to a desired wavelength is greatly beneficial [31]. Metallic nanoparticles are capable of enhancing and confining the electromagnetic field under external illumination via the excitation of surface plasmons the collective oscillations of conduction electrons. The degree of confinement is dependent on particle size, shape, composition, and relative arrangement. In the graphene-based nanoparticles, the nonlinear dependence of conductivity of graphene (\(\sigma _{3}\)) plays an essential role in observing OB in the range. In THz frequency range, the imaginary part of the surface conductivity of the graphene is positive and behaves as a metal structure which could support local surface plasmons. Consequently, OB in THz frequencies ranges for graphene-wrapped nanoparticles can be attained [42].

Fig. 4
figure 4

Optical bistability curves \(|E_{c}|\) as a function of the incident applied field \(|E_{0}|\) for a core–shell nanoparticle for different values of Fermi energy, graphene is on a the golden core surface b the shell surface c on the golden core and shell surface. \(\textit{b}=15\) nm, \(\varepsilon _{s}= 5\), \(\varepsilon _{h}=2.25\), \(\tau = 0.1\) ps, and \(\lambda = 25\,\upmu\)m

Full size image
Fig. 5
figure 5

Optical bistability curves \(|E_{c}|\) as a function of the incident applied field \(|E_{0}|\) for a core–shell nanoparticle for different values of \(\varepsilon _{h}\), graphene is on a the golden core surface b the shell surface c on the golden core and shell surface. \(b =15\) nm, \(\varepsilon _{s}= 5\), \(\tau = 0.1\) ps, and \(\lambda = 25\,\upmu\)m

Full size image
Fig. 6
figure 6

Optical bistability curves \(|E_{c}|\) as a function of the incident applied field \(|E_{0}|\) for a core–shell nanoparticle for different values of \(\tau\), graphene is on a the golden core surface b the shell surface c on the golden core and shell surface. \(b=15\) nm, \(\varepsilon _{s}= 5\), \(\varepsilon _{h}=2.25\), and \(\lambda = 25\,\upmu\)m

Full size image

To investigate the impact of graphene on OB, the average local core field as a function of the applied electromagnetic field is plotted, in the presence of graphene (red line) and absence of graphene (blue line) via considering the metallic gold core. It shows that in the absence of graphene, the electromagnetic field has almost a direct relationship with the applied field, and for this, reason OB phenomenon does not happen and no noticeable OB in THz frequencies range is observed in Fig. 2 . It is clear that nanolinear core–shell nanostructure would show optical bistability even without monolayer of graphene, but not in THz range [8]. Therefore, graphene is the main responsible for nonlinearity and OB in the proposed model in THz which is attractive for biomedical imaging, security, remote sensing and spectroscopy [39].

The average of the core field within the metallic core as a function of the applied field for different values of \(\eta\) for three different positions of graphene is plotted in Fig. 3. With fixed shell radius at \(\textit{b}= 15\) nm, by increasing the \(\eta\) as a geometric aspect ratio of nanoparticle, the bigger radius of metallic core would increase the surface plasmonic resonance hence assists the nonlinearity in the system.

As demonstrated in Fig. 4, OB is sensitive to the Fermi energy for all graphene positions. By increasing the Fermi energy of monolayer graphene, threshold of bistability increases, and the hysteresis loop becomes wider. OB is found very dependent on the Fermi energy of graphene, in which with increasing this parameter, an increase in the bistable switching-up threshold field is obvious.

The influence of surrounding medium on OB is exhibited in Fig. 5. The nonlinearity response of the system strongly depends on \(\varepsilon _{h}\). The system interestingly exhibits Optical tristability (OT) with changing the optical properties of host. OT is a phenomenon that implies for an input power, the system exhibits three different output intensities. This result means that, the transition from two different output intensities (OB) to three different output intensities (OT) or vice-versa can be controlled by the graphene coating on the different media surrounding the core–shell nanoparticle, which will have more advantages than the OB in some applications where more than two states are needed [46].

In addition to the effect of mentioned parameters, it is shown that the relaxation time of graphene can influence OB in Fig. 6. It is known that the long relaxation time induces a low dissipation in graphene, therefore, broader OB loop could be obtained via longer relaxation time which confirms our simulations. The possibility of tuning the electronic and optical properties by external means such as optical pump, makes graphene suitable for terahertz radiation manipulation.

Conclusion

In conclusion, OB phenomena of a graphene-wrapped cylindrical core–shell nanostructure is theoretically investigated. Results show that graphene exhibits a very strong optical nonlinearity in the terahertz spectral region. Moreover, we demonstrated that the hysteresis responses strongly depend on diverse parameters such as the Fermi energy and relaxation time of graphene and interfacial parameter. By applying appropriate parameters of the system, switching from OB to OT would be achieved that to be particularly promising next generation of all-optical sensors. Optical transformation and nonlinearity are found in graphene-based devices, which are suitable for applications in electronics, optics, energy storage and THz technology. Moreover, the fine biocompatibility of graphene makes it a very good applicant for applications in biotechnology and medical science. The move to a graphene-based technology in THz should make them more viable. Therefore, designing such as these new graphene-based systems would be valuable.