Introduction

Problems of scheduling occur in many economic domains, such as airplane scheduling, train scheduling, time table scheduling and especially in the shop scheduling of manufacturing organizations. A flexible flow shop (FFS), which is also known as hybrid flow shop or flow shop with parallel machines, consists of a set of machine centres with parallel machines. In other words, it is nothing but an extension of the simple flow shop scheduling problem (FSP). In real practice, a shop with a single processor at each stage is rarely encountered. Generally, processors are duplicated in parallel at stages. The purpose of duplication is to balance the capacity of stages, increase the overall shop floor capacity, reduce, if not eliminate, the impact of bottleneck stages and so on. A flexible flow shop scheduling problem (FFSP) has M jobs with ‘g’ number of operations to be carried out in ‘g’ stages. Each job n (n = 1, 2, …, M) is to be sequentially processed at each stage t (t = 1, 2, …, g). Each stage t (t = 1, 2,…, g) has MTt identical machines. At least one stage will have more than one machine and only one operation is carried out in each stage. The parallel machines in a stage are identical and take same time to process an operation. At any given time, a machine can process only one job. The processing time of each job m at a stage t ‘‘p (n, t)’’ is deterministic and it is known in advance. The objective is to find permutation of all jobs at each stage so as to reduce the makespan. For a scheduling problem, the makespan is defined as the completion time of the last job to leave the production system (Pinedo 2008). Among all the shop-scheduling problems, flexible flow shop problem (FFSP) is treated as one of the difficult NP-hard (Non-deterministic polynomial time) problems as pointed out by Gupta (1988) and Hoogeveen et al. (1996). It is unlikely that an exact solution to FFSP can be found by a polynomial time algorithm. However, an exact solution can be obtained by various methods of reduced enumeration, typically by a branch and bound (B&B) algorithm. In any case, only small-size instances can be handled by exact methods. To find a good solution for large size problems of practical interest within an acceptable amount of time, two types of algorithms, such as (1) approximation algorithms and (2) heuristic or meta-heuristic algorithms, are used. An algorithm is called an approximation algorithm if it is possible to establish analytically how close the generated solution is to the optimum (either in the worst-case or on average). The performance of a heuristic algorithm is usually analyzed experimentally, through a number of runs using either generated instances or known benchmark instances. Heuristic algorithms can be very simple but still effective. Some of modern heuristics based on various ideas of local search are listed as neighbourhood search, tabu search, simulated annealing, genetic algorithms, etc.

Even though the performance of exact methods such as branch and bound is superior to heuristic and meta-heuristic techniques, exact methods fail to solve large size problems. On the other hand, heuristic techniques are problem-dependent and easily get trapped at the local optimum. To overcome the drawbacks of both exact and heuristic methods, researchers focus on meta-heuristic approaches which happen to be problem-independent and applied to solve problems independent of their size. Recently, many meta-heuristics have been applied in recent past to solve the FFSP to generate near-optimal solutions in a reasonable computation time (Oguz and Ercan 2005; Engin and Doyen 2004; Niu et al. 2009; Cui and Gu 2015). Usually, meta-heuristics are population-based algorithms which can be broadly classified into two groups. They are evolutionary algorithms (EA’s)- and swarm intelligence (SI’s)-based algorithms. Some of the famous EA’s are genetic algorithm (GA), evolution strategy (ES), differential equation (DE), evolutionary programming (EP), etc. Some of the famous swarm intelligence-based algorithms are particle swarm optimization (PSO), ant colony optimization (ACO), fire fly algorithm (FF), artificial bee colony (ABC) algorithm, etc. Other than these two broad categories, there are other population-based algorithms, such as harmony search (HS), bio-geography-based optimization (BBO), eco-geography-based optimization (EBO) and gravitational search (GS) algorithm, etc. Most of these algorithms have one thing in common, i.e. tuning of the respective algorithm-specific parameters. For example, GA contains parameters, such as mutation and crossover probabilities. PSO contains parameters, such as inertia weight and acceleration constants. Artificial bee colony (ABC) uses the number of scout bees, onlooker bees and employed bees. HS uses pitch adjusting rate and memory consideration rate. Similarly, other algorithms also have their own tuning parameters. To obtain good optimized solutions to specific problems, tuning of the algorithm-specific parameters is essential. Since finding the right tuning parameters is a difficult task, an efficient tuning parameter-less algorithms is required to overcome this drawback. Teaching–learning-based optimization (TLBO) and JAYA are some of the recent optimization techniques that were proposed without any algorithm-specific tuning parameters in comparison with any other meta-heuristics. The present work focuses on the application of TLBO and JAYA algorithms to solve FFSP. TLBO, proposed by Rao et al. (2011), has been applied to different kinds of optimization problems in the past and found to be one of the good algorithms solving NP-hard problems. JAYA algorithm is proposed by Rao (2016) recently. It is observed that JAYA algorithm seems to be an efficient one in solving the constrained and unconstrained optimization benchmark problems. Hence, an attempt is made in this work to apply JAYA to solve FFSP. Further, TLBO is a two-phase algorithm, whereas JAYA solves the optimization problem in a single phase.

The meta-heuristics in the present work also require some improvements in the basic algorithm so that their efficiency may be improved in generating the optimal or near-optimal solutions. Many researchers have embedded local search techniques with meta-heuristics to improve the efficiency of meta-heuristics. For example, Wang et al. (2011) have used a local search technique to simulated annealing (SA) to improve its efficiency while solving FFSP. Choong et al. (2011) have proposed hybrid algorithms combining tabu search (TS) and simulated annealing (SA) to particle swarm optimization (PSO) to improve efficiency of PSO in solving FFSP. Liao et al. (2012) have used a local search technique to PSO. Therefore, a new local search technique is proposed in the present work to improve the solution quality of FFSP generated by present algorithms. Although these algorithms seem to be elegant, they lose solution diversity after some iteration and may get trapped at the local optima. To overcome this drawback, mutation strategy from genetic algorithm is incorporated to the algorithm to maintain the diversity in the population.

Literature review

A methodology based on branch and bound (B&B), which is considered to be an exact method, has been proposed by Arthanari and Ramamurthy (1971) to solve FFSP. Carlier and Neron (2000) have applied B&B to solve 77 benchmark problems of FFSP. Lower bound for makespan proposed by Santos et al. (1995) can be used as a measure to find the efficiency of the algorithms. To minimize makespan and flow time, Brah and Loo (1999) have proposed several heuristics (previously applied to FSP) to solve FFSP. A regression analysis is proposed to study the effect of problem characteristics on performance of heuristics. Ruiz et al. (2008) have conducted tests on several dispatching rules on realistic FFSP. Results show that modified NEH (Nawaz, Enscore, Ham) heuristic proposed by Nawaz et al. (1983) outperform all other heuristics. Ying and Lin (2009) have proposed an efficient heuristic called the heuristic of multistage hybrid flow shop (HMHF) to solve FFSP with multi-processor tasks. Kahraman et al. (2010) have proposed a parallel greedy algorithm (PGA) to solve FFSP with multi-processor tasks with four constructive heuristic techniques that were used to develop the PGA.

Initially, the mostly used meta-heuristic is GA for solving FFSP with an objective to minimize makespan (Ulusoy 2004; Oguz and Ercan 2005; Ruiz and Maroto 2006; Kahraman et al. 2008; Shiau et al. 2008; Urlings et al. 2010; Engin et al. 2011). Artificial immune system (AIS), which uses the affinity maturation mechanism and clonal selection principle, has been successfully applied by Engin and Doyen (2004) to solve FFSP. With the inspiration from natural phenomenon of ant colony, ant colony optimization (ACO) has been applied by Ying and Lin (2006) to solve FFSP. Alaykyran et al. (2007) have conducted a parametric study on the application of ACO to FFSP and proposed an improved ACO. Niu et al. (2009) have proposed a quantum-inspired immune algorithm (QIA), a hybrid algorithm inspired from quantum algorithm (QA) and immune algorithm (IA), for solving 41 FFSP from Carlier and Neron (2000) instances. Results indicate that QIA is superior to QA and IA. Wang et al. (2011) have proposed SA technique to solve FFSP with multi-processor tasks with an aim to minimize makespan. They have used three different decoding techniques (list scheduling, permutation scheduling, and first-fit method) and a local search technique to SA to obtain makespan. Mousavi et al. (2013) have proposed SA local search technique to minimize combined total tardiness and makespan for FFSP. Choong et al. (2011) have hybridized PSO with SA and TS techniques and proposed two hybrid PSO algorithms to solve FFSP. Liao et al. (2012) have proposed PSO hybridized with bottleneck heuristic to exploit the bottleneck stage and incorporated SA technique to avoid trapping at the local optima followed by a local search technique to improve the solution quality. Singh and Mahapatra (2012) have proposed PSO to solve FFSP using chaotic numbers generated from logistic mapping function instead of random numbers. Based on the features of integrated greedy algorithms and artificial immune system (AIS), Ying (2012) has proposed a new hybrid immune algorithm (HIA) to solve multistage FFSP with makespan as the objective. Chou (2013) has proposed a cocktail decoding method capable of improving the solution quality of any algorithm incorporated with PSO for solving FFSP with multi-processor tasks. An improved cuckoo search algorithm has been proposed by Marichelvam et al. (2014) to solve multi-stage FFSP. To obtain the near-optimal solutions rapidly using cuckoo search, initial solutions are generated with NEH heuristic. Cui and Gu (2015) have proposed an improved discrete artificial bee colony (IDABC) algorithm to solve FFSP. The IDABC uses a combination of modified variable neighbourhood search (VNS) and differential evolution (DE) techniques to generate new solutions. A modified harmony search approach using smallest position value (SPV) rule is applied to solve multi-stage FFSP with an aim to minimize makespan by Marichelvam and Geetha (2016). For critical analysis of FFSP problems, Ribas et al. (2010) have presented a literature review on exact, heuristic and meta-heuristics methods proposed to solving FFSP. Careful analysis of literature on FFSP reveals that meta-heuristic approaches are widely used for improving solution quality. However, any algorithm or its hybridisation variant needs tuning of algorithm-specific parameters to obtain good solutions. An algorithm that does not require algorithm-specific parameters to be tuned may be another way of generating solution quality because it may reduce the burden of computation of tuning the algorithm for each problem instance. A brief description of the FFSP and its formulation is given in the next section.

Problem description and formulation

FFSP, commonly known as hybrid flow shop problem, has M jobs with ‘g’ number of operations to be carried out in ‘g’ stages. Each job n (n = 1, 2, …, M) is to be sequentially processed at each stage t (t = 1, 2,…, g). Each stage t (t = 1, 2,…, g) have MTt identical machines. At least one stage will have more than one machine and only one operation is carried out in each stage. The parallel machines in a stage are identical and take same time to process an operation. At any given time, a machine can process only one job. The processing time of each job m at a stage t ‘‘p (n, t)’’ is deterministic and it is known in advance. The objective is to find permutation of all jobs at each stage to reduce the makespan. The arrows in the Fig. 1 indicate the possible ways that a job can be processed from one stage to another. There are few assumptions (Marichelvam et al. 2014) involved in solving this problem. They are:

Fig. 1
figure 1

Schematic flow diagram of FFSP

Full size image

  • The number of machines at each stage and the number of stages are known in advance.

  • The processing times of jobs on these machines are deterministic and are known in advance.

  • There is no preemption during the process.

  • The transportation times and setup times of jobs are included in the processing times.

  • At a time, a machine can process only one job.

  • There is no machine breakdown or any other disturbance during the process.

The notations used are as follows:

\(n\) :

Number of jobs \((n = 1, 2, \ldots ., M)\)

\(g\) :

Number of stages \((t = 1, 2, \ldots , g)\)

\(MTt\) :

Total number of machines at stage \(t, (t = 1, 2, \ldots , g)\)

\(Jkt\) :

Jobs that are processed on machine k at stage t

\(Pntk\) :

Processing time of job n at stage t on machine k

\(Cntk\) :

Completion time of job n at stage t on machine k

\(Sntk\) :

Starting time of job n at stage t on machine k

\(Yntk\) :

 = 1 if job n is processed at stage t on machine k. 0, otherwise

\(htk\) :

Job h is processed at stage t on machine k. \(h = 1,2, \ldots \ldots , MTt\)

The mathematical model of FFSP is as explained below.

The objective is to minimize makespan (\(C_{ \hbox{max} }\)):

$$C_{\hbox{max} } \ge Cng \quad \forall n.$$
(1)

Subject to constraints

$$\mathop \sum \limits_{k = 1}^{MTt} Yntk = 1, \quad n = 1,2, \ldots , M;\;\quad t = 1,2, \ldots ,g,$$
(2)
$$\mathop \sum \limits_{k = 1}^{MTt} Jkt = n, \quad \forall t \in g,$$
(3)
$$Cntk \le Sn\left( {t + 1} \right)r, \quad\forall t \in g, \forall r \in MTt,$$
(4)
$$Cntk = Sntk + Pntk \quad\forall n,t,k,$$
(5)
$$Chtk \le S\left( {h + 1} \right)tk\quad \forall t,k,h,$$
(6)
$$C_{\hbox{max} } \ge Cng \quad\forall n,$$
(7)

Inequality (1) determines the makespan. Constraint (2) governs the assignment of each job at every stage. Constraint (3) assures that the total number of jobs assigned in a stage is equal to n. Constraint (4) ensures that a job cannot be processed in a later stage unless it is completely processed on the current stage. Constraint (5) determines the completion time of a job at a given stage. Constraint (6) determines that a machine cannot process next job unless it processes the current job completely. Constraint (7) determines that the makespan of a schedule should be always greater than or equal to completion time of all jobs at the last stage.

The problem is classified as NP-hard problem (Gupta 1988). The computation time increases exponentially if the size of the problem increases. Therefore, exact solution hardly gives a good solution in reasonable time. The researchers tend to use various meta-heuristic approaches to solve such type of problems. But turning of algorithm-specific parameter is really difficult to attain quality solutions. Hence, TLBO and JAYA algorithms which do not have any algorithm-specific tuning parameters are chosen for the study to evaluate their performance.

Teaching–learning-based optimization

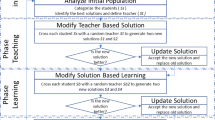
TLBO is proposed by Rao et al. (2011) with an inspiration from the general teaching–learning process how a teacher influence the knowledge of students. Students and teacher are the two main objects of a class and the algorithm explains the two modes of learning, i.e. via teacher (teacher phase) and discussion among the fellow students (student phase). A group of students of the class constitute the population of the algorithm. In any iteration ‘i’, the best student of the class becomes the teacher. Execution of the TLBO is explained in two phases, such as teacher phase and student phase.

Teacher phase

A teacher puts his/her best to increase the knowledge of his/her students to his level. But practically it is not possible as learning by a student depends on his/her potential to learn. In this process, each student’s knowledge increases and in turn the average knowledge of the class increases. At any iteration ‘i’, let Z mean denote the mean knowledge of the class and teacher of the class is denoted as Z teacher. Then increased knowledge of a student is given by the expression:

$$Z_{{{\text{new }}i}} = \, Z_{{{\text{old }}i}} \; + \; \, r\; \times \;\left( {Z_{\text{teacher}} {-} \, \left( {T_{\text{f}} \; \times \; \, Z_{\text{mean}} } \right)} \right),$$
(8)

where r is a random number between zero to one and T f is called teaching factor whose value is randomly chosen as one or two, and there is no tuning of this teaching factor even though T f is an algorithm-specific parameter of TLBO. Z new i is the new knowledge of the student ‘i’ after learning from the teacher. Z old i is the previous knowledge of the student ‘i’. Accept Z new i if it gives a better functional value.

Student phase

After a class is taught, students discuss among themselves. In this process, the knowledge of all students increases. At any iteration ‘i’, let Z a and Z b be two students who discuss after the class, a ≠ b. Then increased knowledge of the student is given by the expression:

$$Z_{{{\text{new }}a}} = \, Z_{{{\text{old }}a}} \; + \; \, r_{i} \; \times \;\left( {Z_{a} - \, Z_{b} } \right)\;\;{\text{ if }}F\left( {Z_{a} } \right) \, <= \, F\left( {Z_{b} } \right),$$
(9)
$$Z_{{{\text{new }}a}} = \, Z_{{{\text{old }}a}} \; + \; \, r_{i} \times \, \left( {Z_{b} {-} \, Z_{a} } \right)\;{\text{ if }}F\left( {Z_{b} } \right)\; < \;F\left( {Z_{a} } \right).$$
(10)

Z new a is the new knowledge of the student ‘a’ after learning from the co-student ‘b’. Z old a is the previous knowledge of the student ‘a’. Accept Z new a if it gives a better function value. The pseudo code of proposed TLBO is given in Fig. 3.

JAYA algorithm

JAYA algorithm is proposed by Rao (2016). This algorithm is designed on the simple logic that any solution of the given population should always move towards the best solution and move away from the worst solution. The beauty of this algorithm is that it contains only one equation and it does not contain any algorithm-specific parameters to be tuned to get optimal solution, which makes it very easy to understand and uniquely different from any other meta-heuristics. As compared to TLBO, JAYA has only one phase.

The mathematical description of JAYA algorithm is as follows. Let f(x) be the objective function to be optimized. At any iteration ‘i’, let Z best and Z worst denote the best and worst solutions, respectively, among the population, then a solution of the population is modified as follows:

$$Z_{{{\text{new }}i}} = \, Z_{{{\text{old }}i}} + \, r_{ 1} \times \, \left( {Z_{\text{best}} - \, | \, Z_{i} |} \right)\;{-}\;r_{ 2} \times \, \left( {Z_{\text{worst}} \; - \;| \, Z_{i} |} \right),$$
(11)

where r 1 and r 2 are the two random numbers between zero and one. The term r 1 × (Z best−|Z i |) denotes the nature of solution to move towards the best solution and the term −r2 × (Z worst−|Z i |) denotes the nature of the solution to move away from the worst solution. The new solution is accepted if it gives a better value. The flow chart of JAYA algorithm is given in Fig. 2. The pseudo code of proposed JAYA algorithm is given in Fig. 3.

Fig. 2
figure 2

Flow chart of Jaya algorithm

Full size image
Fig. 3
figure 3

Pseudo codes for proposed algorithms

Full size image

Although the TLBO and JAYA algorithms seem to be elegant, they lose solution diversity after few iterations and get trapped at the local optima. To alleviate such drawback, a new local search procedure is proposed in this paper to improve the solution quality. A brief description of the proposed local search is given in the next section of the paper as follows.

Local search

Literature suggests that researchers use local search techniques to improve the efficiency of meta-heuristics. For example, Wang et al. (2011) have used a local search technique to SA to improve solution quality. Choong et al. (2011) have embedded TS and SA to PSO separately to improve PSO efficiency. Liao et al. (2012) have used a local search technique to improve the efficiency of PSO. The present tuning parameter-less algorithms also require some improvements in the basic algorithm so that their efficiency may be improved in generating the optimal or near-optimal solutions. Although these algorithms seem to be elegant, they lose solution diversity after few iterations and may get trapped at the local optima. To overcome this drawback, a new local search technique is proposed in the present work to improve the solution quality of FFSP. This method is explained in two steps: (1) Sequence swap (2) machine swap.

Sequence swap

Before going to the sequence swap, all the critical operations of the schedule are to be found. Then two or more jobs that are allotted on the same machine adjacent to each other are picked and adjacent swapping [pair exchange method used by Xia and Wu (2005) and Buddala and Mahapatra (2016)] will be done to check whether there is any improvement in the quality of solution. This technique is called sequence swap. If the swap gives a better makespan value, then old solution is replaced by the new solution.

Machine swap

In a FFSP problem, at least one stage will have more than one machine. There is a possibility that critical operations can be allotted to the same machine in a stage with multiple machines. In such condition if one of the jobs is transferred to other parallel machine of the same stage, then there is a possibility for makespan reduction. This is called machine swap technique. If this swap gives a better makespan value, then old solution is replaced by the new solution.

Even though the TLBO and JAYA algorithms converge quickly, it is observed that the population of these algorithms lose diversity and get trapped at the local optimum. Therefore, to maintain diversity in the population, mutation strategy from GA is incorporated to these algorithms with an inspiration from Singh and Mahapatra (2012). Sing and Mahapatra have incorporated mutation strategy to PSO to maintain the diversity in the population. The working of mutation strategy is as follows.

Mutation strategy

Even though the rate of convergence of both the TLBO and JAYA is good, it is observed that when these algorithms are directly applied to solve the FFSP, they show a good tendency to be struck at the local optimum due to lack of diversity in the population. Therefore, as the iterations proceed, all the populations get converged to a local optimum and there is no improvement in the solution there after. To avoid this drawback, mutation strategy from genetic algorithm is incorporated to each of these basic algorithms after the local search step. Singh and Mahapatra (2012) have applied this mutation strategy to PSO for solving FFSP. Mutation is defined as a sudden change that occurs in the genes of the offspring when compared to that of parent genes during the evolution process. Out of the total population, a fixed percentage of population will undergo mutation. In this case, the percentage is fixed to three percent. It is based on the computational experiments conducted and it is explained in Fig. 5 under results and discussion. This mutation technique is implemented only if there is no improvement in the best solution for every fixed number of iterations. In the present case, mutation is applied if no improvement is observed in five iterations. This technique prevents the population converging to the local optimum and directs the same to the global optimum. After the incorporation of mutation strategy, we observe a good improvement in the quality of results produced by these two algorithms.

Problem mapping mechanism

In this method, a real number encoding system is used to solve the FFSP where the integer part is used to assign the machine at each stage and the fractional part is used to sequence the jobs allotted on each machine. Let us consider an example with jobs (n = 4) and operations (g = 3), i.e. three stages. Stages one, two and three have three, two and one machines, respectively (m 1 = 3, m 2 = 2, m 3 = 1). We generate 12 (4 × 3) real numbers randomly as shown in second row of Fig. 4 by uniform distribution between [1, 1 + m(k)] for each stage. The processing times p(n, t) = \(\left( {\begin{array}{*{20}c} 4 & 6 & 2 \\ {\begin{array}{*{20}c} 2 \\ 7 \\ \end{array} } & {\begin{array}{*{20}c} 3 \\ 1 \\ \end{array} } & {\begin{array}{*{20}c} 5 \\ 2 \\ \end{array} } \\ 1 & 2 & 3 \\ \end{array} } \right)\). In stage 1, job 1 is allotted to machine 1, job 2 and job 4 are allotted to machine 2, and job 3 is allotted to machine 3. The method adopted here is that for stage one the jobs on same machine are sequenced in the increasing order of fractional values. So job 2 is followed by job 4 in stage 1 as fractional value of job 2 is less than that of job 4. For stages greater than one sequence, priority is given to the completion times of jobs in their previous stage. A job whose completion time is small in the previous stage is sequenced first in the current stage. In stage 2 machine 1, job 3 is followed by job 1 because completion time of job 1 in stage 1 is less than the job 3 in stage 1. If the completion times are same then a job is randomly chosen for sequencing.

Fig. 4
figure 4

Problem mapping mechanism and solution representation

Full size image

Results and discussion

To evaluate the effectiveness of TLBO and JAYA algorithms in solving FFSP, experiments have been conducted on 77 benchmark problems taken from Carlier and Neron (2000). All the problems have been solved and the results are compared with various algorithms, such as BB, PSO, GA, AIS, IDABC, IA, QA, and QIA, from the literature available. Experiments have been conducted using MATLAB software on a 4-GB ram i7 processor running at 3.40 GHz on windows 7 platform. The problem notation, for instance j15c10a1 from Table 1, means a 15-jobs 10-stages problem where j stands for number of jobs, c stands for number of stages, a stands for machine distribution structure and ‘1’ is the index of the problem. In the present work, the problem sizes vary from jobs 10× stages 5 to jobs 15× stages 10.

Table 1 Results of benchmark problems
Full size table

Experiments have been carried out for different percentage of mutation ranging one to five. It is observed that best results of most of the problems are obtained when the mutation probability is fixed to three percent. This is clear from Fig. 5a, b which shows the variation of results obtained to some of the difficult problems solved by varying the mutation percentage for TLBO and JAYA, respectively. In this mutation process, randomly three solutions from the population are picked and they are replaced by new randomly generated solutions. In this way, a diversity in the population is maintained before converging to the optimal solution.

Fig. 5
figure 5

a Result variation with mutation percentage for TLBO. b Result variation with mutation percentage for JAYA

Full size image

Exact methods such as B&B fail to produce best results for large size FFSP problems. Therefore, there is a need for alternative method to find the best result (least possible makespan) that can be obtained for a FFSP. The least possible makespan values are nothing but the lower bound (LB) values. Therefore, to solve this problem, Santos et al. (1995) derived a formula to find lower bound for FFSP. In the present work, the formula to calculate lower bound values is taken from Santos et al. (1995) and it is given in the Eq. 12. Also, it is well known that heuristic and meta-heuristics does not guarantee a best result all the time. Therefore, lower bounds are essential and are used for comparing the efficiency of different algorithms.

$${\text{LB}} = { \hbox{max} }\left[ {\hbox{max} \left\{ {\mathop \sum \limits_{t = 1}^{g} p(i, t)} \right\},{ \hbox{max} }\left\{ {\frac{1}{MT(t)}\left( { \mathop \sum \limits_{y = 1}^{{{\text{MT}}(t)}} {\text{LSA}}\left( {y,t} \right) + \mathop \sum \limits_{i = 1}^{n} p(i,t) + \mathop \sum \limits_{y = 1}^{{{\text{MT}}(t)}} {\text{RSA}}\left( {y,t} \right) } \right)} \right\}} \right].$$
(12)

In Eq. 12, \({\text{MT}}(t)\) is the total number of machines at stage t, \(p(i,t)\) is the processing time of job i at stage t, LSA is left side processing times arranged in ascending order for stages in left side and RSA is right side processing times arranged in ascending order for stages in right side. For more information regarding the derivation of the above formula, one may refer to Santos et al. (1995).

Since meta-heuristics are stochastic in nature, the performance of the proposed algorithms is carried out through ten times and best values obtained by these algorithms are tabulated in Table 1. In Table 1, C max stands for makespan and PD is the percentage deviation of the solution from the lower bound (LB) value. The second column in Table 1 gives the LB values calculated using Eq. 12. At the end of the Table 1, average percentage deviation (APD) of each algorithm to the problems is calculated. The formula to find PD and APD are given in Eqs. 13 and 14, respectively.

$${\text{PD}} = \frac{{C_{ \hbox{max} } - {\text{LB}}}}{\text{LB}}\; \times \;100,$$
(13)
$${\text{APD}} = \frac{{\mathop \sum \nolimits_{X = 1}^{N} {\text{PD}}(X)}}{N}.$$
(14)

In Eq. 14, N is the total number of problems available with results to an algorithm and X is the index of the problem. A comparison of computational times taken by different algorithms to reach its optimal solution is shown in Table 2. In Table 2, C max stands for makespan, T(s) denotes time in seconds, and a denotes that the algorithm could not reach its optimum in 1600 s. A comparison of the best and average makespan values obtained by TLBO and JAYA are shown in Table 3. In Table 3, C max stands for makeskpan.

Table 2 Computational times
Full size table
Table 3 Comparison of best and average makespan values
Full size table

A comparison of convergence rates for TLBO and JAYA are given in the following Figs. 6, 7, 8 and 9 (for few problems, first problem from each set), where blue line indicates JAYA and black line indicates TLBO algorithms, respectively. Results show that rate of convergence of TLBO to reach the optimal result is superior to JAYA.

Fig. 6
figure 6

Problem instance j10c5a2

Full size image
Fig. 7
figure 7

Problem instance j10c10a1

Full size image
Fig. 8
figure 8

Problem instance j15c5a1

Full size image
Fig. 9
figure 9

Problem instance j15c10a1

Full size image

Out of these 77 problems, only forty-one problems have been solved by IA, QA and QIA whose APD values for these 41 problems are 6.31, 8.23 and 3.9, respectively. The APD value of TLBO for these 41 problems is 2.47 whose value is superior to QA, IA and QIA, and hence outperformed these three algorithms. Also, TLBO (APD = 2.32) outperformed BB (APD = 4.14). The total APD (for 77) value of TLBO is 2.32 which is very much closer to APD values of remaining algorithms, such as PSO (APD = 2.03), AIS (APD = 2.3), GA (APD = 2.28) and IDABC (APD = 2.22). Thus, we can conclude that TLBO is also one of the best meta-heuristic techniques that can be applied to solve FFSP.

The APD value of JAYA for the forty-one problems solved by IA, QA and QIA is 3.5 which outperformed all these three QA (APD = 6.31), IA (APD = 8.23) and QIA (APD = 3.9) algorithms. JAYA’s total APD (for 77 problems) value is 3.63 which also outperformed BB (APD = 4.14). The remaining algorithms PSO (APD = 2.03), AIS (APD = 2.3), GA (APD = 2.28) and IDABC (APD = 2.22) are superior in APD to JAYA (APD = 3.63). Thus, we can conclude that JAYA is one of the competitive meta-heuristic techniques that can be applied to solve FFSP.

Conclusions

In case of application of meta-heuristics of solving NP-hard problems, tuning of algorithm-specific parameters is essential to obtain near-optimal solutions. The present research work focuses on the strength of “algorithm-specific tuning parameter-less algorithms” as tuning of the “algorithm-specific tuning parameters” is a difficult task. A problem needs to be solved again and again until the right tuning parameters are found for that problem. This further increases the computational burden. This paper discusses the problem of flexible flow shop scheduling problems with an objective to minimize makespan. To the best of our knowledge, all the meta-heuristic algorithms that were used to solve FFSP are either very complex or have algorithm-specific parameters to be tuned or a combination of both. Therefore, the present paper focuses on simple meta-heuristic techniques which do not have any algorithm-specific tuning parameters that can be used to solve NP-hard FFSP problem. TLBO and JAYA are selected for the study as they proved to be simple and efficient algorithms in the recent past. A new local search technique followed by mutation strategy borrowed from GA has been incorporated in these basic algorithms to improve the efficiency. The proposed TLBO and JAYA have been applied to conduct computational experiments on 77 benchmark problems of FFSP and the makespan results obtained by these algorithms are compared with all the other eight algorithms available in the literature. Makespan and APD results from the Table 1 show that TLBO is one of the efficient algorithms that can be applied to solve FFSP since it produces results comparable to best results suggested by other algorithms. It is also observed that TLBO outperforms many algorithms, such as QA, IA, QIA and BB, in solving FFSP. On the other hand, JAYA which is an easy and simple to understand having only one algorithm-specific equation has also outperformed some algorithms, such as QA, IA, QIA and BB. It also gives near-optimal makespan results to best algorithms available in the literature. Thus, it can be concluded that JAYA is one of the best competitive meta-heuristic technique that can be applied to solve FFSP.

This paper encourages the future researchers to focus on “algorithm-specific tuning parameter-less algorithms” that can be applied to solve FFSP. As finding the right tuning parameters is a difficult task, this drawback can be addressed using the algorithm-specific tuning parameter-less algorithms, such as TLBO and JAYA. The present study can be extended to hybridize TLBO and JAYA with other algorithms in the future. The study can also be extended considering different uncertainties, such as machine breakdown and variable processing times in future.