A new approach for Robot selection in manufacturing using the ellipsoid algorithm

Abstract

The choice of suitable robots in manufacturing, to improve product quality and to increase productivity, is a complicated decision due to the increase in robot manufacturers and configurations. In this article, a novel approach is proposed to choose among alternatives, differently assessed by decision makers on different criteria, to make the final evaluation for decision-making. The approach is based on the ellipsoid algorithm for systems of linear inequalities. Most of the ranking methods depend on integration that becomes complicated for nonlinear membership functions, which is the case in robot selection. The method simply uses the membership function or its derivative. It takes the decision maker’s attitude in ranking. It effectively ranks fuzzy numbers and their images, preserving symmetry. It is a simple recursive algebraic formula that can be easily programmed. The performance of the algorithm is compared with the performance of some existing methods through several numerical examples to illustrate its advantages in ranking, and a robot selection problem is solved.

Introduction

The wide use of robot automation in the industry creates new challenges in the development of robot control and in the preferred choice among robots performing the same task. The choice of suitable robots is a complicated decision due to the large increase in robot manufacturers, configurations, and available options. Based on the evaluation of multiple conflicting criteria, the multicriteria decision-making (MCDM) provides an effective framework for choice (Rashid et al. 2014). MCDM is the process of finding the optimal alternative from all possible alternatives according to some criteria or attributes (Garg 2017b).

Due to the ambiguity and vagueness in the information resulting from human judgment and preference and the use of linguistic assessments instead of numerical values, the theory of fuzzy sets and its corresponding extensions, e.g., intuitionistic fuzzy sets and type-2 fuzzy sets, are applied in decision-making (Singh and Garg 2017). Fuzzy set theory is considered as a useful tool, especially when dealing with complex systems, where the interactions of the system’s variables are too complex to be precisely specified (Garg 2016d).

Fuzzy numbers attracted researchers and many studies were introduced. Fuzzy sets, later named type-1 fuzzy sets to distinguish them from various types introduced, have a crisp membership function value in the interval [0, 1]. In some cases, it is hard to estimate the exact membership function of fuzzy sets. Therefore, type-2 fuzzy sets were introduced having a fuzzy membership function. However, type-2 fuzzy sets need heavy computations. Thus, interval type-2 fuzzy sets were proposed according to certain simplification assumptions (Ghorabaee 2016).

In practical applications, when evaluating some candidate alternatives, decision makers may fail to express their preference accurately due to insufficient knowledge of the alternatives. This led to the introduction of intuitionistic fuzzy sets (Garg 2016a). They are characterized by defining a degree of membership and a degree of nonmembership such that their sum is less than or equal to one (Garg 2017a). If the decision maker provides the sum of the membership degree and the nonmembership degree, of a certain attribute, greater than 1, the concept of Pythagorean fuzzy sets (a generalization of intuitionistic fuzzy sets) may be used under the assumption that the sum of the squares of the membership degree and the nonmembership degree is less than or equal to 1 (Garg 2016c). To improve the flexibility of intuitionistic fuzzy sets, interval-valued intuitionistic fuzzy sets were proposed having an interval membership function, an interval nonmembership function, and an interval hesitancy function (Garg 2016b).

When the information is indeterminate and inconsistent, fuzzy sets and their extensions are not appropriate for decision-making. To deal with such cases, neutrosophic sets were proposed. They have three independent components lying in $]0^{ + } , 1^{ + } [$: the truth degree, indeterminacy degree, and falsity degree (Nancy and Garg 2016).

For details on the application of interval type-2 fuzzy numbers in decision-making, see Ghorabaee (2016) and Demova et al. (2015). For the applications of intuitionistic fuzzy sets, see Garg (2016a, b, c, 2017a, b, c) and Singh and Garg (2017), and for neutrosophic sets, see Nancy and Garg (2016).

Comparing or ranking fuzzy numbers plays a crucial role in fuzzy decision problems, e.g., the concept of optimal or best choice is based on ranking. The main difficulty in ranking fuzzy numbers is that fuzzy numbers do not always yield a totally ordered set as real numbers do (Yoon 1996). To rank fuzzy numbers, a fuzzy number needs to be evaluated and compared to other fuzzy numbers. Since fuzzy numbers are represented by possibility distributions, they may overlap with each other. Thus, to decide whether one fuzzy number is bigger than or smaller than the other is difficult (Shureshjani and Darehmiraki 2013).

The importance of ranking fuzzy numbers in solving real world decision problems in a fuzzy environment led to the development of various ranking approaches. Diverse ranking methods have been proposed based on different theoretical basis. Accordingly, different ranking methods may propose different rankings (Brunelli and Mezei 2013). The existing ranking methods are classified into four categories each category has several methods (Chen and Chen 2009): preference relation (degree of optimality, hamming distance, α-cut, comparison function, desirability index), fuzzy mean and spread (probability distribution), fuzzy scoring (proportion to optimal, left/right scoring, centroid index, area measurement) and linguistic expression (intuition, linguistic approximation). For details on different ranking methods and a comparative study, see Brunelli and Mezei (2013). For recent research on ranking trapezoidal fuzzy numbers based on the shadow length and ranking triangular fuzzy numbers by pareto approach on two dominance stages, see Chutia et al. (2015).

Most of these methods suffer from several flaws, some are computationally complex or difficult to implement, and some are not discriminating, while others occasionally conflict with intuition (Sharma 2015). Many existing methods for ranking fuzzy numbers are neutral; they do not reflect the decision maker’s subjective attitude in the process of ranking. To overcome this limitation, Shureshjani and Darehmiraki (2013) introduced an approach for ranking fuzzy numbers based on α-cuts representing the decision maker’s preference information explicitly. Since almost each method has a certain drawback, still none of the existing ranking methods is superior to the others (Sharma 2015).

The ellipsoid method has long been used in convex optimization, and proved to be extremely robust and efficient (Ecker and Kupferschmid 1985), but has not been applied to MCDM. This article investigates the usage of the ellipsoid method for systems of linear inequalities to rank normal and non-normal fuzzy numbers of equal heights and its application in robot selection. The area enclosed by the fuzzy number will be dealt with as the solution set of a system of linear inequalities, where the membership functions represent the constraints. For fuzzy numbers, the ellipsoid reduces simply to an ellipse. The method can effectively rank various fuzzy numbers and their images, whether the membership function is linear or nonlinear. Most of the ranking methods depend on integration, e.g., the centroid, the radius of gyration, the mean of removals, which becomes more elaborate when dealing with nonlinear membership functions. On the contrary, the ellipsoid method uses the membership function directly if it is linear and uses its derivative if it is nonlinear. It is a simple recursive algebraic formula that can be easily implemented. The method can take the decision maker’s attitude in ranking. It is also shown that it has a significant impact when ranking overlapping fuzzy numbers.

The article is organized as follows. Fuzzy numbers are defined in Sect. 2. The ellipsoid method is presented in Sect. 3. Section 4 explains setting the area enclosed by the fuzzy number as a system of linear inequalities. The proposed method is given in Sect. 5. Comparative examples are given in Sect. 6. The robot selection problem is solved using the proposed method in Sect. 7. The findings are discussed in Sect. 8. Finally, the conclusion is given in Sect. 9.

Preliminaries

Fuzzy numbers are a special kind of fuzzy sets that are normal and convex (Yoon 1996). They are defined in various ways using many types of shapes. The most salient types of fuzzy numbers in practical applications are the trapezoidal and triangular fuzzy numbers. They are defined as follows:

Definition 2.1

(Chu and Tsao 2002) A real fuzzy number $\tilde{A}$ is a fuzzy subset of the real line R with membership function $f_{{\tilde{A}}}$ having the following properties:

• (a) $f_{{\tilde{A}}}$ is a continuous mapping from R to the closed interval $\left[ {0,\omega } \right], 0 \le \omega \le 1;$

• (b) $f_{{\tilde{A}}} (x) = 0, {\text{for all }} x \in \left( { - \infty ,a_{1} } \right];$

• (c) $f_{{\tilde{A}}}$ is strictly increasing on $\left[ {a_{1} ,a_{2} } \right];$

• (d) $f_{{\tilde{A}}} \left( x \right) = \omega , {\text{for all }} x \in [a_{2} ,a_{3} ];$ where ω is constant and $0 < \omega \le 1$

• (e) $f_{{\tilde{A}}}$ is strictly decreasing on $\left[ {a_{3} ,a_{4} } \right];$

• (f) $f_{{\tilde{A}}} \left( x \right) = 0, {\text{for all }} x \in [a_{4} ,\infty );$

where a ₁, a ₂, a ₃, and a ₄ $\in R$. It is assumed that $\tilde{A}$ is convex and bounded unless otherwise stated. If ω $= 1, \tilde{A}$ is called a normal fuzzy number; otherwise it is called a non-normal fuzzy number.

Definition 2.2

(Chu and Tsao 2002) The membership function of a fuzzy number $\tilde{A} = [a_{1} , a_{2} , a_{3} , a_{4} ;\omega ]$ is expressed by

$$f_{{\tilde{A}}} \left( x \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {f_{{\tilde{A}}}^{L} ,} & {a_{1} \le x \le a_{2} ,} \\ \end{array} } \\ {\begin{array}{*{20}c} {\omega ,} & { a_{2} \le x \le a_{3} } \\ \end{array} ,} \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {f_{{\tilde{A}}}^{R} ,} & {a_{3} \le x \le a_{4} } \\ \end{array} ,} \\ {\begin{array}{*{20}c} {0,} & { {\text{otherwise}}} \\ \end{array} ,} \\ \end{array} } \\ \end{array} } \right.$$

where $f_{{\tilde{A}}}^{L}$ and $f_{{\tilde{A}}}^{R}$ are the left and right membership functions respectively, and $0 < \omega \le 1$. $f_{{\tilde{A}}}^{L} :\left[ {a_{1} ,a_{2} } \right] \to \left[ {0,\omega } \right]$ is a continuous mapping from the real line R to the closed interval $\left[ {0,\omega } \right]$, and it is strictly increasing on the interval $\left[ {a_{1} ,a_{2} } \right].$ Similarly, $f_{{\tilde{A}}}^{R} :\left[ {a_{3} ,a_{4} } \right] \to \left[ {0,\omega } \right]$ is a continuous mapping from the real line R to the closed interval $\left[ {0,\omega } \right],$ and it is strictly decreasing on the interval $\left[ {a_{3} ,a_{4} } \right].$ The inverse functions of both the left and right membership functions exist and are denoted by $g_{{\tilde{A}}}^{L} {\text{ and }} g_{{\tilde{A}}}^{R} ,$ respectively.

If $f_{{\tilde{A}}}^{L}$ and $f_{{\tilde{A}}}^{R}$ are both linear, $\tilde{A}$ is named as a trapezoidal fuzzy number, and is usually denoted by $\tilde{A} = (a_{1} , a_{2} , a_{3} , a_{4} ;\omega ).$ When $\omega = 1,$ the fuzzy number is simply denoted by $\tilde{A} = (a_{1} , a_{2} , a_{3} , a_{4} ).$ Else, if the function is nonlinear it is named according to the type of function, e.g., exponential trapezoidal fuzzy number. If $a_{2} = a_{3}$, a trapezoidal fuzzy number reduces to a triangular fuzzy number denoted by $\tilde{A} = (a_{1} , a_{2} , a_{3} ;\omega )$ or $\tilde{A} = (a_{1} , a_{2} , a_{3} )$ for $\omega = 1$.

Definition 2.3

(Chu and Lin 2009) The α-cuts of a fuzzy number $\tilde{A}$ are given by $\tilde{A}^{\alpha } = \left\{ {x:f_{{\tilde{A}}} \left( x \right) \ge \alpha } \right\},$ $\alpha \in \left[ {0, 1} \right],$ where $\tilde{A}^{\alpha }$ is a nonempty bounded closed interval in R. The crisp set $\tilde{A}^{\alpha }$ is denoted by $\tilde{A}^{\alpha } = [\tilde{A}_{l}^{\alpha } ,\tilde{A}_{u}^{\alpha } ],$ where $\tilde{A}_{l}^{\alpha }$ is the lower bound and $\tilde{A}_{u}^{\alpha }$ is the upper bound.

If “α” is close to 1, the pertaining decision is referred to as a “high-level decision”. Meanwhile, if “α” is close to 0, the pertaining decision is referred to as a “low-level decision”.

Using interval arithmetic some basic operations on the fuzzy numbers $\tilde{A}\; {\text{and}}\; \, \tilde{B} \in R^{ + }$ with α-cuts $\tilde{A}^{\alpha } = \left[ {\tilde{A}_{l}^{\alpha } ,\tilde{A}_{u}^{\alpha } } \right] \;{\text{and}}\;\tilde{B}^{\alpha } = [\tilde{B}_{l}^{\alpha } ,\tilde{B}_{u}^{\alpha } ]$, are expressed as follows (Chu and Lin 2009):

$$\begin{aligned} (\tilde{A} \oplus \tilde{B})^{\alpha } = & \left[ {\tilde{A}_{l}^{\alpha } + \tilde{B}^{\alpha } ,\tilde{A}_{u}^{\alpha } + \tilde{B}_{u}^{\alpha } } \right], \\ (\tilde{A} \otimes \tilde{B})^{\alpha } = & \left[ {\tilde{A}_{l}^{\alpha } .\tilde{B}^{\alpha } ,\tilde{A}_{u}^{\alpha } .\tilde{B}_{u}^{\alpha } } \right], \\ {\text{and}}\;(\tilde{A} \otimes r)^{\alpha } = & \left[ {\tilde{A}_{l}^{\alpha } .r,\tilde{A}_{u}^{\alpha } .r} \right],\quad r \in R^{ + } . \\ \end{aligned}$$

The ellipsoid algorithm

Yudin and Nemirovski (1976) and Shor (1977) introduced the ellipsoid method as an iterative method for general convex optimization problems. Later, Khachiyan (1979) applied the method to linear programs to prove that they can be solved in polynomial time (Beck and Sabach 2012). However, the ellipsoid method proved to be more effective in decision problems than optimization problems (Rebennack 2008).

Consider the decision problem of finding a feasible point for the system of linear inequalities

$${\mathbf{Ax}} \le {\mathbf{b}},\quad {\text{where}}\quad {\mathbf{A}} \in R^{m \times n} ,\;{\mathbf{x}} \in R^{n} \quad {\text{and}}\quad {\mathbf{b}} \in R^{m} .$$

The basic idea of the algorithm is to start with an initial ellipsoid containing the solution set of the system of linear inequalities ${\mathbf{Ax}} \le {\mathbf{b}}$. In each step, the center of the ellipsoid is a candidate to be a feasible point of the problem. It is checked whether this point satisfies all the linear inequalities or not. If the point is feasible, then the algorithm terminates. Otherwise, this point violates one or more of the given inequalities. One of the violated constraints is used to construct a new ellipsoid of a smaller volume having a different center. The procedure is repeated until either a feasible point is obtained or the number of the carried out iterations implies that the system is infeasible.

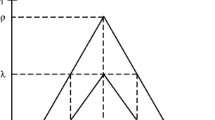
It’s worth noting the algorithm possesses a geometric property which can be used to rank fuzzy numbers. The ellipse generated in the $(k + 1)$ iteration,$E_{k + 1}$, is tangential to the ellipse in the kth iteration, $E_{k} ,$ and passes through the points of intersection of the cutting constraint and the kth ellipse as shown in Fig. 1a. Therefore, if two constraints can be used for cutting, the center of the ellipse generated by a leading constraint is in an advanced position as seen in Fig. 1a, b. This geometric property is exploited to rank fuzzy numbers.

Fig. 1

a Leading cut. b Lagging cut

In this study, the area enclosed by the fuzzy number will be dealt with as the solution set of a system of linear inequalities, where the membership functions represent the constraints. Therefore, the algorithm can be applied to rank fuzzy numbers, extending the conventional ellipsoid method to MCDM. The details will be given in Sect. 5.

Fuzzy numbers with linear inequalities

The membership function $y = f_{{\tilde{A}}} \left( x \right)$ is used to represent the area enclosed by the fuzzy number by a system of linear inequalities with the non-negativity condition as follows:

$$\begin{aligned} y - f_{{\tilde{A}}}^{L} (x) & \le 0, \\ y & \le \omega , \\ y - f_{{\tilde{A}}}^{R} (x) & \le 0 , \\ {\text{and}}\; y & \ge 0. \\ \end{aligned}$$

For a normal trapezoidal fuzzy number $\tilde{A} = (a_{1} , a_{2} , a_{3} , a_{4} )$ with a piecewise linear membership function defined by

$$f_{{\tilde{A}}} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{{x - a_{1} }}{{a_{2} - a_{1} }}} \hfill & {{\text{when}}\; a_{1} \le x < a_{2} ,} \hfill \\ 1 \hfill & {{\text{when}}\; a_{2} \le x \le a_{3} ,} \hfill \\ {\frac{{a_{4} - x}}{{a_{4} - a_{3} }}} \hfill & {{\text{when}}\; a_{3} < x \le a_{4} ,} \hfill \\ 0 \hfill & {{\text{otherwise}},} \hfill \\ \end{array} } \right.$$

the system of linear inequalities ${\mathbf{Ax}} \le {\mathbf{b}}$ is given by

$$\left( {\begin{array}{*{20}c} { - 1} & {a_{2} - a_{1} } \\ 0 & 1 \\ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {a_{4} - a_{3} } \\ { - 1} \\ \end{array} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) \le \left( {\begin{array}{*{20}c} { - a_{1} } \\ 1 \\ {\begin{array}{*{20}c} {a_{4} } \\ 0 \\ \end{array} } \\ \end{array} } \right).$$

For a triangular fuzzy number $\tilde{A} = (a_{1} , a_{2} , a_{3} )$ with a piecewise linear membership function defined by

$$f_{{\tilde{A}}} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{{x - a_{1} }}{{a_{2} - a_{1} }}} \hfill & {{\text{when}}\; a_{1} < x \le a_{2} ,} \hfill \\ {\frac{{a_{3} - x}}{{a_{3} - a_{2} }}} \hfill & {{\text{when}} \;a_{2} < x \le a_{3} ,} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$

the system of linear inequalities is given by

$$\left( {\begin{array}{*{20}c} { - 1} & {a_{2} - a_{1} } \\ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {a_{3} - a_{2} } \\ { - 1} \\ \end{array} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) \le \left( {\begin{array}{*{20}c} { - a_{1} } \\ {\begin{array}{*{20}c} {a_{3} } \\ 0 \\ \end{array} } \\ \end{array} } \right).$$

For the previous types of fuzzy numbers, if the membership function is a nonlinear function, it can be replaced by its tangent plane at the point $\left[ {x_{\alpha } ,\alpha } \right]$, where $x_{\alpha } = g_{{\tilde{A}}} (\alpha ).$ Then, the inequality representing the nonlinear function is given by

$$\left( {\begin{array}{*{20}c} { - f^{'} \left( {x_{\alpha } } \right)} & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) \le \left( {\alpha - x_{\alpha } f^{'} \left( {x_{\alpha } } \right)} \right).$$

The proposed method

Suppose $\tilde{A}_{i} ,i = 1, 2, \ldots , N$ are the N normal fuzzy numbers to be ranked, each having a membership function $f_{{\tilde{A}_{i} }} \left( x \right).$ Let $x_{\hbox{min} } = \inf X$ and $x_{\hbox{max} } = \sup X,$ where

$$X = \mathop {\bigcup }\limits_{i = 1}^{N} x_{i} , x_{i} = \left\{ {x | f_{{\tilde{A}_{i} }} \left( x \right) > 0} \right\}.$$

An ellipse with center ${\mathbf{x}}_{c}$ is formulated algebraically as the set $E\left( {{\mathbf{x}},{\mathbf{B}}} \right) = \left\{ {{\mathbf{x}}:\left( {{\mathbf{x}} - {\mathbf{x}}_{c} } \right)^{\text{T}} {\mathbf{B}}^{ - 1} \left( {{\mathbf{x}} - {\mathbf{x}}_{c} } \right) \le 1} \right\}$, where B is a symmetric, positive definite, and real valued 2 × 2 matrix. The eigenvectors of ${\mathbf{B}}$ define the principal axes of the ellipse, while the eigenvalues define the squares of the semi-axes $r_{x}$ and $r_{y} .$

A Starting ellipse $E_{o}$ is chosen large enough to contain the core of all the N fuzzy numbers, its center ${\mathbf{x}}_{c}$ and matrix B are given by

$${\mathbf{x}}_{c}^{o} = \left[ {\begin{array}{*{20}c} {x_{c}^{o} } & {y_{c}^{o} } \\ \end{array} } \right]^{\text{T}} \quad {\text{and}}\quad {\mathbf{B}} = \left( {\begin{array}{*{20}c} {r_{x}^{2} } & 0 \\ 0 & {r_{y}^{2} } \\ \end{array} } \right),$$

where $x_{c}^{o} = (x_{\hbox{min} } + x_{\hbox{max} } )/2$, $y_{c}^{o} = \omega /2$, $r_{x} = \left( {x_{\hbox{max} } - x_{\hbox{min} } } \right)/2$, and $r_{y} = \omega /2$.

Starting from $E_{o}$, the following procedure is applied to each fuzzy number $\tilde{A}_{i}$ to construct N smaller ellipses one for each fuzzy number. In each iteration, it is checked whether the current ellipse center ${\mathbf{x}}_{c}^{k}$ satisfies the inequalities $y - f_{{\tilde{A}}}^{L} \left( x \right) \le 0$ and $y - f_{{\tilde{A}}}^{R} (x) \le 0.$ If one of them is violated, it is used to cut the ellipse into two parts. One part does not contain any part of the fuzzy set, while the other part encloses part of the set. If both of them are violated, the one with the deepest possible cut, i.e., the cut corresponding to the largest $\rho$, is chosen. Whenever the factor $\rho$ is the same for both cuts, the right inequality is used when $x_{c} \ge 0$, while the left inequality is used when $x_{c} < 0$.

A new ellipse $E_{k + 1}$, which is smaller in area than $E_{k}$ is generated enclosing the core of the fuzzy number. The updating formulas are given as follows (Bland et al. 1981):

$${\mathbf{x}}_{c}^{k + 1} = {\mathbf{x}}_{c}^{k} - \tau ({\mathbf{B}}_{k} {\mathbf{A}}_{m}^{\text{T}} )/\sqrt {\left( {{\mathbf{A}}_{m} {\mathbf{B}}_{k} {\mathbf{A}}_{m}^{\text{T}} } \right)} ,$$

(1)

$${\mathbf{B}}_{k + 1} = \delta \left( {{\mathbf{B}}_{k} - \sigma \left( {{\mathbf{B}}_{k} {\mathbf{A}}_{m}^{\text{T}} } \right)\left( {{\mathbf{B}}_{k} {\mathbf{A}}_{m}^{\text{T}} } \right)^{\text{T}} /\left( {{\mathbf{A}}_{m} {\mathbf{B}}_{k} {\mathbf{A}}_{m}^{\text{T}} } \right)} \right),$$

(2)

where $\tau , \sigma \;{\text{and}}\; \delta$ are given by

$$\tau = \left( {1/3} \right)\left( {1 + 2\rho } \right), \quad \sigma = \left( {2/3} \right)((1 + 2\rho )/\left( {1 + \rho } \right)) ,\quad \delta = (4/3) \left( {1 - \rho^{2} } \right),$$

$${\text{where}}\quad \rho = ({\mathbf{A}}_{m} {\mathbf{x}}_{c}^{k} - {\mathbf{b}}_{m} )/\sqrt {{\mathbf{A}}_{m}^{\text{T}} {\mathbf{B}}_{k} {\mathbf{A}}_{m} }$$

(3)

$${\text{and}}\quad ( - 1/2) < \rho < 1.$$

(4)

As mentioned in Sect. 4, for fuzzy numbers with linear membership function ${\mathbf{A}}_{m}$ and ${\mathbf{b}}_{m}$ are given by ${\mathbf{A}}_{R} = \left[ {\begin{array}{*{20}c} 1 & {a_{3} - a_{2} } \\ \end{array} } \right] \;{\text{and}}\; {\mathbf{b}}_{R} = a_{3}$ for triangular fuzzy numbers; ${\mathbf{A}}_{R} = \left[ {\begin{array}{*{20}c} 1 & {a_{4} - a_{3} } \\ \end{array} } \right] \;{\text{and}}\; {\mathbf{b}}_{R} = a_{4}$ for trapezoidal fuzzy numbers, ${\mathbf{A}}_{L} = \left[ {\begin{array}{*{20}c} { - 1} & {a_{2} - a_{1} } \\ \end{array} } \right]$ and ${\mathbf{b}}_{L} = - a_{1}$. For nonlinear membership function they are replaced by ${\mathbf{A}}_{m} = \left[ {\begin{array}{*{20}c} { - f^{'} \left( {x_{\alpha } } \right)} & 1 \\ \end{array} } \right]$ and ${\mathbf{b}}_{m} = \alpha - x_{\alpha } f^{'} \left( {x_{\alpha } } \right).$

The procedure is repeated, if possible, to get an ellipse with a specified area reduction ratio. The reduction ratio is given by $= Ar(E_{k + 1} )/Ar \left( {E_{k} } \right) = \delta \sqrt {1 - \sigma } .$

Several researchers pointed out that ranking fuzzy numbers using both the value on the horizontal axis x, the degree of representative location, and the value on the vertical axis y, average height, often demean the importance of the value on the horizontal axis and makes the ranking order not consistent with intuitions. It gives the same degree of importance to x and y in ranking, while actually, they have different degrees of importance since the importance of x is higher than y (Wang and Lee 2008). It was also pointed out that ranking order differs with the decision level (Liou and Wang 1992; Shureshjani and Darehmiraki 2013). Therefore, the value $x_{c}$ of the center of the final ellipse is used for ranking, while the value of $y$ is used as the decision level at which the ranking is done.

The algorithm is geometrically interpreted as follows. The smaller ellipse $E_{k + 1}$ which is generated from the ellipse $E_{k}$ passes through the points of intersection of the ellipse $E_{k}$ with the line used as a cut. Thus, a fuzzy number with leading membership function(s) yields a leading ellipse whose center $x_{c}$ is greater than the center of a fuzzy number with lagging membership function(s) (see Fig. 2).

Fig. 2

Ranking using the ellipsoid method

If it is required to rank the fuzzy numbers at a high decision level in which only parts of the fuzzy numbers, with membership values between “α” and “1”, is considered. The center of $E_{\text{o}}$ is elevated taken as ${\mathbf{x}}_{c}^{o} = \left[ {\begin{array}{*{20}c} {(x_{\hbox{min} } + x_{\hbox{max} } )/2} & {(1 + \alpha )/2} \\ \end{array} } \right]^{T}$ keeping the same B matrix. For low decision levels, $\alpha < 0.5$, the center of the starting ellipse $E_{\text{o}}$ is lowered taken as ${\mathbf{x}}_{c}^{\text{o}} = \left[ {\begin{array}{*{20}c} {(x_{\hbox{min} } + x_{\hbox{max} } )/2} & \alpha \\ \end{array} } \right]^{\text{T}} .$ The B matrix is slightly enlarged in the direction of x, $r_{x} = 3\left( {x_{\hbox{max} } - x_{\hbox{min} } } \right)/4$, to make sure that the inequalities cut the ellipse since the fuzzy numbers are wider at low levels. This way the undesired decision levels of the fuzzy number is excluded.

Comparative examples

In this section, several numerical examples are given serving the following purposes: clarifying the idea of the method, testing its effectiveness in ranking especially at different decision levels and finally its ability to avoid some shortcomings in some previous ranking methods. The first three numerical examples are from Chen and Sanguansat (2011), example 4 is from Wang and Luo (2009), examples 5 and 6 are from Deng et al. (2006), while example 7 is due to Rezvani (2014). Finally, example 8 is from Singh (2015). All the fuzzy numbers in the examples are ranked at $\alpha = 0.5$ unless otherwise stated, and the reduction ratio used is 0.9.

Example 6.1

Consider the fuzzy numbers $\tilde{A}_{1} = (0.1, 0.2,0.4,0.5)$, $\tilde{A}_{2} = (1,1, 1,1)$ shown in Fig. 3. Several ranking methods cannot calculate the ranking score of crisp-valued fuzzy numbers (Chen and Sanguansat 2011). When representing a crisp value, say $x = a$, in the form of inequalities; it is replaced by $x \le a$ and $x \ge a$ which is changed to $- x \le - a$. As such, the ellipsoid method keeps the value of the crisp-valued fuzzy number. The obtained results are $C(\tilde{A}_{1} ) = \left[ {\begin{array}{*{20}c} {0.3351} & {0.4735} \\ \end{array} } \right]^{\text{T}}$, and $C(\tilde{A}_{2} ) = \left[ {\begin{array}{*{20}c} 1 & {0.5} \\ \end{array} } \right]^{\text{T}}$. Then $\tilde{A}_{2} > \tilde{A}_{1}$, which agrees with the ranking of Chen and Sanguansat (2011).

Fig. 3

Example 6.1

Example 6.2

Consider the fuzzy numbers $\tilde{A}_{1} = ( - 0.5, - 0.3, - 0.1)$, $\tilde{A}_{2} = (0.1, 0.3, 0.5)$ shown in Fig. 4. Cheng’s method (1998) gets unreasonable results when comparing positive and negative fuzzy numbers (Chen and Sanguansat 2011). Applying the proposed method the result is $C(\tilde{A}_{1} ) = \left[ {\begin{array}{*{20}c} { - 0.2811} & {0.4238} \\ \end{array} } \right]^{\text{T}}$, and $C(\tilde{A}_{2} ) = \left[ {\begin{array}{*{20}c} {0.2811} & {0.4238} \\ \end{array} } \right]^{\text{T}}$, then $\tilde{A}_{2} > \tilde{A}_{1} .$ It is clear from this example that the proposed method preserves the symmetry of a number and its image.

Fig. 4

Example 6.2

Example 6.3

Consider the fuzzy numbers $\tilde{A}_{1} = (0.3, 0.5, 1)$, $\tilde{A}_{2} = (0.1, 0.6, 0.8)$ shown in Fig. 5. The starting center ${\mathbf{x}}_{\text{c}}^{0} = \left[ {\begin{array}{*{20}c} {0.55} & {0.5} \\ \end{array} } \right]^{\text{T}}$. The result is $C(\tilde{A}_{1} ) = \left[ {\begin{array}{*{20}c} {0.6011} & {0.4874} \\ \end{array} } \right]^{\text{T}}$ and $C(\tilde{A}_{2} ) = \left[ {0\begin{array}{*{20}c} {.4989} & {0.4874} \\ \end{array} } \right]^{\text{T}}$, then $\tilde{A}_{1} > \tilde{A}_{2}$ which coincides with the ranking of several methods (Chen and Sanguansat 2011). A different ranking order is obtained taking $\alpha \ge 0.8$. Wang and Luo (2009) and Shureshjani and Darehmiraki (2013) pointed out the difference in ranking according to the decision level. Changing the starting center to ${\mathbf{x}}_{\text{c}}^{0} = \left[ {\begin{array}{*{20}c} {0.55} & {0.9} \\ \end{array} } \right]^{\text{T}}$, the result is $C(\tilde{A}_{1} ) = \left[ {\begin{array}{*{20}c} {0.5387} & {0.6262} \\ \end{array} } \right]^{\text{T}}$, and $C(\tilde{A}_{2} ) = \left[ {0\begin{array}{*{20}c} {.5613} & {0.6262} \\ \end{array} } \right]^{\text{T}}$ for $\tilde{A}_{2}$, then $\tilde{A}_{1} < \tilde{A}_{2}$.

Fig. 5

Example 6.3

Example 6.4

Consider the following fuzzy numbers:

$$\tilde{A}_{1} = (5.06,5.06,10),\quad \tilde{A}_{2} = (3.53, 6,8.47)\quad \tilde{A}_{3} = (2,6.94,6.94)$$

shown in Fig. 6. These three fuzzy numbers cannot be ranked by the method of maximizing set and minimizing set due to their equal total utilities (Wang and Luo 2009). Let ${\mathbf{x}}_{c}^{\text{o}} = \left[ {\begin{array}{*{20}c} 6 & {0.5} \\ \end{array} } \right]^{\text{T}}$ and ${\mathbf{B}} = \left( {\begin{array}{*{20}c} {16} & 0 \\ 0 & {0.25} \\ \end{array} } \right)$. The resulting centers are $C(\tilde{A}_{1} ) = \left[ {\begin{array}{*{20}c} {6.7065} & {0.5} \\ \end{array} } \right]^{\text{T}}$, $C(\tilde{A}_{2} ) = \left[ {\begin{array}{*{20}c} {5.4777} & {0.4798} \\ \end{array} } \right]^{\text{T}}$, and $C(\tilde{A}_{3} ) = \left[ {\begin{array}{*{20}c} {5.2933} & {0.5000} \\ \end{array} } \right]^{\text{T}} .$ Then $\tilde{A}_{3} < \tilde{A}_{2} < \tilde{A}_{1}$. This ranking is the same as the ranking of Wang and Luo (2009). While the ranking of Wang and Luo (2009) was not affected by the decision level, the proposed method revealed that this ranking order is valid for a low-level decision, i.e., $\alpha \le 0.5.$ Changing the starting center to $\left[ {\begin{array}{*{20}c} 6 & {0.9} \\ \end{array} } \right]^{\text{T}} ,$ the results are $C(\tilde{A}_{1} ) = \left[ {\begin{array}{*{20}c} {5.8542} & {0.6137} \\ \end{array} } \right]^{\text{T}}$, $C(\tilde{A}_{2} ) = \left[ {\begin{array}{*{20}c} {5.8680} & {0.6169} \\ \end{array} } \right]^{\text{T}}$, and $C(\tilde{A}_{3} ) = \left[ {\begin{array}{*{20}c} {6.1458} & {0.6137} \\ \end{array} } \right]^{\text{T}}$ for $\tilde{A}_{3}$. Then, for a high-level decision the order is $\tilde{A}_{1} < \tilde{A}_{2} < \tilde{A}_{3}$.

Fig. 6

Example 6.4

Example 6.5

Consider the triangular fuzzy numbers $\tilde{A}_{1} = \left( {0.2, 0.3, 0. 5} \right), \tilde{A}_{2} = \left( {0.17, 0.32, 0.58} \right)$ and $\tilde{A}_{3} = \left( {0.25, 0.4, 0.7} \right)$ shown in Fig. 7. The proposed method yields $C\left( {\tilde{A}_{1} } \right) = \left[ {\begin{array}{*{20}c} {0.3406} & {0.4095} \\ \end{array} } \right]^{\text{T}} ,$ $C\left( {\tilde{A}_{2} } \right) = \left[ {\begin{array}{*{20}c} {0.3638} & {0.4341} \\ \end{array} } \right]^{\text{T}}$ and $C\left( {\tilde{A}_{3} } \right) = \left[ {\begin{array}{*{20}c} {0.4162} & {0.4799} \\ \end{array} } \right]^{\text{T}}$. Accordingly, the ranking is $\tilde{A}_{1} < \tilde{A}_{2} < \tilde{A}_{3} .$ Taking the images of these fuzzy numbers, the resulting centers are $C\left( { - \tilde{A}_{1} } \right) = \left[ {\begin{array}{*{20}c} { - 0.3406} & {0.4095} \\ \end{array} } \right]^{\text{T}} , C\left( { - \tilde{A}_{2} } \right) = \left[ { - \begin{array}{*{20}c} {0.3638} & {0.4341} \\ \end{array} } \right]^{\text{T}}$ and $C\left( { - \tilde{A}_{3} } \right) = \left[ {\begin{array}{*{20}c} { - 0.4162} & {0.4799} \\ \end{array} } \right]^{\text{T}}$, producing the order $- \tilde{A}_{1} > - \tilde{A}_{2} > - \tilde{A}_{3}$ which copes with the logical inference.

Fig. 7

Example 6.5

Example 6.6

Consider the triangular fuzzy number $\tilde{A}_{1} = \left( {1, 2, 5} \right)$ and the general fuzzy number $\tilde{A}_{2}$, shown in Fig. 8, whose membership function is defined as

$$f_{{\tilde{A}_{2} }} = \left\{ {\begin{array}{*{20}l} {[1 - \left( {x - 2} \right)^{2} ]^{1/2} ,} \hfill & {1 \le x \le 2,} \hfill \\ {\left[ {1 - \frac{1}{4}\left( {x - 2} \right)^{2} } \right]^{1/2} ,} \hfill & {2 \le x \le 4,} \hfill \\ {0,} \hfill & {{\text{otherwise}}.} \hfill \\ \end{array} } \right.$$

Fig. 8

Example 6.6

Using the proposed method, the nonlinear membership function is replaced by the tangent planes at the point $\left[ {\begin{array}{*{20}c} {1.1340} & {0.5} \\ \end{array} } \right]$ for $f^{L}$ and at the point $\left[ {\begin{array}{*{20}c} {3.7321} & {0.5} \\ \end{array} } \right]$ for $f^{R} .$ The result is $C\left( {\tilde{A}_{1} } \right) = \left[ {\begin{array}{*{20}c} {2.6800} & {0.4400} \\ \end{array} } \right]^{\text{T}}$ and $C\left( {\tilde{A}_{2} } \right) = \left[ {\begin{array}{*{20}c} {2.8100} & {0.4863} \\ \end{array} } \right]^{\text{T}}$. The order is $\tilde{A}_{2} > \tilde{A}_{1}$. This is the same order as given by Deng et al. (2006). Ranking the numbers at a low decision level ($\alpha = 0.2$), the result is $C\left( {\tilde{A}_{1} } \right) = \left[ {\begin{array}{*{20}c} {2.8522} & {0.1877} \\ \end{array} } \right]^{\text{T}}$ and $\left( {\tilde{A}_{2} } \right) = \left[ {\begin{array}{*{20}c} {2.7204} & {0.1968} \\ \end{array} } \right]^{\text{T}}$. Then, the ranking $\tilde{A}_{1} > \tilde{A}_{2}$ which is the same ranking as given by Chu and Tsao (2002). Liou and Wang (1992) also produced different rankings according to the decision level. For an optimistic decision maker $\tilde{A}_{2} > \tilde{A}_{1}$; while for a moderate and pessimistic decision maker $\tilde{A}_{1} > \tilde{A}_{2}$ (Chu and Tsao 2002).

Example 6.7

Consider the exponential trapezoidal fuzzy numbers $\tilde{A}_{1} = \left( {0.1, 0.2,0.4,0.5} \right)$ and $\tilde{A}_{2} = (0.1,0.3,0.3,0.5)$ shown in Fig. 9, whose membership functions are defined by

$$f_{{\tilde{A}_{1} }} = \left\{ {\begin{array}{*{20}l} {e^{10x - 2} } \hfill & {0.1 \le x \le 0.2,} \hfill \\ 1 \hfill & {0.2 \le x \le 0.4,} \hfill \\ {e^{4 - 10x} } \hfill & {0.4 \le x \le 0.5,} \hfill \\ \end{array} } \right.\quad {\text{and}}\quad f_{{\tilde{A}2}} = \left\{ {\begin{array}{*{20}c} {e^{5x - 1.5} } & {0.1 \le x \le 0.3,} \\ {e^{ - 5x + 1.5} } & {0.3 \le x \le 0.5} \\ \end{array} .} \right.$$

Fig. 9

Example 6.7

The results are $C\left( {\tilde{A}_{1} } \right) = \left[ {\begin{array}{*{20}c} {0.3307} & {0.5383} \\ \end{array} } \right]^{\text{T}}$ and $\left( {\tilde{A}_{2} } \right) = \left[ {\begin{array}{*{20}c} {0.2991} & {0.4976} \\ \end{array} } \right]^{\text{T}}$, then $\tilde{A}_{1} > \tilde{A}_{2}$. This agrees with the result of Rezvani (2014).

Example 6.8

Consider the following fuzzy numbers:

$$\tilde{A}_{1} = ( - 0.1,0, 0.1;0.4),\quad \tilde{A}_{2} = ( - 0.2, - 0.1,0.1,0.2;0.4)$$

shown in Fig. 10. The methods of Cheng (1998) and Chu and Tsao (2002) are not applicable. The methods of Yager (1978) and Chen and Sanguansat (2011) give $\tilde{A}_{1} = \tilde{A}_{2}$ which is considered not intuitive (Singh 2015). Starting with ${\mathbf{x}}_{c}^{\text{o}} = \left[ {\begin{array}{*{20}c} 0 & {0.2} \\ \end{array} } \right]^{\text{T}}$. The results are $C\left( {\tilde{A}_{1} } \right) = \left[ {\begin{array}{*{20}c} {0.0135} & {0.1986} \\ \end{array} } \right]^{\text{T}}$ and $C\left( {\tilde{A}_{2} } \right) = \left[ {\begin{array}{*{20}c} {0.0529} & {0.2052} \\ \end{array} } \right]^{\text{T}}$. The ranking of the numbers is $\tilde{A}_{1} < \tilde{A}_{2}$, the same ranking as Singh (2015).

Fig. 10

Example 6.8

Robot selection

Robot selection has always been an important issue for manufacturing companies to improve product quality and to increase productivity. Prospective robot buyers must choose from several robots which are capable of performing a specific task. Robots are selected according to certain criteria. These criteria are either objective or subjective (Chu and Lin 2009). Objective criteria are defined in numerical terms, e.g., cost, load capacity and positioning accuracy. Subjective criteria have qualitative definitions, e.g., training, man–machine interface, and programming flexibility. Measures of subjective criteria may not be accurately defined by decision makers. Furthermore, the evaluation of robot suitability versus subjective criteria, and the weights of the criteria are usually expressed in linguistic terms.

In this section, the proposed method is used in the robot selection problem given by Liang and Wang (1993) and resolved later by Chu and Lin (2003) using a different approach. Liang and Wang (1993) used the maximizing and minimizing set for ranking, which might fail in ranking as shown in Example 6.4. It was also shown to be illogical (Chu and Lin 2003). Chu and Lin (2003) used the technique of order preference by similarity to an ideal solution (TOPSIS). TOPSIS avoids the complicated calculations of irregular fuzzy numbers by deffuzification, this leads to loss of information and doesn’t reflect the whole picture.

In the following example, the procedures to develop the membership function of the final fuzzy evaluation value for each alternative are due to Chu and Lin (2009).

A manufacturing company demands a robot to do a material-handling task. A committee of four decision makers $D_{1} ,D_{2} ,D_{3} , \;{\text{and}}\; D_{4}$ is formed to rate and select the most suitable robot from three robots $R_{1} ,R_{2} \; {\text{and}}\; R_{3}$ that passed the preliminary screening. Six selection criteria are considered:

• (a) Three subjective criteria: man machine interface ($C_{1}$), programming flexibility ($C_{2}$) and vendor’s service ($C_{3}$).

• (b) Three objective criteria: purchase cost ($C_{4}$), load capacity ($C_{5}$) and positioning accuracy ($C_{6}$).

The decision makers use two sets of linguistic terms for evaluating the importance of each criterion and to assess the rating of each robot under each subjective criterion; the weighting set $W = \{ {\text{VL}}, L, M, H, {\text{VH}}\}$ and the rating set $S = \{ {\text{VP}}, {\text{P}}, {\text{F}}, {\text{G}}, {\text{VG}}\}$. The linguistic terms of the weighting set are: ${\text{VL}} = {\text{very low}}\; (0, 0, 0.3)$,$L = {\text{low}} (0, 0.3, 0.5)$, $M = {\text{medium}}\; (0.2, 0.5, 0.8)$, $H = {\text{high}}\;(0.5, 0.7, 1)$ and ${\text{VH}} = {\text{very high}}\;(0.7, 1, 1)$. The linguistic terms of the rating set are: ${\text{VP}} = {\text{very poor}}\; (0, 0, 0.2)$, $P = {\text{poor}}\;(0, 0.2, 0.4)$, $F = {\text{fair}}\;(0.3, 0.5, 0.7)$, $G = {\text{good}}\;(0.6, 0.8, 1)$ and ${\text{VG}} = {\text{very good}}\;(0.8, 1, 1)$. The data of the problem can be found in details in Liang and Wang (1993) and Chu and Lin (2003).

The solution procedure is briefly described as follows (Chu and Lin 2009):

Step 1 :

Aggregate the importance weights.

Let $W_{tj} = \left( {a_{tj} ,b_{tj} ,c_{tj} } \right), {\text{for }} t = 1, \ldots 6 \;{\text{and}}\;j = 1, \ldots ,4$ be the weight assigned to criterion $C_{t}$ by decision maker $D_{j}$

$$W_{t} = \left( {1/4} \right) \otimes \left( {W_{t1} \oplus W_{t2} \oplus W_{t3} \oplus W_{t4} } \right) = (a_{t} ,b_{t} ,c_{t} );$$

where $a_{t} = (\sum\nolimits_{j = 1}^{4} {a_{tj} } )/4$, $b_{t} = (\sum\nolimits_{j = 1}^{4} {b_{tj} } )/4\;{\text{and}}\;c_{t} = (\sum\nolimits_{j = 1}^{n} {c_{tj} } )/4.$

$$W_{1} = \left( {0.6, 0.85, 1} \right), \quad W_{2} = \left( {0.525, 0.8, 0.95} \right), \quad W_{3} = \left( {0.1, 0.4, 0.65} \right),$$

$$W_{4} = \left( {0.15, 0.45, 0.725} \right),\quad W_{5} = \left( {0.65, 0.925, 1} \right), \quad W_{6} = \left( {0.6, 0.85, 1} \right).$$

Step 2 :

Aggregate the ratings of the alternatives under subjective criteria.

Let $R_{itj} = \left( {o_{itj} ,p_{itj} ,q_{itj} } \right)$ be the rating assigned to robot $R_{i}$ for the subjective criterion$C_{t}$ by decision maker $D_{j} , {\text{for }} i = 1, \ldots 3, t = 1, \ldots 3 \;{\text{and}}\; j = 1, \ldots ,4.$

$$R_{it} = \left( {1/4} \right) \otimes \left( {R_{it1} \oplus R_{it2} \oplus R_{it3} \oplus R_{it4} } \right) = (o_{it} ,p_{it} ,q_{it} );$$

where, $o_{it} = (\sum\nolimits_{j = 1}^{4} {o_{itj} } )/4$, $p_{it} = (\sum\nolimits_{j = 1}^{4} {p_{itj} } )/4\; {\text{and}}\; q_{it} = (\sum\nolimits_{j = 1}^{n} {q_{itj} } )/4.$

$$R_{11} = \left( {0.5, 0.7, 0.85} \right), \quad R_{12} = \left( {0.375, 0.575, 0.775} \right), \quad R_{13} = \left( {0.3750, 0.5750, 0.7750} \right),$$

$$R_{21} = \left( {0.45, 0.65, 0.85} \right),\quad R_{22} = \left( {0.625, 0.825, 0.925} \right),\quad R_{23} = \left( {0.575, 0.775, 0.925} \right),$$

$$R_{31} = (0.575, 0.775, 0.925),\quad R_{32} = \left( {0.575, 0.775, 0.925} \right),\quad R_{33} = \left( {0.65, 0.85, 1} \right).$$

Step 3 :

Normalize the objective criteria.

To make the values of the subjective and the objective criteria compatible; the values of the objective criteria, whether fuzzy or not, must be converted to dimensionless indices. Let $T_{it} = (g_{it} ,u_{it} ,v_{it} )$, ${\text{for }} i = 1, \ldots 3 \;{\text{and}}\; t = 3, \ldots 6$, represents the values assigned by the decision makers to the robot $R_{i}$ for objective criterion ${\text{C}}_{t}$. The objective criteria are classified to benefit (load capacity) and cost (purchase cost and positioning accuracy). The computation of the converted objective criteria $R_{it} = \left( {o_{it} ,p_{it} ,q_{it} } \right)$ differs according to the class of the objective criteria. For benefit criteria $o_{it} = g_{it} /v_{t}^{ + } ,p_{it} = u_{it} /v_{t}^{ + } \; {\text{and}}\; q_{it} = v_{it} /v_{t}^{ + }$, where $v_{t}^{ + } = \hbox{max} v_{it}$. While $o_{it} = g_{t}^{ - } /v_{it} ,p_{it} = g_{t}^{ - } /u_{it} \;{\text{and}}\; q_{it} = g_{t}^{ - } /g_{it}$, where $g_{t}^{ - } = {\text{min }}g_{it}$ for cost criteria.

$$R_{14} = (0.9122, 0.9247, 0.931), \quad R_{15} = (0.9327, 0.9615, 1), \quad R_{16} = (0.7857, 0.9167, 1),$$

$$R_{24} = \left( {0.9375, 0.9643, 0.9783} \right),\quad R_{25} = \left( {0.8462, 0.8654, 0.8942} \right),$$

$$R_{26} = (0.6111, 0.6875, 0.7333),$$

$$R_{34} = (0.9643, 0.9926, 1) , \quad R_{35} = (0.8365, 0.8654, 0.9135) ,$$

$$R_{36} = (0.5789, 0.6471, 0.6875).$$

Step 4 :

Calculate the final ratings.

$$\begin{aligned} S_{it} =\, & W_{t} \otimes R_{it} \\ =\, & \left[ {\left( {b_{t} - a_{t} } \right)\alpha + a_{t} ,(b_{t} - c_{t} } \right)\alpha + c_{t} ] \otimes \left[ {\left( {p_{it} - o_{it} } \right)\alpha + o_{it} ,(p_{it} - q_{it} } \right)\alpha + q_{it} ] \\ =\, & [\left( {b_{t} - a_{t} } \right)\left( {p_{it} - o_{it} } \right)\alpha^{2} + \{ a_{t} \left( {p_{it} - o_{it} } \right) + o_{it} \left( {b_{t} - a_{t} } \right)\} \alpha + a_{t} o_{it} , \\ & \ (b_{t} - c_{t} )\left( {p_{it} - q_{it} } \right)\alpha^{2} + \{ c_{t} (p_{it} - q_{it} ) + q_{it} (b_{t} - c_{t} )\} \alpha + c_{t} q_{it} ] \\ S_{i} =\, & (1/6)\mathop \sum \limits_{t = 1}^{6} W_{t} \otimes R_{it} = \left[ {I_{i1} \alpha^{2} + J_{i1} \alpha +\, Q_{i} ,I_{i2} \alpha^{2} + J_{i2} \alpha + Z_{i} } \right], \\ \end{aligned}$$

where $I_{i1} = (1/6)\sum\nolimits_{t = 1}^{6} {\left( {b_{t} - a_{t} } \right)} \left( {p_{it} - o_{it} } \right)$, $J_{i1} = (1/6)\sum\nolimits_{t = 1}^{6} {a_{t} } \left( {p_{it} - o_{it} } \right) + o_{it} \left( {b_{t} - a_{t} } \right)$, $I_{i2} = (1/6)\sum\nolimits_{t = 1}^{6} {(b_{t} - c_{t} )} \left( {p_{it} - q_{it} } \right)$, $J_{i2} = (1/6)\sum\nolimits_{t = 1}^{6} {c_{t} } (p_{it} - q_{it} ) + q_{it} (b_{t} - c_{t} )$, and $Q_{i} = (1/6)\sum\nolimits_{t = 1}^{6} {a_{t} } o_{it}$, $Y_{i} = (1/6)\sum\nolimits_{t = 1}^{6} {b_{t} } p_{it}$, $Z_{i} = (1/6)\sum\nolimits_{t = 1}^{6} {c_{t} } q_{it} .$

Step 5 :

Develop the membership function of each weighted rating.

The left and right membership functions $f_{{S_{i} }}^{L}$ and $f_{{S_{i} }}^{R}$ of $S_{i}$ can be obtained as

$$\begin{aligned} f_{{S_{i} }}^{L} = \left\{ { - J_{i1} + [J_{i1}^{2} + 4I_{i1} (x - Q_{i}) ]^{1/2} } \right\}/2I_{i1} ,\quad Q_{i} \le x \le Y_{i} , \hfill \\ f_{{S_{i} }}^{R} = \left\{ { - J_{i2} - [J_{i2}^{2} + 4I_{i2} (x - Z_{i}) ]^{1/2} } \right\}/2I_{i2} ,\quad Y_{i} \le x \le Z_{i} \hfill \\ \end{aligned}$$

Then, the membership functions of the three alternatives are given as follows. For the first robot,

$$\begin{aligned} f_{{S_{1} }}^{L} = \left\{ { - 0.2352 + [0.05522 + 0.1396(x - 0.2915)]^{1/2} } \right\}/0.0698,\quad 0.2915 \le x \le 0.5616, \hfill \\ f_{{S_{1} }}^{R} = \left\{ {0.2554 - [0.0652 + 0.0798(x - 0.7942)]^{1/2} } \right\}/0.0339, \quad 0.5616 \le x \le 0.7942 . \hfill \\ \end{aligned}$$

For the second robot,

$$\begin{aligned} f_{{S_{2} }}^{L} = \left\{ { - 0.2385 + [0.05688 + 0.1316(x - 0.2855)]^{1/2} } \right\}/0.0658,\quad 0.2855 \le x \le 0.5569, \hfill \\ f_{{S_{2} }}^{R} = \left\{ {0.2368 - [0.0561 + 0.0636(x - 0.7775)]^{1/2} } \right\}/0.0318,\quad 0.5569 \le x \le 0.7778. \hfill \\ \end{aligned}$$

For the third robot,

$$\begin{aligned} f_{{S_{3} }}^{L} = \left\{ { - 0.2450 + [0.0600 + 0.1324(x - 0.2913)]^{1/2} } \right\}/0.0662,\quad 0.2913 \le x \le 0.5693 , \hfill \\ f_{{S_{3} }}^{R} = \left\{ {0.2430 - [0.0590 + 0.0628(x - 0.7966)]^{1/2} } \right\}/0.0314,\quad 0.5693 \le x \le 0.7966. \hfill \\ \end{aligned}$$

Step 6 :

Rank.

Applying the proposed method for ranking after replacing the nonlinear membership functions by their tangent planes at the points $[x_{0.5} , 0.5]$, the following results are obtained: $C\left( {\tilde{S}_{1} } \right) = \left[ {\begin{array}{*{20}c} {0.5525} & {0.4882} \\ \end{array} } \right]$, $C\left( {\tilde{S}_{2} } \right) = \left[ {\begin{array}{*{20}c} {0.5312} & {0.4917} \\ \end{array} } \right]$ and $C\left( {\tilde{S}_{3} } \right) = \left[ {\begin{array}{*{20}c} {0.5548} & {0.4853} \\ \end{array} } \right]$. This makes the third robot $R_{3}$ the most suitable selection for the loading task. This result agrees with the result of Liang and Wang (1993) while it differs from the result of Chu and Lin (2003) TOPSIS that ranked $R_{1}$ as the best selection.

Discussion

The proposed algorithm proved to be robust, have a strong discriminating ability and never fails to rank. While some methods fail in ranking crisp-valued fuzzy numbers, e.g., Chu and Tsao method (2002), the algorithm can calculate the ranking score of crisp values. The algorithm could also rank fuzzy numbers that could not be ranked by the method of maximizing and minimizing set, i.e., fuzzy numbers having the same left, right and/or total utility (Wang and Luo 2009). In addition, it is not affected by the centroid like the distance method and the area method that fail in ranking fuzzy numbers having the same centroid (Deng et al. 2006).

Most of the extant methods are neutral and don’t reflect the decision maker’s preference in ranking. For example, the methods of Chu and Tsao (2002), Chen and Chen (2009) and Chen and Sanguansat (2011) ignore the decision level in ranking which is inconvenient in the case of intersecting fuzzy numbers that may differ in ranking according to the decision level (Shureshjani and Darehmiraki 2013). The proposed algorithm can simply take the decision level into consideration without using the traditional alpha cuts or the parametric form.

The proposed algorithm preserved symmetry and kept consistency in ranking fuzzy numbers and their images. In the methods proposed by Wang et al. (2009) and Asady (2010), the orders of the images were inconsistent (Sharma 2015).

Finally, the algorithm deals with the fuzzy numbers regardless being normalized or not, since some methods cannot rank fuzzy numbers unless being normalized, e.g., Chen and Sanguansat (2011).

Conclusion

In this article, the ellipsoid method was exploited to solve the robot selection problem by ranking various fuzzy alternatives. Most of the ranking methods use integration which needs more computations for fuzzy numbers with nonlinear membership functions. The main advantage of the proposed method is the usage of the linear membership functions directly, or the usage of the derivative of nonlinear membership functions. The method also preserves the symmetry between the fuzzy number and its image in defuzzification. The method can take the decision maker’s attitude in ranking. Several numerical examples were solved to test the proposed method. The method proved to be robust and effectively ranked various fuzzy numbers and their images, even if they are overlapping. It is a simple recursive algebraic formula that can be easily programmed.