Introduction

The purpose of this paper is to review some of the DLPs research which has contributed to the current state-of-the-art and fills the gap in the literature. The focus is on the classification of current mathematical models, solution methods and applications available in the literature. Our objective is to provide a survey of dynamic location problems in the different fields of facility location.

Selecting the best location of facilities or new facilities is an important function in time horizon. Before determining the place of facilities, the profitable locations should be selected, the capacity of it defined and amount of budget should be specific. Hence, high costs of this process is problematic for every location in regard to a long-term planning and investing. Regarding planning for future conditions and also large amount of budget that is needed to establish a facility, selecting a location should be in a way that the facility could be efficient and accessible in time horizon (Owen and Daskin 1998).

The strategic nature of facility location problems necessitate some aspect of future uncertainty to be considered in models. Due to the broader researches in location and relocation problems, decision makers selected the locations that can be effective for a time period, relocations over the long term, timing of facility expanded and changing demands that occur during the time simultaneously. Therefore, decision makers should select places that are not only ideal for current condition of system but also stay useful for all the time. Here is where the essence of dynamic location problems, considering time in modeling, appears [Owen and Daskin (1998); Farahani and Hekmatfar (2009) and Farahani et al. (2009)].

In general, decision maker selects the site which would be useful for a time horizon in time-dependent location problems but in location–relocation problems after selecting a primary location, relocation times improved facility’s location regarding conditions for a defined time horizon (Farahani et al. 2009).

Current et al. (1997) divided the models of dynamic location problems into two categories: explicitly dynamic and implicitly dynamic. In implicitly dynamic problems, all the facilities open at the same time and will be open during the time horizon. This category of problems seems to be static conceptually but as the problem parameters can change during the planning horizon, they are considered as dynamic location problems. In explicitly dynamic problems, unlike implicitly dynamic problems, facilities can be opened or closed several times for a defined time horizon.

The first survey of DLPs backs to the work of Owen and Daskin (1998) presenting the model of integer programming, dynamic programming, stochastic programming and scenario planning techniques. Farahani and Hekmatfar (2009) developed a framework and classified the models formulation and solution technique of DLPs. In addition, Arabani and Farahani (2012) surveyed the static and dynamic facility location problems and classified DLPs models to the several parts, then discussed about mathematical models, solution methods and applications of the available research in the literature since 2011.

There have been some motivation and contribution of our review paper based on the analysis of the previous research as follows:

  • According to the papers that have been reviewed, the most recent review paper in DLPs is the work of Arabani and Farahani (2012) discussed about 30 years from 1981 to 2011. Our paper presents modeling effort including those published after 2011, and review about 47 years of DLPs from 1968 until October 2015.

  • In the available review paper, all of the main elements of facility location dynamic problems are studied before 2011. Our paper presents a broader review of these research including those published after 2011, also we have been investigating the new elements in DLPs called the Dynamic Hub Facility Location Problems (DHFLPs).

  • We consider a wide range of characteristics for classification of the current and available DLPs research in the literature. Such characteristics as the number of objective, facilities and commodity, budget limits, capacity limits, number of relocation, type of parameters, facility and objectives and configuration have never been used in the past for classification the researches, so these detailed characteristics for categorizing the DLPs are comprehensively discussed in this review paper (Tables 1, 2).

    Table 1 Characteristics used for classification of the published models
    Full size table
    Table 2 Classification of DLPs modeling efforts based on the summary characteristics
    Full size table

  • Most of the review papers in DLPs emphasize on categorizing DLPs model without adequate attention on the application of solution method used. We discussed this gap in the current paper.

  • To the future research, the implementation of reliability, sustainability, different levels of services, planning for global logistics, relief management in crisis, queuing theory and risk of disruption needs to be taken into account as new recent trends and contributions in DLPs and these subjects are discussed more in conclusion section.

The emphasis of this review paper is on previously analyzed papers based on the available review research in the DLPs modelling efforts and gives us insight into some uncovered aspects in this field that have been published after 2009.

To search about the relevant paper in dynamic location problems, the only database such as sciencedirect and google scholar have been utilized. The keywords "Dynamic” AND "Facility” AND "Location” AND "Time Horizon” get us 107 research in this field. 45 different journals have been found based on these keywords about the above-mentioned researches. According to our investigation, most of these papers are published in "Computers & operations research”, "Computers & Industrial Engineering” and "European Journal of Operational Research”. We found the last published research in DLPs models before October 2015. All of mentioned aspects have been the scope and limitations of this review research.

This review paper is categorized as follows. In the next section, an assortment of DLPs based on their performance measure of the available literature such as number of facility, objective functions, commodity, parameters, configuration, relocation time, time horizon, applications and etc. will be provided. At the beginning of Sect. 3, a brief introduction of static facility location research is presented as a background for the review and then highlighted contributions in DLPs model formulation will be reviewed in 8 parts and the expansion trends of each part will be discussed. In Sect. 4, solution methods of DLPs is presented in two parts: (1) exact solution, and (2) heuristic, uncertain method and metaheuristic solution, regarding these two parts the solution techniques of accessible literature will be discussed. Section 5 addresses the application of DLPs models in terms of solution methods, industrial fields and real-world case studies. Finally, Sect. 6 suggests directions of future research and presents the conclusion of the whole review paper based on the current literature.

Classification of modeling efforts

Locating of facilities is one of the important aspects of strategic planning for widespread of private and public companies. Changes in population, market size and other environmental factors guarantee new planning challenges (new locating requirement and relocation) that is why, in an organization, planning is done in a way that facilities can be profitable for a period of time and be efficient during their life span. As a result, time changing is a necessary matter that must be considered (Owen and Daskin 1998).

Generally, one can study facility location problem based on essence of matter and used parameters are classified into two types: (1) certainty and uncertainty, (2) sustainability and unsustainability.

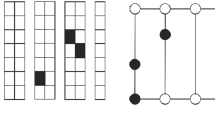
In general, dynamic location problems can be divided into several types based on different criteria such as cause of change, the number of relocations, the number of relocating facilities, relocation time and the time horizon. Classification of dynamic location problems based on these characteristics and the modeling discussed in this review paper are demonstrated in Fig. 1.

Fig. 1
figure 1

Classification of dynamic location problems (DLPs)

Full size image

First, the available classification in dynamic facility location problems adopted for the literature have been presented, then according to the structures proposed in the literature, as a result of reviewing the literature the integration and merging of these categories have been provided and discussed.

To provide different characteristics (criteria) for classifications of dynamic location problems, some of following definitions and different criteria will be presented:

Cause of change The most important classification is based on the cause of uncertainty that is classified two categories. (1) Changing because of future conditions, (2) Pattern of changes because of uncertainty due to limited knowledge of model input parameters (Rosenthal et al. 1978 and Owen and Daskin 1998).

One should consider that although in first category, changes exist but it is assumed that it is changing with deterministic and time-dependent parameters and has a distinctive pattern of change. But in the second category, it is possible that the pattern of changes is stochastic and it is not time dependent (Farahani et al. 2009).

Number and type of objective functions In dynamic location problems, number and type of models can be as follows: single objective or multi-objective, bi-level or multi-level, two-stage or multi-stage (Farahani et al. 2014).

Parameters According to the type of parameters used, models in dynamic location problems (DLPs) are categorized as deterministic, probabilistic, stochastic or fuzzy (Farahani et al. 2014).

Number of commodity and vehicle In a network, it is possible for commodity and vehicle to be more than one.

Facilities Exogenous and endogenous. In location problems, if the number of facilities that needs to be located is predetermined at each level, the model will be exogenous and if the optimal number is to be found by solving the model, it is an endogenous model (Farahani et al. 2014).

Levels and type of network The number of levels (types of services) can be variable in a system. In most of studied models, the network is only considered by one specific type of service, while in hierarchical location problems, different number of service levels are considered. However, dynamic location problems can be studied in different and multi-levels of services and the network type can be designed as hub network (Farahani et al. 2014).

Relocation time Discrete and continuous. In the first category, relocation is only possible in discrete points (pre-deterministic points) of time (Wesolowsky 1973); however, in the second category, almost any time of planning horizon and relocation is possible (Drezner and Wesolowsky 1991).

Time horizon Finite and infinite. Solving the dynamic location problems (DLPs) is due to uncertainty of future conditions. Postponing decision making as much as possible to collect information and improve forecasts is the best solution to manage uncertainty. This is why considering a time horizon is necessary in modeling. In addition, the main objective of dynamic location planning is not to determine location or relocation for the whole time horizon, but it is to find an optimum or near optimum for first period solution during the infinite horizon, hence whether the time horizon is finite or infinite, affects the decision of some aspects of the model (Daskin et al. 1992).

The number of relocation Single relocation and multiple relocation. In the single relocation, relocation is allowed in time horizon just once and in multiple relocations, new facilities are allowed to locate and change them more than once during the time horizon (Emamizadeh and Farahani 1997a, 1997b).

The number of relocating facilities Single facility and multiple facilities. In single facility, it is allowed to relocate only one facility during the time horizon whereas in the second category, it is allowed to relocate more than one facility during the planning horizon (Scott 1971 and Owen and Daskin 1998).

Constraints Limited and unlimited. Capacity of facility, rout, vehicle and reachable amount of budget in location problems can be limited or unlimited. Also capacities can expand or reduce in planning horizon (Farahani et al. 2014).

Application Application of model is investigated based on the real-world case studies. Some of the applications of dynamic location problems (DLPs) modeling consist of competitive systems, distribution systems, education, Emergency Medical Systems (EMS), hub systems, production–distribution systems, solid waste management systems and telecommunications networks (Farahani et al. 2014).

Appliqué particulars which are used to categorize published dynamic location problem (DLP) articles are shown in Table 1. Dynamic location problem (DLP) models are sorted based on their year of publication in ascending order since 1968 until now to clearly demonstrate the trend of this evolution (Table 2).

The cause of tree (CT) structure has been presented for the DLPs investigation, so that Table 1 is considered as a prerequisite for Table 2 and the characteristics used for classification in this table are complementary to Table 2. All entire assortments in Table 2 are sorted through prerequisite mentioned in Table 1.

The classifications in Table 2 are based on dynamic location problem (DLP) properties and provide some important insights:

  1. 1.

    According to probabilistic and stochastic nature and essence of dynamic location problems (DLPs), in most of the research on this matter, there has been emphasis on the use of deterministic parameters. Assuming a problem as a probabilistic or stochastic is the most important cause of problem complexity and its solution. So for simpler solution, the parameters are taken as they are deterministic ones.

  2. 2.

    Mostly to simplify the problem in the literature, number of commodity and levels of services are considered as single commodity and level, but in every system a variety of commodity and services (levels of network) can be found.

  3. 3.

    As it can be seen, mathematical model complexity is cause of using discrete times of relocations to simplify the objective function of problem in all of the studies; however, choosing the continuous time of relocations causes to show the rather real situation.

  4. 4.

    Until recently, assuming dynamic location problem (DLP) budget an unlimited parameter has been the norm; however, in the past recent years, choosing a specific budget has helped us to be closer to real world.

Basic dynamic location models

Facility location problems can be divided into two categories: static and dynamic problems (Farahani and Hekmatfar 2009).

Based on the previous dynamic facility location review papers such as Owen and Daskin (1998) and Arabani and Farahani (2012), at the start of this section, a brief introduction of static facility location research will be presented as a background for the review, better understanding of the change between the static and dynamic models, then highlighted contributions in DLPs model formulation will be reviewed in 8 parts and the expansion trend of each part will be discussed.

At the beginning, static model will be studied in this part and then, according to classification in part (2.1), it is now possible to present various mathematical models to formulate dynamic location problems (DLPs). The most common modeling, which has been applied by the literature, will be introduced in detail.

Static location models, first time was presented by Weber problem in 1909 to find a location of facility between the facilities to be located at \((x,\,y)\) among m points of demand (destinations) located at \((a_{i} ,\,b_{i} )\). The objective was to minimize the distance between the facility and costumers; transportation costs are assumed to be adequate to distance (Wesolowsky 1973).

\(d_{i} \,(x,\,y)\) is the distance between the facility to be located at \((x,\,y)\) and destination i located at \((a_{i} ,\,b_{i} )\); \(w_{i}\) a constant transforming distances into costs.

Location of facility is found by solving the following model (Wesolowsky 1973):

$${\text{Minimize}}\,\,\,\,\,\sum\limits_{i = 1}^{m} {\,\,w_{i} } \,.\,d_{i} \,(x,\,y)\,\,$$
(1)

Objective function (1) minimizing the distance between the facility and customers.

All of static location models can be argued in dynamic form as well. In dynamic location problem, there are two main criteria for decision making which make it easier to choose location. (1) Cost of new facilities or relocating the old ones in the time horizon. (2) Opening and closing time of facilities (Arabani and Farahani 2012).

There are also two important subsets in dynamic location problems: (1) in implicitly dynamic problems all facilities will be opened at the same time and will be active during the whole planning horizon. These problems seem to be static in the content but as parameters of problem could change in time horizon, they are considered dynamic problem. (2) Explicitly dynamic problems are the second part which, despite the implicitly dynamic problems, facilities can be opened or closed during the time horizon (Current et al. 1997).

Dynamic location problem has several mathematic models. Some of them which are explained in this literature consist of dynamic single facility location problems (DSFLPs), dynamic multiple facility location problems (DMFLPs), dynamic facilities location–allocation problems (DFLAPs), dynamic median facilities location problems (DMEFLPs), dynamic covering problems (DCPs), alternative dynamic approaches contains both stochastic & probabilistic dynamic facility location problems (SDFLPs & PDFLPs) and fuzzy dynamic facility location problems (FDFLPs), dynamic hub facility location problems (DHFLPs) and dynamic model with continuous time (DMCT).

Dynamic single facility location problems (DSFLPs)

Demands, costs and destination locations are forecasted with considering the time horizon of r discrete time periods, the static model (1) can be simplified and extended. Finding an optimal location of new facility in each period is the goal. The transportation costs of facility are independent of the distance of the facility they were transported (Wesolowsky 1973 and Farahani and Hekmatfar 2009).

\(m_{k}\) is the number of destinations in period k; \(f_{ki} (x_{k} ,\,y_{k} )\) the present value of the cost of shipping from the facility in period k to destination i; \(C_{k}\) the cost of moving at the beginning of period k; \(d_{k - 1\,\,,\,k}\) the distance the facility is moved at the beginning of period k.\(Z_{k}\)—if \((d_{k - 1\,\,,\,k} \ne 0)\), set \(Z_{k} = 1\), otherwise, set \(Z_{k} = 0\).

Location of facility is found by solving the following model (Wesolowsky 1973):

$${\text{Minimize}}\,\,\,\,\,\sum\limits_{k = 1}^{r} {\sum\limits_{i = 1}^{{m_{k} }} {f_{ki} (x_{k} ,\,y_{k} )} \,} \,\, + \,\,\sum\limits_{k = 2}^{r} {C_{k} } Z_{k}$$
(2)

Dynamic multiple facility location problems (DMFLPs)

Multi-period location allocation modeling is a problem that locates G new facilities among M candidate site to provide N demand points during the time horizon. This model proposed to find the optimal locations and relocations for response changing the demand over the planning horizon of k periods (Wesolowsky 1973 and Farahani and Hekmatfar 2009).

\(A_{jik}\) is the present value of the cost of assigning node i to node j in period k; \(C^{\prime}_{jk}\) the present value of the cost of removing a facility from site j in period k; \(C^{\prime\prime}_{jk}\) the present value of the cost of establishing a facility at site j in period k; \(m_{k}\) the maximum number of facility location changes allowed in period k.

\(x_{jik}\)—if node i is assigned to node j in period k, set \(x_{jik} = 1\), otherwise, set \(x_{jik} = 0\); \(y^{\prime}_{jk}\)—if a facility is removed from site j in period k, set \(y^{\prime}_{jk} = 1\), otherwise, set \(y^{\prime}_{jk} = 0\); \(y^{\prime\prime}_{jk}\)—if a facility is established at site j in period k, set \(y^{\prime\prime}_{jk} = 1\), otherwise, set \(y^{\prime\prime}_{jk} = 0\).

Objective function and constraints of the problem can thus be formulated as follows [Wesolowsky (1973) and Farahani and Hekmatfar (2009)]:

$${\text{Minimize}}\,\,\,\,\,\,\,\sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{M} {A_{jik} x_{jik} + \sum\limits_{k = 2}^{K} {\sum\limits_{j = 1}^{M} {(C^{\prime}_{jk} y^{\prime}_{jk} + C^{\prime\prime}_{jk} y^{\prime\prime}_{jk} )} } } } }$$
(3)

Subject to:

$$\sum\limits_{j = 1}^{M} {x_{jik} } \, = 1\quad \forall i,k$$
(4)
$$\sum\limits_{i = 1}^{N} {x_{jik} } \, \le Nx_{jjk} \quad \forall j,k$$
(5)
$$\sum\limits_{j = 1}^{M} {x_{jik} } = G\quad \forall k$$
(6)
$$\sum\limits_{j = 1}^{M} {y^{\prime}_{jk} } \le m_{k}\quad \forall k \ge 2$$
(7)
$$x_{jjk} - x_{jj,k - 1} + y^{\prime}_{jk} - y^{\prime\prime}_{jk} = 0\quad \forall j,\,\,\,k \ge 2$$
(8)
$$\begin{aligned} x_{jik} \ge 0\quad \forall i \ne j; \hfill \\ y^{\prime}_{jk} ,y^{\prime\prime}_{jk} \ge 0\,\,\,\,\,\,\,\forall j,k; \hfill \\ x_{jjk} = \{ 0,1\} \quad \forall j,k \hfill \\ \end{aligned}$$
(9)

Constraint (4) demonstrated single allocation. Constraint (5) guarantees that point i is assigned to facility j, when the facility is established in node j. Constraint (6) and (7) ensure that in each period, G facility can be established and the maximum number of changes allowed for facilities should be less than the \(m_{k}\). As G number of facilities can be built in each period, Constraint (8) represents an equilibrium limit to establish the mentioned assumption. Constraint (9) is decision variables of problem.

Dynamic facilities location allocation problems (DFLAPs)

Location allocation problems are not only to find the best place for facilities but also to allocate facilities to customers to satisfy their demands optimally (Arabani and Farahani (2012). Discrete DFLPS was first studied by Scott (1971), and then Wesolowsky (1973) and Wesolowsky and Truscott (1975) expanded dynamic single facility location problems and dynamic multiple facility location problems.

Daskin et al. (1992) studied future effects of uncertainty in DFLAPS conditions and the main aim was not to consider the location and relocation in time horizon but to find an optimum or near-optimum solution for the first period. The research of Chardaire et al. (1996) was on demand changes in multi-period in DFLAPs. Saldanha da Gama and Captivo (1998) worked on improving heuristic solution approach. Antunes and Peeters (2000) studied education network planning model with changing general facilities capacity and then in the next year a new solution was established. Averbakh et al. (2007) worked on expanding the dynamic programming algorithm.

Planning and designing logistic distribution system in different dynamic levels by Manzini and Gebennini (2008), an integrated production–distribution model for the dynamic location and allocation problem with safety stock optimization by Gebennini et al. (2009) and DFLAPs in health department of veterans by Benneyan et al. (2012) were presented.

Dynamic median facilities location problems (DMEFLPs)

Extension of p-median model, from 1-median problem was the most important part of median; it was made to find the best location for p facilities to minimize the sum distance for every point of demand to closest facility (Arabani and Farahani 2012).

Dynamic location problem applying a scenario planning is presented in this section. Regarding the description of the model, the objective function minimizes expected regret. All of the scenarios and candidate location for new facilities are predetermined and common. The probability of each scenario should be estimated based on information and having different scenarios make the demand assignments in each scenario be different to the other one (Owen and Daskin 1998).

\(k\) is the index of possible scenarios; \(P\) the number of new facility; \(h_{ik}\) demand at node i under scenario k; \(d_{ijk}\) distance from node i to facility site j under scenario k; \(\hat{\nu }_{k}\) optimal P-median solution value for scenario k; \(q_{k}\) scenario probability for scenario k; \(R_{k}\) the regret associated with scenario k, \((R_{k} = \nu_{k} - \hat{\nu }_{k} )\).

\(y_{ijk}\)—if demand node i is assigned to facility j under scenario k, set \(y_{ijk} = 1\), otherwise, set \(y_{ijk} = 0\); \(x_{\,j}\)—if facility site j locates at potential, set \(x_{\,j} = 1\), otherwise, set \(x_{\,j} = 0\).\(\nu_{k}\), under the conditions of compromise locations:

$$\nu_{k} = \sum\limits_{i} {\sum\limits_{j} {h_{ik} d_{ijk} y_{ijk} } }$$

Objective function and constraints of the problem will be as below (Owen and Daskin 1998):

$${\text{Minimize}}\,\,\,\,\,\,\,\sum\limits_{k} {q_{k} R_{k} }$$
(10)

subject to:

$$\sum\limits_{j} {x_{j} = P}$$
(11)
$$\sum\limits_{j} {y_{ijk} = 1} \,\,\,\,\,\,\,\,\,\forall i,k$$
(12)
$$y_{ijk} - x_{j} \le 0\,\,\,\,\,\,\,\,\,\forall i,j,k$$
(13)
$$R_{k} - \sum\limits_{i} {\sum\limits_{j} {(h_{ik} d_{ijk} y_{ijk} } } - \hat{\nu }_{k} ) = 0\,\,\,\,\,\,\,\,\,\forall k$$
(14)
$$y_{ijk} = \{ 0,1\} \,\,\,\,\,\,\,\forall i,j,k$$
(15)
$$x_{j} = \{ 0,1\} \,\,\,\,\,\,\,\forall j$$
(16)

Constraint (11) represents the maximum number of new facilities to be located. Constraint (12) point i, under scenario k will be definitely supplied by facility j. Constraint (13) guarantees that in scenario k, demand i can be assigned to facility j when facility was opened. Constraint (14) demonstrates the regret of scenario k. Constraint (15) and (16) are decision variables.

Wesolowsky (1973) was the first one who studied DMEFLPs. Erlenkotter (1981) tried to develop the algorithms for DMEFLPs. Drezner and Wesolowsky (1991) studied multi-relocation in time horizon while maximum expected cost lows down to minimum. Shulman (1991) presented a schedule to setup facilities in location, to minimize costs during the time horizon. Galvao and Santibanez-Gonzalez (1992) studied a heuristic approach to solve dynamic p-median problem. Current et al. (1997) developed DMEFLPs for conditions which number of facilities is unknown; also changing the size of facilities and dependency of setup cost to number of customers were studied by Averbakh et al. (1998).

Dias et al. (2006) have established DMEFLPs in three different scenarios. Averbakh et al. (2007), Dias et al. (2008a), Dias et al. (2008b), Albareda-Sambola et al. (2009) worked on developing the model and presenting a new solution. Farahani et al. (2009) studied single facility with multi-relocation in which weight of demand point is dependent on time.

Dynamic covering problems (DCPs)

In general, every customer can ask for services from any facility; customer and facility have a specific distance to each other, which is called coverage distance, thus every facility can service depending on the coverage requirement (Arabani and Farahani 2012). It was for the first time ever, in 1980, an alternated approach was presented to solve the problem of locating. It is a combined model including multi-aim TDCPs for every time limit. This approach was considered an alternate approach to solving facility location problems, inspired by the public sector need to locate emergency medical service (EMS) systems.

\(d_{ijt}\) is the shortest distance or time from node i to node j in period t; \(N_{it}\) set of sites which can cover node i in period t; \(h_{it}\) demand weight on node i in period t;\(P_{t}\) number of facilities operational in period t.\(x_{jt}\)—if a facility is operating at site j in period t, set \(x_{jt} = 1\), otherwise, set \(x_{jt} = 0\); \(Y_{it}\)—if a facility is operating at node i in period t, set \(Y_{it} = 1\), otherwise, set \(Y_{it} = 0\).

The mathematical model formulation is given by the following (Schiling 1980):

$${\text{Maximize }}\sum\limits_{i} {h_{it} Y_{it} } \quad\forall t = 1,2, \ldots ,T$$
(17)

Subject to:

$$\sum\limits_{{j \in N_{it} }} {X_{jt} } \quad \ge Y_{it} \;\forall i,t$$
(18)
$$\sum\limits_{j} {X_{jt} } \, = P_{t} \quad\forall t = 1,2, \ldots ,T$$
(19)
$$X_{jt} \ge X_{j,t - 1} \quad\forall j,t = 2, \ldots ,T$$
(20)
$$X_{jt} \in \{ 0,1\} \quad \forall j,t = 1,2, \ldots ,T$$
(21)
$$Y_{it} \in \{ 0,1\} \quad \forall i,t = 1,2, \ldots ,T$$
(22)

This proposed model combines T maximal covering problems; \(Y_{it}\) is equal to unity only when facilities are established at sites in the set \(N_{it}\) (Constraint 18). The number of operational facilities in period \(t\) is \(P_{t}\) (Constraint 19). Constraint (20) shows that when the center is opened it will be opened continuously to next periods too. Constraints (21) and (22) are decision variables.

To be specific first, DCPs were presented by Schiling (1980) and Gunawardane (1982) developed it in the way that penalties for opening or closing the facilities would reduce the amount of changes of relocation. Gendreau et al. (2001) studied the ambulances problem, and the goal was to maximize total demand covered and minimize travel cost. The model was also improved by Brotcorne et al. (2003) to probabilistic model which means ambulances operate as servers in a queueing system and cannot always answer a call. Rajagopalan et al. (2008) made a new covering model in dynamic problems to minimize the number of ambulances and their locations for the case which all of them are busy. Fazel Zarandi et al. (2013) developed a new method for DCPs.

Alternative dynamic approaches

Stochastic and probabilistic dynamic facility location problems (SDFLPs & PDFLPs)

As it was mentioned in part 2, uncertainty occurs as input parameters for two reasons: (1) future conditions and (2) lack of knowledge (Owen and Daskin 1998 and Farahani and Hekmatfar 2009). As a whole, there are two approaches for optimization under an uncertain environment: stochastic programming (SP) and robust optimization (RO). In stochastic programming (SP) it is assumed that value of uncertain parameters are following the probability distributions with known parameters; however, in robust optimization it is assumed that no information about probability distributions is reachable except few data for the specification of intervals containing the uncertain values (Ghaffari-Nasab et al. 2015). Like most of stochastic models, it is possible to point out stochastic problems in scenario planning approach template (Arabani and Farahani 2012). In this model, m demand node, n candidate, location and k possible scenario exist (the parameter is considered under the scenario k) (Arabani and Farahani 2012).

Definition of parameters \(h_{ik}\), \(d_{ijk}\), \(\hat{v}_{k}\), \(q_{k}\), \(R_{k}\) and decision variables \(x_{j}\) and \(y_{ijk}\) are like mentioned models in part 3.4.

\(m_{k}\) is the large constant \(m_{k} \ge R_{k}\); \(F\) available facilities. \(z_{k}\)—if the maximum regret is minimized under a set including scenario k, set \(z_{k} = 1\), otherwise, set \(z_{k} = 0\).

Now the stochastic programming model can be formulated as follows (Arabani and Farahani 2012):

$${\text{Minimize}}\,\,\,\,\,\,\,Z$$
(23)

Subject to:

$$\sum\limits_{j = 1}^{n} {x_{j} } = F$$
(24)
$$\sum\limits_{j = 1}^{n} {y_{ijk} = 1}\quad \forall i,k$$
(25)
$$y_{ijk} - x_{j} \le 0\quad \forall i,j,k$$
(26)
$$R_{k} - \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{m} {(h_{ik} d_{ijk} y_{ijk} } } - \hat{\nu }_{k} ) = 0\quad \forall k$$
(27)
$$\sum\limits_{k = 1}^{K} {q_{k} R_{k} } \ge \alpha$$
(28)
$$Z - R_{k} + m_{k} (1 - z_{k} ) \ge 0\quad \forall k$$
(29)
$$x_{j} = \{ 0,1\} ,\,\,\,\,y_{ijk} = \{ 0,1\} ,\quad z_{k} = \{ 0,1\} \quad \forall i,j,k$$
(30)

Objective function (23) minimizes the \(\alpha\)-reliable minimax regret. Constraint (24) represents the available number of facilities to be located. Constraint (25), demonstrated single allocation. If a facility is not located at node j, the demand of node i cannot be satisfied under scenario k (Constraint 26). Constraint (27) defined the regret attributed to scenario k. The least possible probability of selecting scenario must be \(\alpha\) (Constraint 28). Constraint (29) identified the maximum regrets. Constraint (30) is decision variable.

So, as an alternate to SDFLPs, location and relocation of facility is under a decision maker’s control. The model is relocation policy that minimizes the expected present worth of all costs (Rosenthal et al. 1978).

$${\text{Minimize}}\,\,Z = E\left[ {\sum\limits_{t - 1}^{a} {\{ F(X_{t - 1} ,X_{t} ) + G(X_{t} ,A_{t} )\} B^{t - 1} } } \right]$$
(31)

\(X{}_{t}\) is server location at time t, decision variable; \(A_{t}\) customer location at time t, stochastic; \(N\) known set of possible location for both \(N:\{ 1, \ldots ,n\}\); \(F\) known server relocation cost matrix, \(n \times n\); \(G\) known service cost matrix, \(n \times n\); \(P\) known Markov transition matrix for customer location, and \(n \times n\); B known discount factor (Rosenthal et al. 1978).

A discrete time process evolves as follows: (1) observes \((X_{t} ,A_{t - 1} )\) and chooses \(X_{t}\), (2) relocating cost \(f(X_{t} ,A_{t - 1} )\) is incurred, (3) chance probabilistic \(A_{t}\) is realized and (4) service cost \(g(X_{t} ,A_{t} )\) is incurred (Rosenthal et al. 1978).

Probabilistic or stochastic demand parameter was first, presented by Henig and Gerchak (1986) and then Sherali (1991), Lee and Jeong (2009) and Zeballos et al. (2014) improved it in PDFLPs. Aghezzaf (2005), Romauch and Hartl (2005), Gabor and Van Ommeren (2006), Manzini and Gebennini (2008), Acar et al. (2009) and Wang (2014) studied the effect of demand parameter uncertainty in SDFLPs. Also Marufuzzaman and Eksioglu (2014) and Barkaoui and Boukhtouta (2015) developed probability of disruption and visit customer.

Fuzzy dynamic facility location problems (FDFLPs)

First, application of fuzzy approach in dynamic location problems (DLPs) will be classified into two categories: (1) selecting facilities location: to do this, there are three strategies being used: analytic hierarchy process (AHP), fuzzy TOPSIS, fuzzy information axiom; (2) location allocation problems: when using the fuzzy logic, in location allocation problems, Wen’s model can be useful. Fuzzy parameters in the literature are demands, facility capacity and delivery cost (Arabani and Farahani 2012).

An electronic commerce (e-commerce) system has several subsets such as supplier \(i \in I\), distribution centers \(j \in J\) and customers  \(k \in K\) with multi-commodity \(l \in L\)(Lau et al. 2010).

\(H_{il}\) is the unit supply cost of node i for the lth kind of commodities; \(C_{ijl}\) unit transport cost from node i to node j for the lth kind of commodities; \(U_{jl}\) unit inventory cost of node j for the lth kind of commodities in the distribution period; \(S_{jl}\) unit handling cost of node j for the lth kind of commodities; \(F_{j} (v)\) setup cost at node j (Eq. 32); \(F_{j0}\) setup cost when v is less than critical capacity; \(\tilde{B}_{jk}\) fuzzy delivery cost per unit from node j to customer k (Eq. 33); \(B_{j} (I_{T} )\) cost of a tour through a customer \(i \in I_{T}\) starting from node j; \(v\) capacity of node j; \(N_{j}\) and \(M_{j}\) critical capacity and maximal capacity; \(\tilde{A}_{il}\) fuzzy supply capacity of supplier i for the lth kind of commodities in the plan period; \(\tilde{D}_{kl}\) fuzzy demand of customer k for the lth kind of commodities in the plan period; \(m\) number of transport periods in the plan period; \(n\) number of distribution periods in the transport period; \(x_{ijl}\) number of the lth kind of commodities transported from supplier i to distribution center j in each transport period; \(P\) maximum number of selected distribution centers; \(Q(I_{T} )\) total commodity weight units of the cluster; \(d_{jk}\) distance between distribution center j and customer k; \(S_{\hbox{max} }\) maximum tour length of vehicles; \(E_{j0}\) coefficient of setup cost; \(\phi\) coefficient of economies of scale, \(\phi \in (0,1)\); \(r\) scale coefficient of handling cost; \(w_{l}\) unit bulk coefficient of the lth kind of commodities; \(q_{l}\) unit weight coefficient of the lth kind of commodities \(l \in L\) (Lau et al. 2010).

$$F_{j} (v) = \left\{ \begin{aligned} &F_{j0} + E_{j0} (v - N_{j} )^{\phi } \quad N_{j} < v \le M_{j} \hfill \\ &F_{j0} ,\quad 0 < v \le N_{j} \hfill \\ &0,\quad v = 0 \hfill \\ \end{aligned} \right.$$
(32)
$$B_{jk} = \left\{ \begin{aligned} \infty ,&\quad if\,\,2d_{jk} > S_{\hbox{max} } \hfill \\ \frac{{B_{j} (I_{T} )}}{{Q(I_{T} )}},&\quad {\rm otherwise} \hfill \\ \end{aligned} \right.$$
(33)

\(y_{j}\)—if distribution center j is selected, set \(y_{j} = 1\), otherwise, set \(y_{j} = 0\); \(z_{jk}\)—if customer k is delivered by distribution center j, set \(z_{jk} = 1\), otherwise, set \(z_{jk} = 0\).

Now the fuzzy programming model for location of distribution center can be formulated as follows (Lau et al. 2010):

$$\begin{aligned} {\text{Minimize}}\,\,\,\,\,\,\,m\sum\limits_{i \in I} {\sum\limits_{l \in L} {H_{il} \sum\limits_{j \in J} {x_{ijl} } } } + m\sum\limits_{i \in I} {\sum\limits_{l \in L} {\sum\limits_{j \in J} {C_{ijl} x_{ijl} } } } \hfill \\ \quad + \sum\limits_{j \in J} {F_{j} (v)} \sum\limits_{i \in I} {\sum\limits_{l \in L} {w_{l} x_{ijl} } } + m\sum\limits_{i \in I} {\sum\limits_{l \in L} {\sum\limits_{j \in J} {\sum\limits_{\tau = 1}^{n} {U_{jl} } } } } \frac{{x_{ijl} }}{n}\tau \hfill \\ \quad + m\sum\limits_{i \in I} {\sum\limits_{l \in L} {\sum\limits_{j \in J} {S_{jl} x_{ijl} } + \sum\limits_{j \in J} {\sum\limits_{k \in K} {\tilde{B}_{jk} z_{jk} } } } } \sum\limits_{l \in L} {q_{l} \tilde{D}_{kl} } \hfill \\ \end{aligned}$$

subject to:

$$m\sum\limits_{j \in J} {x_{ijl} } \le \tilde{A}_{il} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall i \in I,\,\,l \in L$$
(35)
$$m\sum\limits_{i \in I} {x_{ijl} } = \sum\limits_{k \in K} {\tilde{D}_{kl} z_{jk} \,\,\,} \,\,\,\,\,\forall j \in J,\,\,l \in L$$
(36)
$$\sum\limits_{i \in I} {\sum\limits_{l \in L} {w_{l} x_{ijl} } } \le M_{j} y_{j} \,\,\,\,\,\,\,\,\,\,\forall j \in J$$
(37)
$$\sum\limits_{j \in J} {y_{j} } \le P\,$$
(38)
$$\sum\limits_{j \in J} {z_{jk} } = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall k \in K$$
(39)
$$ry_{j - } \sum\limits_{k \in K} {z_{jk} } \ge 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall j \in J$$
(40)
$$\begin{aligned} x_{ijl} \ge 0 \quad \hfill \\ y_{j} \in \{ 0,1\} \hfill \\ z_{jk} \in \{ 0,1\} \quad \forall i \in I,\quad \forall j \in J,\quad \forall l \in L \hfill \\ \end{aligned}$$
(41)

Fuzzy constraints (35) and (36) assure that all commodities transported from suppliers are not more than its capacity and there should be balance between every input and output center. Constraints (37), (38) and (39) show the maximum capacity and number of every distribution center and single allocation. Every selected distribution center services several customers (40). Constraint (41) is decision variable.

Lau et al. (2010) was the first one who presented FDFLPs with fuzzy parameters of demand, facility capacity and delivery cost in an e-commerce network and then two fuzzy parameters, demand and facility capacity were developed by Taghipourian et al. (2012) in dynamic Hub facility location problems. Fuzzy demand was studied in two articles: dairy facility location problem by Jouzdani et al. (2013) and location-routing problem by Nadizadeh and Hosseini Nasab (2015).

Dynamic hub facility location problems (DHFLPs)

In 2010, dynamic hub facility location problems were first studied to minimize fixed cost, transportation and routing costs. Set of potential hub location \(i,j \in H\), set of subsets of H including one or two hubs  \(e \in E\), set of commodity in time horizon \(t \in T\), all are reachable.

\(W_{k}^{t}\) is the amount of commodity k to be transported at period t; \(f_{i}^{t}\) fixed cost of opening a hub at node i at the beginning of period t; \(g_{i}^{t}\) cost of operating a hub at node i in period t; \(q_{i}^{t}\) recovery gain associated with closing a hub located at node i in period t; \(\hat{F}_{ijk}^{t}\) transportation cost or routing commodity k, \(\hat{F}_{ijk}^{t} = W_{k}^{t} (\,\,d_{o(k)i}^{t} \,\, + \,\,\alpha d_{ij}^{t} \,\, + \,\,d_{jd(k)}^{t} \,\,);\) \(F_{ek}^{t}\) undirected transportation cost \(F_{ek}^{t} \in \hbox{min} \,\,\{ \,\,\hat{F}_{ijk}^{t} \,\,\,,\,\,\,\hat{F}_{jik}^{t} \,\,\};\) \(\alpha\) discount factor between two hub nodes; \(o(k),d(k)\) origin and destination nodes of commodity k.

\(x_{ek}^{t}\)—if commodity k at period t uses hub edge e, set \(x_{ek}^{t} = 1\), otherwise, set \(x_{ek}^{t} = 0\); \(z_{i}^{t}\)—if a hub facility is located at node i in period t, set \(z_{i}^{t} = 1\), otherwise, set \(z_{i}^{t} = 0\).

The mathematical model formulation is given by the following (Contreras et al. 2010):

$$\begin{aligned} {\text{Minimize}}\,\,\,\,\,\,\,\,\,\,\,\,\sum\limits_{i \in H} {\sum\limits_{t \in T} {f_{i}^{t} (1 - z_{i}^{t - 1} )z_{i}^{t} } } + \sum\limits_{i \in H} {\sum\limits_{t \in T} {g_{i}^{t} (1 - z)z_{i}^{t} } } \hfill \\ \quad - \sum\limits_{i \in H} {\sum\limits_{t \in T} {q_{i}^{t} (1 - z_{i}^{t} )z_{i}^{t - 1} } } + \sum\limits_{e \in E} {\sum\limits_{k \in K} {\sum\limits_{t \in T} {F_{ek}^{t} } } } x_{ek}^{t} \hfill \\ \end{aligned}$$

subject to:

$$\sum\limits_{e \in E} {x_{ek}^{t} } = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall k \in K,\,\,t \in T$$
(43)
$$\sum\limits_{{\{ e \in E:\,\,\,i \in e\} }} {x_{ek}^{t} } \le z_{i}^{t} \,\,\,\,\,\,\,\,\forall i \in H,\,\,k \in K,\,\,t \in T$$
(44)
$$x_{ek}^{t} \ge 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall e \in E,\,\,k \in K,\,\,t \in T$$
(45)
$$z_{i}^{t} \in \{ 0,1\} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall i \in H,\,\,t \in T$$
(46)

Constraint (43) assures each commodity from origin–destination path has single allocation in period \(t\). Constraint (44) also emphasizes that commodities route has to pass hub nodes. Constraints (45) and (46) show decision variables.

Specifically, first DHFLPs were presented by Contreras et al. (2010) and then, Terymourian et al. (2011) studied dynamic virtual hub location problem in airline networks with adverse weather conditions. Also it was developed by Taghipourian et al. (2012) with fuzzy parameters. Correia et al. (2012) investigated existence of exogenous budget available at the beginning of time period for installing and removing hubs. Marufuzzaman and Eksioglu (2014) developed an economic model, which is based on an efficient hub network, to hedge against fossil fuels fluctuations and natural disasters. Dynamic hub facility location model that has logistic servers was presented by Horhammer (2014). Horhammer (2014) minimized total costs of collection, distribution, operational, fixed, closing and changing facilities capacity. Bashiri and Hamidian (2015) developed p-median hub location problem with multiple allocations and Gelareh et al. (2015) expanded dynamic location allocation hub network with limited budget.

Dynamic model with continuous time (DMCT)

Dynamic model with continuous time are most appropriate for strategic planning to find the best location and relocation time to serve and expanding demand with minimizing the transportation and relocation costs. S is a service region (Campbell 1990).

\(K(t)\) is the number of terminals in the system at time t; \(X_{j} (t)\) location of terminal j at time t; \(M(t)\) the cumulative number of terminal relocations at time t; \(\rho (x\,,\,\,t)\) demand density at location x at time t; \(q\) discount rate (proportion of value per unit time); \(r\) the total discounted relocation cost; \(D(x\,,\,\,X(t))\) average transportation cost per shipment at time t originating at location x.

Objective function and constraints of the problem should be as it is mentioned below (Campbell 1990):

$$\begin{aligned} {\text{Minimize }}C(X(t)) = & \int\limits_{{t_{0} }}^{\infty } {K(t)\;} e^{ - qt} \,dt + \int_{{t_{0} }}^{\infty } {M(t)\,} r\,e^{ - qt} \,{\text{d}}t \\ \quad + \int\limits_{{t_{0} }}^{\infty } {\left[ {\int\limits_{s} {\rho (x\,,\,\,t)\,D(x,X(t))dx} } \right]} \,e^{ - qt} \,{\text{d}}t \\ \end{aligned}$$
(47)

Solution approaches and algorithms for dynamic location problems

A large variety of algorithm methods are proposed to solve dynamic location problems (DLPs). Solution methods can be divided into two general categories: (1) exact methods, (2) heuristic and metaheuristic. Exact algorithm of linear programming such as branch-and-bound solution technique is a method in which at every node of the branching tree are obtained lower and upper bounds (Land and Doig 1960), Lagrangian relaxation (LR) method which is used for solving large-scale combinatorial optimization problems (Fisher 1981), Benders decomposition algorithm allows to solve a linear programming problem with complicating variables using Benders cut (Benders 1962), dynamic programming (DP) breaking the complex problems down into a collection of simpler sub-problems (Bellman 1975), etc. These exact methods more common and usually used to solve the small and medium size, but these solution methods are not profitable to solve the larger size and complex dimensional problems. Nowadays, for solving the complex dynamic location problem, which are called NP-hard problems, heuristic and metaheuristic approaches such as genetic algorithm (GA) (Holland 1992), tabu search (TS) (Glover 1986) and simulated annealing (SA) (Kirkpatrick et al. 1983) or combination of them are developed. These methods give the near-optimum solution and are applied for the time that obtaining the optimum solution is not possible.

Application of exact solution method in dynamic location problems

Classical exact algorithms such as integer programming (IP) and dynamic programming (DP) used since the mid-1960s to solve dynamic location problems when the size is traceable (e.g., small and medium size). In Table 3, all the related researches since 1986 till now are studied individually and summarized based on the exact solution methods which have been used to solve the dynamic location models.

Table 3 Exact solution algorithm in DLPs
Full size table

Application of heuristic, uncertain method and meta-heuristic solution method in dynamic location problems

The first heuristic approach for dynamic location problems was developed at the end of 1960s. As the solutions being used for small and medium size were not efficient for larger size heuristic, meta-heuristic approaches such as genetic algorithm (GA), tabu search (TS), and simulated annealing (SA) or combination approaches were used. All the published researches since 1986 to now have been studied and classified in Table 4 based on their heuristic and metaheuristic and uncertain methods.

Table 4 Heuristic, uncertain method and meta-heuristic solution algorithm in DLPs
Full size table

More than 56 % of published articles listed in Tables 3 and 4 have utilized exact solution methods and less than 44 % heuristic and metaheuristic methods to solve dynamic location problems. For instance, about 21 % of articles have utilized branch-and-bound methods, about 24 % dynamic programming (DP) methods, about 12 % Lagrangian relaxation (LR) and about 9 % Bender’s decomposition methods.

In recent years, solution methods such as fuzzy programming, branch-and-cut, branch-and-price, branch-and-fix, fuzzy chance constraint programming, robust optimization or a combination of exact method and heuristic or metaheuristic have been used.

Applications of solution method, application fields and real-life case studies

In this section, we study the literature of dynamic location problems (DLPs) pursuant to application basis as well as the relevant case studies. Table 5 categorizes the literature of DLPs in terms of its applications due to the solution methods, industrial context and fields. In addition, the applications and description of real-world case studies are classified in Table 6. According to Tables 5 and 6, the production–distribution systems are studied more than some other categories. From Tables 5 and 6 it can also be recognized that two subjects of competition problems and hub location problems are more attended in the recent years. 75 % of dynamic location problems on real-world case studies were published after 2000 (in the last 15 years).

Table 5 Applications of solution method and application fields for DLPs
Full size table
Table 6 Real-life case for DLPs
Full size table

Conclusions and future trends

In this review paper, it has been attempted to prepare a trend of dynamic location problems literature and other relevant concepts, all the published papers are studied and classified according to their properties of problem and parameters. Objective functions, optimization models, parameters, constraints, techniques and solution method based on two categories: (1) exact algorithm; (2) heuristic and metaheuristic algorithms have been analyzed and categorized for all the published papers.

Moreover, there is a classification of dynamic location articles based on application and case studies (industrial field), that are gathered and classified in this review paper. Some of possible trend for future works, based on gapes of recent literature are presented to conduct future studies on dynamic location problems.

Our analysis on the characteristics of models, solution methods and applicability of published papers suggests the ways for future research in Dynamic location problems (DLPs).

To the future research, the implementation of variety of services (hierarchical network), reliability, sustainability, planning for global logistics and relief management in crisis, waiting time for services (queuing theory) and risk of facility disruption need to be taken into account as new recent trends and contributions and further study in DLPs. Specific conclusion emerging from the present study have been discussed comprehensively as follows:

  • Dynamic facility location models are vastly used in general facility location problems. In most recent papers, single services for customers have been considered, while, variety of services expand the model to introduce the hierarchical problem with different levels, flow pattern and configuration of network. In this time, we can understand the importance of hierarchical location problem, which is studied by Melachrinoudis et al. (1995), Hinojosa et al. (2000), Melachrinoudis and Min (2000), Syam (2002), Dias et al. (2007b), Dias et al. (2008a), Manzini and Gebennini (2008), Thanh et al. (2008) and Gebennini et al. (2009); needs to be focused more.

  • To manage demanding customers more efficiently and also satisfy demands faster, systems should be designed such as capable of managing several facilities (several systems) instead of one facility (one system). Actually some papers are written about this subject, but having several facilities in dynamic location problem (DLP) needs to be attended.

  • Considering multi-facilities (multi-systems) to satisfy demands, brings facility (systems) competitions that only Miller (2007) and Bozkaya (2010) have attended. Having competitive facility, pricing and coalition of systems in dynamic location problem (DLP) can be another field to study.

  • Combination of continuous models in dynamic location problem (DLP) is one of the fields that is attended less. Almost in all the published papers, time and location of relocation is considered as discrete points. Hence, attending to continuous models and combining that with dynamic location problem (DLP) can have more realistic results than discrete models.

  • In recent years the events happened suddenly and in numbers, so in DLPs, the crisis management needs to be considered in case studies. In real-world logistic problems, system operates in two different moods: normal and abnormal (crisis).

  • Normal mood of system is when there are no threats or changes. Planning for logistic relief management in crisis which includes two parts: natural crisis and by-human crisis (such as earthquake, flood, storm and war) means considering uncertainties, to confront sudden happenings; this problem is one of the matters that should be studied more in dynamic location problem (DLP) systems.

  • Also sustainability of modeling and paying attention to particular points like social, cultural and political factors, environmental effects, green supply chain and attending to logistic systems pollution have economic aspects, can be one of the most important challenges in dynamic location problem (DLP).

  • In all the distribution systems, waiting time, which means the time that customers can wait until they get the services they want has significant impression on their decision, and in location problem it is called queue (queuing theory). Designing a system optimally without having a sight on density and bottleneck made by customers waiting for services, is not possible. Dynamic location problem (DLP) approaches need to get merged with methods like queuing theory that can be more synchronized or adapted with real conditions of every system, namely existence of queue.

  • When a group of facilities gets set up, in every period of time, it is possible that one or some of them, suddenly disrupt or destroy and this can have several reasons such as depreciation as a result of long-term usage, environmental or political elements and so on, and it is unavoidable. Hence, considering the possibility of disruption and the risk of destruction increases the reliability of developed models. Nadizadeh and Hosseini Nasab (2014) have studied it in dynamic location problem (DLP). This matter can be studied as a research subject that is attended little yet.

  • In most of the existing models of the literature, parameters of models are taken as deterministic ones; however, in real world they are uncertain. It is not possible to forget the probabilistic and stochastic essence of dynamic location problem (DLP). Having uncertain input parameters cause to use Probabilistic Programming (PP), Stochastic Programming (SP), Fuzzy Approach and Robust Optimization (RO) or other optimizing methods and also combining them we can confront uncertainty. Considering the uncertainty is one of the primaries in this field.

  • Attention to the limitation of sources and capacities in location problems is essential. Sources and capacities of facilities have been considered changeless during the horizon planning till now so with regards to dynamic system argument it is clear that reachable sources and capacities of facilities are changing during the time and can have increases or decreases hence it is possible to have a backup system to confront the lack of enough sources and capacities. Thus, considering to existing constraints in real world improves the DLP modeling.

  • Application of new objective functions instead of considering the allocation based on the closest facility or minimizing the costs and distances, or maximum benefit is the factor that should be considered, regarding time conditions during the time horizon. Multi-objective functions with several criteria in bi-level, multi-level, bi-stage and multi-stage, with more complex objectives, can conduct us to a more real condition.

  • Solution approaches are divided into two parts: exact solution, heuristic and metaheuristic solution. In DLPs, exact algorithm is not developed with time passing. Regarding the complexity of DLPs, algorithms developing is hard. For this reason, heuristic and metaheuristic algorithms or a combination of them are more attended in this subject. However, these methods, will not give us an accurate solution; hence, using some techniques to have a better analysis of these approaches, combining them and developing existing methods can produce a better condition in DLP solutions.