Introduction

Supply chain management (SCM) has received great attention in both industry and academia recently. SCM consists of procurement of raw materials and components, turning them into finished products, and distribution of products to customers aiming at minimization of the total cost and while satisfying the customer demands as much as possible (Singh 2014). In SCM studies, based on the time horizon, three planning levels are recognized for such researches: strategic level decisions, tactical level decisions and operational level decisions. Strategic level decisions belong to the long-term horizon and they are the most important decisions because they influence performances of all of the supply chain echelons significantly. One of these strategic decisions is supply chain network design (SCND) that it is the most vital and critical decision in supply chain. Its purpose is location of supply chain facilities and allocation of elements to each other with minimum total cost (Pishvaee and Razmi 2012; Govindan et al. 2015). Tactical level decisions are made for the medium term horizon usually once a year or once in each season. These decisions include transportation mode selection, inventory policies, production decisions, supplier selection and so on. The operational decisions are relevant to the short-term horizon and they are made once a weak or day to day such as routing and scheduling and so on.

Most papers in the supply chain area speak about strategic decisions and determine the location of facilities and the quantity of shipments between them. Considering of other tactical decisions (except the flow) with strategic level decision is studied rarely. For example, (Goetschalckx et al. 2002) surveyed and reviewed integration of the strategic and tactical models in the numerous researches. Badri et al. (2013) proposed a new SCND mathematical model considering different time resolutions for tactical and strategic decisions. Salema et al. (2010) integrated strategic and tactical decisions in a novel SCND model. Because of existing a research gap and of course suggestion of previous researchers, in this study, it is tried to regard tactical decisions during the making of strategic decisions.

Today one of the basic features of SCND is uncertainty, lack of the exact and clear around information and dynamic environment. A real supply chain should be operated in an uncertain environment and disregarding any effects of uncertainty causes to design a worthless supply chain (Xu and Zhai 2008) and also as (Nenes and Nikolaidis 2012) said coping dynamically with variations is essential for any remanufacturing enterprise. The crisp methods cannot solve problem with decision-makers’ uncertainties, ambiguities and vagueness (Kulak and Kahraman 2005). Some methods are applied to overcome it, such as stochastic programming and fuzzy optimization. Stochastic programming is used when the parameters (for example costs and demands) are stochastic and they may fluctuate widely (Snyder 2006). The reader is referred to some papers which solved SCND problems using stochastic programming such as: (Santoso et al. 2005; Ramezani et al. 2013; Pishvaee et al. 2009) and so on. In the fuzzy environment, it is assumed that the related parameters, coefficient, objective goals and constraints have ambiguous. Baykasoǧlu and Göçken (2008) classified fuzzy mathematical programming models according to the components which are aspiration values of the objectives (F), the right hand side value of the constraints (b), the coefficients of the objectives (c) and the coefficients of the constraints (A) and their combinations (in total, there are fifteen types of fuzzy mathematical programming models according to the fuzzy components). Using deterministic and stochastic models may not cause to fully satisfactory consequences and these drawbacks can be removed by application of fuzzy models (Aliev et al. 2007) and overcome the problem of imprecision that usually occurs in supply chain (Sarkar and Mohapatra 2006). Moreover, computational efficiency and flexibility in fuzzy mathematical programming is more than the deterministic and stochastic programming techniques (Liang 2011). In addition, one of the main reasons to use fuzzy theory in SCM problems is unexpected variations throughout the supply chain (Sadeghi et al. 2014) and as (Hasani et al. 2012) said the uncertainty issue is more important in reverse and closed loop supply chain network design, because of reverse material flows have the inherent uncertainty in comparison to forward material flows and quantity and quality of the returned products are usually uncertain.

A significant shortcoming of the previous works of the SCND in fuzzy environment is that they have ignored fuzziness of decision variables. They suppose that the parameters are fuzzy but it is assumed that decision variables are crisp. Fuzziness of decision variables in the supply chain can lead to have more flexibility in the later decisions in each element of the supply chain (Kabak and Ülengin 2011). This omission appeared anomalous considering tactical and strategic level decisions. By considering of ambiguous for decision variables of the tactical decisions, more flexible and efficient strategic decisions can be made in which is closer to the real-world situations. Moreover, quantity of shipments in SCM is always uncertain and it is hard to estimate these parameters (Qin and Ji 2010; Fazlollahtabar et al. 2012).

As authors best knowledge this study is the first research considering fuzziness of decision variables in supply chain network design problems. In the other fields the variables are handled as fuzzy numbers, for example (Fazlollahtabar et al. 2012) proposed a vehicle routing problem with fuzzy decisions and also (Kabak and Ülengin 2011) considered a mathematical model containing the resources allocation and outsourcing decisions which the two decision variables are considered to be fuzzy such as the input parameters. A resources management problem with social and environmental factors presented by (Tsakiris and Spiliotis 2004), a multi-item solid transportation problem proposed by (Giri et al. 2015) and inventory models for items with shortage backordering stated by (Mahata and Goswami 2013) are other researches which include fuzzy decision variables in the other fields.

The main contributions and advantages of this research that distinguishes this paper from the presented existing ones in the related literature are listed as follows:

  • Considering suppliers and evaluation and selection of them: The supplier selection has been acknowledged an important and considerable challenge in supply chain and it has a growing effect on the success or failure of a business (Bevilacqua et al. 2006). Supplier selection problem receives attention of so many researchers; so that (Chai et al. 2012) selected and reviewed 123 journal articles and (Igarashi et al. 2013) examined 60 green supplier selection articles.

  • Presenting a novel closed loop multi-echelon supply chain network design model which considers tactical and strategic decision levels which this gap is suggested as a necessary and significant future research (Pishvaee and Razmi 2012; Govindan et al. 2015).

  • Regarding the life cycle assessment of a product (cradle-to-grave).

  • Considering transportation mode selection: recently (Govindan et al. 2015) reviewed 328 papers about reverse logistics and closed loop supply chain and said that these decisions are distinguished as a remarkable gap and future opportunity.

  • Offering an efficient programming model which can be used in a real cases such as automotive industry (Olugu and Wong 2012), computer (Kusumastuti et al. 2008), outdated products (such as IC chips and mobile phones) (Yang et al. 2010), plastics (Pohlen and Farris 1992), carpet (Biehl et al. 2007), battery (Fernandes, Gomes-Salema, and Barbosa-Povoa 2010; Kannan, Sasikumar, and Devika 2010, Sasikumar and Haq 2011), medical needle and syringe (Pishvaee and Razmi 2012), Waste electrical and electronic equipment recycling (Nagurney and Toyasaki 2005; Tsai and Hung 2009), copiers (Krikke 2011) and in a wide various of process industries including chemicals, food, rubber, and plastics (French and LaForge 2006).

  • Computational analysis is provided by using a hospital industrial case study to present the significance of the presented model as well as the efficiency of the proposed solution method.

  • Considering the parameters and the decision variables as a triangular fuzzy number: This is disregarded by the previous researchers, while some authors emphasis that the variables should be assumed with ambiguous such as (Qin and Ji 2010; Kabak and Ülengin 2011; Fazlollahtabar et al. 2012).

The remainder of this paper is organized as follows. At first, a literature review of supply chain network design using fuzzy mathematical programming is presented in “Literature review of SCND using fuzzy mathematical programming”. The proposed supply chain network design is described in “The proposed closed loop supply chain network design”. Then in “Formulation of the model”, indices, parameters, decision variables are introduced and the formulation of the proposed SCND model is stated. “The proposed fuzzy optimization approach” contains a new fuzzy optimization approach and its applications. In “Numerical examples” several numerical examples are discussed to verify the proposed approach and model. After that some comparisons are presented to show the priority of proposed approach. “Case study and managerial implications” consider and analysis a real case study and the differences of the proposed method with other approaches show the advantage of the proposed method and then some managerial insights are drawn. Finally, the concluding remarks and the future study directions are expressed in “Conclusion”.

Literature review of SCND using fuzzy mathematical programming

Generally, the supply chain network design studies in the fuzzy environment can be categorized in three following classes:

  • Forward supply chain network design using fuzzy mathematical programming.

  • Reverse logistics network design using fuzzy mathematical programming.

  • Closed loop supply chain network design using fuzzy mathematical programming.

Forward supply chain network design using fuzzy mathematical programming

In the forward supply chain network models, the components and raw materials are purchased from suppliers and the products are manufactured in the plants and then they are shipped to downstream facilities (likely warehouses, distribution center (DC) and retailers and certainly the customers) and on the other hand the information and financial flows are given back to the upstream echelons. Some of the parameters such as demands, capacities and cost are handled as fuzzy numbers. Some of the papers trying to optimize the forward supply chain network design using fuzzy mathematical programming can be seen in Table 1. In most of them, the decision variables are considered as crisp, only (Bashiri and Sherafati 2012) optimized a multi-product supply chain network design using a fuzzy optimization introduced by (Kumar et al. 2010). In that study, both of the decision variables and parameters are assumed as fuzzy values. Additionally just three of them integrate the transportation mode selection issues as tactical decisions with strategic network design decisions.

Table 1 Summary of supply chain network design literature in fuzzy environment
Full size table

Reverse logistics supply chain network design using fuzzy mathematical programming

If the products are returned to the manufactures in order to recycle, reuse, remanufacturing, the model is named “reverse logistics”. With reverse logistic activities, customer service level and competence of enterprises can be improved and the motivation and demands of customers are increased, because it provides a green image to the enterprises (Özceylan and Paksoy 2013a, b).

Thin part of literature is dedicated to this classification, these studies are presented briefly as follows.

Qin and Ji (2010) applied a fuzzy programming tool to design the product recovery network. That research is one of the first studies which regarded to logistics network design with product recovery in fuzzy environment. Three fuzzy programming models were formulated and a hybrid intelligent algorithm was designed to solve the proposed models.

Moghaddam (2015) developed a general reverse logistics network as a fuzzy multi-objective mathematical model. To find the Pareto optimal and solve the model, a simulation method is proposed and applied. Finally a real case study is adopted to evaluate and validate the model and the solution method.

Closed loop supply chain network design using fuzzy mathematical programming

If both of the forward and reverse flows are integrated simultaneously, the mode is known as “closed loop supply chain network”. In the following, some of the papers trying to optimize the closed loop supply chain network design using fuzzy mathematical programming are mentioned.

Pishvaee and Torabi (2010) presented a bi-objective possibilistic mixed-integer programming model to design a closed loop supply chain network. In that research, an interactive fuzzy solution method is proposed to solve the possibilistic optimization problem. Selim and Ozkarahan (2008) optimized a supply chain network design model using a new approach. In their study, objectives targets are handled as fuzzy but the parameters and right hand side of constraints are considered as crisp. The fuzzy objectives are minimization of total costs, minimization of plants and warehouses investment cost, and maximization of the total service level provided to the retailers. Zarandi et al. (2011) integrated (Selim and Ozkarahan 2008)’s model with backward flows and they assumed fuzziness for objectives targets and also crispness for parameters. In the mentioned research, the solution approach is similar to (Selim and Ozkarahan 2008)’s research and the proposed closed loop supply chain network is optimized by that approach. Pishvaee and Razmi (2012) used a multi-objective fuzzy mathematical programming to design a green supply chain network with forward and reverse flows. The proposed model minimizes the total cost and also minimizes the total environmental impact. The fuzzy model is transformed to the crisp equivalent auxiliary model using (Jiménez et al. 2007). Then the modified ε-constraint method and an interactive fuzzy solution approach are applied to solve the crisp problem. Finally, the proposed model and fuzzy optimization approach are applied in a real industrial case. Vahdani et al. (2012) presented a reliable closed loop supply chain as a bi-objective mathematical programming. A new hybrid solution approach (which is combination of robust optimization approach, queuing theory and fuzzy multi-objective programming) is applied to design the proposed reliable closed logistics network under uncertainty. Özkır and Başlıgil (2012) suggested a fuzzy multiple objective optimization model to a closed loop supply chain network design problem and various recovery processes. The considered objective functions are: maximizing the satisfaction levels of the closed loop supply chain stakeholders, sourced by sales and purchasing price, maximizing the fill rate of customer demands, maximizing the total profit. The proposed model is solved using Baron Solver and it also is validated. Özceylan and Paksoy (2013a, b) proposed a fuzzy multi-objective model to optimize a general closed loop supply chain network. In that research two objectives and the capacities, demands and reverse rates are uncertain and are assumed as fuzzy number to incorporate the logistics manager’s imprecise aspiration levels. They converted the model to the crisp equivalent and solved it. Subulan et al. (2014) developed a multi-objective and multi-product closed loop supply chain model for a real case study, i.e., the lead/acid battery. Fuzzy goal programming approach is applied to solve the presented model. One of the contributions of the mentioned research is considering a new objective function to maximize of “the collection of returned batteries covered by the opened facilities”.

Summary of supply chain network design literature is shown in Table 1. In Table 1 F, A, c, b and x are objective function target, coefficients of constraints, coefficients of the objectives, right hand side of constraints and decision variables, respectively. According to the presented literature and Table 1 some drawbacks are found in closed loop supply chain network design area, such as ambiguous of decision variables, considering of more echelons, making tactical decisions, regarding transportation mode selection and so on. As it was mentioned in end of “Introduction”, in this research it is tried to overcome these drawbacks and the suggestions of researchers. In this study, both forward and reverse flows are considered and moreover, strategic level decisions in a long-term horizon and tactical level decision in a medium term horizon are examined. In addition, it is more real because all of the parameters and decision variables are considered as triangular fuzzy numbers (it is a fully fuzzy model). We believe that by considering of tactical decision variables with fuzzy values the resulted strategic decisions will be more accurate according to the real-world conditions.

The proposed closed loop supply chain network design

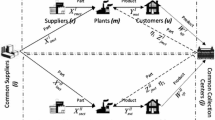
The concerned integrated closed loop supply chain network in this research is a multi-echelon, single product logistics network type including suppliers, plants, distribution centers and customer zones in forward flows and also collection centers and disposal center in revers flows.

As it is demonstrated in Fig. 1 the structure of the closed loop supply chain network contains both forward and reverse flows. The manufacturers purchase some of the components from suppliers and assemble the components and produce the products, and then products are transported to distribution centers (DCs) and to customers. In the reverse flow, customers give back the percentage of used products to collection centers (CCs). The collected products are disassembled in collection centers and they are retuned into the components. The rate of the old components (e.g., α  %) are reusable and are sold to plants by collection centers, and other (1−α) % are shipped to disposal, because they are not suitable for remanufacturing.

Fig. 1
figure 1

The structure of the proposed closed loop supply chain network

Full size image

The supplier selection problem is considered here, it has been acknowledged an important and considerable challenge in supply chain and it has a growing effect on the success or failure of a business (Bevilacqua et al. 2006). Supplier selection problem receives attention of so many researchers, so that (Chai et al. 2012) selected and reviewed 123 journal articles and (Igarashi et al. 2013) examined 60 green supplier selection articles. There are also several models considering supplier selection decisions such as (Torabi and Hassini 2008). We regard to this and location of the other facilities in the mathematical model.

The following assumptions are considered in the proposed SCND problem.

  • The long life of the components is more than the longevity of the products. So components of a used product can be reused in the other products.

  • All demands of customers should be satisfied.

  • There is a pull mechanism in the forward side of network while there is a push mechanism in the reverse side (Pishvaee and Torabi 2010).

  • There are different transportation modes in each link. Once a selection is made about the transport modes, a decision should be made regarding the type and size of the transportation unit (Dekker et al. 2012).

  • There is a single disposal.

  • Buying cost of components from collection centers includes buying and transportation costs.

  • Buying components from the collection centers is more economical than suppliers.

  • Collection cost consists of collection and disassemble of the product.

  • Some tactical decisions such as determination of transportation modes in each link, material flow quantity, etc. in the presence of strategic decisions are made.

Formulation of the model

Indices

s: set of suppliers s = 1,\(\ldots\), S; m: set of manufacturers/plants m = 1,\(\ldots\), M; d: set of distribution centers d = 1,\(\ldots\), D; c: set of customer zones c = 1,\(\ldots\), C; k: set of collection centers k = 1,\(\ldots\), K; t: transportation types t = 1,\(\ldots\), T.

Parameters

The parameters are assumed as fuzzy triangular numbers for example \(\tilde{f}_{m}\) is considered as (f1  m , f2  m , f3  m ).

\(\tilde{f}_{m}\): fixed or setup cost for making products in plant m. \(\tilde{g}_{d}\): fuzzy fixed cost for opening of distribution center d. \(\tilde{l}_{k}\): fuzzy fixed cost for opening of collection center k. \(\tilde{a}_{smt}\): fuzzy cost of buying and shipping components from supplier s to plant m with transportation mode t. \(\tilde{b}_{kmt}\): fuzzy cost of buying and shipping components from collection center k to plant m with transportation mode t. \(\tilde{\rho }_{m}\): fuzzy production cost of products by plant m \(\tilde{\eta }_{dct}\): products fuzzy distribution cost from distribution center d to customer zone c with transportation mode t. \(\tilde{\beta }_{mdt}\): fuzzy transportation cost of the manufactured products from plant m to distribution center d with transportation mode t. \(\tilde{\pi }_{k}\): fuzzy contractual cost relevant to collection and disassembling of returned products in collection center k. \(\tilde{\varepsilon }_{k}\): disposal related fuzzy cost for shipped unusable components from collection center k to disposal. \(\tilde{\gamma }_{m}\): fuzzy capacity of plant m. \(\tilde{\phi }_{d}\): fuzzy capacity of distribution center d. \(\tilde{\sigma }_{k}\): fuzzy capacity of collection center k. \(\tilde{\delta }_{c}\): fuzzy mean demand of customer zone c for products. \(\tilde{r}_{c}\): fuzzy rate of return (%) from customer zone c. \(\alpha\): mean disposal fraction.

Decision variables

The decision variables are assumed as fuzzy triangular numbers for example \(\tilde{x}_{smt}\) is considered as (x1 smt , x2 smt , x3 smt ).

\(\tilde{x}_{smt}\): fuzzy quantity of components shipped from supplier s to plant m with transportation mode t. \(\tilde{y}_{smt}\): fuzzy quantity of components shipped from collection center k to plant m with transportation mode t. \(\tilde{u}_{smt}\): fuzzy quantity of products shipped from plant m to distribution center d with transportation mode t. \(\tilde{v}_{dct}\): fuzzy quantity of products shipped from distribution center d to customer zone c with transportation mode t. \(\tilde{w}_{ck}\): fuzzy quantity of products shipped from customer zone c to collection center k. \(\tilde{p}_{k}\): fuzzy quantity of components shipped from collection center k to the disposal. \(\tilde{q}_{m}\): fuzzy quantity of product manufactured in plant m. n m : 1, if the plant m is opened, 0 otherwise. e d : 1, if the distribution center d is opened, 0 otherwise. o k : 1, if the collection center k is opened, 0 otherwise.

Formulation

According to above notations, the formulation of the discussed closed loop supply chain network design is as following:

$$\begin{aligned} \begin{array}{*{20}c} {\hbox{min} } & {TC} \\ \end{array} = & \sum\limits_{m} {\tilde{f}_{m} } n_{m} + \sum\limits_{d} {\tilde{g}_{d} } e_{d} + \sum\limits_{k} {\tilde{l}_{k} } o_{k} \\ & + \sum\limits_{s} {\sum\limits_{m} {\sum\limits_{t} {\tilde{a}_{smt} \tilde{x}_{smt} } } } + \sum\limits_{k} {\sum\limits_{m} {\sum\limits_{t} {\tilde{b}_{kmt} \tilde{y}_{kmt} } } } \\ & + \sum\limits_{m} {\tilde{\rho }_{m} \tilde{q}_{m} } \\ & + \sum\limits_{d} {\sum\limits_{c} {\sum\limits_{t} {\tilde{\eta }_{dct} \tilde{v}_{dct} } } } \\ & + \sum\limits_{m} {\sum\limits_{d} {\sum\limits_{t} {\tilde{\beta }_{mdt} \tilde{u}_{mdt} } } } \\ & + \sum\limits_{k} {\tilde{\varepsilon }_{k} \tilde{p}_{k} } \\ & + \sum\limits_{k} {\tilde{\pi }_{k} \sum\limits_{c} {\tilde{w}_{ck} } } \\ \end{aligned}$$
(1)
$$\begin{aligned} {\text{s}}.{\text{t}}. \hfill \\ \sum\limits_{k} {\sum\limits_{t} {\tilde{y}_{kmt} } } + \sum\limits_{s} {\sum\limits_{t} {\tilde{x}_{smt} } } \le n_{m} \gamma_{m} \;\;\;\forall m \hfill \\ \end{aligned}$$
(2)
$$\sum\limits_{m} {\sum\limits_{t} {\tilde{u}_{mdt} } } \le e_{d} \tilde{\phi }_{d} \;\;\;\forall d$$
(3)
$$\sum\limits_{c} {\tilde{w}_{ck} } \le o_{k} \tilde{\sigma }_{k} \;\;\;\forall k$$
(4)
$$\sum\limits_{k} {\sum\limits_{t} {\tilde{y}_{kmt} } } + \sum\limits_{s} {\sum\limits_{t} {\tilde{x}_{smt} } } \ge \tilde{q}_{m} \;\;\;\forall m$$
(5)
$$\tilde{q}_{m} \ge \sum\limits_{d} {\sum\limits_{t} {\tilde{u}_{mdt} } } \;\;\;\forall m$$
(6)
$$\sum\limits_{m} {\sum\limits_{t} {\tilde{u}_{mdt} } } = \sum\limits_{c} {\sum\limits_{t} {\tilde{v}_{cdt} } } \;\;\;\forall d$$
(7)
$$\sum\limits_{d} {\sum\limits_{t} {\tilde{v}_{cdt} } } \ge \tilde{\delta }_{c} \;\;\;\forall c$$
(8)
$$\sum\limits_{k} {\tilde{w}_{ck} } \ge \tilde{r}_{c} \tilde{\delta }_{c} \;\;\;\forall c$$
(9)
$$\sum\limits_{m} {\sum\limits_{t} {\tilde{y}_{kmt} } } = \sum\limits_{c} {\alpha \times \tilde{w}_{ck} } \;\;\;\forall k$$
(10)
$$\tilde{p}_{k} = \sum\limits_{c} {(1 - \alpha ) \times \tilde{w}_{ck} } \;\;\;\forall k$$
(11)
$$\begin{aligned} & n_{m} ,e_{d} ,o_{k} \varepsilon \, \{ 0, 1 {\text{\} }} \\ & \tilde{x}_{smt} , \, \tilde{y}_{kmt} , \, \tilde{u}_{mdt} , \, \tilde{v}_{dct} , \, \tilde{w}_{ck} , \, \tilde{p}_{k} \ge \, 0\;\;\;\forall m,d,s,k,c \\ \end{aligned}$$
(12)

The objective function is minimization of the total cost (1), the total cost includes sum of the fixed, buying, manufacturing, distribution, transportation, collection & disassemble and disposal costs, respectively. Constraint (2) limits the quantity of manufactured product based on capacity of the plants. Constraints (3) and (4) are similar to the constraint (2) and they restrict the transported shipments to DCs and collection centers, respectively, based on their capacities. According to constraint (5), the quantities of input components to plants should be larger than the used components in products because some of them are useless. Constraint (6) assures that the production should be more than or equal to the final products, because they may be not accepted by the quality control unit. Constraint (7) is similar to constraint (6) and it balances the quantity transported to DCs with the distributed quantity to customer zones by DCs. Constraint (8) ensures that all of the demands are satisfied. Constraint (9) guarantees that the used products are returned to the collection centers (Pishvaee and Razmi 2012). Constraint (10) assures balancing of components volume after disassembling the products between plant and collection center. The same constraint for the disposal and collection center is guaranteed by constraint (11). Constraint (12) defines decision variables types.

The proposed fuzzy optimization approach

In this section a new fuzzy optimization approach is proposed for the aforementioned supply chain configuration in a fuzzy environment based on (Lai and Hwang 1992)’s approach, (Torabi and Hassini 2008) (TH) and (Kabak and Ülengin 2011). It is worth to mention that in this approach decision variables will remain fuzzy triangular variables during optimization stages.

(Kabak and Ülengin 2011) considered a mathematical model containing the resources allocation and outsourcing decisions which only two decision variables are considered to be fuzzy such as the input parameters. The advantage of this current research in comparison to (Kabak and Ülengin 2011) is that, the proposed model is fully fuzzy programming and it is applied to minimize the total cost in a supply chain network design problem. As authors’ best knowledge, it is the first study which considerers SCND model containing fuzzy decision variables. The model presented by (Kabak and Ülengin 2011) is related to resources allocation and outsourcing decisions. Moreover, that model is extended to thirty objective function here, so the better solution can be find using this proposed approach.

(Torabi and Hassini 2008) presented a comprehensive supply chain master planning model which integrates the procurement, production and distribution plans. All of the parameters are handled as fuzzy number; however, the decision variables are assumed as crisp. (Torabi and Hassini 2008) proposed a novel solution approach in order to find an efficient compromise solution for a fuzzy multi-objective mixed-integer program with crisp decision variables.

None of the considered base papers regard to a supply chain network design problem.

In (Lai and Hwang 1992)’s approach, it is assumed that total objective function is a triangular fuzzy number \((\tilde{Z}^{l} ,\tilde{Z}^{m} ,\tilde{Z}^{r} )\), and \(\tilde{Z}^{m}\) should be minimized, (\(\tilde{Z}^{m} - \tilde{Z}^{l}\)) should be maximized and (\(\tilde{Z}^{r} - \tilde{Z}^{m}\)) should be minimized simultaneously to obtain better solution in the minimization problems (Torabi and Hassini 2008) used the (Lai and Hwang 1992)’s approach, and proposed interactive fuzzy programming with multiple objectives.

(Kabak and Ülengin 2011) presented a new approach to solve possibilistic linear programming with fuzzy decision variables. The authors introduced the entropy for profit objectives and tried to minimize this entropy while the profit objective should be maximized. The entropy is the difference between the upper bound and the lower bound of the profit objective. In the mentioned approach, (Kabak and Ülengin 2011) proposed two linear programming, named LP-1 and LP-2. In LP-1 it is assumed that fuzzy variables are as crisp variables and the problem is optimized twice. In the first, the fuzzy parameters are set at their right value of triangular fuzzy number. After optimization of a crisp model upper bound of objective function is obtained which is called \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z}\). In the second stage, the fuzzy parameters are set at their left value of triangular fuzzy number. Lower bound of objective function is obtained after optimization and is called \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{Z}\). The obtained values for objective function will be used to make two normalized measures presented in Eqs. (13) and (14).

$$\lambda _{1} = \frac{{z^{m} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }}$$
(13)
$$\lambda_{2} = 1 - \frac{{z^{r} - z^{l} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }}$$
(14)

where Z m is the median value of the fuzzy objective function, and λ 1 and λ 2 are the normalized measures which will be used for the LP-2 model. It is formulated as follows:

$$\begin{aligned} LP - 2 \hfill \\ \hbox{max} \mathop {}\nolimits_{{}}^{{}} \mathop {}\nolimits_{{}}^{{}} z = \lambda + \delta (\lambda_{1} + \lambda_{2} ) \hfill \\ s.t.\mathop {}\nolimits_{{}}^{{}} \mathop {}\nolimits_{{}}^{{}} \mathop {}\limits_{{}} \lambda \le \lambda_{1} = (z^{m} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} )/(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} ) \hfill \\ \mathop {}\nolimits_{{}}^{{}} \mathop {}\nolimits_{{}}^{{}} \mathop {}\nolimits_{{}}^{{}} \mathop {}\limits_{{}} \lambda \le \lambda_{2} = ((\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} ) - (z^{r} - z^{l} ))/(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} ) \hfill \\ \end{aligned}$$
(15)

where δ is a small number to give priority to the first part.

The proposed method in this research is more complete than (Kabak and Ülengin 2011)’s approach (hereafter KÜ approach), because in this study all parameters and decision variables are assumed fuzzy.

In this paper, based on the introduced three objective functions in (Lai and Hwang 1992)’s approach, thirty objective functions are proposed because of the fuzziness of decision variables expressed as following.

$$\begin{array}{*{20}c} {\hbox{min} } & {H_{i,k} = c_{i} \cdot x_{k} } \\ \end{array} \;\;\;\begin{array}{*{20}c} {i = 1,2,3} & {\;k = 1,2,3} \\ \end{array}$$
(16)
$$\begin{array}{*{20}c} {\hbox{min} } & {H_{i - j,k} = (c_{i} - c_{j} ) \cdot x_{k} } \\ \end{array} \;\;\;\begin{array}{*{20}c} {i = 3} & {j = 1,2} & {k = 1,2,3} \\ \end{array}$$
(17)
$$\begin{array}{*{20}c} {\hbox{min} } & {H_{i,k - l} = c_{i} } \\ \end{array} \cdot (x_{k} - x_{l} )\;\;\;\begin{array}{*{20}c} {i = 1,2,3} & {k = 3} & {l = 1,2} \\ \end{array}$$
(18)
$$\begin{array}{*{20}c} {\hbox{min} } & {H_{i - j,k - l} = (c_{i} - c_{j} )} \\ \end{array} \cdot (x_{k} - x_{l} )\;\;\;\begin{array}{*{20}c} {i = k = 3} & {j = l = 1,2} \\ \end{array}$$
(19)
$$\begin{array}{*{20}c} {\hbox{max} } & {H_{i - j,k} = (c_{i} - c_{j} ) \cdot x_{k} } \\ \end{array} \;\;\;\begin{array}{*{20}c} {i = 2} & {j = 1} & {k = 1,2,3} \\ \end{array}$$
(20)
$$\begin{array}{*{20}c} {\hbox{max} } & {H_{i,k - l} = c_{i} \cdot } \\ \end{array} (x_{k} - x_{l} )\;\;\;\begin{array}{*{20}c} {i = 1,2,3} & {k = 2} & {l = 1} \\ \end{array}$$
(21)
$$\begin{array}{*{20}c} {\hbox{max} } & {H_{i - j,k - l} = (c_{i} - c_{j} ) \cdot } \\ \end{array} (x_{k} - x_{l} )\;\;\;\begin{array}{*{20}c} {i = k = 2} & {j = l = 1} \\ \end{array}$$
(22)

where H = C·X and also C = (c 1, c 2, c 3) and X = (x 1, x 2, x 3) are triangular fuzzy numbers. For example, H 2−1,1 will be constructed as Eq. (23):

$$\begin{aligned} \begin{array}{*{20}c} {\hbox{min} } & {H_{2 - 1,1} } \\ \end{array} & = \sum\limits_{m} {(f2_{m} - f1_{m} )} \times n_{m} \\ & + \sum\limits_{d} {(g2_{d} - g1_{d} )} \times e_{d} \\ & + \sum\limits_{k} {(l2_{k} - l1_{k} )} \times o_{k} \\ & + \sum\limits_{s} {\sum\limits_{m} {\sum\limits_{t} {(a2_{smt} - a1_{smt} ) \times x1_{smt} } } } \\ & + \sum\limits_{k} {\sum\limits_{m} {\sum\limits_{t} {(b2_{kmt} - b1_{kmt} ) \times y1_{kmt} } } } \\ & + \sum\limits_{m} {(\rho 2_{m} - \rho 1_{m} ) \times q1_{m} } \\ & + \sum\limits_{d} {\sum\limits_{c} {\sum\limits_{t} {(\eta 2_{dct} - \eta 1_{dct} ) \times v1_{dct} } } } \\ & + \sum\limits_{m} {\sum\limits_{d} {\sum\limits_{t} {(\beta 2_{mdt} - \beta 1_{mdt} ) \times u1_{mdt} } } } \\ & + \sum\limits_{k} {(\varepsilon 2_{k} - \varepsilon 1_{k} ) \times p1_{k} } \\ & + \sum\limits_{k} {(\pi 2_{k} - \pi 1_{k} )\sum\limits_{c} {w1_{ck} } }. \\ \end{aligned}$$
(23)

Some of aforementioned objective functions can be deleted because some of them have the same direction.

Then, a linear membership function is defined for each objective and the problem continues as follows based on TH approach:For minimization objectives:

$$\mu_{g} = \left\{ {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} {if} & {H_{i,k} < H_{i,k}^{p} } \\ \end{array} } \\ {\frac{{H_{i,k}^{n} - H_{i,k} }}{{H_{i,k}^{n} - H_{i,k}^{p} }}} & {\begin{array}{*{20}c} {if} & {H_{i,k}^{p} \le H_{i,k} \le } \\ \end{array} } \\ 0 & {\begin{array}{*{20}c} {if} & {H_{i,k} > H_{i,k}^{n} } \\ \end{array} } \\ \end{array} } \right.H_{i,k}^{n} \;\;\;g = 1, \ldots , 9$$
(24)
$$\mu_{g} = \left\{ {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} {if} & {H_{i - j,k} < H_{i - j,k}^{p} } \\ \end{array} } \\ {\frac{{H_{i - j,k}^{n} - H_{i - j,k} }}{{H_{i - j,k}^{n} - H_{i - j,k}^{p} }}} & {\begin{array}{*{20}c} {if} & {H_{i - j,k}^{p} \le H_{i - j,k} \le } \\ \end{array} } \\ 0 & {\begin{array}{*{20}c} {if} & {H_{i - j,k} > H_{i - j,k}^{n} } \\ \end{array} } \\ \end{array} } \right.H_{i - j,k}^{n} \;\;\;g = 10, \ldots , 1 5$$
(25)
$$\mu_{g} = \left\{ {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} {if} & {H_{i,k - l} < H_{i,k - l}^{p} } \\ \end{array} } \\ {\frac{{H_{i,k - l}^{n} - H_{i,k - l} }}{{H_{i,k - l}^{n} - H_{i,k - l}^{p} }}} & {\begin{array}{*{20}c} {if} & {H_{i,k - l}^{p} \le H_{i,k - l} \le } \\ \end{array} } \\ 0 & {\begin{array}{*{20}c} {if} & {H_{i,k - l} > H_{i,k - l}^{n} } \\ \end{array} } \\ \end{array} } \right.H_{i,k - l}^{n} \;\;\;g = 1 6, \ldots , 2 1$$
(26)
$$\mu_{g} = \left\{ {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} {if} & {H_{i - j,k - l} < H_{i - j,k - l}^{p} } \\ \end{array} } \\ {\frac{{H_{i - j,k - l}^{n} - H_{i - j,k - l} }}{{H_{i - j,k - l}^{n} - H_{i - j,k - l}^{p} }}} & {\begin{array}{*{20}c} {if} & {H_{i - j,k - l}^{p} \le H_{i - j,k - l} \le } \\ \end{array} } \\ 0 & {\begin{array}{*{20}c} {if} & {H_{i - j,k - l} > H_{i - j,k - l}^{n} } \\ \end{array} } \\ \end{array} } \right.H_{i - j,k - l}^{n} \;\;\;g = 2 2, 2 3$$
(27)

where \(H_{i,k}^{n}\), \(H_{i - j,k}^{n}\), \(H_{i,k - l}^{n}\) and \(H_{i - j,k - l}^{n}\) are maximum of the Eqs. (16, 17, 18, 19) and \(H_{i,k}^{p}\), \(H_{i - j,k}^{p}\), \(H_{i,k - l}^{p}\) and \(H_{i - j,k - l}^{p}\) are minimum of them, respectively.

For maximization objectives:

$$\mu_{g} = \left\{ {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} {if} & {H_{i - j,k} > H_{i - j,k}^{p} } \\ \end{array} } \\ {\frac{{H_{i - j,k}^{{}} - H_{i - j,k}^{n} }}{{H_{i - j,k}^{p} - H_{i - j,k}^{n} }}} & {\begin{array}{*{20}c} {if} & {H_{i - j,k}^{n} \le H_{i - j,k} \le } \\ \end{array} } \\ 0 & {\begin{array}{*{20}c} {if} & {H_{i - j,k} < H_{i - j,k}^{n} } \\ \end{array} } \\ \end{array} } \right.H_{i - j,k}^{p} \;\;\;g = 2 4, \ldots , 2 6$$
(28)
$$\mu_{g} = \left\{ {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} {if} & {H_{i,k - l} > H_{i,k - l}^{p} } \\ \end{array} } \\ {\frac{{H_{i,k - l} - H_{i,k - l}^{n} }}{{H_{i,k - l}^{p} - H_{i,k - l}^{n} }}} & {\begin{array}{*{20}c} {if} & {H_{i,k - l}^{n} \le H_{i,k - l} \le } \\ \end{array} } \\ 0 & {\begin{array}{*{20}c} {if} & {H_{i,k - l} < H_{i,k - l}^{n} } \\ \end{array} } \\ \end{array} } \right.H_{i,k - l}^{p} \;\;\;g = 2 7, \ldots , 2 9$$
(29)
$$\mu_{g} = \left\{ {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} {if} & {H_{i - j,k - l} > H_{i - j,k - l}^{p} } \\ \end{array} } \\ {\frac{{H_{i - j,k - l} - H_{i - j,k - l}^{n} }}{{H_{i - j,k - l}^{p} - H_{i - j,k - l}^{n} }}} & {\begin{array}{*{20}c} {if} & {H_{i - j,k - l}^{n} \le H_{i - j,k - l} \le } \\ \end{array} } \\ 0 & {\begin{array}{*{20}c} {if} & {H_{i - j,k - l} < H_{i - j,k - l}^{n} } \\ \end{array} } \\ \end{array} } \right.H_{i - j,k - l}^{p} \;\;\;g = 30$$
(30)

where \(H_{i - j,k}^{n}\),\(H_{i,k - l}^{n}\) and \(H_{i - j,k - l}^{n}\) are minimum of the (20)-(22) and \(H_{i - j,k}^{p}\),\(H_{i,k - l}^{p}\) and \(H_{i - j,k - l}^{p}\) are maximum of them, respectively.

Hence, the problem is performed as follows:

$$\begin{aligned} \hbox{max} \;\;\;\lambda = \gamma \lambda_{0} + (1 - \gamma )\sum\nolimits_{g} {\theta_{g} \cdot \mu_{g} } \hfill \\ s.t.\;\;\;\lambda_{0} \le \mu_{g} \;\;\;g = 1, \ldots ,30 \hfill \\ \end{aligned}$$
(31)
$$\sum\limits_{k} {\sum\limits_{t} {y1_{kmt} } } + \sum\limits_{s} {\sum\limits_{t} {x1_{smt} } } \le n_{m} \gamma 1_{m} \;\;\;\forall m$$
(32)
$$\sum\limits_{k} {\sum\limits_{t} {y2_{kmt} } } + \sum\limits_{s} {\sum\limits_{t} {x2_{smt} } } \le n_{m} \gamma 2_{m} \;\;\;\forall m$$
(33)
$$\sum\limits_{k} {\sum\limits_{t} {y3_{kmt} } } + \sum\limits_{s} {\sum\limits_{t} {x3_{smt} } } \le n_{m} \gamma 3_{m} \;\;\;\forall m$$
(34)
$$\sum\limits_{m} {\sum\limits_{t} {u1_{mdt} } } \le e_{d} \phi 1_{d} \;\;\;\forall d$$
(35)
$$\sum\limits_{m} {\sum\limits_{t} {u2_{mdt} } } \le e_{d} \phi 2_{d} \;\;\;\forall d$$
(36)
$$\sum\limits_{m} {\sum\limits_{t} {u3_{mdt} } } \le e_{d} \phi 3_{d} \;\;\;\forall d$$
(37)
$$\sum\limits_{c} {w1_{ck} } \le o_{k} \sigma 1_{k} \;\;\;\forall k$$
(38)
$$\sum\limits_{c} {w2_{ck} } \le o_{k} \sigma 2_{k} \;\;\;\forall k$$
(39)
$$\sum\limits_{c} {w3_{ck} } \le o_{k} \sigma 3_{k} \;\;\;\forall k$$
(40)
$$\sum\limits_{k} {\sum\limits_{t} {y1_{kmt} } } + \sum\limits_{s} {\sum\limits_{t} {x1_{smt} } } \ge q1_{m} \;\;\;\forall m$$
(41)
$$\sum\limits_{k} {\sum\limits_{t} {y2_{kmt} } } + \sum\limits_{s} {\sum\limits_{t} {x2_{smt} } } \ge q2_{m} \;\;\;\forall m$$
(42)
$$\sum\limits_{k} {\sum\limits_{t} {y3_{kmt} } } + \sum\limits_{s} {\sum\limits_{t} {x3_{smt} } } \ge q3_{m} \;\;\;\forall m$$
(43)
$$q1_{m} \ge \sum\limits_{d} {\sum\limits_{t} {u1_{mdt} } } \;\;\;\forall m$$
(44)
$$q2_{m} \ge \sum\limits_{d} {\sum\limits_{t} {u2_{mdt} } } \;\;\;\forall m$$
(45)
$$q3_{m} \ge \sum\limits_{d} {\sum\limits_{t} {u3_{mdt} } } \;\;\;\forall m$$
(46)
$$\sum\limits_{m} {\sum\limits_{t} {u1_{mdt} } } = \sum\limits_{c} {\sum\limits_{t} {v1_{cdt} } } \;\;\;\forall d$$
(47)
$$\sum\limits_{m} {\sum\limits_{t} {u2_{mdt} } } = \sum\limits_{c} {\sum\limits_{t} {v2_{cdt} } } \;\;\;\forall d$$
(48)
$$\sum\limits_{m} {\sum\limits_{t} {u3_{mdt} } } = \sum\limits_{c} {\sum\limits_{t} {v3_{cdt} } } \;\;\;\forall d$$
(49)
$$\sum\limits_{d} {\sum\limits_{t} {v1_{cdt} } } \ge \delta 1_{c} \;\;\;\forall c$$
(50)
$$\sum\limits_{d} {\sum\limits_{t} {v2_{cdt} } } \ge \delta 2_{c} \,\;\;\forall c$$
(51)
$$\sum\limits_{d} {\sum\limits_{t} {v3_{cdt} } } \ge \delta 3_{c} \;\;\;\forall c$$
(52)
$$\sum\limits_{d} {\sum\limits_{t} {v1_{cdt} } } \ge \delta 1_{c} \;\;\;\forall c$$
(53)
$$\sum\limits_{d} {\sum\limits_{t} {v2_{cdt} } } \ge \delta 2_{c} \;\;\;\forall c$$
(54)
$$\sum\limits_{d} {\sum\limits_{t} {v3_{cdt} } } \ge \delta 3_{c} \;\;\;\forall c$$
(55)
$$\sum\limits_{m} {\sum\limits_{t} {y1_{kmt} } } = \sum\limits_{c} {\alpha \times w1_{ck} } \;\;\;\forall k$$
(56)
$$\sum\limits_{m} {\sum\limits_{t} {y2_{kmt} } } = \sum\limits_{c} {\alpha \times w2_{ck} } \;\;\;\forall k$$
(57)
$$\sum\limits_{m} {\sum\limits_{t} {y3_{kmt} } } = \sum\limits_{c} {\alpha \times w3_{ck} } \;\;\;\forall k$$
(58)
$$p1_{k} = \sum\limits_{c} {(1 - \alpha ) \times w1_{ck} } \;\;\;\forall k$$
(59)
$$p2_{k} = \sum\limits_{c} {(1 - \alpha ) \times w2_{ck} } \;\;\;\forall k$$
(60)
$$p3_{k} = \sum\limits_{c} {(1 - \alpha ) \times w3_{ck} } \;\;\;\forall k$$
(61)
$$x1_{smt} \le x2_{smt} \le x3_{smt} \;\;\;\forall s,m,t$$
(62)
$$y1_{kmt} \le y2_{kmt} \le y3_{kmt} \;\;\;\forall k,m,t$$
(63)
$$u1_{mdt} \le u2_{mdt} \le u3_{mdt} \;\;\;\forall m,d,t$$
(64)
$$v1_{smt} \le v2_{smt} \le v3_{smt} \;\;\;\forall d,c,t$$
(65)
$$w1_{ck} \le w2_{ck} \le w3_{ck} \;\;\;\forall c,k$$
(66)
$$p1_{k} \le p2_{k} \le p3_{k} \;\;\;\forall k$$
(67)
$$n_{m} ,e_{d} ,o_{k} \varepsilon \left\{ {0,1} \right\}\;\;\;\forall m,d,k$$
(68)
$$\begin{aligned} & x1_{smt} , \, x2_{smt} , \, x3_{smt} , \, y1_{kmt} , \, y2_{kmt} , \, y3_{kmt} , \\ & u1_{mdt} , \, u2_{mdt} , \, u3_{mdt} ,v1_{dct} , \, v2_{dct} , \, v3_{dct} , \, \\ & w1_{ck} , \, w2_{ck} , \, w3_{ck} , \, p1_{ke} , \, p2_{ke} , \, p3_{ke} \ge \, 0\;\;\;\forall m,d,k,s,c \\ \end{aligned}$$
(69)

where λ is total satisfaction degree and indicates the final objective function of the proposed model, μ g is the satisfaction degree of the mentioned objective functions and λ 0 is the minimum satisfaction degree of objectives. γ and θ g denote coefficient of compensation and importance of corresponding objective, respectively, and they will be determined according to the decision maker preference \(\left( {\sum\limits_{g} {\theta _{g} = 1} } \right)\).

Based on the introduced approach, in the current model, there is an objective function while 30 + 3 × (3 m + 2d + 3 k + 2c) + (number of fuzzy decision variables) are taken into account. The problem involves (s × m × t + k × m × t + m × d × t + d × c × t + c × k + k + m) fuzzy decision variables and (m + d + k) binary variables.

Numerical examples

In this section, several hypothetical numerical examples are analyzed to verify the model and the application of the proposed fuzzy optimization method. In the first example, it is assumed that there are two potential locations for plants, two potential locations for DCs, two potential locations for collection centers, two suppliers, five customer zones and a disposal. The shipments are transported with three transportation modes. The parameters are simulated by random numbers which some of them have been reported in Tables 2, 3, 4. The first example includes 80 fuzzy decision variables, 6 binary variables and 188 constraints.

Table 2 Demands of customers in the first numerical example
Full size table
Table 3 Manufacturing cost in the first numerical example
Full size table
Table 4 Opening fixed cost of distribution centers in the first numerical example
Full size table

The first numerical example is modeled and solved using proposed fuzzy mathematical programming. Firstly the membership functions are obtained and they are set in the problem. For example, for H 2,2 the following values are computed.

$$H_{2,2}^{n} = 437417.1$$
(69)
$$H_{2,2}^{p} = 91672.82$$
(70)
$$\mu_{5} = \left\{ {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} {if} & {H_{2,2} < 91672.82} \\ \end{array} } \\ {\frac{{437417.1 - H_{2,2} }}{437417.1 - 91672.82}} & {\begin{array}{*{20}c} {if} & {91672.82 \le H_{2,2} \le } \\ \end{array} } \\ 0 & {\begin{array}{*{20}c} {if} & {H_{2,2} > 437417.1} \\ \end{array} } \\ \end{array} } \right.437417.1$$
(71)

Finally the optimal configuration has been depicted in Fig. 2.

Fig. 2
figure 2

The optimal supply chain network of the example by the proposed approach

Full size image

The first numerical example is optimized using KÜ and TH approaches and Table 5 illustrates the obtained results by the mentioned approaches. For this example related parameters for the problem have been assumed as following; γ = 0.1, also θ 1 = θ 2 = θ 3 = 0.3 and the others are 0.0037. As it is shown in Table 5, the minimization objectives in the proposed approach are less than KÜ method and the maximization objectives are more.

Table 5 Some optimal values of decision variables using proposed, KÜ and TH approaches and crisp parameters
Full size table

Also Table 5 confirms that the proposed method has obtained more appropriate results especially in total satisfaction degree in comparison to both KÜ and TH methods.

Moreover the comparison of results of the proposed approach and TH approach shows that the transportation (and distribution) cost of TH method is further than the proposed approach. The reason of this increase is that the activated links and also facilities are greater in exact approach (as it is illustrated in Fig. 3). It should be noted that in fuzzy environment the flexibility is further and solution space is wider, consequently the superior solution can be find. This can be recognized by comparison of Figs. 2 and 3. In addition, as it was mentioned if decisions are assumed fuzzy in tactical level, more flexibility and proper decisions can be made for the strategic decisions. To do more sensitivity anlysis of the proposed research, it is tried to consider fuzzy parameters with least fuzziness, so each parameter were set as (a − 0.01, a, a + 0.01) and the problem was optimized using our proposed method. Then the problem was solved by classic approach (with crisp values of parameters and variables).

Fig. 3
figure 3

The optimal supply chain network by crisp decision variables (TH method)

Full size image

Table 6 shows the results and the comparisons confirm that the proposed approach in the scenario in which parameters are handled with least fuzziness can obtain similar results of classic approach with crisp parameters and variables. Also the results of Table 5 show that considering of ambiguous for parameters will lead to have a network with least network links and transportation modes. Moreover comparisons of Table 6 confirm that results of the proposed approach contain results of the problem with crisp parameters.

Table 6 Comparison of obtained results using the proposed approach with least fuzziness and classic method
Full size table

More examples are considered to assess the usefulness and performance of the proposed model and the solution method. Four numerical examples with different dimensions are generated and then optimized using proposed and KÜ approaches. The numerical examples and obtained total cost are illustrated in Table 7. As it is shown in Table 1 in all of the numerical examples, the total costs obtained by proposed approach have more appropriate values than the KÜ approach significantly. Moreover, the differences between upper and lower bounds (the entropies) in proposed approach are less than the corresponding values in KÜ approach.

Table 7 The numerical examples with the dimension and the total cost using proposed approach and KÜ approach
Full size table

Case study and managerial implications

If the supply chain network is designed properly and accurately and the entities are integrated and work cooperatively, managerial capabilities are promoted and some of the critical and major problems can be solved. It means the supply chain network design plays a vital and crucial role in overall performance of the supply chain. So in this study it is tried to develop a novel solution methodology in closed loop supply chain network configuration models in order to optimize the network configuration and help to the managers. This research can help to the stakeholders and improve the whole of the supply chain. Therefore, to verify this claim, in this section, the proposed supply chain network design model and the proposed solution algorithm are implemented for a real case study adapted from (Soleimani and Kannan 2015). It is related to Mehran Hospital Industries (Mehran Teb Med Co., http://www.Mehranmed.com), the first manufacturer of hospital industrial in Iran with 50 years of experience. Some hospital furniture such as beds, stretchers, trolleys, and so on are manufactured and sold to the hospitals, and after a while these used furniture are collected from the hospitals, so the network should be considered as closed loop.

Since the proposed model is single product problem, so just hospital bed is considered here as a product.

After formulation and optimization of the studied case, the optimal solutions obtained by the proposed, TH and KÜ approaches can be seen in Table 8. In the proposed and KÜ approaches, since the solutions are obtained as a triangular fuzzy number (a, b, c), so they are converted to a single number by centroid method (\(\frac{a + b + c}{3}\)) (Lam et al. 2010), to compare of the results obtained by various approaches.

Table 8 Total cost in the case study obtained using proposed, KÜ and TH approaches (in millions of Rials)
Full size table

As it is seen in the obtained solutions, the proposed approach can present the better solutions and proposed supply chain network design model and also the proposed solution algorithm are confirmed in a real case study.

The main suggestion to the managers is extension of the capacity of the reverse supply chain to improve profits. Moreover, another recommendation is encouraging the customers to sell/replace their used products to the manufacturer. This improves the current rate of return of products and reduces the network total cost.

Finally, it can be concluded that the proposed hybrid approach provides an acceptable and satisfactory performance in real cases of a hospital furniture leader company that can prove and confirm its applicability in real-world situations. Moreover, comparison results confirm that by consideration of fuzzy tactical decision variables, total transportation cost and other related results will be improved because of flexibility of decisions for strategic stage.

Conclusion

This study proposes a novel fuzzy programming model to formulate a closed loop supply chain network design problem integrating the strategic and tactical decisions in a multi-echelon supply chain network. Moreover fuzzy programming procedure has been developed to optimize of the proposed closed loop supply chain network design model. In the proposed fuzzy approach, all parameters and decision variables (except binary variables) have ambiguous and it is fully fuzzy programming. As some researches mentioned, since we consider strategic level decisions, hence it is more satisfactory that the decision variables are not handled as crisp and certain and they are assumed as fuzzy triangular numbers. The environment is uncertain, fuzziness of decision variables in the supply chain models causes that the presented solutions have more flexibility and the managers can make more satisfactory decisions especially in tactical and strategic plans. Some numerical example are applied to verify the proposed fuzzy approach and the comparisons of results in the examples indicate that the proposed method is very promising fuzzy optimization approach because it presents more appropriate results than the previous approaches. Moreover comparison results confirm that by consideration of fuzzy tactical decision variables, total transportation cost and other related results will be improved because of flexibility of decisions for strategic stage.

This research can help to the stakeholders and improve the whole of the supply chain. The proposed model and also methodology are expected to provide an important guide to supply chain managers in making their decisions, taking into account the fuzziness of decision variables as it is shown in a real studied case. In the case study such as the numerical instances, the developed hybrid algorithm can achieve most appropriate solutions in comparison with the TH and KÜ.

As future research extension of the proposed model and designing of a dynamic closed loop supply chain network and also a sustainable supply chain network considering environmental and social aspects are suggested. Moreover, the researchers can apply the efficient proposed approach to solve the fully fuzzy mathematical programming models due to its computational advantages.