Effects of concrete parameters in the lateral stiffness of reinforced concrete squat walls

Abstract

The basis for the effective stiffness values or expressions and their applicability to nuclear power plant elements is not clearly presented in current seismic standards. This paper studies the effective stiffness of reinforced concrete (RC) squat walls under lateral loads. RC squat walls have height-to-length ratios less than or equal to 2. Prediction of the seismic response and proper capturing of the effective stiffness of squat walls are a challenging task, since these walls exhibit a shear-dominated behavior with strong coupling between shear and flexure responses. Finite-element models of several RC squat walls are developed using the commercial software Abaqus. The main objective of these models is to predict the lateral stiffness of RC squat walls appropriately and to identify the parameters that have main influence in the lateral stiffness of these walls. The results from analytical modeling are compared with the results of experimental tests available in the literature. Available expressions in current seismic standards and in the literature for the calculation of effective stiffness for RC squat walls are also evaluated. Key parameters influencing the effective stiffness are identified during the nonlinear analyses and from existing experimental data.

Introduction

Reinforced concrete (RC) shear walls with height-to-length ratios less than or equal to two are commonly used in nuclear power plants buildings as part of their lateral-load-resisting system. These walls are known as squat or short walls. Three types of failure can be found in squat RC walls: diagonal tension, diagonal compression, and sliding shear (Paulay and Priestley 1992; Terzioglu et al. 2018). The type or combination of failure will depend on the design parameters such as horizontal and vertical web reinforcement ratio, wall geometry, and axial force level (Epackachi et al. 2018). In general, reinforced concrete structures subjected to earthquakes always tend to crack even if these structures are in a low to moderate seismic region; squat walls are not the exception. A reduction factor is usually applied to the stiffness to account for the effect of cracking in linear analysis. Design codes and seismic standards (e.g., FEMA, ASCE, and ACI) provide factors to reduce stiffness to account for the effects of cracking in the analyses and design. However, the basis for these stiffness reduction factors or stiffness expressions is not clearly presented in these standards and their applicability to nuclear plant elements could not be assessed (NUREG/CR 6926). The ASCE Standard 4-98 indicates that care should be exercised in modeling the stiffness of reinforced concrete elements depending on the level of stress and critical seismic load combinations in safety-related nuclear structures. Assumptions in stiffness can have a profound effect in the frequency of the system, could affect greatly the design seismic loads, and has an impact in the evaluation of RC elements or walls in NPPs for different performance objectives. The Nuclear Energy Agency (NEA) Committee on the Safety of Nuclear Installations (CSNI) has pointed out (NEA-CSNI 2003) that for the evaluation of NPPs at different performance limit states, a better understanding and prediction of the actual structural response is needed. In this regard, it is important to have a robust modeling scheme capable to capture initial stiffness and its changes as cracking occurs in the element in special for squat RC walls. Prediction of the seismic response and proper capturing of the effective stiffness for squat walls are a challenging task, since these walls exhibit a shear-dominated behavior with strong coupling between shear and flexure responses. In addition, this type of wall can present significant shear sliding, as cycles of inelastic excursions occur. While significant research has been performed during the past years to address this situation (Epackachi et al. 2015; Terzioglu et al. 2018; Ma and Li 2019), more research is still necessary to improve current modeling approaches for the seismic analysis of squat RC walls that can be used in the design office environment. Estimation of the lateral stiffness of structural members especially for squat RC walls is not something straightforward. Effective lateral stiffness of squat RC walls depends on multiple factors such as: (a) geometrical effect, (b) the intensity of axial loads, (c) the deterioration in stiffness, (d) the use of special details, (e) the modulus of elasticity of the concrete, and (f) reinforcement steel yield strength. Furthermore, a higher axial load can reduce the crack formed by tensile stress in concrete increasing the stiffness in the walls. The degradation of the flexural stiffness and shear stiffness is different and could be affected by the bond-slip deformation and slipping resistance between the wall and the foundation.

In this paper, the effective stiffness of RC squat walls and factors that affect its prediction are evaluated using a nonlinear finite model developed in ABAQUS. Seven RC shear wall specimens are modeled. The selected specimens were tested at the NEES facility at the University of New York at Buffalo (Rocks 2012; Luna et al. 2013). Current expressions for the calculation of lateral stiffness are evaluated and results are compared from the analytical model results. A parametric study is performed varying several concrete parameters to determine their impact in the lateral stiffness prediction.

Current expressions for lateral stiffness

Typically, the seismic design of RC structural members uses the results obtained from linear analyses in which appropriate modifications of the lateral stiffness of members are required. The theoretical initial in-plane lateral stiffness, K_t, is calculated, as shown in Eqs. (1–3). These equations are based on mechanics of materials theory:

$$K_{\text{t}} = \frac{1}{{\frac{1}{{K_{\text{f}} }} + \frac{1}{{K_{\text{s}} }}}},$$

(1)

$$K_{\text{s}} = \frac{{G_{\text{c}} A_{\text{g}} }}{{h_{\text{w}} }},$$

(2)

$$K_{\text{f}} = \frac{{3E_{\text{c}} I_{\text{g}} }}{{h_{\text{w}}^{3} }}.$$

(3)

In these equations K_s and K_f are shear and flexural rigidities, respectively, where $G_{\text{c}} = \frac{{E_{\text{c}} }}{{2\left( {1 + \upsilon } \right)}}$ is the shear modulus of concrete, E_c is the modulus of elasticity of concrete, I_g is the gross moment of inertia of the wall, A_g is the cross-sectional area of the wall, h_w is the height of the wall from the top of the foundation to the centerline of loading, and $\upsilon$ is the Poisson’s ratio. E_cI_g and G_cA_g are the flexural and shear stiffness, respectively.

For the calculation of the lateral effective stiffness of squat walls for linear analyses, some factors are used in building codes and standards of practice to reduce the initial theoretical lateral stiffness of the RC members. Reduction factors for the flexural and shear rigidities vary for uncracked and cracked reinforced concrete shear walls. For the calculation of effective moment of inertia (I_e), the ACI 318-14 (2014) recommend factors of 0.7 I_g and 0.35 I_g for an uncracked and cracked condition, respectively. ASCE 43-05 (2005) recommends no reduction in the flexural and shear rigidities for uncracked walls and a 50% reduction in both the flexural and shear rigidities for cracked walls. ASCE 41-13 (2013) recommends a reduction of 50% in the flexural rigidity but no reduction in the shear rigidity for cracked walls. Luna (2015) proposed reduction factors for the flexural and shear rigidity of low aspect ratio RC walls of 0.5EI_g and 0.35GA_g, respectively. FEMA 356 (2000) recommends a factor of 0.5EI_g and 0.4GA_g for flexural and shear rigidities, respectively. Li and Xiang (2011) proposed and equation to calculate the effective stiffness of squat RC walls accounting for deformations attributable to both flexural and shear actions (Eq. 4):

$$\frac{{I_{\text{e}} }}{{I_{\text{g}} }} = 0.19\left( {\frac{100}{{f_{\text{y}} }} + \frac{N}{{f_{\text{c}}^{{\prime }} A_{\text{g}} }}} \right)\left( {0.53 + 0.37\frac{{h_{\text{w}} }}{{L_{\text{w}} }} + 0.31\frac{{h_{\text{w}}^{2} }}{{L_{\text{w}}^{2} }}} \right) ,$$

(4)

where N = axial loads, f_y = yield strength of reinforcement, $f_{\text{c}}^{{\prime }}$ =compressive strength of concrete, A_g = gross area of wall’s section, h_w = height of cantilever wall, L_w = length of cantilever wall, I_g = gross moment of inertia, and I_e = effective moment of inertia.

Selected wall specimens for validation

Seven RC squat walls with four different aspect ratios were selected to develop the finite-element models. These walls correspond to phase I specimens of 12 RC shear walls with low aspect ratio built and tested at NEES facility at University of Buffalo (Rocks 2012). The thickness and length of the test specimens were 203 mm and 3048 mm, respectively. The walls are identified as SW1 to SW7 according to their aspect ratio (h_w/l_w) and vertical/horizontal reinforcing steel quantities (ρ_v and ρ_h). The concrete compressive ($f_{\text{c}}^{{\prime }}$), steel yield (f_y), and ultimate (f_u) strengths are shown in Table 1 and were obtained from Rocks (2012) and Luna (2015). Additional information is provided in these references.

Table 1 Properties of material of wall

Analytical modeling

Modeling scheme

Finite-element models of the seven selected RC squat walls were developed using the commercial software Abaqus (2016). The main objective of the finite-element models of these RC squat walls is to predict the lateral stiffness using the tools available in Abaqus and compare their results with the experimental tests available in literature. The walls were modeled using brick elements with 8 nodes linear reduce integrated hexagonal elements (C3D8R) and a mesh of 50 × 50 × 50 mm to represent the concrete. The reinforcement of the wall was modeled using 2-node linear truss elements (T3D2). To connect the concrete to the steel reinforcement, an embedded constrain type was used. A constrain type “tie” was used to connect the wall with the basement. This constrain connects two or more parts into the model no matter the type of mesh used on each part (wall or basement, Fig. 1).

Fig. 1

a Reinforcement of the wall with truss elements. b Wall with bricks elements and steel reinforcement embedded into the wall

Constitutive models

In the last decades, many constitutive models have been developed for the prediction of the concrete behavior. There are three models available in Abaqus to predict the behavior of the concrete: the smeared crack concrete model, concrete damage plasticity (CDP), and the brittle crack concrete model. The CDP model was selected for the concrete in the walls due to its higher potential of convergence compared with smeared crack approach and has the potential to represent the complete behavior of the concrete in the inelastic range for both tension and compression including damage characteristics. The CDP model requires the definition of the following parameters: uniaxial compression response, uniaxial tension response, ratio of initial equibiaxial compressive yield stress to initial uniaxial compressive yield stress (σ_b0/σ_c0), ratio of tension meridian and compression meridian deviator second stress invariants (Kc), eccentricity (e), and the dilation angle for the flow potential ($\psi$).

The uniaxial compressive response for unconfined concrete in the absence of reported data is represented using the numerical model of Popovics (1973) using the following equation:

$$f_{\text{c}} = f_{\text{c}}^{{\prime }} \frac{{r\left( {\frac{{\varepsilon_{\text{c}} }}{{\varepsilon_{{{\text{c}}0}} }}} \right)}}{{r - 1 + \left( {\frac{{\varepsilon_{\text{c}} }}{{\varepsilon_{{{\text{c}}0}} }}} \right)^{r} }},$$

(5)

$$r = \frac{{E_{\text{c}} }}{{E_{\text{c}} - E_{ \sec } }} ,$$

(6)

$$E_{ \sec } = \frac{{f_{\text{c}}^{{\prime }} }}{{\varepsilon_{{{\text{c}}0}} }} ,$$

(7)

where $f_{\text{c}}^{{\prime }}$ is the compressive strength, ε_c0 is the strain corresponding to $f_{\text{c}}^{{\prime }}$ the concrete compressive strength, and E_c is the modulus of elasticity of the concrete.

To define the compression compressive stress–strain relationship of for concrete in Abaqus, it is necessary to calculate inelastic strains ($\varepsilon_{\text{c}}^{{ \sim {\text{in}}}}$) corresponding to stress and damage values. The total strain is related to inelastic strains using Eq. (8):

$$\varepsilon_{\text{c}}^{{\sim {\text{in}}}} = \varepsilon_{\text{c}} - \varepsilon_{\text{oc}}^{\text{el}} ,$$

(8)

$$\varepsilon_{\text{oc}}^{\text{el}} = \frac{{\sigma_{\text{c}} }}{{E_{\text{o}} }},$$

(9)

where $\varepsilon_{\text{oc}}^{\text{el}}$ is the elastic strain that corresponds to the undamaged material and ε_c is the total compressive strain. Special care must be taken with negative plastic strain compressive values $\varepsilon_{\text{c}}^{{\sim {\text{pl}}}}$, because they are indicative of incorrect damage curves which may lead to generate error massage before the analysis is performed. The plastic strain is defined by the following equation:

$$\varepsilon_{\text{c}}^{{\sim {\text{pl}}}} = \varepsilon_{\text{c}}^{{\sim {\text{in}}}} - \frac{{d_{\text{c}} }}{{\left( {1 - d_{\text{c}} } \right)}}\frac{{\sigma_{\text{c}} }}{{E_{\text{o}} }}.$$

(10)

Figure 2 shows the typical compressive stress–strain relationship with damage properties and the calculated curves for the seven selected specimens.

Fig. 2

a Compressive stress–strain relationship (Abaqus manual-2016), b compressive concrete stress–strain curves for selected specimens

To describe the stress–strain relationship for concrete in tension, the model of Belarbi and Hsu (1994) was used. Eqs. (11) and (12) define this constitutive model:

$$\sigma_{\text{t}} = E_{\text{c}} \varepsilon_{\text{t}} \quad \varepsilon_{\text{t}} \le \varepsilon_{\text{cr}} ,$$

(11)

$$\sigma_{\text{t}} = f_{\text{t}} \left( {\frac{{\varepsilon_{\text{cr}} }}{{\varepsilon_{t} }}} \right)^{0.4} \quad \varepsilon_{\text{t}} > \varepsilon_{\text{cr}} ,$$

(12)

where E_c is the modulus of elasticity, f_t is the direct tensile strength of concrete, and $\varepsilon_{\text{cr}}$ is the strain associate to critic tension stress. To develop this model in Abaqus, it is required the modulus of elasticity (E_c), the tensile stress (σ_t), the cracking strain values ($\varepsilon_{\text{t}}^{{\sim {\text{ck}}}} = \varepsilon_{\text{t}} - \varepsilon_{\text{ot}}^{\text{el}} )$, and the damage parameter (d_t), where $\varepsilon_{\text{ot}}^{\text{el}} = \frac{{\sigma_{\text{t}} }}{{E_{\text{o}} }}$ is the elastic strain corresponding to the undamaged material and $\varepsilon_{\text{t}}$ is the total tensile strain. Special care must be taken to ensure that the plastic tensile strain values $\varepsilon_{\text{t}}^{{\sim {\text{pl}}}} = \varepsilon_{\text{t}}^{{\sim {\text{in}}}} - \frac{{d_{\text{t}} }}{{\left( {1 - d_{\text{t}} } \right)}}\frac{{\sigma_{\text{t}} }}{{E_{\text{o}} }}$ are not negative or decreasing. Figure 3 shows a typical tensile stress–strain relationship with damage properties and the calculated curves for the selected specimens.

Fig. 3

a Tensile stress–strain relationship (Abaqus manual), b tensile concrete stress–strain (Chang and Mander 1994)

The parameters required to define the yield function for the CDP model are: the compressive yield stress ratio (σ_b0/σ_c0) for concrete, the parameter Kc and the dilation angle. The influence of these parameters in the wall stiffness and lateral response was evaluated by means of a parametric study.

The wall reinforcement is modeled as an elasto-plastic material with isotropic hardening, based on the constitutive model proposed by Chang and Mander (1994). In this model the steel behavior is divided in three parts: the elastic branch $0 \le \varepsilon_{\text{s}} \le \varepsilon_{\text{y}}$

$$f_{\text{s}} = E_{\text{s}} \varepsilon_{\text{s}} ,\quad E_{\text{t}} = E_{\text{s}} ,$$

(13)

where $\varepsilon_{\text{y}} = f_{\text{y}} /E_{\text{s}}$, $\varepsilon_{\text{y}} = {\text{yield strain}}$, $f_{\text{y}} = {\text{yield stress}}$, $E_{\text{s}} = {\text{Elastic Modulus of Elasticity}} .$

The Yield Plateau $\varepsilon_{\text{y}} < \varepsilon_{\text{s}} < \varepsilon_{\text{sh}}$, where $f_{\text{s}} = f_{\text{y}}$, $E_{\text{t}} = 0$, in which $\varepsilon_{\text{sh}} = {\text{strain hardening}}.$

The Strain Hardening Branch $\varepsilon_{\text{s}} \ge \varepsilon_{\text{sh}}$

$$f_{\text{s}} = f_{\text{su}} + \left( {f_{\text{y}} - f_{\text{su}} } \right)\left| {\frac{{\varepsilon_{\text{su}} - \varepsilon_{\text{s}} }}{{\varepsilon_{\text{su}} - \varepsilon_{\text{sh}} }}} \right|^{P} ,\quad P = E_{\text{sh}} \frac{{\varepsilon_{\text{su}} - \varepsilon_{\text{sh}} }}{{f_{\text{su}} - f_{\text{y}} }},$$

(14)

where $\varepsilon_{\text{su}} =$ is the stress at ultimate stress, $f_{\text{su}} =$ ultimate (maximum) stress.

The two reinforcement parameters that should be inserted into Abaqus are: true stress $f_{\text{tru}} = f_{\text{s}} \left( {1 + \varepsilon_{\text{s}} } \right)$ and plastic strain $\varepsilon_{\text{pl}} = \varepsilon_{\text{true}} - f_{\text{true}} /E_{\text{s}}$, where $\varepsilon_{\text{true}} = { \ln }\left( {1 + \varepsilon_{\text{s}} } \right)$ is defined as true strain of the material.

Modeling results and discussion

Parametric study of K _c and σ _b0/σ _c0

According to Lubliner et al. (1989), the parameters K_c and σ_b0/σ_c0 can take values of 0.67 and 1.16, respectively. A parametric study of how these parameters affect the behavior of squat wall models in a pushover analysis was performed in Abaqus. For the K_c parameter, two extreme values of 0.5 and 1.0 were considered to analyze the wall models. The analyses were also performed varying the parameter σ_b0/σ_c0 with values 1.1 and 1.16 (Fig. 4). The models used in this analysis were the walls SW1 and SW7 with aspect ratios of 0.94 and 0.33, respectively. Minimal changes in the wall response were obtained with the variation of these parameters, as shown in Fig. 4.

Fig. 4

Variation of parameters K_c and σ_b0/σ_c0, for walls SW1 and SW7

Parametric study-dilation angle

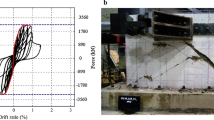
For all seven squat walls, it was necessary to determine an appropriate dilation angle ($\psi$). For this purpose, a parametric analysis was conducted for all wall models varying the dilation angles from 35° to 56°. The models were subjected to lateral loads (pushover). Figure 5 shows how dilation angle affects the shear wall vs drift response for walls SW1–SW7 for three dilation angle cases (35°, 45°, and 56°). As shown in this figure, as the dilation angle increases, the results improve when compared with the experimental test values. From these analyses, it was determined that the dilation angle that better predicts the lateral response of these squat walls is 56°.

Fig. 5

Pushover analysis of shear walls for different dilation angles

Parametric study on ultimate concrete strain

Once the appropriate dilation angle was found for the analyses, additional calibrations were performed. Two tests were performed in which the concrete compressive constitutive curve was varied. The first analyses were performed with a variation of the Popovics (1973) curve that is more typical of an unconfined concrete. In this curve, when the concrete reaches a strain of 0.004, the strength begins to drop lineally until a strain of 0.0064. The second analyses were performed with the whole compressive concrete curve obtained from the Popovics Eq. (5). These two curves are shown in Fig. 6.

Fig. 6

Compressive concrete curves used in the analyses

Figure 7 shows the results of the analytical model in Abaqus (shear vs drift) and the average backbone curve from the experimental tests (Rocks 2012) using the first and third quadrants of loading curves. As seen in these figures, the best results are obtained using the Popovics curve until a concrete deformation of 0.01. This concrete curve allows a better estimation of the peak and post peak response of these walls. Nevertheless, using a concrete curve with a drop of strength until a strain of 0.0064, we can give a good estimation of shear peak and its, respectively, strain, but the post peak response is not predicted well (Fig. 7).

Fig. 7

Base shear vs drift for different concrete models

Lateral stiffness calculation

The effective stiffness of experimental walls was compared with different stiffnesses calculated by codes using reduction flexural and shear factors (Table 2). The experimental effective stiffness data were obtained from Luna (2015). From Table 2, it can be noticed that the reduction factors that provide a better approximation of the effective stiffness are the factors proposed by Luna and ASCE 43-05 for cracked walls. The other factors provided in the ASCE 43-05 for uncracked walls, ASCE 41-13 for cracked walls, ACI 318-14, and FEMA 356 standards overestimate the results. The effective stiffness was also calculated for the calibrated 3D model using the software Abaqus (2016). It was obtained at 15% of the shear peak and its, respectively, displacement as recommended by Luna (2015). Figure 8 presents the error percentages of all the different effective stiffness calculations in relation with the experimental data. Error percentages varied from 5.7 to 22.5% for the finite-element model developed in Abaqus. The analytical model predicts with good approximation the effective stiffness taking into consideration that the wall response at low levels of drifts presents more variability. Theoretical stiffness (K_t) values were calculated using the formulas derived from mechanics of materials (Eqs. 1–3).

Table 2 Effective stiffness wall values

Fig. 8

Error percentages of effective stiffness calculation compared with experimental data

Conclusions

This paper presented a study of the effective lateral stiffness of RC squat walls. Finite-element models of seven walls were developed to determine which modeling parameters provide the best agreement in lateral stiffness and peak strength. In Abaqus, the Concrete Damage Plasticity Model was evaluated by means of a parametric study focusing on important concrete parameters. From these analyses, it was determined,

• The parameter that has more influence in the response of the walls analyzed in this study was the dilation angle of the concrete. An angle of 56° better captures the response of these walls and provides accurate results of lateral stiffness and peak shear values.

• The prediction of the lateral response of the walls analyzed in this research was better obtained with the constitutive relationship of the concrete based on the Popovics curve. Additional studies are recommended to improve the post peak response of the squat walls with other constitutive models.

• The parameters K_c and σ_b0/σ_c0 have a minimal impact in the wall response and lateral stiffness.

From the evaluation of existing lateral stiffness factors and equations, it was assessed that the reduction factors that provide a better approximation of the effective stiffness are the factors proposed by Luna and ASCE 43-05 for cracked walls. The finite-element models developed in Abaqus provide results that are in good agreement with the experimental data.