Introduction

Polyolefins, the largest group of thermoplastics, are recognized to be cost-effective and showing excellent characteristics in a remarkable wealth of applications mainly as packaging, machinery parts, medical applications and domestic appliances. Covering 60% of the total polyolefin production, polyethylene is considered as the dominant polymer applied in the industry. Polyethylene is practically obtained in many types of reactor configurations ranging from autoclaves and loop reactors, to fluidized bed reactors. Owing to operation at lower temperatures and pressures, no need for solvent, and better heat removal, gas-phase polymerization of ethylene in catalytic fluidized bed reactors is proved to be favorable for producing a broad range of polyethylene grades [1,2,3].

Various mathematical models have been proposed by researchers to characterize the performance of gas-phase ethylene polymerization reactors. Modeling these reactors began with the pioneering work of Choi and Ray [4], who considered both emulsion and bubble phases in modeling a polyethylene fluidized bed reactor assuming constant bubble size along the bed. Several authors proposed a well-mixed model by considering the polymerization reaction occurring in a CSTR. They indicated that the simplifications are reasonable since virtually no loss of phenomenological information is observed [5,6,7,8,9,10,11]. Fernandes and Lona [12] presented a three-phase model which is comprised of emulsion gas, polymer particles and bubble. Hatzantonis et al. [13] divided the reactor into two sections: an emulsion phase, which is perfectly agitated and a bubble phase, which is divided into N well-mixed compartments in series. They developed a model to account for the effects of varying bubble size with respect to the bed height on the reactor dynamics and product properties. A pseudo-homogenous model was proposed by Alizadeh et al. [2] assuming an average concentration of particles in the bed. They employed a tanks-in-series model to characterize the flow pattern in the reactor. In fluidized bed polymerization reactors, the challenges of design and control are related to achieving adequate heat removal and production rate [14,15,16]. Also, other approaches were explored which dealt with grade transition, molecular weight and density control of the polymer [17,18,19,20].

The process studied in the present work is the new Spherilene technology licensed by LyondellBasell which includes two gas-phase reactors in series for polyethylene production. This process is designed for the production of the entire density range of polyethylene products, from linear low density polyethylene (LLDPE), to medium density polyethylene (MDPE) and high density polyethylene (HDPE). Due to the fact that many of the end-use properties of the produced polymer depend on the reaction conditions that are usually difficult to be measured online, there is a need to simulate the process to obtain an optimal estimation of the process parameters. The dynamic simulation of industrial polymerization reactor series for fluidized bed reactors are currently lacking in literature. A well-mixed model is adopted in unsteady-state conditions to simulate the dynamic behavior of the LLDPE production process. The model is developed with flexibility to be applied for the entire range of LLDPE by modifying the input values and initial conditions. Also, it is capable of predicting the crucial properties of the polymer in the reactors and the characteristics of the final product. The effects of catalyst flow rate, monomer concentration and distribution of catalyst active sites on the polymer properties and reactor behavior are also examined. Then, by modifying the model, a conventional feedback control system is applied to maintain the temperature and the height of each reactor at desired values, and the operability of the plant’s control system in the presence of common disturbances is evaluated.

Reactor modeling

Series reactor process

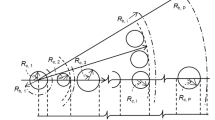
In Fig. 1, a schematic representation of the industrial polymerization reactors considered in this study is depicted. Heterogeneous Ziegler–Natta catalyst for this process is composed of TiCl4 supported on MgCl2 crystal, and AlEt3 is added as co-catalysts. The catalyst is activated in a pre-contact vessel, and fed into two prepolymerization loop reactors in series to be capsulated with propylene before entering the fluidized bed reactors. The prepolymerization prevents the possible difficulties that can arise at the demanding conditions of the main polymerization reactors with fresh catalyst. This step is like polymerization but under milder conditions compared to the main polymerization process, in which small-sized prepolymer particles are formed [21, 22]. Directly after the reactive species reach an active site, the polymer layer is formed over the active site, inside the porous space of the supported catalyst. By accumulation of polymer at the active sites, the inorganic phase suffers a local build-up of stress that causes weak points of the solid structure to break, and the support starts to fragment into a series of unconnected mineral substructures maintained by a polymer phase [23]. The prepolymerization step gives a prepolymer particle the ability to mechanically withstand, or decreases the reaction peak by generating an amount of stress sufficient for the particles to fragment, but not so much and not too quickly that they be disintegrated [24]. Therefore, the prepolymerization step can have a significant effect on the fragmentation behavior of the catalyst particles, and it also reduces the risk of particle overheating [22].

Fig. 1
figure 1

SPHERILENE process

Full size image

The feed of fluidized bed polymerization reactors includes a mixture of ethylene, 1-butene as co-monomer, hydrogen and the activated catalyst. Due to low single-pass conversion (3–5%), large recycle stream is provided to restore unreacted feed. The stream of unreacted gases which exits from the top of the reactor also removes the reaction heat by passing through a heat exchanger in a counter-current flow with cooling water. The second reactor utilizes independent feed streams of ethylene, 1-butene and hydrogen. The active catalyst from the first reactor is fed together with the product of the first reactor to the second one to continue the reaction at the same or different conditions. About 70–85% of the polymerization occurs in the second reactor, depending on the required properties of the effluent.

Kinetics

Since industrial production of polyethylene includes copolymerization processes, it is of essential importance to perceive kinetic behavior and polymer properties via investigating the copolymerization mechanism. For Ziegler–Natta catalyst as a multi-site-type catalyst, it is generally assumed that two or more active sites are present, each with its own characteristics and kinetic rate constants. This leads to producing polymer chains with distinct properties [25].

In the present study, a comprehensive mechanism is undertaken to characterize the copolymerization kinetics of ethylene and 1-butene in both reactors, with two different active sites based on the kinetic model proposed by Dompazis et al. [26]. As tabulated in Table 1, the kinetic comprises the key elementary reactions, including site activation, propagation, site deactivation and site transfer reactions. The kinetic rate constants in each active site are expressed as pseudo-kinetic rate constants for further simplification, as summarized in Table 2. Site activation, deactivation and chain transfer reactions are governed by the following functions for catalyst sites of type “k”:

Table 1 Kinetic mechanism of ethylene copolymerization over a Ziegler–Natta catalyst [22]
Full size table
Table 2 Pseudo-kinetic rate constants [22]
Full size table

Potential sites:

$$R_{\text{sp}}^{k} = - K_{aA}^{k} \left[ A \right]\left[ {S_{p}^{k} } \right].$$
(1)

Vacant sites:

$$R_{{{\text{P}}0}}^{\text{k}} = - K_{dsp}^{k} \left[ {P_{0}^{k} } \right] - \mathop \sum \limits_{i = 1}^{{N_{m} }} K_{0,i}^{k} \left[ {P_{0}^{k} } \right]\left[ {M_{i} } \right] - R_{sp}^{k} + K_{tH,T}^{k} \left[ {H_{2} } \right]\lambda_{0}^{k} .$$
(2)

Pseudo-kinetic rate constant for chain transfer reactions:

$$r_{{{\text{t}},{\text{T}}}}^{\text{k}} = K_{tH,T}^{k} \left[ {H_{2} } \right].$$
(3)

All symbols appearing in the above equations are explained in the nomenclature section.

Once the “live” and “bulk” moments are defined according to the postulated mechanism, the total consumption rate of the “i” monomer will be given by

$$R_{\text{Mi}}^{k} = \left[ {M_{i} } \right]\mathop \sum \limits_{k = 1}^{2} \left[ {K_{0,i}^{k} \left[ {P_{0}^{k} } \right] + K_{p,Ti}^{k} \lambda_{0}^{k} } \right].$$
(4)

Mass and energy balances

The assumptions made in developing the equations of the model are summarized as below:

  • Due to the large recycle stream to fresh feed ratio, which is almost 40 in this study, the fluidized bed is approximated by a CSTR, consisting of well-mixed solid and gas phases in contact with each other.

  • Temperature gradient and radial concentration gradient in the reactors are neglected.

  • Mass and heat transfer resistance between the emulsion phase and the solid particles are considered to be insignificant.

  • A mean size is assumed for the polymer particles, and elutriation of solid particles at the top of the bed is assumed to be negligible.

  • The product removal rates from the reactors are considered such that the bed is maintained at a constant level.

  • In the model proposed in this section, the temperature of the recycled gas is assumed constant, and the heat exchanger dynamics is excluded from the balance equations.

Based on the above assumptions, the unsteady-state material and energy conservation equations of the first reactor are derived by following the procedure developed by Hatzantonis et al. [13].

To predict the compositions of monomer “i” and hydrogen in the reactor at any time:

$$\frac{{{\text{d}}\left[ {M_{i,1} } \right]}}{{{\text{d}}t}} = \frac{{(M_{i,1} )_{\text{in}} }}{{A_{1} H_{1} \varepsilon_{1} }} - \frac{{\left( {1 - \varepsilon_{1} } \right)A_{1} H_{1} \varepsilon_{1} R_{{M_{i,1} }} }}{{A_{1} H_{1} \varepsilon_{1} }},$$
(5)

where index “1” represents the properties of the first reactor and ε accounts for the overall gas volume fraction in the bed. The dynamic mass balance for the catalyst is given by

$$\frac{{{\text{d}}C_{{{\text{cat}},1}} }}{{{\text{d}}t}} = \frac{{f_{\text{cat}} }}{{A_{1} H_{1} \left( {1 - \varepsilon_{1} } \right)\rho_{{{\text{cat}},1}} }} - \frac{{q_{1} C_{{{\text{cat}},1}} }}{{A_{1} H_{1} \left( {1 - \varepsilon_{1} } \right)}}.$$
(6)

In Eq. 6, q1 and fcat are the rate of product removal and the fresh catalyst, respectively. Mass balance for the “k-type” potential active site can be written as

$$\frac{{{\text{d}}S_{p,1}^{k} }}{{{\text{d}}t}} = \frac{{f_{\text{cat}} S_{{p,1,{\text{in}}}}^{k} }}{{A_{1} H_{1} \left( {1 - \varepsilon_{1} } \right)}} - R_{{{\text{sp}},1}}^{k} - \frac{{q_{1} S_{p,1}^{k} }}{{A_{1} H_{1} \left( {1 - \varepsilon_{1} } \right)}},$$
(7)

where \(S_{{p,1,{\text{in}}}}^{k} = \left[ {Me} \right]A_{\text{sf}}^{k}\). Similarly, the following balances are applied for the live and bulk copolymer chains of length “n”.

$$\frac{{{\text{d}}X_{1}^{k} }}{{{\text{d}}t}} = R_{X,1}^{k} - \frac{{q_{1} X_{1}^{k} }}{{A_{1} H_{1} \left( {1 - \varepsilon_{1} } \right)}}.$$
(8)

The rate of the withdrawn product is given by

$$q_{1} = \frac{{A_{1} H_{1} \left( {1 - \varepsilon_{1} } \right)\mathop \sum \nolimits_{i = 1}^{{N_{m} }} MW_{i} \left[ {M_{i,1} } \right]}}{{\left( {1 - \varepsilon_{1} } \right)\rho_{{{\text{poly}},1}} + \varepsilon_{1} \mathop \sum \nolimits_{i = 1}^{{N_{m} }} MW_{i} \left[ {M_{i,1} } \right]}},$$
(9)

which is equal to the rate of polymer production. All these mass conservation equations are valid for the second reactor too, except for the potential active site and catalyst mass balances. Due to the fact that there is no fresh catalyst feed, and the only catalyst supply is the product stream leaving the first reactor, these mass balances are modified as below:

$$\frac{{{\text{d}}C_{{{\text{cat}},2}} }}{{{\text{d}}t}} = \frac{{q_{1} C_{{{\text{cat}},1}} }}{{A_{2} H_{2} \left( {1 - \varepsilon_{2} } \right)}} - \frac{{q_{2} C_{{{\text{cat}},2}} }}{{A_{2} H_{2} \left( {1 - \varepsilon_{2} } \right)}},$$
(10)
$$\frac{{{\text{d}}S_{p,2}^{k} }}{{{\text{d}}t}} = \frac{{q_{1} S_{p,1}^{k} }}{{A_{2} H_{2} \left( {1 - \varepsilon_{2} } \right)}} - \frac{{q_{2} S_{p,2}^{k} }}{{A_{2} H_{2} \left( {1 - \varepsilon_{2} } \right)}}.$$
(11)

The overall dynamic energy balance for the first reactor can be expressed as

$$\begin{aligned} & \left[ {\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,1} } \right]C_{{PM_{i} }} + \frac{{1 - \varepsilon_{1} }}{{\varepsilon_{1} }} \rho_{\text{poly}} C_{{P,{\text{poly}}}} } \right]\frac{{{\text{d}}T_{1} }}{{{\text{d}}t}} \\ & \quad = \mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,1} } \right]_{\text{in}} C_{{PM_{i} }} \left( {T_{{{\text{in}},1}} - T_{\text{ref}} } \right) - \left( {\frac{{q_{1} }}{{A_{1} H_{1} \varepsilon_{1} }}} \right)\left( {\rho_{\text{poly}} C_{{P,{\text{poly}}}} } \right)\left( {T_{1} - T_{\text{ref}} } \right) \\ & \quad - \left( {\frac{{u_{0,1} }}{{H_{1} \varepsilon_{1} }}} \right)\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,1} } \right]C_{{PM_{i} }} \left( {T_{1} - T_{\text{ref}} } \right) + \left( {\frac{{u_{0,1} }}{{H_{1} \varepsilon_{1} }}} \right)\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,1} } \right]C_{{PM_{i} }} \left( {T_{{{\text{rec}},1}} - T_{\text{ref}} } \right) \\ & \quad + \frac{{1 - \varepsilon_{1} }}{{\varepsilon_{1} }}\mathop \sum \limits_{i = 1}^{{N_{m} }} \Delta H_{{rxn_{i} }} R_{{M_{i} ,1}} , \\ \end{aligned}$$
(12)

where u0 is the superficial gas velocity of the recycle stream. For the second reactor we have:

$$\begin{aligned} & \left[ {\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,2} } \right]C_{{PM_{i} }} + \frac{{1 - \varepsilon_{2} }}{{\varepsilon_{2} }} \rho_{\text{poly}} C_{{P,{\text{poly}}}} } \right]\frac{{{\text{d}}T_{2} }}{{{\text{d}}t}} \\ & \quad = \mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,2} } \right]_{\text{in}} C_{{PM_{i} }} \left( {T_{{{\text{in}},2}} - T_{\text{ref}} } \right) + \left( {\frac{{q_{1} }}{{A_{2} H_{2} \varepsilon_{2} }}} \right)\left( {\rho_{\text{poly}} C_{{P,{\text{poly}}}} } \right)\left( {T_{1} - T_{\text{ref}} } \right) \\ & \quad - \left( {\frac{{q_{2} }}{{A_{2} H_{2} \varepsilon_{2} }}} \right)\left( {\rho_{\text{poly}} C_{{P,{\text{poly}}}} } \right)\left( {T_{2} - T_{\text{ref}} } \right) - \left( {\frac{{u_{0,2} }}{{H_{2} \varepsilon_{2} }}} \right)\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,2} } \right]C_{{PM_{i} }} \left( {T_{2} - T_{\text{ref}} } \right) \\ & \quad + \left( {\frac{{u_{0,2} }}{{H_{2} \varepsilon_{2} }}} \right)\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,2} } \right]C_{{PM_{i} }} \left( {T_{{{\text{rec}},2}} - T_{ref} } \right) + \frac{{1 - \varepsilon_{2} }}{{\varepsilon_{2} }}\mathop \sum \limits_{i = 1}^{{N_{m} }} \Delta H_{{rxn_{i} }} R_{{M_{i} ,2}} . \\ \end{aligned}$$
(13)

All initial conditions for governing equations are given in Table 3.

Table 3 Initial conditions of the reactors
Full size table

Reactor control system with modified model

In this section, we assess the closed-loop performance of the process in load rejection under a conventional feedback PID algorithm. Since there is a critical bed level, below which a relatively rapid polymer wash out occurs, adequate bed level control is demanded in the ethylene polymerization fluidized bed reactors. Tight temperature control is also crucial for keeping the reaction zone temperature at its desired value to prevent particle agglomeration. To implement a control structure that controls the height and temperature of each reactor, the assumptions and consequently the equations of the mathematical model proposed in the previous section require modifications.

To adjust the model, the height of the beds is assumed to be variable and the dynamics of two external shell-and-tube heat exchangers, which transfer the heat of reaction by recirculating the unreacted gases in counter-current flow with cooling water, are taken into considerations. As a result, Eqs. (5–8) are modified to the following equations:

$$\frac{{{\text{d}}\left( {H_{1} \left[ {M_{i,1} } \right]} \right)}}{{{\text{d}}t}} = \frac{{(M_{i,1} )_{\text{in}} }}{{A_{1} \varepsilon_{1} }} - \frac{{\left( {1 - \varepsilon_{1} } \right)A_{1} H_{1} \varepsilon_{1} R_{{M_{i,1} }} }}{{A_{1} \varepsilon_{1} }},$$
(14)
$$\frac{{{\text{d}}(H_{1} C_{{{\text{cat}},1}} )}}{{{\text{d}}t}} = \frac{{f_{\text{cat}} }}{{A_{1} \left( {1 - \varepsilon_{1} } \right)\rho_{{{\text{cat}},1}} }} - \frac{{q_{1} C_{{{\text{cat}},1}} }}{{A_{1} \left( {1 - \varepsilon_{1} } \right)}},$$
(15)
$$\frac{{{\text{d}}(H_{1} S_{p,1}^{k} )}}{{{\text{d}}t}} = \frac{{f_{\text{cat}} S_{{p,1,{\text{in}}}}^{k} }}{{A_{1} \left( {1 - \varepsilon_{1} } \right)}} - H_{1} R_{{{\text{sp}},1}}^{k} - \frac{{q_{1} S_{p,1}^{k} }}{{A_{1} \left( {1 - \varepsilon_{1} } \right)}},$$
(16)
$$\frac{{{\text{d}}(H_{1} X_{1}^{k} )}}{{{\text{d}}t}} = H_{1} R_{X,1}^{k} - \frac{{q_{1} X_{1}^{k} }}{{A_{1} \left( {1 - \varepsilon_{1} } \right)}}.$$
(17)

In this case, the withdrawal rate of the product is not equal to the rate of polymer production.

Hence, Eqs. (10) and (11) are modified to the following equations:

$$\frac{{{\text{d}}(H_{2} C_{{{\text{cat}},2}} )}}{{{\text{d}}t}} = \frac{{q_{1} C_{{{\text{cat}},1}} }}{{A_{2} \left( {1 - \varepsilon_{2} } \right)}} - \frac{{q_{2} C_{{{\text{cat}},2}} }}{{A_{2} \left( {1 - \varepsilon_{2} } \right)}},$$
(18)
$$\frac{{{\text{d}}(H_{2} S_{p,2}^{k} )}}{{{\text{d}}t}} = \frac{{q_{1} S_{p,1}^{k} }}{{A_{2} \left( {1 - \varepsilon_{2} } \right)}} - \frac{{q_{2} S_{p,2}^{k} }}{{A_{2} \left( {1 - \varepsilon_{2} } \right)}}.$$
(19)

The energy balances of the first and the second reactors are also changed as follows:

$$\begin{aligned} & \left[ {\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,1} } \right]C_{{PM_{i} }} + \frac{{1 - \varepsilon_{1} }}{{\varepsilon_{1} }} \rho_{\text{poly}} C_{{P,{\text{poly}}}} } \right]\frac{{{\text{d}}(H_{1} T_{1} )}}{{{\text{d}}t}} \\ & = \mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,1} } \right]_{\text{in}} C_{{PM_{i} }} H_{1} \left( {T_{in,1} - T_{\text{ref}} } \right) - \left( {\frac{{q_{1} }}{{A_{1} \varepsilon_{1} }}} \right)\left( {\rho_{\text{poly}} C_{{P,{\text{poly}}}} } \right)\left( {T_{1} - T_{\text{ref}} } \right) \\ & - \left( {\frac{{u_{0,1} }}{{\varepsilon_{1} }}} \right)\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,1} } \right]C_{{PM_{i} }} \left( {T_{1} - T_{\text{ref}} } \right) + \left( {\frac{{u_{0,1} }}{{\varepsilon_{1} }}} \right)\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,1} } \right]C_{{PM_{i} }} \left( {T_{{{\text{rec}},1}} - T_{\text{ref}} } \right) \\ & + \frac{{1 - \varepsilon_{1} }}{{\varepsilon_{1} }}H_{1} \mathop \sum \limits_{i = 1}^{{N_{m} }} \Delta H_{{rxn_{i} }} R_{{M_{i} ,1}} , \\ \end{aligned}$$
(20)
$$\begin{aligned} & \left[ {\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,2} } \right]C_{{PM_{i} }} + \frac{{1 - \varepsilon_{2} }}{{\varepsilon_{2} }} \rho_{\text{poly}} C_{{P,{\text{poly}}}} } \right]\frac{{{\text{d}}(H_{2} T_{2} )}}{{{\text{d}}t}} \\ & \quad = \mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,2} } \right]_{\text{in}} C_{{PM_{i} }} H_{2} \left( {T_{{{\text{in}},2}} - T_{\text{ref}} } \right) + \left( {\frac{{q_{1} }}{{A_{2} \varepsilon_{2} }}} \right)\left( {\rho_{\text{poly}} C_{{P,{\text{poly}}}} } \right)\left( {T_{1} - T_{\text{ref}} } \right) \\ & \quad - \left( {\frac{{q_{2} }}{{A_{2} \varepsilon_{2} }}} \right)\left( {\rho_{\text{poly}} C_{{P,{\text{poly}}}} } \right)\left( {T_{2} - T_{\text{ref}} } \right) - \left( {\frac{{u_{0,2} }}{{\varepsilon_{2} }}} \right)\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,2} } \right]C_{{PM_{i} }} \left( {T_{2} - T_{\text{ref}} } \right) \\ & \quad + \left( {\frac{{u_{0,2} }}{{\varepsilon_{2} }}} \right)\mathop \sum \limits_{i = 1}^{{N_{m} }} \left[ {M_{i,2} } \right]C_{{PM_{i} }} \left( {T_{{{\text{rec}},2}} - T_{\text{ref}} } \right) + \frac{{1 - \varepsilon_{2} }}{{\varepsilon_{2} }}H_{2} \mathop \sum \limits_{i = 1}^{{N_{m} }} \Delta H_{{rxn_{i} }} R_{{M_{i} ,2}} . \\ \end{aligned}$$
(21)

The equations for the shell side and the tube side of the first heat exchanger are given by the following equations, respectively:

$$\frac{{{\text{d}}T_{w} }}{{{\text{d}}t}} = \frac{{F_{w} C_{Pw} \left( {T_{{w,{\text{in}}}} - T_{w} } \right) + U_{{{\text{ex}}1}} A_{{{\text{ex}}1}} \left( {T_{{{\text{rec}},1}} - T_{w} } \right)}}{{V_{{{\text{shell}}1}} \rho_{w} C_{Pw} }},$$
(22)
$$\frac{{{\text{d}}T_{{{\text{rec}},1}} }}{{{\text{d}}t}} = \frac{{u_{0,1} A_{1} \mathop \sum \nolimits_{i = 1}^{{N_{m} }} \left[ {M_{i,1} } \right]C_{{PM_{i} }} \left( {T_{1} - T_{{{\text{rec}},1}} } \right) - U_{{{\text{ex}}1}} A_{{{\text{ex}}1}} \left( {T_{{{\text{rec}},1}} - T_{w} } \right)}}{{V_{{{\text{tube}}1}} \mathop \sum \nolimits_{i = 1}^{{N_{m} }} \left[ {M_{i,1} } \right]C_{{PM_{i} }} }}.$$
(23)

The same equations are applied for the shell side and the tube side of the second heat exchanger.

The proposed control structure for industrial polyethylene reactors is depicted in Fig. 1. Based on the process experience, the cooling water flowrate of the heat exchangers is manipulated to control the bed temperature of each reactor and the polymer product is withdrawn from each reactor at a rate that controls the bed height.

Results and discussion

The performance of the reactors has been surveyed in two levels. In the first level, the model described in Sect. 2.3 is employed to specify the reactor behavior in addition to polymer properties, and the second level examines the performance of the proposed control structure by exerting the modified model presented in Sect. 3. The operating conditions and the model parameters are presented in Table 4, which are associated with the typical parameters of the industrial-scale polyethylene reactors for producing grade HD-52518.

Table 4 Operating conditions and numerical values of the physical and transport properties of the reaction mixture
Full size table

Open-loop simulation

To assess the results of the proposed model in Sect. 2.3 (with constant bed level and constant recycle temperature), the MFI of each product is compared to those of actual plant data, as shown in Fig. 2. The MFI is estimated using Eq. (24) suggested by McAuley et al. [5] in which constants are modified to fit the actual data presented in this study. As shown in Fig. 2, the results computed by the model and actual plant data are in good agreement.

$${\text{MFI}} = 2.128 \times 10^{17} \,{\text{MW}}^{ - 3.28} .$$
(24)

Furthermore, the comparison between the calculated MWD and GPC measurements is illustrated in Fig. 3. The marked points represent the results of the GPC measurements, and the solid line is the calculated MWD of the final product. Considering this comparison, it can be seen that there is good agreement between the two MWDs. These results reflect the validity of the model.

Fig. 2
figure 2

Actual and calculated MFI comparison

Full size image
Fig. 3
figure 3

GPC curve fit of LLDP for the final product

Full size image

Figure 4 clarifies the transient behavior of the reactors in terms of the variations in production rates of the polymer in both reactors. It is indicated that the production rates reach their steady-state values after about 20 h. These values are about 30 ton/h and 12 ton/h for the first and the second reactors, respectively, which are the same production rate applied in the industrial plant.

Fig. 4
figure 4

Evolution of the production rates of the two reactors over the residence time

Full size image

The polydispersity index, which indicates the width of the molecular weight distribution, is defined by [27]

$${\text{PDI}} = \frac{{\bar{M}_{w} }}{{\bar{M}_{n} }},$$
(25)

where

$$\bar{M}_{n} = \frac{{\xi_{1} }}{{\xi_{0} }}\sum\limits_{k = 1}^{{N_{s} }} {\overline{MW} } ,$$
(26)
$$\bar{M}_{w} = \frac{{\xi_{2} }}{{\xi_{1} }}\sum\limits_{k = 1}^{{N_{s} }} {\overline{MW} } ,$$
(27)
$$\overline{MW} = \sum\limits_{i = 1}^{{N_{m} }} {\varphi_{i}^{k} Mw_{i} } .$$
(28)

Figure 5 shows the evolution of the polydispersity indexes with respect to the time, which reach to a final value of 2.17 and 2.3 for the first and the second reactors, respectively. The molecular weight distributions for these PDIs are illustrated in Fig. 6. To stipulate the molecular weight distribution of the product, the two-parameter Schulz–Flory distribution is employed [28]:

Fig. 5
figure 5

Evolution of the polydispersity index over time

Full size image
Fig. 6
figure 6

Molecular weight distribution of the product

Full size image
$$W^{k} (x) = \frac{{y^{k} (xy^{k} )^{{z^{k} }} e^{{ - xy^{k} }} }}{{e^{{\ln [\varGamma (z^{k} + 1)]}} }},\quad k = 1,2, \ldots ,N_{s} .$$
(29)

In Eq. (29), Wk represents the mass fraction of polymer chains with a degree of polymerization x, produced at the catalyst site of “k”, “y” and “z” which are Schultz–Flory parameters defined as

$$z^{k} = \frac{{{\raise0.7ex\hbox{${\xi_{1}^{k} }$} \!\mathord{\left/ {\vphantom {{\xi_{1}^{k} } {\xi_{0}^{k} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\xi_{0}^{k} }$}}}}{{{\raise0.7ex\hbox{${\xi_{2}^{k} }$} \!\mathord{\left/ {\vphantom {{\xi_{2}^{k} } {\xi_{1}^{k} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\xi_{1}^{k} }$}} - {\raise0.7ex\hbox{${\xi_{1}^{k} }$} \!\mathord{\left/ {\vphantom {{\xi_{1}^{k} } {\xi_{0}^{k} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\xi_{0}^{k} }$}}}},\quad y^{k} = \frac{{z^{k} + 1}}{{{\raise0.7ex\hbox{${\xi_{2}^{k} }$} \!\mathord{\left/ {\vphantom {{\xi_{2}^{k} } {\xi_{1}^{k} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\xi_{1}^{k} }$}}}}.$$
(30)

Hence, for a multi-site catalyst, the overall MWD is determined by the weighted sum of all polymer fractions produced over the Ns catalyst active sites:

$$W_{t} (x) = \sum\limits_{k = 1}^{{N_{s} }} {W^{k} (x)\left( {\frac{{\xi_{1}^{k} }}{{\sum\limits_{k = 1}^{{N_{s} }} {\xi_{1}^{k} } }}} \right)} ,$$
(31)

In which \(\sum\nolimits_{k = 1}^{{N_{s} }} {\xi_{1}^{k} }\) accounts for the total polymer mass produced over the Ns catalyst active sites.

Figure 7 depicts the variations of melting flow index over time. According to this figure, the final value of MFI is stabilized at 18 for the first reactor, which is very close to the actual plant measurements, and 17 for the second reactor, demonstrating a 7% error in comparison with the actual measurements.

Fig. 7
figure 7

Change of MFI over time

Full size image

In the following figures, the dynamic behavior of the reactors is studied to survey the effects of changes in catalyst concentration and monomer concentration, which are the major possible effective loads of the system.

The effects of 25% increase in catalyst on the temperature of both reactors are illustrated in Fig. 8. It could be seen that the increase in the amount of catalyst leads to the increase of the exothermic reaction rates and, therefore, the temperatures rise to new steady-state values.

Fig. 8
figure 8

The effect of 25% increase of catalyst on the temperature

Full size image

This increase in the amount of catalyst also affects other parameters of the reactors, such as monomer concentrations. The variations in ethylene concentration are plotted in Fig. 9 for the first and the second reactors. As expected, the increase of reaction rates results in the reduction of ethylene concentration.

Fig. 9
figure 9

The effect of 25% increase of catalyst on the ethylene concentration

Full size image

The effects of 50% increase in ethylene concentration on the temperature and weight average molecular weight of the reactors have also been examined. As indicated in Fig. 10, this will lead to a small increase in temperature of the reactors for a short period of time due to the rise in reaction rate. Moreover, the temperatures start to diminish to a value less than the previous steady-state values. The variations of the weight average molecular weight are shown in Fig. 11. It could be seen that the average molecular weights increase with a rise in ethylene concentration. The aforementioned results stipulate the most significant disturbances of the process that the devised control system is expected to reject to maintain the optimum conditions.

Fig. 10
figure 10

The effect of 50% increase in ethylene concentration on the temperature

Full size image
Fig. 11
figure 11

The effect of 50% increase in ethylene concentration on the average molecular weight

Full size image

Figure 12 depicts the effects of catalyst active site distribution on the molecular weight distribution in the first and the second reactors. Three distinct active sites ratios are employed for both reactors to demonstrate that the MWD shifts to larger molecular weights as this ratio (S1/S2) increases.

Fig. 12
figure 12

The effect of distribution of catalyst active site on the molecular weight distribution in a the first reactor, b the second reactor

Full size image

Closed-loop simulation

To control the bed height and the bed temperature of each reactor, the modified model proposed in Sect. 3 is employed (considering the heat exchangers and variable bed height) and a feedback control structure is devised according to conventional PID (proportional–integral–derivative) control algorithm. The PID controllers are frequently the best choice for industrial control systems due to their simplicity and proven applicability. If properly tuned, PID controllers can be robust in addressing uncertainties and disturbances. In this study, tuning of the controllers is accomplished based on closed-loop Ziegler–Nichols procedure. This algorithm is one of the most common tuning methods of PID controllers in which the gain of proportional controller is increased until sustained oscillations arise in the output signal. Controller parameters such as proportional gain, reset time and derivative value are calculated from the ultimate gain and sustained oscillation period. Following this procedure, a quarter decay wave ratio is achieved. It should be mentioned that the parameters tuned by Ziegler–Nichols method are used as starting values, while the exact values adopted in this work are the results of further fine tunings. The parameters of the controllers are demonstrated in Table 5.

Table 5 Parameters of controllers and characteristics of closed-loop response for load rejection
Full size table

In this section, the dynamic closed-loop behavior of the process, consisting of two serried reactors and their accompanied heat exchangers, in response to some predefined disturbances are presented and analyzed. To observe the performance of the proposed control configuration and applied PI controllers, multiple distinct sources of disturbances (changes in monomer concentration, catalyst feed rate and cooling water temperature) have been introduced to the process. The set points for the first and the second reactor temperatures, and their bed heights are 360 K and 353 K, and 700 cm and 1400 cm, respectively. Figure 13 illustrates the effects of a 25% increment in ethylene concentration of the first reactor feed on controlled and manipulated variables. As can be seen in these figures, the controllers performed satisfactorily, and the temperature and height of each bed reached their desired values with no considerable overshoot or offset.

Fig. 13
figure 13

Deviations of controlled and manipulated variables for a the first reactor bed height, b temperature, c the second reactor bed height, and d temperature, due to 25% increase in the feed ethylene concentration

Full size image

Figure 14 indicates the temperatures of the first and second bed responses to a 25% increase in catalyst feed rate. This figure shows that the characteristic responses of temperature controllers are acceptable and proper in industrial scale.

Fig. 14
figure 14

Deviations of a the first and b the second bed temperature from its steady-state value due to 25% increase in the catalyst feed rate

Full size image

Also, a 10 °C step change in the value of the cooling water temperature is applied and the closed-loop responses of the process are presented in Fig. 15. The temperature controllers are again able to reject the influences of this disturbance and maintain the temperatures at their set points. Since the deviations from the set points were insignificant during the simulation, the bed height responses for the last two disturbances are not reported here.

Fig. 15
figure 15

Deviations of a the first and b the second bed temperatures from its steady-state value due to a 10 °C step change to the cooling water temperature

Full size image

Conclusion

A dynamic model was proposed for the production of LLDPE, utilizing a serried reactor configuration in industrial scale. To serve this purpose, a well-mixed model was employed for both reactors, and a two-site kinetic model was considered for the heterogeneous Ziegler–Natta catalyst. These models contributed to a significant progress in our knowledge of the fundamental parameters of both reactors including monomer concentration, production rate, reactor temperature as well as polymer properties such as molecular weight distribution and polydispersity index. Model validation was investigated by comparing the actual plant data with the results in terms of MFI, and it was found to be satisfactory in this case. The effects of catalyst amount, monomer concentration and the catalyst active site distribution on reactor parameters and polymer properties were also surveyed in open-loop state. Based on the examination of the results obtained by our model, we can state that the presented model can be adopted as a predictive tool to study the reactor behavior in the presence of disturbances. The dynamic analysis of the open-loop system is employed to design a PID controller for adjusting the cooling water flow rate of heat exchangers and the reactor effluent flow rates to maintain the temperatures and the heights of each bed at their set points. For closed loop state, the model was modified for control purposes, and the dynamics of heat exchangers were taken into account. Also, the bed level of each reactor was considered as a variable. The suggested feedback closed-loop system has shown a good performance for load rejection in an acceptable period of time.