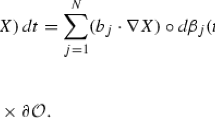Abstract
We introduce the uniqueness, existence, \(L_p\)-regularity, and maximal Hölder regularity of the solution to semilinear stochastic partial differential equation driven by a multiplicative space-time white noise:
where \(\lambda > 0\). The function \(\sigma (u)\) is either bounded Lipschitz or super-linear in u. The noise \(\dot{W}\) is a space-time white noise. The coefficients a, b, c depend on \((\omega ,t,x)\), and \({{\bar{b}}}\) depends on \((\omega ,t)\). The coefficients \(a,b,c,{\bar{b}}\) are uniformly bounded, and a satisfies ellipticity condition. The random initial data \(u_0 = u_0(\omega ,x)\) is nonnegative. To establish the \(L_p\)-regularity theory, we impose an algebraic condition on \(\lambda \) depending on the nonlinearity of the diffusion coefficient \(\sigma (u)\). For example, if \(\sigma (u)\) has Lipschitz continuity, linear growth, and boundedness in u, \(\lambda \) is assumed to be less than or equal to 1; \(\lambda \in (0,1]\). However, if \(\sigma (u) = |u|^{1+\lambda _0}\) with \(\lambda _0\in [0,1/2)\), \(\lambda \) is taken to be less than 1; \(\lambda \in (0,1)\). Under those conditions, the uniqueness, existence, and regularity of the solution are obtained in stochastic \(L_p\) spaces. Also, we have the maximal Hölder regularity by employing the Hölder embedding theorem. For example, if \(\lambda \in (0,1]\) and \(\sigma (u)\) has Lipschitz continuity, linear growth, and boundedness in u, for \(T<\infty \) and \(\varepsilon >0\),
On the other hand, if \(\lambda \in (0,1)\) and \(\sigma (u) = |u|^{1+\lambda _0}\) with \(\lambda _0\in [0,1/2)\), for \(T<\infty \) and \(\varepsilon >0\),
It should be noted that if \(\sigma (u)\) is bounded Lipschitz in u, the Hölder regularity of the solution is independent of \(\lambda \). However, if \(\sigma (u)\) is super-linear in u, the Hölder regularities of the solution are affected by nonlinearities, \(\lambda \) and \(\lambda _0.\)
Similar content being viewed by others
Data Availibility Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Bertini, L., Cancrini, N., Jona-Lasinio, G.: The stochastic Burgers‘ equation. Commun. Math. Phys. 165(2), 211–232 (1994)
Da Prato, G., Debussche, A., Temam, R.: Stochastic Burgers‘ equation. Nonlinear Differ. Equ. Appl. 1(4), 389–402 (1994)
Da Prato, G., Gatarek, D.: Stochastic Burgers’ equation with correlated noise. Stochs. Int. J. Prob. Stoch. Process. 52(1–2), 29–41 (1995)
Gyöngy, I.: Existence and uniqueness results for semilinear stochastic partial differential equations. Stoch. Process. Appl. 73(2), 271–299 (1998)
Gyöngy, I., Rovira, C.: On stochastic partial differential equations with polynomial nonlinearities. Stochs. Int. J. Prob. Stoch. Process. 67(1–2), 123–146 (1999)
Gyöngy, I., Rovira, C.: On \(L_p\)-solutions of semilinear stochastic partial differential equations. Stoch. Process. Appl. 90(1), 83–108 (2000)
León, J.A., Nualart, D., Pettersson, R.: The stochastic Burgers‘ equation: finite moments and smoothness of the density. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 3(03), 363–385 (2000)
Englezos, N., Frangos, N.E., Kartala, X.I., Yannacopoulos, A.N.: Stochastic Burgers’ pdes with random coefficients and a generalization of the Cole-Hopf transformation. Stoch. Process. Appl. 123(8), 3239–3272 (2013)
Catuogno, P., Olivera, C.: Strong solution of the stochastic Burgers equation. Appl. Anal. 93(3), 646–652 (2014)
Lewis, P., Nualart, D.: Stochastic Burgers’ equation on the real line: regularity and moment estimates. Stochastics 90(7), 1053–1086 (2018)
Röckner, M., Sobol, Z.: Kolmogorov equations in infinite dimensions: well-posedness and regularity of solutions, with applications to stochastic generalized Burgers equations. Ann. Probab. 34(2), 663–727 (2006)
Crighton, D.G., Dowling, A.P., Ffowcs-Williams, J., Heckl, M., Leppington, F., Bartram, J.F.: Modern methods in analytical acoustics lecture notes (1992)
Ladyzhenskaia, O.A. Solonnikov, V.A., Ural’tseva, N.N.: Linear and quasi-linear equations of parabolic type, Vol. 23, American Mathematical Soc., (1968)
Dix, D.B.: Nonuniqueness and uniqueness in the initial-value problem for Burgers’ equation. SIAM J. Math. Anal. 27(3), 708–724 (1996)
Bekiranov, D.: The initial-value problem for the generalized Burgers’ equation. Differ. Integral Equ. 9(6), 1253–1265 (1996)
Tersenov, A.S.: On the generalized Burgers equation. Nonlinear Differ. Equ. Appl. 17(4), 437–452 (2010)
Gomez, A., Lee, K., Mueller, C., Wei, A., Xiong, J.: Strong uniqueness for an spde via backward doubly stochastic differential equations. Stat. Probab. Lett. 83(10), 2186–2190 (2013)
Krylov, N.V.: An analytic approach to spdes. Stoch. Partial Differ. Equ Six Perspect. 64, 185–242 (1999)
Krylov, N.V.: On a result of C. Mueller and E. Perkins, Probab. Theory Relat. Fields 108 (4) (1997) 543–557
Krylov, N.V.: On SPDE‘s and superdiffusions, Ann. Probab. (1997) 1789–1809
Mueller, C.: Long time existence for the heat equation with a noise term. Probab. Theory Relat. Fields 90(4), 505–517 (1991)
Burdzy, K., Mueller, C., Perkins, E.: Nonuniqueness for nonnegative solutions of parabolic stochastic partial differential equations. Illinois J. Math. 54(4), 1481–1507 (2010)
Mytnik, L.: Weak uniqueness for the heat equation with noise, Ann. Probab. (1998) 968–984
Mytnik, L., Perkins, E.: Pathwise uniqueness for stochastic heat equations with Hölder continuous coefficients: the white noise case. Probab. Theory Relat. Fields 149(1–2), 1–96 (2011)
Walsh, J.B.: An introduction to stochastic partial differential equations, in: École d’Été de Probabilités de Saint Flour XIV-1984, Springer, (1986), 265–439
Xiong, J.: Super-Brownian motion as the unique strong solution to an SPDE. Ann. Probab. 41(2), 1030–1054 (2013)
Choi, J., Han, B.: A regularity theory for stochastic partial differential equations with a super-linear diffusion coefficient and a spatially homogeneous colored noise. Stoch. Process. Appl. 135, 1–30 (2021)
Han, B., Kim, K.: Boundary behavior and interior Hölder regularity of solution to nonlinear stochastic partial differential equations driven by space-time white noise. J. Differ. Equ. 269, 9904–9935 (2020)
Mueller, C.: The critical parameter for the heat equation with a noise term to blow up in finite time, Ann. Probab. (2000) 1735–1746
Grafakos, L.: Modern Fourier analysis, Vol. 250, Springer, (2009)
Krylov, N.V.: Lectures on elliptic and parabolic equations in Sobolev spaces, Vol. 96, American Mathematical Soc., (2008)
Krylov, N.V.: Maximum principle for spdes and its applications, stochastic differential equations: theory and applications: a Volume in Honor of Professor Boris L Rozovskii, World Scientific, (2007), 311–338
Krylov, N.: Introduction to the theory of diffusion processes, Providence, (1995)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2021R1C1C2007792) and the BK21 FOUR (Fostering Outstanding Universities for Research) funded by the Ministry of Education (MOE, Korea) and National Research Foundation of Korea (NRF)
Rights and permissions
About this article
Cite this article
Han, BS. A regularity theory for stochastic generalized Burgers’ equation driven by a multiplicative space-time white noise. Stoch PDE: Anal Comp 11, 1123–1163 (2023). https://doi.org/10.1007/s40072-022-00256-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40072-022-00256-8
Keywords
- Stochastic partial differential equation
- Nonlinear
- Super-linear
- Stochastic generalized Burger’s equation
- Space-time white noise
- Hölder regularity