Rare event simulation via importance sampling for linear SPDE’s

Abstract

The goal of this paper is to develop provably efficient importance sampling Monte Carlo methods for the estimation of rare events within the class of linear stochastic partial differential equations. We find that if a spectral gap of appropriate size exists, then one can identify a lower dimensional manifold where the rare event takes place. This allows one to build importance sampling changes of measures that perform provably well even pre-asymptotically (i.e. for small but non-zero size of the noise) without degrading in performance due to infinite dimensionality or due to long simulation time horizons. Simulation studies supplement and illustrate the theoretical results.

Appendices

Appendix A: Proof of Lemma 5.5

Before proving Lemma 5.5 let us define some useful quantities. Set

$$\begin{aligned} \beta _{0}(x)&=\left[ \rho _{1}(x)\left| B^{\star } D_{x}F_{1}(x)\right| ^{2}_{H}-\rho _{1}^{2}(x)\left| B^{\star } D_{x}F_{1}(x)\right| ^{2}_{H}\right] \end{aligned}$$

and notice that $\rho _{1}\in [0,1]$, guarantees that $\beta _{0}(x)\ge 0$. In addition, let us define

$$\begin{aligned} \gamma _{1}=\mathcal {G}^{{\varepsilon }}[F_{1}](x)=-{\varepsilon }\alpha _{1}. \end{aligned}$$

By the argument of Lemma 4.1 of [5] applied to $\mathcal {G}^{\varepsilon }[U^{\delta ,\eta }](x)$ and (5.2) we get

$$\begin{aligned} \mathcal {G}^{{\varepsilon }}[U^{\delta ,\eta },U^{\delta }](x)\ge&\frac{1-\eta }{2}\left( 1-\frac{{\varepsilon }}{\delta }\right) \beta _{0}(x)+(1-\eta )\rho _{1}(x)\gamma _{1} \nonumber \\&+\frac{\eta -2\eta ^{2}}{2}\rho _{1}^{2}(x) \left| B^{\star } D_{x}F_{1}(x)\right| ^{2}_{H} \end{aligned}$$

(A.1)

for all $x\in H$. The lower bound for the operator $\mathcal {G}^{{\varepsilon }}[U^{\delta ,\eta },U^{\delta }](x)$, given by (A.1), will be based on a separate analysis for three different regions that are determined by level sets of $V_{1}(x)=|<x,e_{1}>|^{2}$.

Let $\kappa \in (0,1)$ to be chosen, $\alpha \in (0,1-\kappa )$ and consider K such that $\frac{e^{-K}}{e^{-K}+1}=\frac{3}{4}$, i.e., $K=-\ln 3<0$. Let us also assume ${\varepsilon }\in (0,1)$ . Then, we define

$$\begin{aligned} B_{1}= & {} \left\{ x\in H: V_{1}(x)\le {\varepsilon }^{\kappa +\alpha }, \kappa \in (0,1),\alpha \in (0,1-\kappa ) \right\} \\ B_{2}= & {} \left\{ x\in H: {\varepsilon }^{\kappa +\alpha }\le V_{1}(x)\le {\varepsilon }^{\kappa }+ \left( {\varepsilon }^{\kappa }-{\varepsilon }K\right) \right\} \\ B_{3}= & {} \left\{ x\in H: {\varepsilon }^{\kappa }+ \left( {\varepsilon }^{\kappa }-{\varepsilon }K\right) \le V_{1}(x)\le L^{2}\right\} \end{aligned}$$

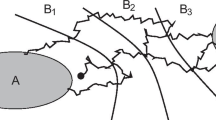
Lemma 5.5 is a direct consequence of Lemmas A.1, A.2 and A.3 that treat the regions $B_{1}, B_{3}$ and $B_{2}$ respectively.

Lemma A.1

Assume that $x\in B_{1}$, $\delta =2{\varepsilon }$, $\eta \le 1/2$ and ${\varepsilon }\in (0,1)$. Then, up to an exponentially negligible term

$$\begin{aligned} \mathcal {G}^{\varepsilon }[U^{\delta ,\eta },U^{\delta }](x)\ge 0. \end{aligned}$$

Proof

In this region, we are guaranteed that $F_{1}(x)> F_{2}^{{\varepsilon }}$. Indeed, we have that

$$\begin{aligned} F_{1}(x)- F_{2}^{{\varepsilon }}&\ge \frac{\alpha _{1}}{\lambda _1^2}\left( {\varepsilon }^{\kappa }-{\varepsilon }^{\kappa +\alpha }\right) > 0 \end{aligned}$$

since ${\varepsilon }<1$ and $\alpha \in (0,1)$. Hence, we have that

$$\begin{aligned} -\frac{1}{2{\varepsilon }}\left[ F_{1}(x)- F_{2}\right] \le -\frac{1}{2{\varepsilon }}\left[ {\varepsilon }^{\kappa }\left( 1-{\varepsilon }^{\alpha }\right) \right] =-\frac{1-{\varepsilon }^{\alpha }}{2{\varepsilon }^{1-\kappa }} \end{aligned}$$

This immediately implies that the term involving the weight $\rho _{1}$ is exponentially negligible. Since $\beta _{0}(x)\ge 0$ and $\eta \le 1/2$, all other terms are non-negative, and the result follows. $\square$

Lemma A.2

Assume that $x\in B_{3}$, $\delta =2{\varepsilon }$, $\eta \le 1/4$ and that ${\varepsilon }^{1-\kappa }\in (0,\alpha _{1}/2\lambda _1^2)$. Then, we have

$$\begin{aligned} \mathcal {G}^{{\varepsilon }}[U^{\delta ,\eta },U^{\delta }](x)\ge 0. \end{aligned}$$

Proof

In this region we have that $V(x)\ge 2{\varepsilon }^{\kappa }-{\varepsilon }\beta K>0$ for ${\varepsilon }$ small enough. Moreover, since $K=-\ln 3$ is chosen such that

$$\begin{aligned} \frac{\epsilon ^{-K}}{\epsilon ^{-K}+1}=\frac{3}{4} \end{aligned}$$

we obtain that for $x\in B_{3}$, $\rho _{1}(x)\ge 3/4$. We have the following inequalities

$$\begin{aligned} \mathcal {G}^{{\varepsilon }}[U^{\delta ,\eta },U^{\delta }](x) \ge&(1-\eta )\frac{1}{4}\rho _{1}(x)(1-\rho _{1}(x))\left| B^{\star } D_{x} F_{1}(x)\right| ^{2}_{H}+(1-\eta )\rho _{1}(x)\gamma _{1}\\&\quad +\,\frac{1}{2}\left( \eta -2\eta ^{2}\right) \left| \rho _{1}(x)B^{\star } D_{x}F_{1}(x)\right| ^{2}\\&\ge (1-\eta )\left[ \rho _{1}(x)(1-\rho _{1}(x))\frac{\alpha _{1}^{2}}{\lambda _1^2}V_{1}(x) -{\varepsilon }\alpha _{1} \rho _{1}(x)\right] \\&\quad +\,2\left( \eta -2\eta ^{2}\right) \rho _{1}^{2}(x) \frac{\alpha _{1}^{2}}{\lambda _1^2}V_{1}(x)\\&\ge (1{-}\eta )\left[ \frac{\alpha ^{2}_{1}}{4\lambda _1^2}V_{1}(x) {-}{\varepsilon }\alpha _{1}\right] \rho _{1}(x){+} \frac{3\frac{\alpha ^{2}_{1}}{\lambda _1^2}}{2}\left( \eta {-}2\eta ^{2}\right) \rho _{1}(x)V_{1}(x)\\&\ge (1{-}\eta )\left[ \frac{\alpha ^{2}_{1}}{4\lambda _1^2}\left( 2{\varepsilon }^{\kappa }{-}{\varepsilon }K\right) {-}{\varepsilon }\alpha _{1}\right] \rho _{1}(x){+} \frac{9\alpha ^{2}_{1}}{16\lambda _1^2}\eta \left( 2{\varepsilon }^{\kappa }-{\varepsilon }K\right) \\&\ge (1-\eta )\alpha _{1}\left[ \frac{\alpha _{1}}{2\lambda _1^2}{\varepsilon }^{\kappa } -{\varepsilon }\right] \rho _{1}(x)+ \frac{9\alpha ^{2}_{1}}{8\lambda _1^2}\eta {\varepsilon }^{\kappa }\\&\ge 0 \end{aligned}$$

In the third inequality we used the fact that $\rho _{1}(x)\ge 3/4$ for $x\in B_{3}$. In the next inequality we used that $\eta \le 1/4$ and that for $x\in B_{3}$, $V_{1}(x)\ge 2{\varepsilon }^{\kappa } -{\varepsilon }K$. Lastly, in the last inequality, we used that $K<0$ and that $0<{\varepsilon }^{1-\kappa }<\alpha _{1}/(2\lambda _{1}^{2})$. This concludes the proof of the lemma. $\square$

Lemma A.3

Assume that $x\in B_{2}$, $\eta \le 1/4$ and set $\delta =2{\varepsilon }$. Let ${\varepsilon }>0$ be small enough such that ${\varepsilon }^{1-\kappa }\le \frac{\alpha _{1}}{2\lambda _{1}^{2}}$. Then we have that

$$\begin{aligned} \mathcal {G}^{{\varepsilon }}[U^{\delta ,\eta },U^{\delta }](x)\ge&0. \end{aligned}$$

Proof

This is the most problematic region, since one cannot guarantee that $\rho _{1}$ is exponentially negligible or of order one. We distinguish two cases depending on whether $\rho _{1}(x)>1/2$ or $\rho _{1}(x)\le 1/2$.

For the case $\rho _{1}(t,x)>1/2$, one can just follow the proof of Lemma A.2. Then, one immediately gets that $\mathcal {G}^{{\varepsilon }}[U^{\delta ,\eta },U^{\delta }](x)\ge 0$.

Let us now study the case $\rho _{1}(x)\le 1/2$. Here we need to rely on the positive contribution of $\beta _{0}(x)$. Dropping other terms on the right that are not possibly negative, we obtain from (A.1) that

$$\begin{aligned} \mathcal {G}^{{\varepsilon }}[U^{\delta ,\eta },U^{\delta }](x)&\ge (1-\eta )\frac{\beta }{4}\rho _{1}(x)(1-\rho _{1}(x))\left| B^{\star } D_{x} F_{1}(x)\right| ^{2}_{H}+(1-\eta )\rho _{1}(x)\gamma _{1}\\&\ge (1-\eta )\frac{\beta }{8}\rho _{1}(x)\left| B^{\star } D_{x} F_{1}(x)\right| ^{2}_{H}+(1-\eta )\rho _{1}(x)\gamma _{1} \end{aligned}$$

where we used $\rho _{1}(t,x)\le 1/2$. Recalling now the definitions of $D_{x}F_{1}(x)$ and $\gamma _{1}$, we subsequently obtain

$$\begin{aligned} \mathcal {G}^{{\varepsilon }}[U^{\delta ,\eta },U^{\delta }](t,x)&\ge (1-\eta )\left[ \frac{\alpha _{1}^{2}}{2\lambda _{1}^{2}}V(x)-{\varepsilon }\alpha _{1}\right] \rho _{1}(x)\\&\ge (1-\eta )\alpha _{1}\left[ \frac{\alpha _{1}}{2\lambda _{1}^{2}}{\varepsilon }^{\kappa }-{\varepsilon }\right] \rho _{1}(x)\ge 0 \end{aligned}$$

In the last inequality we used that for $x\in B_{2}$ $V(x)\ge {\varepsilon }^{\kappa }$ and that ${\varepsilon }>0$ is small enough such that ${\varepsilon }^{1-\kappa }\le \frac{\alpha _{1}}{2\lambda _{1}^{2}}$. This concludes the proof of the lemma. $\square$

Appendix B: Galerkin approximation

The goal of this section is to get an explicit bound in terms of ${\varepsilon },T$ and the eigenvalues of the difference of $X^{\varepsilon }(t)$ and its finite dimensional Galerkin approximation, see also [9] for general bounds. Our goal is not to present the most general result possible, but rather to point out the issues related for the problem studied in thus paper in the simplest situation possible. For $N \in \mathbb {N}$ let $H_N$ be the finite dimensional space ${ span }\{e_k\}_{k=1}^N$. Let $\Pi _N: H \rightarrow H_N$ be the projection operator onto this space. That is, for any $x \in H$,

$$\begin{aligned} \Pi _N x = \sum _{k=1}^N \left\langle x,e_k\right\rangle _H e_k. \end{aligned}$$

Definition B.1

Letting $A_N := \Pi _N A$, the $N^{\text {th}}$ Galerkin approximation for $X^{\varepsilon }$ is defined to be the solution to N-dimensional SDE

$$\begin{aligned} {\left\{ \begin{array}{ll} dX_N^{\varepsilon }(t) = (A_N X_N^{\varepsilon }(t) + \Pi _N B u(X_N^{\varepsilon }(t)) )dt + \sqrt{{\varepsilon }} \Pi _N B d w(t) \\ X_N^{\varepsilon }(0) = \Pi _N x. \end{array}\right. } \end{aligned}$$

(B.1)

Given that in this paper, u represents the control being applied which turns out to be affine, we may, for the purposes of this section, embed this into A. We will do so and thus from now on set $u=0$. The same conclusions hold when $u\ne 0$.

Theorem B.2

For any initial condition $x \in H$ and any ${\varepsilon }>0$, $T>0$,

$$\begin{aligned} {\mathbb {E}}\sup _{t \le T}|X^{\varepsilon }(t) - X^{\varepsilon }_N(t)|_H^2 \le |(I-\Pi _N)x|_H + \sqrt{{\varepsilon }} CT\left( \sum _{k=N+1}^\infty \lambda _{k}^{2}\alpha _k^{-\gamma } \right) ^{1/2}, \end{aligned}$$

(B.2)

for some constant $C<\infty$. The limit as $N \rightarrow +\infty$ is zero but it is not uniform with respect to initial conditions in bounded subsets of H. The limit is uniform with respect to initial condition in the compact set $\{x\in H: |(-A)^\eta x|_H \le R\}$ for any $\eta > 0$.

Before proving this theorem in generality, we study the special case of the stochastic convolution.

Lemma B.3

For any $T>0$, $p\ge 1$, $\frac{1}{2}<\gamma <1$ the Galerkin approximations of the stochastic convolution converge in $L^p(\Omega ;C([0,T];H))$ and there exists a constant $C=C(p,\gamma )$ such that

$$\begin{aligned} {\mathbb {E}}\sup _{t \le T} \left| (I-\Pi _N)\int _0^t e^{(t-s)A}Bdw(s) \right| _H^p \le C T \left( \sum _{k=N+1}^\infty \lambda _{k}^{2}\alpha _k^{-\gamma } \right) ^{p/2}. \end{aligned}$$

(B.3)

Proof

We use the stochastic factorization method (see [4]) which is based on the following identity. For any $s<t$, $0<\alpha <1$

$$\begin{aligned} \int _s^t (t-\sigma )^{\alpha - 1} (\sigma -s)^{-\alpha } d\sigma = \frac{\pi }{\sin (\alpha \pi )}. \end{aligned}$$

(B.4)

We then write the stochastic convolution as

$$\begin{aligned} \int _0^t e^{(t-s)A}B d w(s)= & {} \frac{\sin (\alpha \pi )}{\pi }\int _0^t (t-\sigma )^{\alpha -1} e^{(t-\sigma )A} Y_\alpha (\sigma )d\sigma \end{aligned}$$

(B.5)

$$\begin{aligned} Y_\alpha (\sigma )= & {} \int _0^\sigma (\sigma -s)^{-\alpha }e^{(\sigma -s)A} B d w(s). \end{aligned}$$

(B.6)

Let $\frac{1}{2}<\gamma <1$ and $p\ge 1$. We then choose $0<\alpha < \frac{1-\gamma }{2}$ and calculate that

$$\begin{aligned} {\mathbb {E}}\left| (I-\Pi _N) Y_\alpha (\sigma ) \right| _H^2 = \int _0^\sigma s^{-2\alpha } \sum _{k=N+1}^\infty \lambda _{k}^{2} e^{-2\alpha _k s} ds \end{aligned}$$

We use the identity $\sup _{x>0} x^\gamma e^{-x} =: C_\gamma <+\infty$ to show that

$$\begin{aligned} e^{-2\alpha _k s} \le \frac{e^{-\alpha _1 s}}{s^\gamma \alpha _k^\gamma } \end{aligned}$$

and it follows that there exists $C=C(\alpha ,\gamma )$ such that

$$\begin{aligned} {\mathbb {E}}|(I-\Pi _N)Y_\alpha (\sigma )|_H^2 \le \left( \int _0^\infty s^{-2\alpha -\gamma } e^{-\alpha _1 s} ds\right) \sum _{k=N+1}^\infty \lambda _{k}^{2}\alpha _k^{-\gamma } \le C\sum _{k=N+1}^\infty \lambda _{k}^{2}\alpha _k^{-\gamma }. \end{aligned}$$

By the Burkholder–Davis–Gundy inequality, for any $p\ge 2$,

$$\begin{aligned} {\mathbb {E}}|(I-\Pi _N) Y_\alpha (\sigma )|_H^p \le C \left( \sum _{k=N+1}^\infty \lambda _{k}^{2}\alpha _k^{-\gamma } \right) ^{p/2}. \end{aligned}$$

By applying the Hölder inequality to (B.5)

$$\begin{aligned} \left| (I-\Pi _N) \int _0^t e^{(t-s)A}dw(s)\right| _H^p\le & {} \left( \int _0^t (t-\sigma )^{\frac{p(\alpha -1)}{p-1}} e^{-\frac{p\alpha _1(t-\sigma )}{p-1}} d\sigma \right) ^{p-1}\\&\left( \int _0^t |Y_\alpha (\sigma )|_H^p d\sigma \right) . \end{aligned}$$

If we choose p large enough so that $\frac{p(\alpha -1)}{p}>-1$, then the first integral converges and is bouned for all $t>0$ and

$$\begin{aligned} {\mathbb {E}}\sup _{t \le T}\left| (I-\Pi _N) \int _0^t e^{(t-s)A}dw(s)\right| _H^p \le C T \left( \sum _{k=N+1}^\infty \lambda _{k}^{2}\alpha _k^{-\gamma } \right) ^{p/2}. \end{aligned}$$

We can lower p by using Jensen’s inequality. $\square$

Proof of Theorem B.2

First, we observe that in the case being considered

$$\begin{aligned} |X^{\varepsilon }(t) - X^{\varepsilon }_N(t)|_H = |X^{\varepsilon }(t) - \Pi _N X^{\varepsilon }(t)|_H. \end{aligned}$$

So, we can write

$$\begin{aligned} X^{\varepsilon }(t) - \Pi _N X^{\varepsilon }(t) = (I-\Pi _N)e^{At}x + \sqrt{{\varepsilon }} (I-\Pi _N)\int _0^t e^{(t-s)A}B d w(s). \end{aligned}$$

We know that

$$\begin{aligned} \left| (I-\Pi _N)e^{At}x \right| _H \le |(I-\Pi _N)x|_H \rightarrow 0. \end{aligned}$$

If $x \in (-A)^{-\eta }(H)$, then

$$\begin{aligned} |(I-\Pi _N)x|_H = |(I-\Pi _N)(-A)^{-\eta }(-A)^\eta x|_H \le \alpha _{N+1}^{-\eta }|(-A)^\eta x|_H. \end{aligned}$$

The stochastic convolution term can be made small by Lemma B.3. We can combine these estimates to conclude that

$$\begin{aligned} {\mathbb {E}}\sup _{t \le T}|X^{\varepsilon }(t) - X_N^{\varepsilon }(t)|_H \le |(I-\Pi _N)x|_H + \sqrt{{\varepsilon }} CT\left( \sum _{k=N+1}^\infty \lambda _{k}^{2}\alpha _k^{-\gamma } \right) ^{1/2}. \end{aligned}$$

The above expression converges to 0 and the convergence is uniform for initial conditions x satisfying $|(-A)^{\eta }x|_H \le R$. $\square$

We conclude this section with two relevant remarks.

Remark B.4

The previous theorem shows that $X^{\varepsilon }(t)$ and its Galerkin approximation $X^{\varepsilon }_N(t)$ are pathwise close, but also that the Galerkin approximation’s accuracy for fixed n and ${\varepsilon }$ decreases as time T increases. This is not a failure of our estimation. The difference $X^{\varepsilon }(t) - X^{\varepsilon }_N(t)$ is a Markov process that is exposed to the noise $\sqrt{{\varepsilon }}(I-\Pi _N)B d w(t)$. While this noise is degenerate in H, it is nondegenerate on the the subspace $(I-\Pi _N)(H)$. We can guarantee by standard arguments that for fixed n and ${\varepsilon }$ and with probability one $X^{\varepsilon }(t)$ and $X^{\varepsilon }_N(t)$ will deviate from each other arbitrarily far on an infinite time horizon.

Remark B.5

In Theorem B.2, we claimed that the convergence of the Galerkin approximations is uniform if the initial conditions x are regular enough. In fact, over long time periods, the regularity of the initial conditions does not matter. This is because

$$\begin{aligned} |(I-\Pi _N)e^{tA} x|_H \le e^{-\alpha _N t} |x|_H. \end{aligned}$$

Therefore we can have uniform convergence on bounded sets in $D \subset H$ as long as we consider the estimate

$$\begin{aligned} \sup _{x \in D}{\mathbb {E}}\sup _{t_0\le t \le T} \left| X^{\varepsilon }(t) - X^{\varepsilon }_N(t) \right| _H^2 \end{aligned}$$

for some $t_0>0$.