Abstract
To investigate the effectiveness of using fiber reinforced polymer (FRP) sheets in confining heat-damaged columns, 15 circular RC column specimens were tested under axial compression. The effects of heating duration, stiffness and thickness of the FRP wrapping sheets were examined. Two specimen groups, six each, were subjected to elevated temperatures of 500 °C for 2 and 3 h, respectively. Eight of the heat-damaged specimens were wrapped with unidirectional carbon and glass FRP sheets. Test results confirmed that elevated temperatures adversely affect the axial load resistance and stiffness of the columns while increasing their ductility and toughness. Full wrapping with FRP sheets increased the axial load capacity and toughness of the damaged columns. A single layer of the carbon sheets managed to restore the original axial resistance of the columns heated for 2 h yet, two layers were needed to restore the axial resistance of columns heated for 3 h. Glass FRP sheets were found to be less effective; using two layers of glass sheets managed to restore the axial load carrying capacity of columns heated for 2 h only. Confining the heat-damaged columns with FRP circumferential wraps failed in recovering the original axial stiffness of the columns. Test results confirmed that FRP-confining models adopted by international design guidelines should address the increased confinement efficiency in heat-damaged circular RC columns.
Similar content being viewed by others
1 Introduction
Compared to other construction materials, concrete provides superior fire resistance as a result of its low thermal conductivity and incombustible nature. Proper design of typical concrete structures for fire resistance simply requires selection of appropriate member dimensions and concrete covers. Yet, exposure of concrete to long duration fires or elevated temperatures adversely affects its compressive and flexural strengths, modulus of elasticity and volume stability among other mechanical properties (Chan et al. 1999; Luo et al. 2000; Husem 2006; Arioz 2007, 2009; Netinger et al. 2011). Significant losses in the compressive strength of concrete ranging between 50 and 70% are typically encountered at temperatures above 550 °C (Georgali and Tsakiridis 2005). Depending on the extent of fire-induced damages and the residual load-bearing capacities, it is often both technically and economically viable to repair and reuse concrete structures after fire.
An extensive variety of repair and strengthening techniques can be implemented to rehabilitate fire-damaged concrete elements and structures. Traditional repair schemes for deficient or damaged concrete columns involve the use of concrete or steel jackets (Lin et al. 1995; Campione 2012; Ramirez et al. 1997; Xiong et al. 2011) which incurs additional weight and interrupts the function of the structure during the somewhat lengthy repair process. Compared to more conventional repair materials, the use of externally bonded fiber reinforced polymer (FRP) composites offers numerous advantages including, but not limited to, their high strength-to-mass ratio, high stiffness-to-mass ratio, excellent corrosion resistance, adaptability, non invasive nature and ease of application which minimizes functionality interruption. As such, the numerous applications of FRP composites in repairing reinforced concrete (RC) structural elements have been widely investigated over the past three decades. Very few experimental investigations have recently examined the potential of using FRP composites to repair heat-damaged RC columns (Yaqub and Bailey 2011a, b, 2012; Yaqub et al. 2011, 2013; Bisby et al. 2011; Bailey and Yaqub 2012; Tahir et al. 2013; Al-Nimry et al. 2013; Roy et al. 2014, 2016; Al-Kamaki et al. 2015). Most of the test columns were unstressed during heating, cooling and testing despite the fact that columns are expected to be stressed up to 50% of their capacity during any fire incident. To this end, Al-Kamaki et al. (2015) applied an axial compressive loading of 30% of the maximum compressive strength at ambient temperature while exposing the test columns to elevated temperatures. Available research results (Yaqub and Bailey 2011a, b, 2012; Yaqub et al. 2011, 2013; Bisby et al. 2011; Bailey and Yaqub 2012; Tahir et al. 2013; Al-Nimry et al. 2013; Roy et al. 2014, 2016; Al-Kamaki et al. 2015) indicated that jacketing heat-damaged columns with unidirectional FRP sheets may, depending on the cross sectional shape, restore the axial strength of the columns. FRP jacketing has been found efficient in enhancing the ductility, deformation and energy dissipation capacities of heat-damaged columns. To restore the original axial strength of square heat-damaged RC columns; Al-Nimry et al. (2013) proposed the use of externally bonded longitudinal FRP plates confined with circumferential carbon FRP sheets over the full column height. Glass and carbon FRP jacketing showed no significant effect on the axial stiffness of wrapped heat-damaged columns (Yaqub and Bailey 2011a, b, 2012; Yaqub et al. 2011, 2013; Bisby et al. 2011; Al-Nimry et al. 2013). Yaqub et al. (2013) proposed the use of both ferrocement and FRP jackets to restore the strength, stiffness and ductility of fire-damaged RC columns. Compared to the confinement strengthening systems provided by high-strength fiber-reinforced concrete, ferrocement and steel plate jacketing; Roy et al. (2016) found that FRP jacketing was the most effective in restoring the compressive strength and energy dissipation of heat-damaged RC short columns.
The present study explores the feasibility of using external FRP confinement in restoring or enhancing the axial strength and stiffness of circular RC columns that have been exposed to a pre-defined heat level. Effects of the heating duration/level, stiffness and thickness of the unidirectional FRP sheets used to confine the heat-damaged columns were among the parameters investigated.
2 Experimental Program
2.1 General
A total of 15 RC column specimens having a 192 mm diameter and 900 mm length were cast, wet-cured and tested under axial loading. Three unheated specimens were designated as undamaged controls: two identical specimens (CH0-A and CH0-B) were tested without jacketing whereas the third (CH0-C1L) was confined using carbon fiber reinforced polymer (CFRP) sheets before testing. The remaining 12 specimens were equally divided into two groups (CH2 and CH3), six specimens each, and subjected to elevated temperatures of 500 °C for 2 (CH2 specimens) and 3 h (CH3 specimens). In each of these groups, two specimens were designated as damaged controls (CHi-A and CHi-B) where the subscript i indicates the heating duration in hours (2 or 3 h). Four heat-damaged specimens in each of the two groups CH2 and CH3 were repaired using FRP jackets. All repair schemes were intended to provide external confinement for the heat-damaged columns. The columns were wrapped with unidirectional FRP sheets with the direction of fibers oriented parallel to the circumference of the cross section. Both carbon and glass FRP sheets were used as follows:
-
Two heat-damaged specimens in each of the two groups CH2 (heated for 2 h) and CH3 (heated for 3 h) were wrapped using CFRP sheets: specimen CHi-C1L wrapped with a single layer and specimen CHi-C2L wrapped with two layers of the fabric sheets where the subscript i indicates the heating duration in hours. According to ACI 440.2R (2008) the CFRP sheets, with a thickness of 0.131 mm, provide an FRP reinforcement ratio of 0.00273 and 0.00546 for the single and double layer wraps, respectively.
-
Two heat-damaged specimens in each of the two groups CH2 and CH3 were confined using glass fiber reinforced polymer (GFRP) sheets: specimens CHi-G1L and CHi-G2L were wrapped using one and two layers of the 0.17 mm thick sheets, respectively. According to ACI 440.2R (2008), the single and double layer GFRP wraps provide an FRP reinforcement ratio of 0.00354 and 0.00708, respectively.
The specimens’ designations and relevant test parameters are summarized in Table 1.
2.2 Layout and Detailing of Test Specimens
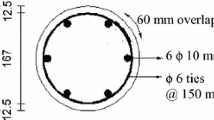
The general layout and reinforcement details of the test specimens are shown in Fig. 1. All column specimens were designed as short columns with a circular cross section of 192 mm diameter and an unsupported length of 900 mm. Six steel deformed rebars of 10-mm diameter were used for the main column reinforcement providing a longitudinal reinforcement ratio of 0.017. Transverse reinforcement was provided using 6-mm diameter deformed ties at a uniform spacing of 150 mm. The ties were provided with a 60 mm overlap as shown in Fig. 1.
2.3 Materials
Crushed coarse limestone aggregates (with a maximum aggregate size of 9.5 mm) and a mixture of crushed fine limestone and silica sands (60% fine limestone and 40% silica sand by volume) were used with ordinary Portland cement (Type I) to prepare the concrete mix for the columns following ACI 211.1-91 (1991) mix design procedure. The concrete mix was designed using a water-to-cement ratio of 0.54. A super plasticizer was used at 0.5% by cement weight to achieve a slump of about 75 mm.
Five concrete batches were used to cast the column specimens with an average 28-day compressive strength (f c´) of 41 MPa. To determine concrete strength of the columns (both unheated and heated) at time of testing; additional concrete cylinders (150 × 300 mm) were prepared, wet-cured, heated (as applicable) and tested with their companion column specimens: cylinders tested, without heating, resulted in an average compressive strength of about 52 MPa. Heat-damaged cylinders that were subjected to the same regimen of elevated temperatures and air cooling experienced by the CH2 and CH3 columns exhibited substantial reductions in the compressive strength of concrete of 62.5 and 67.3%, respectively. Average compressive strength values of 19.5 and 17 MPa were recorded for heating durations of 2 and 3 h, respectively. In fact, elevated temperatures of about 550 °C have been reported to cause substantial reductions in concrete compressive strength reaching up to 70% of strength at ambient temperature (Georgali and Tsakiridis 2005).
The average yield stress of the main steel reinforcement was 451 MPa with about 18% elongation at failure. To assess the effect of elevated temperatures on the mechanical properties of the hot-rolled steel reinforcement, longitudinal steel bars were extracted from two of the control heated columns (CH2-A and CH3-A) and were tested. Exposure to the 2- and 3-h heating durations of 500 °C resulted in minor losses (2.2 and 7.5%) in tensile yield strength of the steel reinforcement. Actually, Neves et al. (1996) showed that temperatures below 600 °C have a negligible effect on the tensile strength of hot-rolled steel after air cooling.
The geometric and physical properties of the carbon and glass FRP fabric sheets used for repair are summarized in Table 2. It should be noted that for the same number of FRP wrapping sheets the confinement modulus E l (given by Eq. (1), which is a measure of the stiffness of the confining FRP jacket, of the carbon FRP jacket amounts to 2.4 times that of the glass FRP jacket.
where E f is the tensile elastic modulus of FRP sheets, n the number of FRP layers, t f the nominal thickness of one FRP layer and D the diameter of the column cross section.
2.4 Specimen-Preparation
Test specimens were cast into PVC plastic molds. All specimens were cast in a vertical position, de-molded 72 h after casting, and then wet-cured using moist canvas for 28 days. The test specimens were transferred to the open lab environment wherein superficial defects and pores were repaired using a commercially available dental plaster material in preparation for heating. On the average, the test specimens were heated 2 months after casting. Although the moisture content of the concrete was not measured at the time of heating, it is expected that the moisture content of the surface concrete was that of the ambient with a relative humidity of about 60%.
Twelve specimens were subjected to temperatures of 500 °C: six for 2 h and six for 3 h using an electrical furnace that automatically controls the temperature and time of exposure. The furnace size (1.7 × 1.0 × 0.5 m) allowed heating four column specimens and six cylinders at a time as shown in Fig. 2. Column end surfaces were insulated, using Rockwool, to protect the end surfaces themselves as areas of direct axial loading and minimize possible heat transfer to the concrete core through the longitudinal column reinforcement that terminates at or near the column bottom and top surfaces.
Fire testing, even when following standard fire tests (e.g. ASTM E119), does not reflect or simulate a realistic fire scenario. In a typical fire, the outer layers of concrete members are expected to reach 500 °C in a few minutes and 950 °C in 1 h while lower temperature levels are encountered at inner layers (Nassif et al. 1995). The heating level and duration adopted for this research were intended, in view of the relatively large scale of the test specimens; to allow the core concrete to reach temperature levels close to that at the column surface thereby inducing significant reductions in the mechanical properties of the concrete (Al-Nimry et al. 2013; Chen et al. 2009; Jau and Huang 2008) while maintaining the integrity and viability of the heated columns for repair using FRP jacketing alone without the need to use any kind of intervention prior to FRP wrapping. Figure 3 displays the furnace temperature history implemented in this study. Logistic and safety measures dictated the long ramp period of about 10 h preceding the maximum exposure temperature. The slow heating process adopted in the current study (refer to Fig. 3), in conjunction with the extended heating for 2 or 3 h, leads to reduced internal temperature gradients and allows for discarding the thermal gradient-induced stresses.
To ensure safe handling of the heated specimens, the cover of the furnace was slightly opened and columns were allowed to cool for about 12 h inside the furnace before removal. The heated columns were then removed and placed in the lab, with an ambient temperature of about 23 °C, in preparation for the repair process which started almost 1 month after heating.
On the average, the specimens were tested 2 months after heating. Given this time and in view of the relatively large specimen sizes, negligible differences in moisture content of the different columns were expected at the time of testing.
Eight of the heat-damaged specimens were repaired using CFRP and GFRP products according to the repair schemes shown in Table 1. Surface preparation and wrapping followed the manufacturer’s specifications using the dry lay-up technique. The FRP sheets were cut to the perimeter (plus 100 mm extra for overlapping along the circumference conforming to manufacturer’s specifications) and height dimensions of the columns. FRP sheets were wrapped around the column with the main fibers oriented in the hoop direction. A 25 mm gap was maintained between the two column ends and the FRP jacket to avoid direct axial loading of the jacket itself. Prior to testing, column ends were capped to ensure their vertical alignment and allow for uniform loading during testing. The confined heat-damaged specimens were tested almost 1 month after jacketing to allow for proper curing of the impregnation resin.
2.5 Test Setup and Instrumentation
On the average, columns were 4 months of age at the time of testing. All specimens were tested under an axial concentric loading using a 4000 kN (in compression) capacity universal testing machine. The axial loading was increased gradually using displacement control at a displacement rate of 0.5 mm/min.
Each of the test specimens was instrumented with four linear variable displacement transducers (LVDTs). Axial and circumferential strains were measured using a displacement measurement system (compressometer–extensometer) that was specifically devised for this test. The compressometer included two aluminum rings that were fixed at a distance of 225 mm from top and bottom of the column specimen as shown in Fig. 4. The longitudinal displacement transducer L1, with a linear stroke of 50 mm, was mounted onto the compressometer rings to measure axial strains over a gage length of 450 mm. The extensometer included an aluminum ring located halfway between the two compressometer rings and fixed at mid height of the test specimen. To measure hoop strains, LVDT L2, with a linear stroke of 10 mm, was placed in the form of a hoop onto the extensometer. Two horizontal LVDTs (L3 and L4), placed 90° apart, were used to measure the lateral displacements at mid height of the column. Test data was collected at a rate of five readings per second using an automatic data acquisition system.
3 Test Results
3.1 General
The characteristics of the axial load–displacement (F–Δ) curves for the control, heat-damaged and repaired test columns are summarized in Table 3. The secant stiffness value reported in the table identifies the slope of the line radiating from the origin and intersecting the F–Δ curve at an axial load corresponding to 50% of the maximum load-carrying capacity of the column specimen. The tabulated Δ max value defines the axial displacement value corresponding to a point located on the post-yield part of the actual curve wherein the axial load drops by 20%, indicating a state of strength failure. On the other hand, the toughness values represent the area under the F–Δ curve up to the state of strength failure. The global displacement ductility (μ) in the table represents the ratio of Δ max to Δ y where Δ y is the yield displacement. To determine the yield displacement value; the actual F–Δ curve was idealized with a bi-linear curve using an iterative procedure: an initial value is chosen for the yield force F y such that this value does not exceed the maximum axial resistance attained during the test (F u ) and that the point with a force level of 0.6F y exists on the actual F–Δ curve. A line is then drawn from the origin to the yield point passing through the point with an ordinate of 0.6F y . The second segment of the bi-linear curve extends from the yield point to the point indicating strength failure (i.e. with an ordinate of 0.8F u ) as shown in Fig. 5. The final value of F y is determined using an iteration procedure such that the area under the idealized bi-linear curve approximates (with a maximum difference of 5%) that under the actual F–Δ curve.
Table 4 summarizes the axial stress, axial and hoop strain values of the different test specimens. The tabulated axial stress values are computed using the axial load capacity (F u ) divided by the gross area of the concrete section only. The reported axial and hoop strains represent the maximum values corresponding to F u . Axial and hoop strains are calculated using axial and circumferential displacements at mid height of the column, obtained from the L1 and L2 readings, divided by the relevant gage lengths.
3.2 Failure Modes
Concrete crushed at the top end of all column specimens as a result of stress concentration in the end region (as the columns were cast with no enlargement of the cross section or additional FRP confinement near the ends) as can be seen in Figs. 6, 7, and 8. This of course may indicate that higher column strengths may be expected under more realistic conditions. The failure mode of the unheated specimens was almost sudden, preceded by cracks at about 85% of their ultimate resistance capacities. However, in the control heated specimens, cracks were noted at an earlier stage at about 50% of the ultimate load capacity signifying a more ductile type of failure.
As for the FRP wrapped specimens, crushing of concrete at column ends was followed by rupture of the FRP sheets. Rupture of the wrapping sheets was first noted at about 80% of the axial load capacity. The failure of column specimens wrapped with two layers of FRP sheets was more violent; explosive with a loud booming noise and without any prior warning accompanied by a sudden loss of axial strength. The failure was notably more violent in case of CFRP jackets as compared to GFRP jackets which could be associated with the lower ductility; higher stiffness and tensile strength of the carbon sheets as compared to glass sheets (see Table 2).
The FRP jackets exhibited satisfactory lamination, i.e. bonding between the two FRP layers did not fail. Post failure inspection of the ruptured FRP sheets revealed satisfactory adhesion to the epoxy: this was evident through visual examination of the inner surfaces of the wraps that were covered by a thin layer of concrete. Despite the fact that ties did not open, localized buckling of the longitudinal reinforcement was evident in locations of the crushed and disintegrated concrete in specimens CH2-B and CH3-B.
3.3 Heat-Damaged Specimens
Twelve specimens were subjected to elevated temperatures of 500 °C for 2 or 3 h. Elevated temperatures caused minor superficial damage to the specimens: lateral hairline cracks, parallel to transverse reinforcement, were noted. In fact, these micro surface shrinkage cracks were noted in most of the specimens before heating and became clearly visible after heating. Superficial spider cracks, being more concentrated over the middle two-thirds of the column height, were also visible. Moreover, the intensity of surface cracking increased with increasing heating duration which is believed to be caused by the development of internal stresses associated with differential expansion (Hertz 2003). Most of the heat-induced cracks healed with time and became hardly detectable at the time repair was initiated.
As expected for this level of heating (Yaqub and Ghani 2013; Hager 2014), the color of the heated concrete columns changed into whitish grey which is probably associated with oxidization of ferric compounds that may be found in the aggregate or sand.
The general effect of heating on the axial load–displacement response of the test columns is displayed in Fig. 9. Figure 10, on the other hand, presents the axial strength, secant stiffness, toughness and ductility of the heat-damaged specimens (both unwrapped and wrapped) as a percentage of the corresponding values of the relevant control specimens. Comparison of average test results of the two control specimens (CH0-A and CH0-B) and the four control heat-damaged specimens (CH2-A, CH2-B and CH3-A, CH3-B) presented in Table 3 and shown in Figs. 9 and 10a reveals that subjecting the column specimens to 500 °C for 2 and 3 h resulted in a reduction of about 46 and 54%, respectively in their axial strength. Yaqub and Bailey (2011a, b) and Yaqub et al. (2011) reported compressive strength losses of 42 and 44% in medium scale circular (ϕ 200 × 1000 mm) and square (200 × 200 × 1000 mm) RC columns respectively, as a result of heating to 500 °C. Losses of 55% in axial strength of rectangular (100 × 170 × 1000 mm) RC columns that have been exposed to 500 °C for 3 h were encountered by Al-Nimry et al. (2013). Higher losses in axial strength of circular (ϕ 204 × 750 mm) RC columns heated to 800 and 1000 °C for 2 h reaching up to 43 and 72%, respectively were also reported in literature (Al-Kamaki et al. 2015). As expected, differences in specimen sizes and shapes, material properties and heating regimens have a clear effect on the residual strength of heated columns.
The significant reductions in compressive strength of the control heat-damaged CH2 and CH3 columns were accompanied by more severe reductions in initial axial stiffness of about 69 and 74%, respectively as shown in Fig. 10b. Again, major reductions (63–83%) in the axial stiffness of medium scale RC columns with a variety of cross sectional shapes, as a result of heat exposure (500 °C), were also noted by other researchers (Yaqub and Bailey 2011a, b; Yaqub et al. 2011; Al-Nimry et al. 2013).
On the other hand, toughness of the control heat-damaged CH2 and CH3 specimens increased by 29 and 42%, respectively as a result of exposure to 500 °C for 2 and 3 h. The notable increase in concrete toughness upon exposure to elevated temperatures is well recognized among researchers (Zhang et al. 2000). Al-Nimry et al. (2013) noted an increase of about 20% in toughness, again computed as the area under the F–Δ curve, of rectangular RC columns upon heating to 500 °C for 3 h.
Associated with the enhancement in toughness, an increase in the axial deformation capacity and ductility of the control heat-damaged CH2 and CH3 columns was noticed wherein the Δ max values increased by about 112 and 159%, respectively and the ductility increased by 23 and 36%, respectively.
Inspection of Table 4 reveals that substantial increases in axial strains of 69 and 105% and in hoop strains of about 40 and 67% took place in the control columns heated for 2 and 3 h, respectively. This notable increase in deformation capacity of the heat-damaged columns is attributed to the heat-induced micro-cracking and the removal of water which makes concrete soft and more porous. As such, concrete that has been subjected to elevated temperatures is expected to exhibit more lateral dilation, as compared to unheated concrete, under axial compression.
Test results of the four control heated specimens indicate that the maximum axial resistance and stiffness were reduced by 14.4 and 17.4%, respectively as the exposure duration increased from 2 to 3 h. On the other hand, the maximum axial displacement attained by the columns heated for 3 h reached about 1.2 times that of the columns exposed to 500 °C for 2 h indicating an increase in ductility. Ductility and toughness of the CH3 columns increased by 11 and 9.7%, respectively as compared with columns heated for 2 h. The observed decrease in the axial strength and stiffness and the accompanying increase in toughness and ductility of concrete columns as a result of increasing exposure duration is consistent with available research results (Chen et al. 2009; Yaqub and Ghani 2013; El-Shaer 2014).
It was earlier noted that a brittle type of failure occurred in the control unheated specimens: the failure was of an explosive nature accompanied by sudden loss of axial resistance (Fig. 9). In fact, the test columns were designed to experience crushing before reaching the critical buckling load. The significant reductions in compressive strength and modulus of elasticity of the heated concrete were not large enough to induce buckling in the columns as verified by the nominal axial strength at zero eccentricity (P o ) and the critical buckling load (P c ) values of the four control heated specimens presented in Table 5. The tabulated P o and P c values were computed using ACI 318-14 (2014) taking into account the heat-induced reductions in concrete and steel strengths as determined in the laboratory (see Sect. 2.3). In addition, the gross moment of inertia (I g ) of the heated column cross section was reduced by 30% to reflect the effect of the heat-induced cracks on the P c value. The modulus of elasticity of heated concrete was also reduced by 40% in view of reported values by Bisby et al. (2011) and Tolintino et al. (2002). Moreover, the near-zero readings of the lateral L3 and L4 transducers recorded during testing confirm that column buckling did not take place. Albeit, compared to the unheated specimens, the CH2 and CH3 heat-damaged control columns exhibited a more ductile type of failure.
3.4 Repaired Heat-Damaged Columns
3.4.1 Columns Repaired Using CFRP Sheets
The axial load–displacement curves for the heat-damaged control columns are compared with those obtained for specimens wrapped with CFRP sheets in Fig. 11. Figure 11 clearly shows that full wrapping with CFRP sheets enhances the axial load resistance of heat-damaged columns. Table 3 and Fig. 10a show that using one layer of CFPP wraps increased the axial resistance of the CH2 and CH3 heat-damaged columns by 105 and 113%, respectively.
Using one layer of the CFRP wraps managed not only to restore the original compressive strength of column specimens exposed to 2 h of heating but also exceeded the original F u value by 11%. For specimens heated for 3 h, the CFRP confinement nearly regained the full compressive strength of the original CH0 columns.
It is worth noting that the axial stiffness values of the CFRP confined columns were lower than those of the unwrapped heat-damaged specimens that have been subjected to the same heating regimen: compared to control heated specimens, a reduction in axial stiffness of about 33 and 24% was observed in CH2-C1L and CH3-C1L, respectively. This discrepancy in the axial stiffness values is probably associated with the non homogeneity of the concrete and the inevitable variability between the different column specimens. In fact, researchers (Bisby et al. 2011) confirmed that thermal exposure aggravates non homogeneities in the concrete. Moreover, confinement provided by the FRP wraps is not expected to be fully activated until reaching the maximum strength of the heated unconfined concrete after which continuous pressure is applied on the concrete core up to the failure (rupture) of the FRP wraps. Nonetheless, the overall effect of the thickness of the wrapping sheets on axial stiffness is still obvious. Within the same category of heating duration and type of FRP wraps, the enhancement in axial stiffness achieved when using two layers of the FRP wraps was notable: Compared to the case where a single layer of the CFRP sheets were used, an increase of 8.6 and 3.9% was recorded upon increasing the thickness of the wrap in the CH2 and CH3 specimens, respectively.
Confinement provided by the CFRP jackets resulted in significant enhancement of toughness of the heat-damaged columns. Toughness of the CH2 and CH3 columns confined with a single layer of carbon sheets was found to be 8.7 and 5.3 times toughness of the companion heat-damaged unwrapped columns.
Ductility of the CFRP wrapped heat-damaged columns (both CH2 and CH3) was found to be almost 2 times that of the control heat-damaged columns as a result of the uniform confinement provided by the FRP wraps for the micro-cracked heated concrete. The beneficial effect of FRP (both carbon and glass) confinement on the ductility of heated RC columns was noted by other researchers (Yaqub and Bailey 2011a, b; Yaqub et al. 2011, 2013) with higher enhancement in case of circular columns as compared to square columns.
The overall effect of the thickness of the wrapping sheets is obvious where using two layers of CFPR sheets had a beneficial effect on the axial resistance with an increase of about 24.5 and 36.7% for CH2 and CH3 columns, respectively. Upon increasing the thickness of the CFRP jackets, stiffness of the CH2 and CH3 columns increased by 8.6 and 3.9%; toughness by 49.9 and 82.3%; and deformation capacity (in terms of Δ max ) by 17.5 and 34.1%, respectively.
On the other hand, increasing the thickness of the CFRP jackets adversely affected the ductility of the heat-damaged specimens as can be seen in Fig. 10d. Compared to columns repaired using a single layer of the CFRP sheets, ductility of the CH2 and CH3 specimens repaired using a double-layered jacket decreased by about 12.2 and 13%, respectively.
Regarding the confinement effect provided through the CFRP wraps on the axial compressive stress of the heated columns, Table 4 shows that axial stresses of the confined CH2 and CH3 specimens reached 2–3 times the stress values of the companion control heated specimens. Axial stresses increased with increasing thickness of the CFRP jackets. This was accompanied by substantial increases in both axial (5–6 times for CH2 specimens and 4–5 times for CH3 specimens) and hoop strains (6–11 times for CH2 specimens and 5–9 times for CH3 specimens) measured at mid height of the columns. The significant enhancements in axial stress, axial and hoop strains of the FRP-confined heat-damaged columns is clearly associated with the increased lateral dilation of concrete after heating which causes higher tensile stresses in the FRP jackets and thereby provides higher restraining forces or confinement. For the same heating duration, strains also increased with increasing thickness of the FRP jacket. Effect of the FRP jackets was most pronounced on the hoop strain values wherein these strains reached 6 (for CH2-C1L) and 11 (for CH2-C2L) times those of the control heated CH2 specimens.
As for the confined unheated specimen CH0-C1L, wrapping the column with a single layer of carbon FRP sheets resulted in significant enhancements of axial resistance, deformation capacity, toughness and ductility. However, the axial stiffness of the CH0-C1L was lower than that of the companion unconfined CH0 specimens. The axial stress, axial and hoop strains of the CFRP jacketed unheated column increased significantly in comparison with the unconfined CH0 columns.
It is worth noting that CFRP confinement increased the axial resistance of the unheated column by about 40% whereas the same wrapping system induced substantially higher effects when used to confine heat-damaged columns. Increases of 105 and 113% in axial resistance of the CH2 and CH3 heat-damaged columns compared to control unheated specimens were encountered. This increased effectiveness of the FRP confinement when used to repair heat-damaged columns is attributed to the enhancement in lateral dilation of concrete after heating, which also increases with increased heating level or duration.
3.4.2 Columns Repaired Using GFRP Sheets
The axial load–displacement curves for the heat-damaged control columns are compared with those obtained for specimens wrapped with GFRP sheets in Fig. 12. Table 3, Figs. 10a and 12 show that using one layer of GFPP wraps increased the axial resistance of the CH2 and CH3 heat-damaged columns by 48 and 71%, respectively.
Similar to columns jacketed with CFRP sheets, a significant decrease of about 38 and 34% in the axial stiffness of the repaired CH2 and CH3 columns, respectively, was noted when compared to the unwrapped heat-damaged specimens.
Again, the overall effect of the thickness of the wrapping sheets is still obvious where using two layers of GFPR wraps increased the axial resistance of the CH2 and CH3 columns by 32 and 11.8%, respectively. Upon increasing the thickness of the GFRP jackets stiffness of the CH2 and CH3 columns increased by 11.8 and 14.4%; toughness by 29.9 and 26.1%; and deformation capacity (in terms of Δ max ) by 2.8 and 7.4%, respectively.
Increasing the thickness of the GFRP jackets adversely affected the ductility of the heat-damaged specimens. Compared to columns repaired using a single layer of the GFRP sheets, ductility of the CH2 and CH3 specimens repaired using a double layer jacket decreased by about 17 and 2.5%, respectively.
Comparing stress and strain values of the GFRP jacketed columns with relevant values of the control heated specimens presented in Table 4 shows that axial stresses, axial and hoop strains were significantly increased due to confinement: axial stress values were almost doubled upon using two layers of the confinement sheets for both the CH2 and CH3 specimens. Axial strain values of 4 and 3 times those of the corresponding CH2 and CH3 specimens were achieved. The effect on hoop strains was more pronounced; hoop strain values of 7 and 5 times those of the corresponding control heated CH2 and CH3 specimens were achieved. The axial stress, axial and hoop strain values of the GFRP jacketed columns increased with the increase in thickness of the jacket.
Nonetheless, using GFRP jackets with the lower confinement modulus proved to be, compared to CFRP jackets, less efficient in enhancing the axial behavior of the heat-damaged columns.
4 Theoretical Strength Predictions of FRP-Confined Columns
Extensive research efforts targeting the structural behavior of FRP-confined concrete columns over the past four decades have resulted in the development of design guidelines (ACI 440.2R 2008; CAN, CSA-S806-12 2012; fib 2001; TR 55 2012; CNR 2013) that provide predictive design equations for FRP-confined columns under ambient conditions. A large number of models, mostly empirical, correlating the increase in strength and ductility of FRP-confined concrete to the passive confining pressure provided by FRP jacketing systems have been developed (e.g. Shahawy et al. 2000; Xiao and Wu 2000; Harries and Kharel 2002; Lam and Teng 2003; Teng and Lam 2004; Carey and Harries 2005; Harajli 2006; Jiang and Teng 2007; Saenz and Pantelides 2007; Teng et al. 2007, 2009; Youssef et al. 2007; Lee and Hegemier 2009; Wu and Wang 2009; Benzaid et al. 2010; Chastre and Silva 2010; Cui and Sheikh 2010; Fahmy and Wu 2010; Pellegrino and Modena 2010; Dai et al. 2011; Liang et al. 2012; Wei and Wu 2012; Ozbakkaloglu and Lim 2013; Lim and Ozbakkaloglu 2014a, b, 2015a; Pham and Hadi 2014; Al Abadi et al. 2016; Lin et al. 2016). The basic parameter in these models is the lateral confining pressure (f l ) applied by the FRP jacket on the dilating concrete core shown in Fig. 13.
In fully wrapped circular columns, the ultimate confining pressure (f lu ) that can be exerted by the FRP jacket determines the strength gain for the confined concrete which is loaded in triaxial compression as given by the general form of Eq. 2:
where \( f_{cc}^{'} \) is the compressive strength of confined concrete, \( f_{co}^{'} \) the compressive strength of unconfined concrete also equal to 0.85 \( f_{c}^{'} \) and k 1 is an efficiency factor.
Most of the FRP-confining models for circular concrete sections estimate f lu in terms of the ultimate tensile strain of the fibers (ε fu ) obtained from flat coupon tests which is typically higher than the hoop rupture strain (ε h,rup ) of the FRP jacket with fibers oriented in the hoop direction (Shahawy et al. 2000; Xiao and Wu 2000; Lam and Teng 2003, 2004; Teng and Lam 2004; Ozbakkaloglu and Lim 2013; Lim and Ozbakkaloglu 2014a, b, 2015b; Wu and Jiang 2013; De Lorenzis and Tepfers 2003). Based on test results of 76 FRP wrapped plain concrete cylinders, Lam and Teng (2003) concluded that the strain efficiency or reduction factor, i.e. the ratio between the hoop rupture strain of the jacket to the material ultimate tensile strain, depends on the type of FRP material (carbon, glass or aramid). An average value of 0.63 was proposed when all specimens of the database were considered together. Wu and Jiang (2013) confirmed the vast variability in the strain efficiency values (0.274–1.133) published in the literature. Using a large experimental database of circular FRP-confined normal and high strength concrete specimens, Lim and Ozbakkaloglu (2014) developed the expression given in Eq. 3 for the strain efficiency factor. The expression denotes the influence of two key parameters on the hoop strain reduction factor (k ε,f ) namely; the compressive strength of unconfined concrete (\( f_{co}^{'} \)) and elastic modulus of confining fibers (E f ). Equation 3 can be used for FRP-confined concretes with \( f_{co}^{'} \) up to 120 MPa and confined by any FRP type.
where 100 GPa ≤ E f ≤ 640 GPa and with the units of the input parameters in MPa.
More recently, Lim and Ozbakkaloglu (2015b) tested 36 FRP-confined concrete cylinders (152 mm in diameter and 305 mm in height) that were specifically devised to examine the influence of concrete strength and type of FRP material on the hoop strain efficiency of FRP jackets. Test results, supplemented with 357 test results of FRP-confined concrete collected from the published literature, demonstrated the validity of the strain reduction factor expression given in Eq. (3).
Several researchers confirmed the wide variability in strength predictions offered by the existing FRP-confining models (Pellegrino and Modena 2010; De Lorenzis and Tepfers 2003; Bisby et al. 2005; Chaallal et al. 2006; Rocca et al. 2008). In a recent review of existing confining models, Ozbakkaloglu et al. (2013) assessed the performance of 88 models developed (between 1982 and 2011) to predict the axial stress–strain behavior of FRP-confined concrete in circular sections. To evaluate the performance of these models, a huge test database containing the test results of 730 FRP-confined concrete cylinders tested under axial compression was established. The top performing strength enhancement models were found to be those proposed by Lam and Teng (2003), Bisby et al. (2005) and Teng et al. (2007). The divergence in strength predictions of existing FRP-confining models is expected in view of the fact that these models are usually calibrated against limited sets of test data of plain concrete cylinders (rather than columns) with wide variations in test parameters. Moreover, the strength enhancement due to the FRP confinement is usually based on the strength of control concrete cylinders rather than the concrete strength of the unconfined column itself.
In this study, the actual axial load-carrying capacities of the FRP wrapped test columns (F u ) are compared with the values predicted by eight FRP-confining models including those proposed by ACI 440.2R (2008), CNR (2013), Lam and Teng (2003), Teng et al. (2009), Wu and Wang (2009), Fahmy and Wu (2010), Ozbakkaloglu and Lim (2013) and a more recent model suggested by Pham and Hadi (2014). As a matter of fact, the level of axial strength enhancement proposed by the ACI FRP-confining model (ACI 440.2R 2008) was recently adopted by Bisby et al. (2011) for fire-damaged concrete based on uniaxial compression tests of 33 unconfined and FRP-confined plain concrete cylinders that were heated to a range of elevated temperatures (300–686 °C) for 2–4 h and cooled to room temperature. A summary of the eight selected models is presented in Table 6 using a consistent set of parameters which may vary from the original model parameters.
Table 7 provides the theoretical axial strength capacities (F th ) of the FRP wrapped columns predicted by each of the eight confining models. It should be noted that the ultimate hoop strains reported in Table 4 do not represent the hoop rupture strain (ε h,rup ) of the FRP jacket as the tabulated values were measured at column mid height far away from the actual location of sheet rupture. Hence, it is expected that the FRP sheets have achieved higher strain values at the location of rupture, i.e. higher than the values attained at column mid height. This also means that hoop rupture strains for the carbon and glass FRP sheets are expected to exceed 0.004 (the minimum hoop strain value in Table 4) which is usually set by FRP-confining models as an upper value for ε h,rup . Accordingly, the value for the hoop rupture strain was set equal to the ultimate tensile strain of the fibers (ε fu ) multiplied by the strain efficiency factor given in the adopted confining model, if any. In absence of information on upper limits for the strain efficiency factor, a value of 0.6 ε fu (i.e. about 1 and 2% for carbon and glass sheets, respectively) was used. Moreover, in view of the testing conditions and dismissal of durability concerns, the environmental reduction factors (0.95 for carbon fibers and 0.75 for glass fibers) imposed by some of these models (ACI 440.2R. 2008; CNR 2013) on the ultimate rupture strain of the FRP reinforcement were disregarded.
Table 7 also presents the percentile error in strength predictions as given by Eq. 4:
Inspection of Table 7 shows that, compared to test results, all models predicted higher strength values for the CH0-C1L column which was wrapped without heating and generally lower values for the heat-damaged columns. This may indicate that the assumed confining efficiency of FRP jackets needs to be revised, i.e. increased for heated concrete which is expected to have an increased dilation capacity.
Based on average values of the absolute percentile error in model strength predictions of the FRP wrapped heat-damaged specimens presented in Fig. 14, it seems that the best performing models are those proposed by Ozbakkaloglu and Lim (2013), ACI 440.2R (2008) and Lam and Teng (2003). The strength values predicted by the ACI 440.2R (2008), Lam and Teng (2003) and Fahmy and Wu models (2010) for GFRP wrapped heat-damaged columns showed reasonable agreement with the actual strength values (average error of 4.6%) however, the same models highly underestimated the strength of CFRP wrapped heat-damaged columns (average error ranging from 14 to 21%). On the other hand, the strength enhancement of the CFRP wrapped columns predicted by the Ozbakkaloglu and Lim (2013) model were found to be in better agreement with the test results with an average error of 9.4% which indicates that even higher strain efficiency than predicted by Eq. (3) was attained. However, the same model overestimated the axial load carrying capacity of the GFRP wrapped heat-damaged columns by an average of 8.8% (error ranging from 2 to 19%).
5 Conclusions
This article presents test results of circular RC columns subjected to elevated temperatures and repaired using CFRP and GFRP fabric sheets. Both the carbon and glass jacketing schemes investigated herein provided effective confinement and thereby managed to enhance the axial strength, toughness, ductility and deformation capacity of the heat-damaged columns. The following points highlight the principal findings and conclusions derived from the experimental and analytical results:
-
1.
Subjecting circular RC columns to elevated temperatures of 500 °C for 2 and 3 h reduced their axial resistance by about 46 and 54%, respectively. The observed strength reductions are consistent with those reported in the literature.
-
2.
The substantial reduction in compressive strength of the heat-damaged columns was accompanied by a more severe deterioration in their axial stiffness of about 70%. Thermal exposure amplified the toughness, deformation capacity and global ductility of the columns.
-
3.
FRP jacketing enhanced the axial resistance, toughness and deformation capacities of the heat-damaged columns. The strength enhancement provided through the confining action of the hoop FRP sheets increased as the level of heat-induced damage increased. FRP jackets of sufficient stiffness (e.g. the double-layered carbon jackets used in this study) managed to restore and even exceed the original strength of the unheated columns but failed to reinstate their original stiffness.
-
4.
The increased stiffness or confinement modulus of the confining FRP jackets, induced by the increase in jacket thickness or the use of the more stiff carbon FRP sheets, resulted in further amplification of the axial load resistance, stiffness and toughness of the jacketed columns. Ductility however was adversely affected by the increase in jacket thickness.
-
5.
Compared to test results, the eight FRP-confining models used in this study including that of the ACI 440.2R (2008) generally under estimated the level of strength enhancement of the FRP-confined heat-damaged columns. Future research should target the development of confining models for heat-damaged concrete rather than low strength concrete as the confinement efficiency is highly dependent on the concrete ability to dilate under axial compression which is increased upon heating.
References
ACI 211.1-91. (1991). Standard practice for selecting proportions for normal, heavyweight and mass concrete (reapproved 2009). Farmington Hills, MI: American Concrete Institute.
ACI 318-14. (2014). Building code requirements for structural concrete (ACI 318-14) and commentary. Farmington Hills, MI: American Concrete Institute.
ACI 440.2R. (2008). Guide for the design and construction of externally bonded FRP systems for strengthening concrete structures. Farmington Hills, MI: American Concrete Institute.
Al Abadi, H., Abo El-Naga, H., Shaia, H., & Paton-Cole, V. (2016). Refined approach for modelling strength enhancement of FRP-confined concrete. Construction and Building Materials, 119(30), 152–174.
Al-Kamaki, Y., Al-Mahaidi, R., & Bennets, I. D. (2015). Experimental and numerical study of the behaviour of heat-damaged RC circular columns confined with CFRP fabric. Composite Structures, 133, 679–690.
Al-Nimry, H., Haddad, R., Afram, S., & Abdel-Halim, M. (2013). Effectiveness of advanced composites in repairing heat-damaged RC columns. Materials and Structures, 46(11), 1843–1860.
Arioz, O. (2007). Effects of elevated temperatures on properties of concrete. Fire Safety Journal, 42(8), 516–522.
Arioz, O. (2009). Retained properties of concrete exposed to high temperatures: Size effect. Fire and Materials, 33(5), 211–222.
Bailey, C., & Yaqub, M. (2012). Seismic strengthening of shear critical post-heated circular concrete columns wrapped with FRP composite jackets. Composite Structures, 94(3), 851–864.
Benzaid, R., Mesbah, H., & Chikh, N. (2010). FRP-confined concrete cylinders: Axial compression experiments and strength model. Journal of Reinforced Plastics and Composites, 29(16), 2469–2488.
Bisby, L. A., Chen, J. F., Li, S. Q., Stratford, T. J., Cueva, N., & Crossling, K. (2011). Strengthening fire-damaged concrete by confinement with fibre-reinforced polymer wraps. Engineering Structures, 33(12), 3381–3391.
Bisby, L. A., Dent, A. J. S., & Green, M. F. (2005). Comparison of confinement models for fiber-reinforced polymer-wrapped concrete. ACI Structural Journal, 102(1), 62–72.
Campione, G. (2012). Load carrying capacity of RC compressed columns strengthened with steel angles and strips. Engineering Structures, 40, 457–465.
CAN, CSA-S806-12. (2012). Design and construction of building structures with fibre-reinforced polymers. Mississauga, ON: Canadian Standards Association.
Carey, S. A., & Harries, K. A. (2005). Axial behavior and modeling of confined small-, medium-, and large-scale circular sections with carbon fiber reinforced polymer jackets. ACI Structural Journal, 102(4), 596–604.
Chaallal, O., Hassan, M., & LeBlanc, M. (2006). Circular columns confined with FRP: Experimental versus predictions of models and guidelines. ASCE Journal of Composites for Construction, 10(1), 4–12.
Chan, Y., Peng, G., & Anson, M. (1999). Residual strength and pore structure of high-strength concrete and normal strength concrete after exposure to high temperatures. Cement & Concrete Composites, 21(1), 23–27.
Chastre, C., & Silva, M. (2010). Monotonic axial behavior and modelling of RC circular columns confined with CFRP. Engineering Structures, 32(8), 2268–2277.
Chen, Y. H., Chang, Y. F., Yao, G. C., & Sheu, M. S. (2009). Experimental research on post-fire behaviour of reinforced concrete columns. Fire Safety Journal, 44(5), 741–748.
CNR. (2013). CNR-DT 200 R1/2013: Guide for the design and construction of externally bonded FRP systems for strengthening existing structures. Rome: Italian Research Council CNR Advisory Committee on Technical Recommendations for Construction.
Cui, C., & Sheikh, S. (2010). Analytical model for circular normal- and high-strength concrete columns confined with FRP. ASCE Journal of Composites for Construction, 14(5), 562–572.
Dai, J., Bai, Y., & Teng, J. (2011). Behavior and modeling of concrete confined with FRP composites of large deformability. ASCE Journal of Composites for Construction, 15(6), 963–973.
De Lorenzis, L., & Tepfers, R. (2003). Comparative study of models on confinement of concrete cylinders with fiber-reinforced polymer composites. ASCE Journal of Composites for Construction, 7(3), 219–237.
El-Shaer, M. (2014). Structural analysis for concrete columns subjected to temperature. Acta Technica Corviniensis-Bulletin of Engineering. Tome VII, Fascicule 2 (April–June) ISSN: 2067-3809.
Fahmy, M., & Wu, Z. (2010). Evaluating and proposing models of circular concrete columns confined with different FRP composites. Composites Part B Engineering, 41(3), 199–213.
Fib. (2001). Externally bonded FRP reinforcement for RC structures. Bulletin No. 14, Technical Report, Fédération internationale du Béton, Lausanne, Switzerland.
Georgali, B., & Tsakiridis, P. E. (2005). Microstructure of fire-damaged concrete. A case study. Cement & Concrete Composites, 27(2), 255–259.
Hager, I. (2014). Colour change in heated concrete. Fire Technology, 50(4), 945–958.
Harajli, M. H. (2006). Axial stress-strain relationship for FRP confined circular and rectangular concrete columns. Cement & Concrete Composites, 28(10), 938–948.
Harries, K. A., & Kharel, G. (2002). Behavior and modeling of concrete subject to variable confining pressure. ACI Materials Journal, 99(2), 180–189.
Hertz, K. D. (2003). Limits of spalling of fire-exposed concrete. Fire Safety Journal, 38(2), 103–116.
Husem, M. (2006). The effects of high temperature on compressive and flexural strengths of ordinary and high-performance concrete. Fire Safety Journal, 41(2), 155–163.
Jau, W. C., & Huang, K. L. (2008). A study of reinforced concrete corner columns after fire. Cement & Concrete Composites, 30(7), 622–638.
Jiang, T., & Teng, J. G. (2007). Analysis-oriented stress-strain models for FRP-confined concrete. Engineering Structures, 29(11), 2968–2986.
Lam, L., & Teng, J. G. (2003). Design-oriented stress-strain model for FRP-confined concrete. Construction and Building Materials, 17(6–7), 471–489.
Lam, L., & Teng, J. G. (2004). Ultimate condition of fiber reinforced polymer-confined concrete. ASCE Journal of Composites for Construction, 8(6), 539–548.
Lee, C., & Hegemier, G. (2009). Model of FRP-confined concrete cylinders in axial compression. ASCE Journal of Composites for Construction, 13(5), 442–454.
Liang, M., Wu, Z. M., Ueda, T., Zheng, J. J., & Akogbe, R. (2012). Experiment and modeling on axial behavior of carbon fiber reinforced polymer confined concrete cylinders with different sizes. Journal of Reinforced Plastics and Composites, 31(6), 389–403.
Lim, J. C., & Ozbakkaloglu, T. (2014a). Confinement model for FRP-confined high-strength concrete. ASCE Journal of Composites for Construction, 18(4), 1–19.
Lim, J. C., & Ozbakkaloglu, T. (2014b). Design model for FRP-confined normal and high-strength concrete square and rectangular columns. Magazine of Concrete Research, 66(20), 1020–1035.
Lim, J. C., & Ozbakkaloglu, T. (2015a). Unified stress-strain model for FRP and actively confined normal-strength and high-strength concrete. ASCE Journal of Composites for Construction, 19(4), 04014072-1–04014072-14.
Lim, J. C., & Ozbakkaloglu, T. (2015b). Hoop strains in FRP-confined concrete columns: Experimental observations. Materials and Structures, 48(9), 2839–2854.
Lin, C. H., Chen, S. T., & Yang, C. A. (1995). Repair of fire-damaged reinforced concrete columns. ACI Structural Journal, 92(4), 406–411.
Lin, G., Yu, T., & Teng, J. (2016). Design-oriented stress-strain model for concrete under combined FRP-steel confinement. ASCE Journal of Composites for Construction, 20(4), 04015084-1–04015084-11.
Luo, X., Sun, W., & Chan, S. (2000). Effect of heating and cooling regimes on residual strength and microstructure of normal strength and high-performance concrete. Cement and Concrete Research, 30(3), 379–383.
Nassif, A. Y., Burley, E., & Rigden, S. (1995). A new quantitative method of assessing fire damage to concrete structures. Magazine of Concrete Research, 47(172), 271–278.
Netinger, I., Kesegic, I., & Guljas, I. (2011). The effect of high temperatures on the mechanical properties of concrete made with different types of aggregates. Fire Safety Journal, 46(7), 425–430.
Neves, I., Rodrigues, J., & Loureiro, A. (1996). Mechanical properties of reinforcing and prestressing steels after heating. Journal of Materials in Civil Engineering, 8(4), 189–194.
Ozbakkaloglu, T., & Lim, J. C. (2013). Axial compressive behavior of FRP-confined concrete: Experimental test database and a new design-oriented model. Composites Part B Engineering, 55, 607–634.
Ozbakkaloglu, T., Lim, J. C., & Vincent, T. (2013). FRP-confined concrete in circular sections: Review and assessment of stress-strain models. Engineering Structures, 49, 1068–1088.
Pellegrino, C., & Modena, C. (2010). Analytical model for FRP confinement of concrete columns with and without internal steel reinforcement. ASCE Journal of Composites for Construction, 14(6), 693–705.
Pham, T. M., & Hadi, M. N. S. (2014). Confinement model for FRP confined normal- and high-strength concrete circular columns. Construction and Building Materials, 69, 83–90.
Ramirez, J. L., Barcena, J. M., Urreta, J. I., & Sanchez, J. A. (1997). Efficiency of short steel jackets for strengthening square section concrete columns. Construction and Building Materials, 11(5–6), 345–352.
Rocca, S., Galati, N., & Nanni, A. (2008). Review of design guidelines for FRP confinement of reinforced concrete columns of noncircular cross sections. ASCE Journal of Composites for Construction, 12(1), 80–92.
Roy, A., Sharma, U., & Bhargava, P. (2014). Strengthening of heat damaged reinforced concrete short columns. Journal of Structural Fire Engineering, 5(4), 381–398.
Roy, A., Sharma, U., & Bhargava, P. (2016). Confinement strengthening of heat-damaged reinforced concrete columns. Magazine of Concrete Research, 68(6), 291–304.
Saenz, N., & Pantelides, C. (2007). Strain-based confinement model for FRP confined concrete. Journal of Structural Engineering, 133(6), 825–833.
Shahawy, M., Mirmiran, A., & Beitelman, T. (2000). Tests and modeling of carbon-wrapped concrete columns. Composites Part B Engineering, 31, 471–480.
Tahir, M. F., Yaqub, M., Bukhari, I., Tufail, R. F., & Tahir, A. (2013). Effect of carbon fiber reinforced polymer confinement on the fire damaged and un-heated reinforced concrete square columns. Life Science Journal, 10(12s), 791–799.
Teng, J. G., Huang, Y. L., Lam, L., & Ye, L. (2007). Theoretical model for fiber reinforced polymer-confined concrete. ASCE Journal of Composites for Construction, 11(2), 201–210.
Teng, J. G., Jiang, T., Lam, L., & Luo, Y. Z. (2009). Refinement of a design-oriented stress-strain model for FRP-confined concrete. ASCE Journal of Composites for Construction, 13(4), 269–278.
Teng, J. G., & Lam, L. (2004). Behavior and modeling of fiber-reinforced polymer-confined concrete. Journal of Structural Engineering, 130(11), 1713–1723.
Tolentino, E., Lameiras, F. S., Gomes, A. M., Rigo da Silva, C. A., & Vasconcelos, W. L. (2002). Effects of high temperature on the residual performance of Portland cement concretes. Materials Research, 5(3), 301–307.
TR 55. (2012). Design guidance for strengthening concrete structures using fibre composite materials (3rd ed.) Technical Report No. 55, Concrete Society, Crowthorne, UK.
Wei, Y. Y., & Wu, Y. F. (2012). Unified stress-strain model of concrete for FRP-confined columns. Construction and Building Materials, 26(1), 381–392.
Wu, Y. F., & Jiang, J. F. (2013). Effective strain of FRP for confined circular concrete columns. Composite Structures, 95, 479–491.
Wu, Y. F., & Wang, L. M. (2009). Unified strength model for square and circular concrete columns confined by external jacket. ASCE Journal of Structural Engineering, 135(3), 253–261.
Xiao, Y., & Wu, H. (2000). Compressive behavior of concrete confined by carbon fiber composite jackets. ASCE Journal of Materials in Civil Engineering, 12(2), 139–146.
Xiong, G. J., Wu, X. Y., Li, F. F., & Yan, Z. (2011). Load carrying capacity and ductility of circular concrete columns confined by ferrocement including steel bars. Construction and Building Materials, 25(5), 2263–2268.
Yaqub, M., & Bailey, C. G. (2011a). Repair of fire damaged circular reinforced concrete columns with FRP composites. Construction and Building Materials, 25(1), 359–370.
Yaqub, M., & Bailey, C. G. (2011b). Cross sectional shape effects on the performance of post-heated reinforced concrete columns wrapped with FRP composites. Composite Structures, 93(3), 1103–1117.
Yaqub, M., & Bailey, C. G. (2012). Seismic performance of shear critical post-heated reinforced concrete square columns wrapped with FRP composites. Construction and Building Materials, 34, 457–469.
Yaqub, M., Bailey, C. G., & Nedwell, P. (2011). Axial capacity of post-heated square columns wrapped with FRP composites. Cement & Concrete Composites, 33(6), 694–701.
Yaqub, M., Bailey, C. G., Nedwell, P., Khan, Q. U. Z., & Javed, I. (2013). Strength and stiffness of post-heated columns repaired with ferrocement and fibre reinforced polymer jackets. Composites Part B Engineering, 44(1), 200–211.
Yaqub, M., & Ghani, U. (2013). Assessment of residual strength based on estimated temperature of post-heated RC columns. Mehran University Research Journal of Engineering and Technology, 32(1), 55–70.
Youssef, M. N., Feng, M. Q., & Mosallam, A. S. (2007). Stress-strain model for concrete confined by FRP composites. Composites Part B Engineering, 38(5–6), 614–628.
Zhang, B., Bicanic, N., Pearce, C. J., & Balabanic, G. (2000). Assessment of toughness of concrete subject to elevated temperatures from a complete load-displacement curve—Part 2: Experimental investigations. ACI Materials Journal, 97(5), 556–566.
Acknowledgements
The work presented in this article was funded by the Deanship of Research at Jordan University of Science and Technology under Grant No. 2015/45.
Funding
The Deanship of Scientific Research at Jordan University of Science and Technology funded the investigation subject of the paper. The sponsor had no role in the study design, in the collection, analysis and interpretation of data, in the writing of the report, and in the decision to submit the paper for publication.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Al-Nimry, H.S., Ghanem, A.M. FRP Confinement of Heat-Damaged Circular RC Columns. Int J Concr Struct Mater 11, 115–133 (2017). https://doi.org/10.1007/s40069-016-0181-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40069-016-0181-4