Numerical Simulation of Prestressed Precast Concrete Bridge Deck Panels Using Damage Plasticity Model

Abstract

This paper describes a three-dimensional approach to modeling the nonlinear behavior of partial-depth precast prestressed concrete bridge decks under increasing static loading. Six full-size panels were analyzed with this approach where the damage plasticity constitutive model was used to model concrete. Numerical results were compared and validated with the experimental data and showed reasonable agreement. The discrepancy between numerical and experimental values of load capacities was within six while the discrepancy of mid-span displacement was within 10 %. Parametric study was also conducted to show that higher accuracy could be achieved with lower values of the viscosity parameter but with an increase in the calculation effort.

1 Introduction

This paper presents the results of numerical simulations conducted using ABAQUS on hybrid partial-depth precast prestressed concrete (PPC) bridge deck panels using the concrete damage plasticity model to investigate the behavior and failure mechanism. The term “hybrid panel” in this paper describes a PPC panel that contains two different types of prestressing tendons: either epoxy-coated steel or carbon fiber reinforced polymer (CFRP) tendons at the panel edges, and uncoated steel tendons at the interior of the panel. Previous studies have shown that substitution of steel tendons with epoxy-coated steel could effectively reduce the occurrence of corrosion (Kobayashi and Takewaka 1984) and using FRP tendons as the addition of reinforced tendons, the ductility of the prestressed beams can be significantly improved (Saafi and Toutanji 1998).

2 Background

2.1 Bridge Deck Description

Partial-depth prestressed precast concrete deck panels span between girders and serve as stay-in-place (SIP) forms for a cast-in-place (CIP) concrete bridge deck. Typical panel geometries are 75–90 mm (3.0–3.5 in.) thick, 2.4 m (8 ft) long in the longitudinal direction of the bridge, and sufficiently wide to span between the girders in the bridge transverse direction. The panels are typically pretensioned with prestressing steel strands located at the panel mid-depth. Panels are placed adjacent to one another along the length of the bridge and typically are not connected to each other in the longitudinal bridge direction. After the panels are in place, the top layer of reinforcing steel is placed, and the CIP concrete portion of the deck [typically 125–140 mm (5.0–5.5 in) thick] is cast on top of the panels. At the bridge service state, the CIP concrete and SIP panels act as a composite deck slab.

2.2 Problem Statement

The most common problem reported with the use of partial-depth deck panels is reflective cracking on the top surface of the deck. Cracks in the transverse direction of the bridge may form at locations at which adjacent panels are placed (panel edges), while cracks in the longitudinal direction may form at the locations at which the panels are supported on the girders (panel ends).

The cause of the transverse reflective cracks is attributed primarily to the concentration of shrinkage and stress of CIP concrete at the joints between the precast panels (Hieber et al. 2005) (Fig. 1a). Transverse reflective cracks generally raise a deterioration concern because they permit the ingress of moisture and corrosion agents of steel reinforcement in the deck (Fig. 1b). When reflective cracks extend the full thickness of the CIP concrete layer, the ingress of moisture and corrosion agents can be concentrated at the panel edges (Fig. 1c), which has been observed to cause corrosion of steel prestressing tendons at the panel edges and spalling of concrete along the panel edges (Fig. 2) (Wieberg 2010; Sneed et al. 2010). Critical combinations of panel geometry, material properties, and reinforcement details can lead to long-term serviceability problems (Young et al. 2012; Wenzlick 2008).

Fig. 1

Spalling mechanism observed in PPC panels.

Fig. 2

Cracking and spalling at bridge deck panel joints.

3 Experimental Program

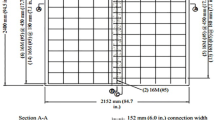
Testing data of an experimental program (Sneed et al. 2010) on six full-size partial-depth precast concrete deck panels were used to verify the numerical model developed in this study. The purpose of the experimental program was to investigate the structural behavior of the hybrid PPC panels as discussed previously. The dimension of the specimens was 75 mm thick, 2,440 mm length, and 2,440 mm width (Fig. 3 and Table 1). Three types of prestressed reinforcement were used in the experiments. Steel strand was 9.5 mm diameter, 7-wire, Grade 270 low-relaxation conforming to ASTM A 416 (2010). Epoxy-coated strand was 9.5 mm diameter, 7-wire, Grade 270 low-relaxation grit-impregnated conforming to ASTM A 882 (2010). Carbon fiber reinforced polymer (CFRP) tendons were No. 3 reinforcing bar. Table 2 summarizes the material properties of the prestressing reinforcement.

Fig. 3

Reinforcement details of specimens (mm).

Table 1 Test matrix.

Table 2 Material parameters (MPa/Psi).

The specimens were testing under displacement control, where a 1.25 mm increment was used until the failure of specimens. All six panels failed with concrete crushing in the compression zone near the mid-span. The testing setup is shown in Fig. 4.

Fig. 4

Test setup (mm).

4 Modeling Approach

4.1 Material Models

The finite element models of the tested specimens were built and analyzed with software ABAQUS. For linear elastic materials, at least two material constants are required: Young’s modulus (E) and Poisson’s ratio (v). For nonlinear materials, the steel and concrete uniaxial behaviors beyond the elastic range must be defined to simulate their behavior at higher strains. ABAQUS provides different types of concrete constitutive models including, (1) a smeared crack model; (2) a discrete crack model; and (3) a damage plasticity model (ABAQUS Theory Manual 2010). The concrete damage plasticity model, which can be used for modeling concrete and other quasi-brittle materials, was used in this study. This model combines the concepts of isotropic damage elasticity with isotropic tensile and compressive plasticity to model the inelastic behavior of concrete. The model assumes scalar (isotropic) damage and can be used for both monotonic and cyclic loading conditions. Elastic stiffness degradation from plastic straining in tension and compression is accounted for (Lubliner et al. 1989; Lee and Fenves 1998). Cicekli et al. (2007) and Qin et al. (2007) proved that damage plasticity model provides an effective method for modeling the concrete behavior in tension and compression.

4.1.1 Concrete Constitutive Model and Damage Indices

The concrete damage plasticity model requires input of parameters including the constitutive relationship of concrete, which can be customized by the user. This paper used the constitutive model of concrete developed by Zhenhai (2001) and Xue et al. (2010).

The stress–strain relationship as shown in Fig. 5 of concrete under uniaxial tension is described in Eq. (1). Damage is assumed to occur after the peak stress is reached.

Fig. 5

Concrete uniaxial tensile stress–strain curve.

$$y=\frac{x}{{\mathit{\alpha }}_t{(x-1)}^{1.7}+x}x\ge 1,$$

(1a)

$${\mathit{\alpha }}_t=0.312f_t^2,$$

(1b)

where α _t is decline curve parameters of concrete under uniaxial tension (if α _t  = 0 the curve becomes a horizontal line corresponding to fully plastic behavior while in case of α _t  = ∞ the curve becomes a vertical line corresponding to the fully brittle behavior). f _t is concrete tensile strength.

The stress–strain relationship as shown in Fig. 6 for concrete under uniaxial compression is described in Eq. (2).

Fig. 6

Concrete uniaxial compressive stress–strain curve.

$$y=\frac{x}{{\mathit{\alpha }}_d{(x-1)}^2+x}x\ge 1,$$

(2a)

$${\mathit{\alpha }}_d=0.157f_c^{0.785}-0.905,$$

(2b)

where α _d is the declining parameter of concrete under uniaxial compression; f _c is concrete compressive strength.

4.1.2 Other Data of Concrete Models

• (1) The dilation angle ψ is a ratio of vertical shear strain increment and strain increment, which is taken as 38 degrees.

• (2) Flow potential eccentricity ɛ is a small positive number that defines the rate at which the hyperbolic flow potential approaches its asymptote. This paper takes a value of 0.1.

• (3) National standard of the people’s republic of China (2002) recommend,

  $$-f_3/f_c^{\ast }=1.2+33{({\mathit{\sigma }}_1/{\mathit{\sigma }}_3)}^{1.8}$$

  (3)

  From FE model analysis, σ₁ = −16.66 Mpa, σ₃ = −1.73 Mpa, before the concrete cracks. So

  $$-f_3/f_c^{\ast }=1.2+33{(16.66/1.73)}^{1.8}=1.7585$$

  The ratio of initial equibiaxial compressive yield stress to initial uniaxial compressive yield stress σ _bo /σ _co was taken as 1.76.

• (4) The ratio of the second stress invariant on the tensile meridian, q(TM), to that on the compressive meridian K _c was taken as 2/3.

• (5) The viscosity parameter μ used for the visco-plastic regularization of the concrete constitutive equations in Abaqus/Standard was taken as 0.0005.

4.1.3 Prestressing Tendons

CFRP tendons were modeled as linear elastic while steel strand and epoxy-coated steel strand were modeled as bilinear hardening model (Fig. 7).

Fig. 7

Prestressed Reinforcement Material curve.

4.2 Finite Element Model Description

4.2.1 Symmetry

Because the PC panels investigated had two axes of symmetry, it was possible to represent the full slab by modeling only one fourth of the panel (Fig. 8). This reduced the analysis time (Wei et al. 2007). A linear elastic unit was also used to model the portion that stayed as elastic during testing.

Fig. 8

Modeling scheme of one fourth of the panel.

4.2.2 Element Type and Meshing Scheme

The 3D eight-node solid element C3D8 (Tuo 2008) was used to model the concrete. The T3D2 element was used to represent the prestressing strands or tendons. The model contained 6,144 nonlinear concrete elements, 3,072 three-dimensional linear elastic solid elements, and 432 prestressing tendons elements. CFRP tendons (or epoxy coated steel tendons) were divided into 96 elements. Element sizes were 25.4 mm × 38.1 mm × 12.7 mm. A meshed model is shown in Fig. 9.

Fig. 9

FE model of one fourth of the panel.

4.2.3 Bonding Between Reinforcement and Concrete

This is a technique used to place embedded nodes at desired locations with the constraints on translational degrees-of-freedom on the embedded element by the host element (Fig. 10). The rebar was modeled as embedded regions in the concrete in the interactive module, and making the concrete for the host. Thus, rebar elements can only had translations or rotations equal to those of the host elements surrounding them (Garg and Abolmaali 2009).

Fig. 10

Rebar was modeled as embedded regions.

4.2.4 Boundary Conditions

Due to symmetry, only a quarter of the panel was modeled as shown in Fig. 8. The nodes on symmetry surfaces were constrained in X and Y directions, respectively. At the supports, nodes were constrained in the z direction.

4.2.5 Prestressing Effect

Prestressing effect is usually modeled through either (1) initial strain or (2) initial temperature load. This study used initial temperature load to apply the prestressing load. The applied temperature t (°C) can be obtained from Eq. 4.

$$C=-\frac{\text{P}}{c·E·A}$$

(4)

C is coefficient of linear expansion taken as 1.0 × 10⁻⁵ (MPa/ °C); E is modulus elasticity of the tendon, in MPa; A is the cross-sectional area of the prestressing tendon in mm²; P (in N) is prestressing force calculated based on the recorded force during pretension process and with consideration of loss of prestressing effect.

4.2.6 Convergence Considerations

Convergence issues were resolved with the following considerations:

• (1) Loading steps were adjusted in consideration of the anticipated time of concrete cracking and the automatic time step was adopted.

• (2) Constitutive relationship was modified by introducing the coefficient of viscosity. A higher viscosity coefficient would make the structure of “harder”. Through extensive trials, a viscosity coefficient of 0.0005 was found to be helpful with convergence.

• (3) In cases of computation time being more critical than accuracy (Jiang 2005), the force and displacement convergence criteria were adjusted to reduce the computation time.

5 Validation of FE Model

5.1 Force–Displacement Relationships

The failure load for the numerical analysis was defined as peak load in the force –displacement relationship. Table 3 lists the failure loads and corresponding midspan displacements of the experimental work and the numerical analysis. The error of analysis was within 7 %. The difference in results can be a consequence of underestimation of the concrete’s fracture energy. The error of analysis for midspan displacement ranged from 5 to 23 %.

Table 3 Failure loads and corresponding displacements.

Relatively large deviation between the analytical and experimental results was observed in panels ST-FRC, ECT-NC and CFRP-NC. This may be due to the fact that data of material concrete of these panels may be incorrect, such as concrete material parameters of panel CFRP-NC are much higher than others (Table 3), but its midspan displacement is significantly smaller. Panel ST-FRC and ECT-NC also have the same problem. So in this paper, on the basis of a large number of comparative analyses, these panels was analyzed again after adjusting the concrete material parameters, the results see Table 3 and Fig. 11.

Fig. 11

Experimental and numerical applied load—midspan displacement curves.

The error of the failure loads was within 6 % and the error of the midspan displacement was within 10 % with the adjusted concrete model.

5.2 Failure Modes

Figures 12 and 13 compare the damage observed during the experiments with the damage predicted in the simulations. In the experiments, testing was terminated when brittle failure (concrete crushing) occurred. Figure 12 shows that at the peak load, concrete crushing occurred at the top of the panel at midspan, and flexural cracking (maximum principal plastic strain) was observed at the bottom surface of the panel near midspan. Figure 13 illustrates of the calculated compressive strain distribution of the panels. As shown in this figure, the failure due to the concrete crushing could be well predicted with the analysis.

Fig. 12

Observed failure mode of test specimen (Panel ST-NC-SL shown).

Fig. 13

Calculated maximum principal plastic strain distribution (Panel ST-NC-SL shown).

6 Parametric Analysis

The influence of the concrete dilation angles, viscosity parameters, and prestressing effect on the analytical results was investigated through parametric analysis of panel ST-NC-SL.

6.1 Effect of Concrete Dilation Angle $\mathbf{\psi }$

The dilation angle of a material is a measurement of the expansion of volume occurring when the material is under shear (as illustrated in Fig. 14) (Zhao and Cai 2010). For a Mohr–Coulomb material like concrete, the value of dilation angle generally varies in between zero (non-associative flow rule) and the friction angle (associative flow rule). (Tuo 2008) recommended 30° for concrete material. However, in this paper, the analytical results with a value of 38 were the most closest to the experimental results.

Fig. 14

Dilation angle.

From Fig. 15 it can be seen, as the dilation angle increased, the displacement capacity and the failure load of the panel was significantly increased while the required number of iterations to obtain a converged results decreased.

Fig. 15

Effect of concrete dilation angle.

6.2 Effect of µ Viscosity Parameter

Material models exhibiting softening behavior and stiffness degradation often lead to severe convergence difficulties in implicit analysis programs, such as Abaqus/Standard. A common technique to overcome these convergence difficulties is the use of a visco-plastic regularization of the constitutive equations, which causes the consistent tangent stiffness of the softening material to become positive for sufficiently small time increments.

The lower value of the parameter would result in more accurate calculation and more computation time. The influence of the value of the viscosity parameter on the analytical results is shown in Fig. 16. As shown in this figure, with decreasing of the value of viscosity parameter, the displacement capacity and failure load increased and the required number of iterations to reach a converged solution increased. When the viscosity parameter was taken as 0.0005, the calculation results were close to the experimental results. On the premise of no apparent loss calculation accuracy and efficiency, proposals should be taken as far as possible to the lower value.

Fig. 16

Effect of viscosity parameter μ.

6.3 Effect of Prestressing Force

Figure 17 shows the influence of the prestressing effect. As shown in this figure, increasing the prestressing effect (from 60 to 140 %), resulted in increasing of the cracking load (from 37 to 69 KN and decreasing of displacement capacity.). However, the post-cracking stiffness and the peak load the panels was not sensitive to the prestress effect since the post-cracking curves was parallel to each other with varied prestressing forces.

Fig. 17

Prestressed effect (Panel ST-NC-SL shown).

7 Conclusions

In this paper, finite element analysis of PPC bridge deck panels was conducted using concrete damage plasticity model. Based on the validation of finite element model against experimental results and parametric study with varied values of dilation angle, viscosity parameter, and prestressing force, following conclusions can be made:

• (1) The concrete damage plasticity model in ABAQUS can predict the concrete crushing failure mode in PPC panels. The numerical error of the failure loads and mid-span displacement was within 6 % and 10 %, respectively.

• (2) It was feasible and accurate enough to simulate the prestressing effect by applying temperature load to prestressing strands or tendons.

• (3) Under tri-axial compression state in the case of this paper, the ratio of initial equibiaxial compressive yield stress to initial uniaxial compressive yield stress σ _bo /σ _co was taken as 1.76 and was shown accurate to predict the behavior of PPC panels.

• (4) Increasing prestressing effect resulted in increasing of, the cracking load and decreasing of displacement capacity of the PPC panels as shown in the parametric study in this paper.

• (5) Lower values of viscosity of parameter increased calculation accuracy and increased the calculation time.