Abstract
This article proposes two regularized iterative algorithms for solving variational inequality problems defined over a solution set of a variational inclusion problem, known as hierarchical variational inequality problems, in the setting of Hadamard manifolds. Instead of regularizing the variational inequality problem or an iterative method for solving it, we first regularize the considered variational inclusion problem, and then prove that the solution of the regularized problem converges to a solution of the hierarchical variational inequality problem. Using such a result, we prove the convergence of the sequences generated by the proposed algorithms to a solution of the considered hierarchical variational inequality problem. A computational experiment is provided to see the validity and effectiveness of the proposed algorithms.
Similar content being viewed by others
1 Introduction
Over the past two decades, many problems from nonlinear analysis such as, fixed point problems, variational inequality problems, optimization problems, etc., have been extended from linear spaces to manifold settings, see, [1,2,3,4,5,6,7,8, 11, 13, 15,16,17,18, 20, 21, 26, 28, 29] and the references therein.
Let C be a nonempty closed and geodesic convex subset of a Hadamard manifold \({\mathbb {M}}\) and \(B:C\rightarrow T{\mathbb {M}}\) be a single-valued vector field. The variational inequality problem (in short, VIP) on a Hadamard manifold \({\mathbb {M}}\) was first studied by Németh [21], and is defined as follows:
where \(\exp _{\cdot }^{-1}\) is the inverse of the exponential map, and \(\langle .,. \rangle \) denotes the inner product on a tangent space in \({\mathbb {M}}\).
Very recently, Chen et al. [9] proposed two Tseng’s type extragradient iterative algorithms for finding the solution of VIP (1).
In 2009, Li et al. [16] first studied the variational inclusion problem for a set-valued vector field on a Hadamard manifold \({\mathbb {M}}\) which is defined as follows:
where \(A : {\mathbb {M}} \rightrightarrows T{\mathbb {M}}\) is a set-valued vector field on \({\mathbb {M}}\) and 0 denotes the zero tangent vector of the tangent space \(T_{x}{\mathbb {M}}\). They proposed the proximal point algorithm for the inclusion problem (2) and studied the convergence of the sequence generated by the proposed algorithm to a solution of the problem (2) under some suitable conditions. In [6], we discussed the regularized methods for proximal point algorithms for finding the solutions of the problem (2) when A is a maximal monotone set-valued vector field.
Later, we [3, 4] studied the following variational inclusion problem on a Hadamard manifold \({\mathbb {M}}\):
We denote by \(\mathbb {S}\) the solution set of the inclusion problem (3), and throughout this article, we assume that \(\mathbb {S} \ne \emptyset \). We [4] extended the proximal point algorithm of Li et al. [16] for the problem (3) and proved the convergence of the sequence generated by the proposed algorithm to a solution of the inclusion problem (3) under the maximal monotonicity of A and strong monotonicity and Lipschitz continuity of B with some other conditions on the parameter.
Very recently, Khammahawong et al. [14] presented two Tseng’s type iterative algorithms for solving the inclusion problem (3), where stepsizes in one algorithm are required by utilizing a line search, and in other algorithm, they are obtained by simple updating.
Very recently, Hieu et al. [12] considered a variational inequality problem which is defined over the set of solutions of a variational inclusion problem (3) in the setting of Hilbert spaces. Instead of regularizing the variational inequality problem, they regularized variational inclusion problem over which a variational inequality problem is defined. Then, they proposed three iterative regularization methods for solving such a problem.
Motivated and inspired by the work of Hieu et al. [12, 14], we consider the following variational inequality problem which is defined over the set of solutions of the variational inclusion problem (3) in the setting of a Hadamard manifold \({\mathbb {M}}\):
Such a problem is known as hierarchical variational inequality problem (in short, HVIP). As in [12], we first regularize variational inclusion problem (3), and then propose two Tseng’s type iterative methods for solving hierarchical variational inequality problem (4).
The organization of this article is as follows. In Sect. 2, we recall some definitions and results from manifolds. In Sect. 3, we discuss the regularization of the variational inclusion problem (3) and prove that a solution of the regularized variational inclusion problem converges to a solution of the hierarchical variation inequality problem (4). In Sect. 4, we propose two Tseng’s type iterative methods for finding the solution of the hierarchical variational inclusion problem (4) in the setting of Hadamard manifolds. The convergence analysis of proposed algorithms is also studied. In the last section, we demonstrate proposed algorithms by a numerical example.
2 Basic tools from manifolds and some preliminaries
Let \(T_{x} {\mathbb {M}}\) be the tangent space at the point x in a finite dimensional differentiable manifold \({\mathbb {M}}\). The collection of all such tangent spaces on \({\mathbb {M}}\) is called tangent bundle and it is denoted by \(T{\mathbb {M}}\). Since a tangent space is a real vector space of the same dimension as \({\mathbb {M}}\), an inner product \(\langle \cdot , \cdot \rangle _{x} : T_{x}{\mathbb {M}} \times T_{x}{\mathbb {M}} \rightarrow {\mathbb {R}}\), for all \(x\in {\mathbb {M}}\), can be defined on \(T_{x}{\mathbb {M}}\). The corresponding norm to the inner product \(\langle \cdot , \cdot \rangle _{x}\) on \(T_{x}{\mathbb {M}}\) is denoted by \(\Vert \cdot \Vert _{x}\). If there is no confusion, then we omit the subscript x. \(\langle \cdot , \cdot \rangle : T{\mathbb {M}} \times T{\mathbb {M}} \rightarrow {\mathbb {R}}\) \({\mathbb {M}}\). A differentiable manifold \({\mathbb {M}}\) endowed with a Riemannian metric \(\langle \cdot , \cdot \rangle \) is said to be a Riemannian manifold. The length of a piecewise smooth curve \(\gamma : [a, b] \rightarrow {\mathbb {M}}\) joining \(x = \gamma (a)\) to \(y=\gamma (b)\) in \({\mathbb {M}}\) is given by
where \({\dot{\gamma }}(t)\) denotes the tangent vector at \(\gamma (t)\) in the tangent space \(T_{\gamma (t)}{\mathbb {M}}\). The minimal length of all such curves joining x to y is known as the Riemannian distance and it is denoted by d(x, y).
Let \(\nabla \) be a Levi-Civita connection associated with the Riemannian manifold \({\mathbb {M}}\). For a smooth curve \(\gamma \), a tangent vector \({\dot{\gamma }}(t)\) along the curve \(\gamma \) is said to be parallel if \(\nabla _{{\dot{\gamma }}(t)}{\dot{\gamma }}(t) = \mathbf{0}\) for all \(t\in [a,b]\), where \(\mathbf{0}\) denotes the zero tangent vector; in this case, \(\gamma \) is called a geodesic and \(\Vert {\dot{\gamma }}(t)\Vert \) is a constant for all \(t \in [a,b]\). Moreover, if \(\Vert {\dot{\gamma }}(t)\Vert = 1\) for all \(t \in [a,b]\), then \(\gamma \) is called normalized geodesic. If the length of a geodesic joining x to y in the Riemannian manifold \({\mathbb {M}}\) equals d(x, y), then \(\gamma \) is said to be a minimal geodesic. If for any x in a Riemannian manifold \({\mathbb {M}}\), all geodesics emanating from x are defined for all \(t\in {\mathbb {R}}\), then the Riemannian manifold \({\mathbb {M}}\) is said to be (geodesically) complete. For a complete Riemannian manifold \({\mathbb {M}}\), the exponential map \(\exp _{x} : T_{x}{\mathbb {M}} \rightarrow {\mathbb {M}}\) at \(x\in {\mathbb {M}}\) is defined by
where \(\gamma _{u}(\cdot ; x)\) is the geodesic starting from x with velocity u, i.e., \(\gamma _{u}(0; x) = x\) and \({\dot{\gamma }}_{u}(0; x) = u\). It is known that \(\exp _{x} t u = \gamma _{u}(t; x)\) for any real number t, and \(\exp _{x} \mathbf{\mathbf{0}} =\gamma _{u}(0; x) = x\). It is also well known that the exponential map \(\exp _{x}\) is differentiable on \(T_{x}{\mathbb {M}}\) for any \(x\in {\mathbb {M}}\). The derivative \(\mathrm{D}\exp _{x}(\mathbf{\mathbf{0}})\) of \(\exp _{x}(\mathbf{\mathbf{0}})\) is equal to the identity vector of \(T_{x}{\mathbb {M}}\). Therefore, by the inverse mapping theorem, there exists an inverse exponential map \(\exp _{x}^{-1} : {\mathbb {M}} \rightarrow T_{x}{\mathbb {M}}\). For any \(x, y \in {\mathbb {M}}\), we have \(d(x, y) = \Vert \exp _{x}^{-1}y\Vert \). For further details, we refer [25].
The parallel transport \(P_{\gamma ,\gamma (b),\gamma (a)}:T_{\gamma (a)}{\mathbb {M}}\rightarrow T_{\gamma (b)}{\mathbb {M}}\) on the tangent bundle \(T{\mathbb {M}}\) along \(\gamma : [a,b] \rightarrow {\mathbb {M}}\) with respect to \(\nabla \) is defined as
where V is a unique vector field such that \(\nabla _{{\dot{\gamma }}(t)}V={{\textbf {0}}}\) for all \(t \in [a,b]\), and \(V(\gamma (a)) = v\). When \(\gamma \) is a minimal geodesic joining x to y, we write \(P_{y,x}\) instead of \(P_{\gamma ,y,x}\). For every \(a,b,c \in {\mathbb {R}}\), we have
\(P_{\gamma (b),\gamma (a)}\) is an isometry from \(T_{\gamma (a)}{\mathbb {M}}\) to \(T_{\gamma (b)}{\mathbb {M}}\), that is, the parallel transport preserve the inner product,
Theorem 2.1
[10, Hopf-Rinow Theorem] Let x be any point in a Riemannian manifold \({\mathbb {M}}\). Then the following assertions are equivalent:
-
(a)
The exponential mapping \(\exp _{x}\) is defined on \(T_{x}{\mathbb {M}}\).
-
(b)
The closed and bounded subsets of \({\mathbb {M}}\) are compact.
-
(c)
\({\mathbb {M}}\) is complete as a metric space.
-
(d)
\({\mathbb {M}}\) is geodesically complete.
Moreover, any of the equivalent statements (a)–(d) implies that
-
(e)
any \(x, y\in {\mathbb {M}}\) can be joined by a minimal geodesic whose arc length is equal to d(x, y).
A complete simply connected Riemannian manifold of nonpositive sectional curvature is said to be a Hadamard manifold.
Rest of the paper, unless otherwise specified, we assume that \({\mathbb {M}}\) is a finite-dimensional Hadamard manifold.
Recall the following properties of the exponential map.
Proposition 2.2
[25] The exponential map \(\exp _{x} : T_{x}{\mathbb {M}} \rightarrow {\mathbb {M}}\) is a diffeomorphism for all \(x \in {\mathbb {M}}\). For any two points \(x, y \in {\mathbb {M}}\), there exists a unique normalized geodesic \(\gamma : [0, 1] \rightarrow {\mathbb {M}}\) joining \(x = \gamma (0)\) to \(y = \gamma (1)\) which is in fact a minimal geodesic defined by
Lemma 2.3
[16] Let \(\{x_{n}\}_{n=0}^{\infty }\) be a sequence in a Hadamard manifold \({\mathbb {M}}\) such that \(x_{n} \rightarrow {\tilde{x}} \in {\mathbb {M}}\). Then the following assertions hold.
-
(a)
For every \(y \in {\mathbb {M}}\), we have
$$\begin{aligned} \exp _{x_{n}}^{-1}y \rightarrow \exp _{{\tilde{x}}}^{-1}y \quad \text{ and } \quad \exp _{y}^{-1}x_{n} \rightarrow \exp _{y}^{-1} {\tilde{x}}; \end{aligned}$$ -
(b)
If \(v_{n} \in T_{x_{n}}{\mathbb {M}}\) and \(v_{n} \rightarrow {\tilde{v}}\), then \({\tilde{v}} \in T_{{\tilde{x}}}{\mathbb {M}};\)
-
(c)
Given \(u_{n}, v_{n} \in T_{x_{n}}{\mathbb {M}}\) and \({\tilde{u}}, {\tilde{v}} \in T_{x_{0}}{\mathbb {M}}\), then
$$\begin{aligned} u_{n} \rightarrow {\tilde{u}} \text{ and } v_{n} \rightarrow {\tilde{v}} ~\Rightarrow ~ \langle u_{n}, v_{n} \rangle \rightarrow \langle {\tilde{u}}, {\tilde{v}} \rangle . \end{aligned}$$
A subset C of a Riemannian manifold \({\mathbb {M}}\) is said to be geodesic convex if for all \(x,y\in C\) and for any geodesic \(\gamma : [a, b] \rightarrow {\mathbb {M}}\), \(a, b \in {\mathbb {R}}\), such that \(x = \gamma (a)\) and \(y = \gamma (b)\), we have
A function \(f : {\mathbb {M}} \rightarrow {\mathbb {R}}\) is said to be geodesic convex if for any geodesic \(\gamma : [a, b]\rightarrow {\mathbb {M}}\), the composition function \(f \circ \gamma : [a, b]\rightarrow {\mathbb {R}}\) is convex, that is,
Moreover, \(f : {\mathbb {M}} \rightarrow {\mathbb {R}}\) is said to be strongly geodesic convex with constant \(\sigma >0\) if for any geodesic \(\gamma : [a, b]\rightarrow {\mathbb {M}}\), the composition function \(f \circ \gamma : [a, b]\rightarrow {\mathbb {R}}\) is strongly convex with constant \(\sigma \Vert {\dot{\gamma }}(0)\Vert ^2\), that is,
Proposition 2.4
[25] If \({\mathbb {M}}\) is a Riemannian manifold, then the Riemannian distance \(d : {\mathbb {M}} \times {\mathbb {M}}\rightarrow {\mathbb {R}}\) is a geodesic convex function with respect to the product Riemannian metric, i.e., for any pair of geodesics \(\gamma _{1} : [0,1] \rightarrow {\mathbb {M}}\) and \(\gamma _{2}: [0,1] \rightarrow {\mathbb {M}}\),
In particular, for any \(x \in {\mathbb {M}}\), the function \(d(\cdot , x): {\mathbb {M}} \rightarrow {\mathbb {R}}\) is a geodesic convex function.
A geodesic triangle \(\Delta (x_{1}, x_{2}, x_{3})\) in a Riemannian manifold \({\mathbb {M}}\) is a set which consists of three points \(x_{1}, x_{2}\) and \(x_{3}\), and three minimal geodesics \(\gamma _{i}\) joining \(x_{i}\) to \(x_{i+1}\), where \(i = 1, 2, 3 \pmod 3\).
Lemma 2.5
[17] Let \(\Delta (x_{1}, x_{2}, x_{3})\) be a geodesic triangle in a Hadamard manifold \({\mathbb {M}}\). Then, there exists \({{\tilde{x}}}_{1}, {{\tilde{x}}}_{2}, {{\tilde{x}}}_{3}\in {\mathbb {R}}^2\) such that
The triangle \(\Delta ({{\tilde{x}}}_{1}, {{\tilde{x}}}_{2}, {{\tilde{x}}}_{3})\) is called the comparison triangle of the geodesic triangle \(\Delta (x_{1}, x_{2}, x_{3})\), which is unique up to the isometry of \({\mathbb {R}}^{2}\). The points \({{\tilde{x}}}_{1}, {{\tilde{x}}}_{2}, \tilde{x}_{3}\) are called the comparison points to the points \(x_{1}, x_{2}, x_{3}\), respectively.
Proposition 2.6
[25] Let \(\Delta (x_{1}, x_{2}, x_{3})\) be a geodesic triangle in a Hadamard manifold \({\mathbb {M}}\). For each \(i = 1,2,3 \pmod 3\), let \(\gamma _{i} : [0, l_{i}] \rightarrow {\mathbb {M}}\) denote the geodesic joining \(x_{i}\) to \(x_{i+1}\), \(l_{i} = {\mathscr {L}}(\gamma _{i})\), and \(\theta _{i}\) be the angle between tangent vectors \({\dot{\gamma }}_{i}(0)\) and \({\dot{\gamma }}_{i-1}(l_{i-1})\). Then,
-
(a)
\(\theta _{1} + \theta _{2} + \theta _{3} \le \pi \);
-
(b)
\(l_{i}^{2} + l_{i+1}^{2} - 2l_{i}l_{i+1}\cos \theta _{i+1} \le l_{i-1}^{2}\).
As in [16], Proposition 2.6 (b) can be re-written in terms of Riemannian distance and exponential map as
since
For further detail, we refer [11].
Remark 2.7
[16] For every \(x,y\in {\mathbb {M}}\) and \(v\in T_{x}{\mathbb {M}},\) we have
Remark 2.8
Let \(x,y,z\in {\mathbb {M}}\) and \(v\in T_{x}{\mathbb {M}}.\) By using (6) and Remark 2.7, we have
We close this section by recalling some properties and results related to the sequences of real numbers.
Remark 2.9
For any sequences \(\{\alpha _{n}\}\) and \(\{\beta _{n}\}\) of real numbers, using arithmetic mean and geometric mean inequality, we have
Lemma 2.10
[30] Let \(\{a_{n}\}\) be a sequence of nonnegative real numbers such that
where \(\{\zeta _{n}\}\subseteq (0,1)\) and \(\{\delta _{n}\}\) are sequences of real numbers such that the following conditions hold:
-
(a)
\(\lim \nolimits _{n\rightarrow \infty }\zeta _{n}=0;\)
-
(b)
\(\sum \nolimits _{n=0}^{\infty }\zeta _{n}=+\infty ;\)
-
(c)
\(\limsup \nolimits _{n\rightarrow \infty }\frac{\delta _{n}}{\zeta _{n}}\le 0\).
Then, \(\lim \nolimits _{n\rightarrow \infty }a_{n}=0.\)
3 Regularized variational inclusion problems
A single-valued vector field on \({\mathbb {M}}\) is a single-valued mapping \(B :{\mathbb {M}}\rightarrow T{\mathbb {M}}\) that assigns a tangent vector \(B(x) \in T_{x}{\mathbb {M}}\) for all \(x \in {\mathbb {M}}\). The set of all such single-valued vector fields is denoted by \(\Omega ({\mathbb {M}})\). A set-valued vector field A on \({\mathbb {M}}\) is a set-valued mapping \(A:{\mathbb {M}}\rightrightarrows T{\mathbb {M}}\) that assigns a subset A(x) of \(T_{x}{\mathbb {M}}\) for all \(x\in {\mathbb {M}}\). The collection of all such set-valued vector fields is denoted by \({\mathscr {X}}({\mathbb {M}})\). The domain of a set-valued vector field \(A : {\mathbb {M}}\rightrightarrows T{\mathbb {M}}\) is defined by \(\mathrm{D}(A) = \{x \in {\mathbb {M}} : A(x) \ne \emptyset \}.\)
Definition 3.1
[20, 29] A single-valued vector field \(B\in \Omega ({\mathbb {M}})\) is said to be
-
(a)
monotone if for every \(x, y\in {\mathbb {M}}\),
$$\begin{aligned} \left\langle B(x), \exp ^{-1}_{x}y \right\rangle \le \left\langle B(y), -\exp ^{-1}_{y}x \right\rangle ; \end{aligned}$$ -
(b)
strongly monotone if there is a constant \(\sigma >0\) such that for every \(x, y \in {\mathbb {M}}\),
$$\begin{aligned} \left\langle B(x), \exp ^{-1}_{x}y \right\rangle + \left\langle B(y), \exp ^{-1}_{y}x \right\rangle \le -\sigma d^{2}(x, y); \end{aligned}$$ -
(c)
L-Lipschitz continuous if there exists a constant \(\mathrm L > 0\) such that for every \(x, y \in {\mathbb {M}}\),
$$\begin{aligned} \Vert P_{x,y}B(y)-B(x)\Vert \le \text{ L }~d(x,y); \end{aligned}$$ -
(d)
maximal monotone if it is monotone and for every \(x,y\in {\mathbb {M}}\) and \(u \in T_{x}{\mathbb {M}}\), the condition
$$\begin{aligned} \left\langle u, \exp ^{-1}_{x}y \right\rangle \le \left\langle B(y), -\exp ^{-1}_{y}x \right\rangle , \end{aligned}$$implies \(u=B(x).\)
Definition 3.2
[16, 22] A set-valued vector field \(A\in {\mathscr {X}}({\mathbb {M}})\) is said to be
-
(a)
monotone if for every \(x, y \in \mathrm{D}(A)\),
$$\begin{aligned} \left\langle u, \exp ^{-1}_{x}y \right\rangle \le \left\langle v, -\exp ^{-1}_{y}x \right\rangle , \quad \forall u\in A(x) \text{ and } \forall v\in A(y); \end{aligned}$$ -
(b)
strongly monotone if there is a constant \(\sigma >0\) such that for every \(x, y \in \mathrm{D}(A)\),
$$\begin{aligned} \left\langle u, \exp ^{-1}_{x}y \right\rangle + \left\langle v, \exp ^{-1}_{y}x \right\rangle \le -\sigma d^{2}(x, y), \quad \forall u\in A(x) \text{ and } \forall v\in A(y); \end{aligned}$$ -
(c)
maximal monotone if it is monotone and for all \(x \in \mathrm{D}(A)\) and \(u \in T_{x}{\mathbb {M}}\), the condition
$$\begin{aligned} \left\langle u, \exp ^{-1}_{x}y \right\rangle \le \left\langle v, -\exp ^{-1}_{y}x \right\rangle , \quad \forall y \in \mathrm{D}(A) \text{ and } \forall v \in A(y), \end{aligned}$$implies \(u \in A(x)\);
-
(d)
upper Kuratowski semicontinuous at \(x \in \mathrm{D}(A)\) if for every sequences \(\{x_{n}\}_{n=0}^{\infty }\subseteq \mathrm{D}(A)\) and \(\{u_{n}\}_{n=0}^{\infty }\subset T{\mathbb {M}}\) with \(u_{n}\in A(x_{n})\), the relations \(\lim \limits _{n\rightarrow \infty }u_{n}=u\) and \(\lim \limits _{n\rightarrow \infty }x_{n}=x\) imply \(u\in A(x)\).
Furthermore, A is said to be upper Kuratowski semicontinuous on \({\mathbb {M}}\) if it is upper Kuratowski semicontinuous at each \(x\in \mathrm{D(A)}\).
Remark 3.3
-
(a)
It can be easily seen that if \(A\in {\mathscr {X}}({\mathbb {M}})\) is a set-valued monotone vector field and \(B\in \Omega ({\mathbb {M}})\) is a single-valued monotone vector field, then \(A+B\) is a set-valued monotone vector field.
-
(b)
If \(A, B \in {\mathscr {X}}({\mathbb {M}})\) are set-valued maximal monotone vector fields such that \(\mathrm {D}(A)\cap \text{ int }~\mathrm {D}(B) \ne \emptyset \), where int \(\mathrm {D}(B)\) denotes the interior of \(\mathrm {D}(B)\), then \(A+B\) is a set-valued maximal monotone vector field (see [24]).
Lemma 3.4
[16] Every maximal monotone set-valued vector field \(A\in {\mathscr {X}}({\mathbb {M}})\) is upper Kuratowski semicontinuous on \({\mathbb {M}}\).
Theorem 3.5
[16] Let \(A\in {\mathscr {X}}({\mathbb {M}})\) be a maximal and strongly monotone vector field with \(\mathrm {D}(A) = {\mathbb {M}}\). Then, there exists a unique \({\bar{x}}\in {\mathbb {M}}\) such that \(\mathbf{0}\in A({\bar{x}})\).
Definition 3.6
[15, 17] Let C be a nonempty subset of a Hadamard manifold \({\mathbb {M}}\). A mapping \(T: C \rightarrow {\mathbb {M}}\) is said to be
-
(a)
nonexpansive if
$$\begin{aligned} d(T(x),T(y))\le d(x,y), \quad \forall x,y \in C; \end{aligned}$$ -
(b)
firmly nonexpansive if for every \(x,y\in C\), the function \(\phi : [0,1] \rightarrow [0,\infty ]\) defined by
$$\begin{aligned} \phi (t):=d\left( \exp _{x}t\exp ^{-1}_{x}T(x), \exp _{y}t\exp ^{-1}_{y}T(y)\right) ,\quad \forall t\in [0,1], \end{aligned}$$is nondecreasing.
Remark 3.7
[15] Every firmly nonexpansive mapping is nonexpansive.
Definition 3.8
[21] Let C be a nonempty geodesic convex subset of a Hadamard manifold \({\mathbb {M}}\). A single-valued vector field \(F:C\rightarrow T{\mathbb {M}}\) is said to be geodesic hemicontinuous if for every geodesic \(\gamma :[0,1]\rightarrow C\) and \(u\in T_{\gamma (0)}{\mathbb {M}}\), the function \(t\mapsto \left\langle P_{\gamma (0),\gamma (t)}F(\gamma (t)),u \right\rangle \) is continuous.
Definition 3.9
[15] For a given \(\lambda >0\) and a set-valued vector field \(A\in {\mathscr {X}}({\mathbb {M}})\), the resolvent related to A of order \(\lambda \) is a set-valued mapping \(J^{A}_{\lambda }:{\mathbb {M}}\rightrightarrows \mathrm D(A)\) defined by
Theorem 3.10
[15] Let \(A\in {\mathscr {X}}({\mathbb {M}})\) be a set-valued vector field. Then the following assertions hold for all \(\lambda >0,\)
-
(a)
The vector field A is monotone if and only if \(J^{A}_{\lambda }\) is single-valued and firmly nonexpansive;
-
(b)
Let \(\mathrm {D}(A)={\mathbb {M}}\). The vector field A is maximal monotone if and only if \(J^{A}_{\lambda }\) is single-valued, firmly nonexpansive and \(\mathrm {D}(J^{A}_{\lambda })={\mathbb {M}}\).
Remark 3.11
-
(a)
It can be easily seen that the set \(\text{ Fix }(T)\) of fixed points of a nonexpansive mapping \(T : C \rightarrow {\mathbb {M}}\) defined on a Hadamard manifold \({\mathbb {M}}\) is closed and geodesic convex; See, for example, [1].
-
(b)
If \(A\in {\mathscr {X}}({\mathbb {M}})\) and \(B\in \Omega ({\mathbb {M}})\) are monotone vector fields, then so is \(A+B\in {\mathscr {X}}({\mathbb {M}})\). Therefore, in view of Theorem 3.10 (a), we see that \(J^{A+B}_{\lambda }\) is nonexpansive, and \(\text{ Fix }(J^{A+B}_{\lambda })=(A+B)^{-1}(\mathbf{0})\) for each \(\lambda >0\) (see [15]). Indeed,
$$\begin{aligned} x\in \text{ Fix }(J^{A+B}_{\lambda }) \Leftrightarrow x\in J^{A+B}_{\lambda }(x) \Leftrightarrow x \in \exp _{x} \lambda (A+B)(x) \Leftrightarrow \mathbf{0}\in (A+B)(x). \end{aligned}$$Hence,
 is closed and geodesic convex.
is closed and geodesic convex. -
(c)
In view of [21, Theorem 1] and the above remark, if \(F\in \Omega ({\mathbb {M}})\) is a strongly monotone and Lipschitz continuous vector field, then the problem (4) has a unique solution.
Lemma 3.12
Let \(B\in \Omega ({\mathbb {M}})\) be a monotone and geodesic hemicontinuous single-valued vector field with \(\mathrm{D}(B) = {\mathbb {M}}\). Then B is maximal monotone.
Proof
Let \(x\in {\mathbb {M}}\) and \(u\in T_{x}{\mathbb {M}}\) be such that
equivalently,
Consider the geodesic \(\gamma (t)=\exp _{x}t\exp ^{-1}_{x}y\) for \(t\in (0,1)\), then
Letting \(t\rightarrow 0\) and using geodesic hemicontinuity of B, we get
In particular, take \(y=\exp _{x}(u-B(x))\) in (8), we get \(u=B(x)\). Hence, B is maximal monotone vector field.
\(\square \)
Proposition 3.13
Let \(A\in {\mathscr {X}}({\mathbb {M}})\) be a maximal monotone set-valued vector field and \(B\in \Omega ({\mathbb {M}})\) be a monotone and geodesic hemicontinuous single-valued vector field with \(\mathrm {D}(B) = {\mathbb {M}}\). Then, \(A+B\) is a maximal monotone set-valued vector field.
Proof
Since B is a monotone and geodesic hemicontinuous single-valued vector field with \(\mathrm {D}(B) = {\mathbb {M}}\), by Lemma 3.12, B is a maximal monotone vector field. Hence, by Remark 3.3 (b), we get the conclusion. \(\square \)
To propose regularization iterative methods for computing the approximate solutions of the HVIP (4), we consider the following regularized variational inclusion problem.
Let \(A\in {\mathscr {X}}({\mathbb {M}})\) be a set-valued vector field and \(B,F\in \Omega ({\mathbb {M}})\) be single-valued vector fields. For each \(\alpha >0\), the following regularized variational inclusion problem (in short, RVIP) is to find \({\bar{x}} \in {\mathbb {M}}\) such that
If \(A\in {\mathscr {X}}({\mathbb {M}})\) is a maximal monotone set-valued vector field and \(B\in \Omega ({\mathbb {M}})\) is a monotone and geodesic hemicontinuous single-valued vector field, with \(\text{ D }(B) = {\mathbb {M}}\), then by Proposition 3.13, \(A+B\) is maximal monotone. If \(F\in \Omega ({\mathbb {M}})\) is a strongly monotone and geodesic hemicontinuous single-valued vector field, so is \(\alpha F\) for each \(\alpha > 0\). Therefore, if \(\mathrm {D}(A) = \mathrm{D}(B) = \mathrm{D}(F) = {\mathbb {M}}\), then by Theorem 3.5, for each \(\alpha >0\), RVIP (9) has a unique solution. We denote such a unique solution by \(x_{\alpha }\), that is,
Lemma 3.14
Let \(A\in {\mathscr {X}}({\mathbb {M}})\) be a monotone set-valued vector field, \(B\in \Omega ({\mathbb {M}})\) be a monotone single-valued vector field, and \(F\in \Omega ({\mathbb {M}})\) be a \(\sigma \)-strongly monotone single-valued vector field. If for each \(\alpha >0\), \(x_{\alpha }\) is a solution of RVIP (9), then \(\{x_{\alpha }\}\) is bounded. In fact, for any (fixed) \(x^{*}\in \mathbb {S} := \{ x \in {\mathbb {M}} : x \in (A+B)^{-1}({\mathbf{0}}) \}\),
Proof
Since for each \(\alpha >0\), \(x_{\alpha }\) is a solution of RVIP (9), we have \(-\alpha F(x_{\alpha })\in (A+B)(x_{\alpha })\). Let \(x^{*}\in \mathbb {S}\), that is, \(\mathbf{{0}}\in (A+B)(x^{*})\). By the monotonicity of \(A+B\), we have
that is, \(\left\langle F(x_{\alpha }),\exp ^{-1}_{x_{\alpha }}x^{*} \right\rangle \ge 0.\) By the \(\sigma \)-strong monotonicity of F, we have
that is,
By Cauchy–Schwarz inequality, we obtain
and therefore,
Thus, \(\{x_{\alpha }\}\) is bounded. \(\square \)
Lemma 3.15
Let \(A\in {\mathscr {X}}({\mathbb {M}})\) be a monotone set-valued vector field, \(B\in \Omega ({\mathbb {M}})\) be a monotone single-valued vector field, and \(F\in \Omega ({\mathbb {M}})\) be a \(\sigma \)-strongly monotone and Lipschitz continuous single-valued vector field. If for \(\alpha >0\) and \(\beta >0\), \(x_{\alpha }\) and \(x_{\beta }\) are the solutions of RVIP (9), then there exists \(\mu >0\) such that
Proof
Since \(x_{\alpha }\) and \(x_{\beta }\) are solutions of RVIP (9) for \(\alpha >0\) and \(\beta >0\), respectively, we have
By the monotonicity of \(A+B\), we have
that is,
By adding \(\alpha \left\langle F(x_{\beta }),-\exp ^{-1}_{x_{\beta }} x_{\alpha }\right\rangle \), we obtain
or
Then, by \(\sigma \)-strongly monotonicity of F and Cauchy–Schwarz inequality, we obtain
Hence,
Since F is Lipschitz continuous and \(\{x_{\beta }\}\) is bounded, therefore \(\{F(x_{\beta })\}\) is also bounded. Thus, there exists \(\mu >0\) such that \(\frac{\Vert F(x_{\beta })\Vert }{\sigma } \le \mu \) for all \(\beta >0\). This together with inequality (12) implies the required conclusion.
\(\square \)
Lemma 3.16
Let \(A\in {\mathscr {X}}({\mathbb {M}})\) be a monotone and upper Kuratowski semicontinuous set-valued vector field, \(B\in \Omega ({\mathbb {M}})\) be a monotone and continuous single-valued vector field, and \(F\in \Omega ({\mathbb {M}})\) be a \(\sigma \)-strongly monotone and Lipschitz continuous single-valued vector field. If for each \(\alpha >0\), \(x_{\alpha }\) is a solution of RVIP (9), then \(\lim \limits _{\alpha \rightarrow 0}x_{\alpha }={\bar{x}}\), where \({\bar{x}}\) is a solution of HVIP (4).
Proof
By Lemma 3.14, \(\{x_{\alpha }\}\) is bounded, and so without loss of generality, we may assume a sequence \(\{\alpha _{n}\}\) in (0,\(\infty \)) with \(\alpha _{n}\rightarrow 0\) as \(n\rightarrow \infty \) such that the sequence \(\{x_{\alpha _{n}}\}\) of \(\{x_{\alpha }\}\) converges to a cluster point \({\bar{x}}\) of \(\{x_{\alpha }\}\). Since \(x_{\alpha _{n}}\) is a solution of the problem RVIP (9), we have
Since F is Lipschitz continuous and \(\{x_{\alpha _{n}}\}\) is bounded, so is \(\{F(x_{\alpha _{n}})\}\), and therefore, we have \(\lim \limits _{n\rightarrow \infty }\Vert \alpha _{n}F(x_{\alpha _{n}})\Vert =\lim \limits _{n\rightarrow \infty }|\alpha _{n}|\Vert F(x_{\alpha _{n}})\Vert =0\), that is,
Since B is continuous and \(x_{\alpha _{n}} \rightarrow {\bar{x}}\) as \(n\rightarrow \infty \), we have \(B(x_{\alpha _{n}})\rightarrow B({\bar{x}})\) as \(n\rightarrow \infty \). By combining (13) and (14), we have \(z_{\alpha _{n}}\rightarrow -B({\bar{x}})\) as \(n \rightarrow \infty \). Since A is upper Kuratowski semicontinuous, we obtain \(-B({\bar{x}})\in A({\bar{x}})\), that is, \({\bar{x}}\in (A+B)^{-1}(\mathbf{0})=\mathbb {S}\). Since (11) hold for any \(x^{*}\in \mathbb {S}\), so we can rewrite it as
and therefore, for \(\alpha =\alpha _n\), we get
Consequently,
Letting \(n\rightarrow \infty \) and using Lemma 2.3 (a), we obtain
By Remark 3.11 (b), \(\mathbb {S}\) is geodesic convex, and therefore, \(\gamma (t)=\exp _{{\bar{x}}}(t\exp ^{-1}_{{\bar{x}}}x)\in \mathbb {S}\) for all \(t\in (0,1)\) and all \(x\in \mathbb {S}\). Hence by (17), for all \(x\in \mathbb {S}\), we have
or
Let \(P_{\gamma (0),\gamma (t)}\) denote the parallel transport along the geodesic \(\gamma :[0,1]\rightarrow \mathbb {S}\) from \(\gamma (0)={\bar{x}}\) to \(\gamma (t)\). From Remark 2.7 and relation (18), we get
that is,
and thus,
Since F is Lipschitz continuous, by letting \(t\rightarrow 0\) in inequality (19), we obtain
Since \({\bar{x}}\) was arbitrary cluster point which solves problem (4), which is uniquely solvable. Therefore, \(x_{\alpha } \rightarrow {\bar{x}}\) as \(\alpha \rightarrow 0\). Hence, \(\lim \limits _{\alpha \rightarrow 0}x_{\alpha } = {\bar{x}}\), where \({\bar{x}}\) is a solution of (4). \(\square \)
4 Regularized iterative methods and convergence results
Consider the sequences \(\{\lambda _{n}\}\) and \(\{\alpha _{n}\}\) of positive real numbers and two real numbers \({\bar{\lambda }}\) and \({\underline{\lambda }}\) such that \(0<{\bar{\lambda }}\le {\underline{\lambda }}\). Assume that the following conditions hold:
-
(H1)
\(\{\lambda _{n}\}\subset [{\bar{\lambda }},{\underline{\lambda }}]\subset \left( 0,\frac{1}{L1}\right) ;\)
-
(H2)
\(\lim \limits _{n\rightarrow \infty }\alpha _{n}=0;\)
-
(H3)
\(\sum _{n=1}^{\infty } \alpha _{n}\lambda _{n}=+\infty ;\)
-
(H4)
\(\lim \limits _{n\rightarrow \infty }\frac{|\alpha _{n}-\alpha _{n+1}|}{\alpha _{n}^2}=0.\)

Remark 4.1
Algorithm 1 can be seen as an extension of Algorithm 2 in [12] from Hilbert space to Hadamard manifold settings.
To study the convergence of the sequence generated by Algorithm 1 to a solution of HVIP (4), we first establish the following lemma.
Lemma 4.2
Let \(A\in {\mathscr {X}}({\mathbb {M}})\) be a monotone set-valued vector field, \(B\in \Omega ({\mathbb {M}})\) be a monotone single-valued vector field, and \(F\in \Omega ({\mathbb {M}})\) be a single-valued vector fields Let \(\{x_{n}\}\) be a sequence generated by Algorithm 1 and \(\{x_{\alpha _{n}}\}\) be a sequence given by (10). Then,
Proof
Considering \(\alpha =\alpha _{n}\) in (10), we obtain
On the other hand, from (20), we have \(-P_{y_{n},x_{n}}B(x_{n})-\alpha _{n}P_{y_{n},x_{n}}F(x_{n})+\frac{1}{\lambda _{n}}\exp ^{-1}_{y_{n}}x_{n}\in A(y_{n}).\) Then, it follows from the monotonicity of A that
By the monotonicity of B, we have
which implies that
Since parallel transport is isometric and \(P_{x_{\alpha _{n}},y_{n}}\exp ^{-1}_{y_{n}}x_{\alpha _{n}}=-\exp ^{-1}_{x_{\alpha _{n}}}y_{n},\) we have
and therefore, inequality (24) becomes
equivalently,
From (21), we have
By combining (25) and (26), we get
Consider the geodesic triangle \(\Delta (x_{n},y_{n},x_{\alpha _{n}})\). Then by (6), we have
Consider another geodesic triangle \(\Delta (x_{n+1},x_{\alpha _{n}},y_{n})\). Then by (6), we have
From relation (26), we have
and therefore, the inequality (30) becomes
It follows from Remarks 2.7 and 2.8 that
By combining (32) and (33), we get
and thus, the inequality (34) becomes
By using (27), it reduces to (22). \(\square \)
Theorem 4.3
Let \(A\in {\mathscr {X}}({\mathbb {M}})\) be a maximal monotone set-valued vector field with \(\mathrm{D}(A)={\mathbb {M}}\), \(B\in \Omega ({\mathbb {M}})\) be a monotone and \(L_{1}\)-Lipschitz continuous single-valued vector field, and \(F\in \Omega ({\mathbb {M}})\) be a \(\sigma \)-strongly monotone and \(L_{2}\)-Lipschitz continuous single-valued vector field with \(\mathrm{D}(B) = \mathrm{D}(F) = {\mathbb {M}}\). Suppose that the conditions (H1)-(H4) hold. Then, the sequence \(\{x_n\}\) generated by Algorithm 1 converges to a solution \({\bar{x}}\) of HVIP (4).
Proof
As \(\sigma >0\), we can choose two numbers \(\epsilon _{1}>0\) and \(\epsilon _{2}>0\) such that
By Remark 2.8, we obtain
On the other hand, the \(\sigma \)-strongly monotonicity of F implies that
Therefore, the inequality (37) becomes
Since F is \(L_{2}\)-Lipschitz continuous, by Cauchy–Schwarz inequality, we get
From Remark 2.9, we have
By combining (38), (39) and (40), we get
From Lemma 4.2 and inequality (41), we obtain
The Lipschitz continuity of B implies that
Since \(\{\lambda _{n}\}\subset [{\bar{\lambda }},{\underline{\lambda }}]\subset \left( 0,\frac{1}{L1}\right) \) and \(\alpha _{n}\rightarrow 0,\) there exists \(n_{0}\ge 1\) such that
As \(\alpha _{n}\lambda _{n}\rightarrow 0\) as \(n\rightarrow \infty \), we have
and thus,
Therefore, using (44), (45) and (46), inequality (43) becomes
Consider the geodesic triangle \(\Delta (x_{n+1},x_{\alpha _{n}},x_{\alpha _{n+1}})\). Then by Lemma 2.5, there exists a comparison triangle \(\Delta (\tilde{x}_{n+1},{{\tilde{x}}}_{\alpha _{n}},{{\tilde{x}}}_{\alpha _{n+1}})\) such that
\(\qquad \qquad d(x_{\alpha _{n+1}},x_{n+1})=\Vert {{\tilde{x}}}_{\alpha _{n+1}}-{{\tilde{x}}}_{n+1}\Vert .\)
Note that
From Remark 2.9, we have
From (48) and (49), and Lemma 3.15, we obtain
This together with (47) implies that
Since \(1-\epsilon _{2}\alpha _n\lambda _{n}>0,~\forall n\ge n_{0},\) it gives that
Set \(a_n:=d(x_{n},x_{\alpha _{n}})\), \(\zeta _{n}:=\frac{(2\sigma -L_2\epsilon _{1}-\epsilon _{2})\alpha _{n}\lambda _{n}}{1-\epsilon _{2}\alpha _{n}\lambda _{n}}\), and \(\delta _{n}:=\frac{\mu ^2}{\epsilon _{2}\lambda _{n}}\frac{(\alpha _{n}-\alpha _{n+1})^2}{\alpha _{n}^3}\). Then the inequality (52) becomes
From (46), \(\zeta _{n}\in (0,1)\) for all \(n\ge n_{0}\). By the conditions (H1)-(H3), we conclude that \(\sum \limits _{n= n_{0}}^\infty \zeta _{n}=+\infty \), and the condition (H4) assures that
By (53) and Lemma 2.10, we get \(a_n=d^2(x_{n},x_{\alpha _{n}})\rightarrow 0\) as \(n\rightarrow \infty \). From Lemma 3.16, it immediately follows that \(x_{n}\rightarrow {\bar{x}}\) as \(n\rightarrow \infty \). \(\square \)
Algorithm 1 can be applied only when the Lipchitz constant \(L_{1}\) of B is known which is the drawback of Algorithm 1, because sometime either Lipschitz constant is unknown or difficult to find it. To avoid this disadvantage, we propose another method which can be easily implemented without the prior knowledge of Lipschitz constant \(L_{1}\) of the vector field B.

Remark 4.4
-
(a)
In Algorithm 2, the stepsizes increase iteration by iteration and so they reduce the dependence on the initial stepsize \(\lambda _{0}\). Since the sequence \(\{ q_{n} \}\) is summable, we obtain \(\displaystyle \lim _{n \rightarrow \infty } q_{n} = 0\). Therefore, the stepsizes may be nonincreasing when n is large. So, if F is a zero vector field, then Algorithm 2 is more general than the algorithm considered in [14] for solving variational inclusion problem (3) where stepsizes are considered to be decreasing.
-
(b)
Liu and Yang [19] used similar type of stepsizes to propose an iterative algorithm for solving variational inequality problem in the setting of Hilbert spaces.
We need the following lemma to establish the convergence of the sequences generated by Algorithm 2 to a solution of HVIP (4).
Lemma 4.5
If \(B\in \Omega ({\mathbb {M}})\) is a \(L_{1}\)-Lipschitz continuous single-valued vector field, then
-
(a)
the sequence \(\{\lambda _{n}\}\) generated by (55) is bounded,
-
(b)
\(\lim \limits _{n\rightarrow \infty }\lambda _{n}=\lambda \) and \(\lambda \in \left[ \min \left\{ \lambda _{0},\frac{\nu }{L_{1}}\right\} ,\lambda _{0}+Q\right] \), where \(Q=\sum \limits _{n=0}^{\infty }q_{n}\),
-
(c)
\(\Vert P_{y_{n},x_{n}}B(x_{n})-B(y_{n})\Vert \le \frac{\nu d(x_{n},y_{n})}{\lambda _{n+1}}\).
Proof
(a) From the definition of \(\lambda _{n}\), we have
that is,
Since B is \(L_{1}\)-Lipschitz continuous, we have
and therefore,
This together with (55) implies that
Hence, from (56) and (57), \(\{\lambda _{n}\}\) is bounded sequence.
(b) Let \((\lambda _{n+1}-\lambda _{n})_{+}=\max \{0,\lambda _{n+1}-\lambda _{n}\}\) and \((\lambda _{n+1}-\lambda _{n})_{-}=\max \{0,-(\lambda _{n+1}-\lambda _{n})\}\). By the definition of \(\lambda _{n}\), we have
Thus, the series \(\sum \limits _{n=0}^{\infty }(\lambda _{n+1}-\lambda _{n})_{+}\) is convergent.
Next we prove the convergence of the series \(\sum \limits _{n=0}^{\infty }(\lambda _{n+1}-\lambda _{n})_{-}\). Suppose that \(\sum \limits _{n=0}^{\infty }(\lambda _{n+1}-\lambda _{n})_{-}=+\infty .\) Note that
therefore, we get
Taking \(n\rightarrow +\infty \) in (60), we get \(\lim \limits _{n\rightarrow +\infty }\lambda _{n}=-\infty \). which is a contradiction. From the convergence of the series \(\sum \limits _{n=0}^{\infty }(\lambda _{n+1}-\lambda _{n})_{+}\) and \(\sum \limits _{n=0}^{\infty }(\lambda _{n+1}-\lambda _{n})_{-}\), and taking \(n\rightarrow \infty \) in (60), we get \(\lim \limits _{n\rightarrow \infty }\lambda _{n}=\lambda .\) Since \(\lambda _{n}\) has the lower bound \(\min \left\{ \frac{\nu }{L_{1}},\lambda _{0}\right\} \) and upper bound \(\lambda _{0}+Q\), we have \(\lambda \in \left[ \min \left\{ \lambda _{0},\frac{\nu }{L_{1}}\right\} ,\lambda _{0}+Q\right] \).
(c) Clearly, from (55), we have
Indeed, if \(P_{y_{n},x_{n}}B(x_{n})=B(y_{n})\), then (61) holds directly. Let \(P_{y_{n},x_{n}}B(x_{n})\ne B(y_{n})\), then it follows from (55) that
Thus,
Hence, (61) holds for \(P_{y_{n},x_{n}}B(x_{n})=B(y_{n})\) as well as for \(P_{y_{n},x_{n}}B(x_{n})\ne B(y_{n})\). \(\square \)
Theorem 4.6
Let \(A\in {\mathscr {X}}({\mathbb {M}})\) be a maximal monotone set-valued vector field with \(\mathrm{D}(A)={\mathbb {M}}\), \(B\in \Omega ({\mathbb {M}})\) be a monotone and \(L_{1}\)-Lipschitz continuous single-valued vector field, and \(F\in \Omega ({\mathbb {M}})\) be a \(\sigma \)-strongly monotone and \(L_{2}\)-Lipschitz continuous single-valued vector field with \(\mathrm{D}(B) = \mathrm{D}(F)={\mathbb {M}}\). Suppose that the conditions (H2)-(H4) hold. Then, the sequence \(\{x_n\}\) generated by Algorithm 2 converges to a solution \({\bar{x}}\) of HVIP (4).
Proof
From Lemma 4.2, we have
By Lemma 4.5 (c), it reduces to
Consider \(\epsilon _{1}>0\) and \(\epsilon _{2}>0\) such that (36) holds. Since \(\lambda _{n}\rightarrow \lambda \), \(\nu \in (0,1)\) and \(\alpha _{n}\rightarrow 0\), there exists \(k\in \mathbb {N}\) such that
and
By using relations (41) in (63), we obtain
and therefore,
It follows from (64) that
Remaining of the proof is similar to that of the proof of Theorem 4.3. \(\square \)
5 Computational experiment
Let \(f : {\mathbb {M}} \rightarrow {\mathbb {R}}\) be a differentiable function on \({\mathbb {M}}\). Then the gradient of f, denoted by \(\text{ grad }~f(x)\), at x [10] is defined by
where \(f'\) is a directional derivative of f at x in the direction \(w \in T_x{\mathbb {M}}\), defined by
The gradient of f on the Hadamard manifold \(({\mathbb {R}}_{++}^n,\left\langle ,\right\rangle )\) is given by
where \(G(x)^{-1}\) is inverse of the matrix G(x). Then, we have
where \(\min \limits _{x\in {\mathbb {M}}}f = \{x \in {\mathbb {M}} : f(x) \le f(y), \, \forall y\in {\mathbb {M}}\}\) is a set of minimizer of f over \({\mathbb {M}}\).
Proposition 5.1
[23] If \({\mathbb {M}}\) is a Riemannian manifold and \(f : {\mathbb {M}} \rightarrow {\mathbb {R}}\) be a differentiable function. Then,
-
(a)
f is geodesic convex if and only if \(\text{ grad }f\) is a monotone vector field;
-
(b)
f is strongly geodesic convex if and only if \(\text{ gard }f\) is a strongly monotone vector field.
If \(f : {\mathbb {M}} \rightarrow {\mathbb {R}}\) is a twice differentiable function, then the Hessian of f at \(x\in {\mathbb {M}}\) [27], denoted by \(\text {Hess} f\), is defined by
where \(\nabla _u\) is the Riemannian connection of \({\mathbb {M}}\).
Proposition 5.2
[8] Let \({\mathbb {M}}\) be a Hadamard manifold and \(f: {\mathbb {M}} \rightarrow {\mathbb {R}}\) be a twice continuously differentiable function. If \(\mathrm{Hess}\, f\) is bounded, then the gradient vector field \(\text{ grad }~f\) is Lipschitz continuous.
The subdifferential \(\partial f : {\mathbb {M}} \rightrightarrows T{\mathbb {M}}\) of f at x [25] is defined by
Lemma 5.3
[16] If \(f : {\mathbb {M}} \rightarrow {\mathbb {R}}\cup \{+\infty \}\) is a proper, lower semicontinuous and geodesic convex function on a Hadamard manifold \({\mathbb {M}}\) and the domain of f, \(\mathrm{D}(f) = {\mathbb {M}}\). Then, the subdifferential \(\partial f\) of f is a maximal monotone set-valued vector field.
Example 5.4
Consider \({\mathbb {M}} = {\mathbb {R}}_{++}^n=\{x=(x_i)\in {\mathbb {R}}^n : x_i>0, i=1,2,\ldots ,n\}\) and \(({\mathbb {R}}_{++}^n,\left\langle \cdot ,\cdot \right\rangle )\) is a Riemannian manifold endowed with the Riemannian metric \(\left\langle \cdot ,\cdot \right\rangle \) defined by
where G(x) is a positive definite symmetric square matrix of order \(n\times n\) given by
It is known that the tangent space \(T_{x}{\mathbb {M}}\) at \(x\in {\mathbb {M}}\) is equal to \({\mathbb {R}}^n\). Then, the parallel transport \(P_{y,x} : T_{x}{\mathbb {M}}\rightarrow T_{y}{\mathbb {M}}\) is the identity mapping. The Riemannian distance \(d : {\mathbb {M}}\times {\mathbb {M}}\rightarrow [0,\infty )\) is defined by
Then \(({\mathbb {R}}_{++}^n,\left\langle \cdot ,\cdot \right\rangle )\) is a Hadamard manifold. For further details, we refer [27]. The unique geodesic \(\gamma : [0,1]\rightarrow {\mathbb {M}}\) starting from \(x=(x_1,x_2,\ldots ,x_n) = \gamma (0)\) with velocity \(v={{\dot{\gamma }}}(0)\in T_{x}{\mathbb {M}}\) is defined as
Since \(\exp _{x}tv = \gamma (t)\), the inverse of the exponential map is
Let \(f:{\mathbb {R}}_{++}^n\rightarrow {\mathbb {R}}\) be a function defined by
Then, the subdifferential \(\partial f(x)\) of f is given by
Note that \(\partial f\) is a maximal monotone vector field. Consider the functions \(g,h : {\mathbb {R}}_{++}^n\rightarrow {\mathbb {R}}\) defined by \(g(x) =\frac{1}{2} \sum \nolimits _{i=1}^{n}\ln ^2x_i \) and \(h(x) = \frac{1}{4}\sum \nolimits _{i=1}^{n}(2\ln x_i -1)^2\), respectively. Then, the gradient of g and h are given by
and
respectively. Note that \(\text{ grad }\,g\) is a 1-Lipschitz continuous and monotone vector field and \(\text{ grad }\,h\) is a 2-strongly monotone vector field and 4-Lipschitz continuous for all \(x,y\in {\mathbb {R}}^{n}_{++}\) (see [4]). Then \((\partial f+\text{ grad }\,g)^{-1}(\mathbf{0})=\{(e^{-1},e^{-1},\ldots ,e^{-1}),(1,1,\ldots ,1)\}\). Consider \(A=\partial f\), \(B=\text{ grad }\,g(x)\) and \(F=\text{ grad }\,h\) in HVIP (4). For any \(y=(y_{1},y_{2},\ldots ,y_{n})\in (A+B)^{-1}(\mathbf{0})\), we have
The convergence behavior of Algorithms 1 and 2 with different initial points is given in Figs. 1, 2, 3 and 4.
We consider the following control parameters \(\alpha _{n}\) and \(\lambda _{n}\):
-
In Algorithm 1: The parameters \(\alpha _n = \frac{1}{(n+1)^p}\) and \(\lambda _n = 0.9-\frac{1}{(n+1)^q}\) with \(p+q=1\).
-
In Algorithm 2: The parameters \(\alpha _n = \frac{1}{(n+1)^p}\) for \(p<1\), \(\lambda _0 = 0.2\), \(q_n = \frac{1}{(n+1)^2}\) and \(\nu =0.9\).
We choose the random initial points by the command in the MatLab rand(n,1) for \(n =100\) and 1000. In the following figures we show the behavior of Algorithm 1 and 2 with the error function \(d(x_{n+1}, x_n)\). We run our programming codes in MATLAB r2013a on the processor Intel Core i5-6200U CPU @ 2.30 GHz \(\times \) 4 with stopping criteria \(d(x_{n+1}, x_n) < 10^{-4}\).
References
Al-Homidan, S.; Ansari, Q.H.; Babu, F.: Halpern and Mann type algorithms for fixed points and inclusion problems on Hadamard manifolds. Numer. Funct. Anal. Optim. 40(6), 621–653 (2019)
Al-Homidan, S.; Ansari, Q.H.; Babu, F.; Yao, J.C.: Viscosity method with a \(\phi \)-contraction mapping for hierarchical variational inequalities on Hadamard manifolds. Fixed Point Theory 21(2), 561–584 (2020)
Ansari, Q.H.; Babu, F.; Li, X.-B.: Variational inclusion problems in Hadamard manifolds. J. Nonlinear Convex Anal. 19(2), 219–237 (2018)
Ansari, Q.H.; Babu, F.: Proximal point algorithm for inclusion problems in Hadamard manifolds with applications. Optim. Lett. 15(3), 901–921 (2021)
Ansari, Q.H.; Babu, F.: Existence and boundedness of solutions to inclusion problems for maximal monotone vector fields in Hadamard manifolds. Optim. Lett. 14(3), 711–727 (2020)
Ansari, Q.H.; Babu, F.; Yao, J.C.: Regularization of proximal point algorithms in Hadamard manifolds. J. Fixed Point Theory Appl. 21, 25 (2019)
Ansari, Q.H.; Babu, F.; Zeeshan, M.: Existence and implicit viscosity methods for Hierarchical problems on Hadamard manifolds. J. Nonlinear Convex Anal. 21(10), 2299–2324 (2020)
Bento, G.C.; Ferreira, O.P.; Oliveira, P.R.: Proximal point method for a special class of nonconvex functions on Hadamard manifolds. Optimization 64(2), 289–319 (2012)
Chen, J.; Liu, S.; Chang, X.: Modified Tseng’s extragradient methods for variational inequality on Hadamard manifolds. Appl. Anal. 100(12), 2627–2640 (2021)
do Carmo, M.P.: Riemannian geometry. Birkhäuser, Boston, Basel, Berlin (1992)
Ferreira, O.P.; Oliveira, P.R.: Proximal point algorithm on Riemannian manifolds. Optimization 51, 257–270 (2002)
Hieu, D.V.; Anh, P.K.; Muu, L.D.; Strodiot, J.J.: Iterative regularization methods with new stepsize rules for solving variational inclusions. J. Appl. Math. Comput. 68, 571–599 (2022)
Iusem, A.N.; Mohebbi, V.: An extragradient method for vector equilibrium problems on Hadamard manifolds. J. Nonlinear Var. Anal. 5(3), 459–476 (2021)
Khammahawong, K.; Kumam, P.; Chaipunya, P.; Martinez-Moreno, J.: Tseng’s methods for inclusion problems on Hadamard manifolds. Optimization (2021). https://doi.org/10.1080/02331934.2021.1940179
Li, C.; López, G.; Martín-Márquez, V.: Resolvent of set-valued monotone vector fields in Hadamard manifold. Set-valued. Anal 19, 361–383 (2011)
Li, C.; López, G.; Martín-Márquez, V.: Monotone vector fields and the proximal point algorithm on Hadamard manifolds. J. Lond. Math. Soc. 79, 663–683 (2009)
Li, C.; López, G.; Martín-Márquez, V.: Iterative algorithms for nonexpansive mappings on Hadamard manifolds. Taiwan. J. Maths. 14, 541–559 (2010)
Li, C.; Yao, J.C.: Variational inequalities for set-valued vector fields on Riemannian manifolds: convexity of the solution set and the proximal point algorithm. SIAM J. Control Optim. 50(4), 2486–2514 (2012)
Liu, H.; Yang, J.: Weak convergence of iterative methods for solving quasimonotone variational inequalities. Comput. Optim. Appl. 77, 491–508 (2020)
Németh, S.Z.: Monotone vector fields. Publ. Math. Debrecen 54, 437–449 (1999)
Németh, S.Z.: Variational inequalities on Hadamard manifolds. Nonlinear Anal. 52, 1491–1498 (2003)
da Cruz Neto, J.X.; Ferreira, O.P.; Lucambio, P.R.: Monotone point-to-set vector fields. Balkan J. Geom. Appl. 5(1), 69–79 (2000)
Rapcsák, T.: Smooth nonlinear optimization in \({\mathbb{R}}^{n}\). Kluwer Academic Publishers Dordrecht, Boston (1997)
Rockafellar, R.T.: On the maximality of sums of nonlinear monotone operators. Trans. Am. Math. Soc. 149, 75–88 (1970)
Sakai, T.: Riemannian geometry, translations of mathematical monographs. Amer. Math. Soc, Providence (1996)
Tang, G.J.; Huang, N.J.: An inexact proximal point algorithm for maximal monotone vector fields on Hadamard manifolds. Oper. Res. Lett. 41, 586–591 (2013)
Udriste, C.: Convex functions and optimization methods on Riemannian manifolds. Kluwer Academic Publishers, Dordrecht, Boston, London (1994)
Wang, J.H.; Lopez, G.; Martín-Márquez, V.; Li, C.: Monotone and accretive vector fields on Riemannian manifolds. J. Optim. Theory Appl. 146, 691–708 (2010)
Wang, J.; Li, C.; Lopez, G.; Yao, J.C.: Convergence analysis of inexact proximal point algorithm on Hadamard manifolds. J. Global Optim. 61, 553–573 (2015)
Xu, H.: Another control condition in an iterative method for nonexpansive mappings. Bull. Austral. Math. Soc. 65, 109–113 (2002)
Funding
In this research, Moin Uddin was supported by a research fellowship from UGC, file no. 16-9 (June 2019)/2019 (NET/CSIR).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Informed consent statement
Not applicable.
Conflict of interest
The authors declare no conflict of interest.
Data availability statement
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ansari, Q.H., Babu, F. & Uddin, M. Regularization methods for hierarchical variational inequality problems on Hadamard manifolds. Arab. J. Math. 12, 309–330 (2023). https://doi.org/10.1007/s40065-022-00395-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40065-022-00395-9




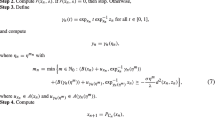
 is closed and geodesic convex.
is closed and geodesic convex.


