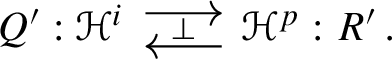Abstract
Simplicial presheaves on cartesian spaces provide a general notion of smooth spaces. There is a corresponding smooth version of the singular complex functor, which maps smooth spaces to simplicial sets. We consider the localisation of the (projective or injective) model category of smooth spaces at the morphisms which become weak equivalences under the singular complex functor. We prove that this localisation agrees with a motivic-style \(\mathbb {R}\)-localisation of the model category of smooth spaces. Further, we exhibit the singular complex functor for smooth spaces as one of several Quillen equivalences between model categories for spaces and the above \(\mathbb {R}\)-local model category of smooth spaces. In the process, we show that the singular complex functor agrees with the homotopy colimit functor up to a natural zig-zag of weak equivalences. We provide a functorial fibrant replacement in the \(\mathbb {R}\)-local model category of smooth spaces and use this to compute mapping spaces in terms of singular complexes. Finally, we explain the relation of our fibrant replacement to the concordance sheaf construction introduced recently by Berwick-Evans, Boavida de Brito and Pavlov.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and overview
Topological spaces and simplicial sets can be used to construct the same homotopy theory. This is made rigorous by the fact that the singular complex and geometric realisation functors form a Quillen equivalence between the standard model structure on the category \(\mathscr {T}\text {op}\) of topological spaces and the Kan–Quillen model structure on the category \({\mathscr {S}\text {et}_{\Delta }}\) of simplicial sets. Both of these model categories formalise what is often called the homotopy theory of spaces, or \(\infty \)-groupoids (which are the same according to Grothendieck’s homotopy hypothesis). The two models differ significantly in their features, though, in that topological spaces encode homotopies via the notion of continuity, while simplicial sets are inherently combinatorial. Consequently, each of these two models for the homotopy theory of spaces has its own merits in different contexts and applications.
Apart from continuity or combinatorics, another important feature spaces can possess, and which is relevant in many problems in mathematics, is smoothness. The prime example of a category of smooth spaces is the category \({\mathscr {M}\text {fd}}\) of manifolds and smooth maps, which underlies much of geometry. There exists a notion of smooth homotopy within the category \({\mathscr {M}\text {fd}}\), and one can find smooth versions of many topological concepts, such as cohomology, which are invariant under these smooth homotopies. However, the category \({\mathscr {M}\text {fd}}\) is poorly behaved in many ways. For instance, it is far from being complete or cocomplete, thus making it unable to admit a model structure in the sense of Quillen [40].
The way to cure this is to weaken—and therefore to generalise—the concept of a manifold. Here, we take the following approach to smooth spaces, with the main goal of simultaneously capturing the notions of manifold and (higher) stack. We start from the category \({\mathscr {C}\text {art}}\) of cartesian spaces: its objects are all smooth manifolds that are diffeomorphic to \(\mathbb {R}^n\) for any \(n \in \mathbb {N}_0\). Its morphisms are all smooth maps between these manifolds. We define a smooth space to be a simplicial presheaf on \({\mathscr {C}\text {art}}\)—informally, we understand the sections of a simplicial presheaf over \(c \in {\mathscr {C}\text {art}}\) as c-parameterised families of simplices in a space. We denote the category of simplicial presheaves on \({\mathscr {C}\text {art}}\) by \(\mathscr {H}\). It contains many geometrically interesting objects that are not manifolds or even diffeological spaces [31] (for instance the presheaf of k-forms, or the simplicial presheaf of G-bundles with connection, for any Lie group G). The category of manifolds, the category of diffeological spaces and the category of simplicial sets each include fully faithfully into \(\mathscr {H}\).
The category \(\mathscr {H}\) carries two natural model structures, namely the projective and the injective model structure on functors \({\mathscr {C}\text {art}}^\text {op}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\) (where the category \({\mathscr {S}\text {et}_{\Delta }}\) of simplicial sets carries the Kan–Quillen model structure). We denote the projective and injective model categories by \(\mathscr {H}^p\) and \(\mathscr {H}^i\), respectively, and we write \(\mathscr {H}^{p/i}\) to refer to either of these model structures simultaneously. The projective and injective model structures are canonically Quillen equivalent via the identity functors \(\mathscr {H}^p \rightleftarrows \mathscr {H}^i\), but they are not Quillen equivalent to \({\mathscr {S}\text {et}_{\Delta }}\). In that sense, the model structures \(\mathscr {H}^{p/i}\) do not yet define smooth versions of the homotopy theory of spaces. To achieve that, one needs a weaker notion of equivalence in \(\mathscr {H}\).
There exist (at least) two candidates for such weakened versions of equivalences in \(\mathscr {H}\). First, in [25, 38] a notion of weak equivalence has been introduced on sheaves on \({\mathscr {M}\text {fd}}\) as follows: let \(\Delta _e^k \cong \mathbb {R}^k\) denote the smooth extended (affine) k-simplex. Extending the usual face and degeneracy maps of the topological standard simplices, this gives rise to a cosimplicial cartesian space  . Via precomposition, this induces a functor from (pre)sheaves on manifolds to simplicial sets. In [25, 38], a morphism of sheaves is considered a weak equivalence of (pre)sheaves whenever it becomes a weak equivalence of simplicial sets under this functor. We adapt this to our set-up as follows: for technical reasons, we work with presheaves on cartesian spaces rather than manifolds, and we work with simplicial (pre)sheaves instead of ordinary (pre)sheaves. Let
. Via precomposition, this induces a functor from (pre)sheaves on manifolds to simplicial sets. In [25, 38], a morphism of sheaves is considered a weak equivalence of (pre)sheaves whenever it becomes a weak equivalence of simplicial sets under this functor. We adapt this to our set-up as follows: for technical reasons, we work with presheaves on cartesian spaces rather than manifolds, and we work with simplicial (pre)sheaves instead of ordinary (pre)sheaves. Let  denote the diagonal functor. We define the smooth singular complex functor as the composite
denote the diagonal functor. We define the smooth singular complex functor as the composite
where the first functor evaluates \(F \in \mathscr {H}\) on the extended simplices to obtain a bisimplicial set, of which the second functor then takes the diagonal. Let \(S_e^{-1}(W_{\mathscr {S}\text {et}_{\Delta }})\) denote the class of morphisms in \(\mathscr {H}\) that are mapped to a weak equivalence by \(S_e\). The generalisation to simplicial presheaves of the homotopy theory from [25, 38] is then the left Bousfield localisation
The second notion of weak equivalence in \(\mathscr {H}\) is motivated by motivic homotopy theory (see [16, 37, 50], for instance). Let I denote the class of all morphisms in \(\mathscr {H}\) of the form \(c \times \mathbb {R}\rightarrow c\), where c ranges over all objects in \({\mathscr {C}\text {art}}\), and where the morphism is the identity on c and collapses \(\mathbb {R}\) to the point. The left Bousfield localisation
is then a version in smooth geometry of motivic localisation. We call \(\mathscr {H}^{p/i\, I}\) the \(\mathbb {R}\)-local model category of simplicial presheaves on \({\mathscr {C}\text {art}}\), or equivalently of smooth spaces. This localisation has appeared before in [20, 44] and other works of these authors. For presheaves with values in stable \(\infty \)-categories, this type of localisation has been investigated in [6]. Our first main result is:
Theorem 1.1
There is an equality of model categories:
A large part of this paper is concerned establishing several explicit Quillen equivalences between these model categories and various model categories describing the homotopy theory of spaces. Concretely, these are: the Kan–Quillen model structure on simplicial sets \({\mathscr {S}\text {et}_{\Delta }}\), the model category of \(\Delta \)-generated topological spaces \({\Delta \mathscr {T}\text {op}}\) and the diagonal model structure on bisimplicial sets \((s{\mathscr {S}\text {et}_{\Delta }})_{diag}\). Further, we show in Proposition 3.19 that the model category \((s{\mathscr {S}\text {et}_{\Delta }})_{diag}\) coincides with the following two model categories: (1) the localisation \(L_{\Delta ^\bullet \boxtimes \Delta ^0}s{\mathscr {S}\text {et}_{\Delta }}\) of the injective model structure on bisimplicial sets \(s{\mathscr {S}\text {et}_{\Delta }}\) at the collapse morphisms \(\Delta ^n \rightarrow \Delta ^0\), for \(n \in \mathbb {N}_0\) (where both are seen as simplicial diagrams of discrete simplicial sets), and (2) the localisation \(L_{\Delta ^1 \boxtimes \Delta ^0} \mathscr {C}\mathscr {S}\mathscr {S}\) of the model category of complete Segal spaces at the collapse morphism \(\Delta ^1 \rightarrow \Delta ^0\).
To state our main theorem, we need the following notation: we let  denote the functor with sends a simplicial set to a constant simplicial diagram in \({\mathscr {S}\text {et}_{\Delta }}\). Similarly, let \(\tilde{\textsf {c}} :{\mathscr {S}\text {et}_{\Delta }}\rightarrow \mathscr {H}\) denote the functor sending a simplicial set to a constant simplicial presheaf on \({\mathscr {C}\text {art}}\). Finally, we have a functor
denote the functor with sends a simplicial set to a constant simplicial diagram in \({\mathscr {S}\text {et}_{\Delta }}\). Similarly, let \(\tilde{\textsf {c}} :{\mathscr {S}\text {et}_{\Delta }}\rightarrow \mathscr {H}\) denote the functor sending a simplicial set to a constant simplicial presheaf on \({\mathscr {C}\text {art}}\). Finally, we have a functor
where \(\text {D}c\) denotes the underlying topological space of \(c \in {\mathscr {C}\text {art}}\), and where \(|{-}| :{\mathscr {S}\text {et}_{\Delta }}\rightarrow {\Delta \mathscr {T}\text {op}}\) is the geometric realisation functor. If \(L : \mathscr {C}\rightarrow \mathscr {D}: R\) is a pair of adjoint functors, we also express this by the notation \(L \dashv R\). We prove:
Theorem 1.2
Each arrow in the following diagram is a Quillen equivalence (left or right as indicated)

Equalities in this diagram indicate identities of model categories. Moreover, omitting the functor \(R_e\) in the bottom-right triangle, the diagram is a commutative (up to canonical natural isomorphisms) diagram of Quillen equivalences (i.e. the left adjoints commute and the right adjoints commute).
The model structures in the top row are obtained by first localising \(\mathscr {H}^{p/i}\) at good open coverings of cartesian spaces and subsequently localising at the morphisms \(c \times \mathbb {R}\rightarrow c\). The fact that these model structures are equal to the localisation of \(\mathscr {H}^{p/i}\) only at the morphisms \(c \times \mathbb {R}\rightarrow c\) holds true because each \(c \in {\mathscr {C}\text {art}}\) is contractible (see Corollary 2.12); it would not hold true if we were working with simplicial presheaves on the category \({\mathscr {M}\text {fd}}\) of manifolds instead of \({\mathscr {C}\text {art}}\). This insight has many pleasant technical consequences. We provide a comparison with the theory of simplicial sheaves on manifolds in Appendix B.
We remark that there also exists a further model category for a theory of smooth spaces: the \(\mathbb {R}\)-local model category of enriched simplicial presheaves on a simplicial category explored in [30]Footnote 1. This model category is Quillen equivalent to \(\mathscr {H}^{p/i\, I}\) by [30, Thm. 2.4] (see also [4, Sec. 2] for applications to \(\mathbb {R}\)-local simplicial presheaves on the category of manifolds in particular).
Next, we prove various comparison results between the different functors in diagram (1.3). The most important one of these, stated below, underlines the significance of the functor \(S_e :\mathscr {H}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\): it is a model for the homotopy colimit of diagrams \({\mathscr {C}\text {art}}^\text {op}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\).
Theorem 1.4
Let \(Q^p :\mathscr {H}^p \rightarrow \mathscr {H}^p\) be a cofibrant replacement functor for the projective model structure. There is a zig-zag of natural weak equivalences
In particular, there is a natural isomorphism in \(\text {h}({\Delta \mathscr {T}\text {op}})\),
and a natural isomorphism in \(\text {h}({\mathscr {S}\text {et}_{\Delta }})\),
On a very formal level, it allows us to identify \(S_e\) as a presentation of the left adjoint in the cohesive structure on the \(\infty \)-topos of presheaves of spaces on \({\mathscr {C}\text {art}}\). This has also been observed recently in [4].
Finally, we construct a fibrant replacement functor for \(\mathscr {H}^{p/i\, I}\), motivated by the concordance sheaves introduced in [4], generalising concepts from [38]. We thereby obtain explicit access to the mapping spaces in \(\mathscr {H}^{p/i\, I}\):
Theorem 1.5
Let \(F,G \in \mathscr {H}\) be any simplicial presheaves on \({\mathscr {C}\text {art}}\). Let \(M \in {\mathscr {M}\text {fd}}\) be any manifold, and define \(\underline{M} \in \mathscr {H}\) by setting \(\underline{M}(c) = {\mathscr {M}\text {fd}}(c,M)\) for any cartesian space \(c \in {\mathscr {C}\text {art}}\). There are canonical isomorphisms
in \(\text {h}{\mathscr {S}\text {et}_{\Delta }}\), the homotopy category of spaces.
Finally, we remark that during the revision of this paper, building on Theorem 1.5 and [4], Schreiber and Sati have enhanced this result to compute the homotopy type of the mapping space \(F^{Q \underline{M}} \in \mathscr {H}\), where M is a manifold, \(\underline{M} = {\mathscr {M}\text {fd}}(-,M)\) is its associated sheaf, and \(F \in \mathscr {H}\) is a homotopy sheaf [48, Thm. 3.3.53] (this problem goes back to a question by C. Rezk and originally was answered by D. PavlovFootnote 2). Moreover, the I-localisation of \(\infty \)-sheaves on manifolds and their fibrant replacement have also been treated extensively in [1] since the first version of this paper appeared.
Outline. In Sect. 2 we define the \(\mathbb {R}\)-localisations \(\mathscr {H}^{p/i\, I}\) of \(\mathscr {H}^{p/i}\). We show that \(\mathscr {H}^{p/i\, I}\) can also be obtained as further localisations of the Čech local model structures with respect to differentiably good open coverings. We define the functor \(Re :\mathscr {H}^{p I} \rightarrow {\Delta \mathscr {T}\text {op}}\) and show that it is a left Quillen equivalence.
In Sect. 3, we study the smooth singular complex functor \(S_e :\mathscr {H}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\). We first show that \(S_e :\mathscr {H}^{p/i\, I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\) is a left Quillen equivalence. Subsequently, we establish \(S_e :\mathscr {H}^{i I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\) as a right Quillen equivalence. As an intermediate step, we relate the model categories \(\mathscr {H}^{i I}\) and \({\mathscr {S}\text {et}_{\Delta }}\) to localisations of the model category of complete Segal spaces.
Section 4 is concerned with the comparison of different ways of extracting spaces from simplicial presheaves on \({\mathscr {C}\text {art}}\). The key concept is to extend the homotopy equivalence that embeds the topological standard simplices into the smooth extended simplices to obtain natural weak equivalences between functors from \(\mathscr {H}\) to \({\mathscr {S}\text {et}_{\Delta }}\) and \({\Delta \mathscr {T}\text {op}}\). We show that, for each manifold M, the space \(S_e \underline{M}\) assigned to its associated sheaf recovers the homotopy type of M and prove Theorem 1.4.
In Sect. 5 we construct a fibrant replacement functor for \(\mathscr {H}^{p/i\, I}\) and use it to prove Theorem 1.5. We spell out the relation of this theorem to [4] and works of Dugger. Then we apply Theorem 5.6 to prove the coincidence of model structures from Theorem 1.1.
We include two appendices; Appendix A contains the explicit construction of a fibrant replacement functor for the injective model structure on \(\mathscr {H}\), which features in the proof of Theorem 1.5. Building on this, we provide a Quillen equivalence between model categories for homotopy sheaves on \({\mathscr {C}\text {art}}\) and homotopy sheaves on \({\mathscr {M}\text {fd}}\) in Appendix B.
Notation and conventions
-
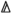 :
: -
The simplex category
- \({\mathscr {S}\text {et}_{\Delta }}\) :
-
The category of simplicial sets
- \(s{\mathscr {S}\text {et}_{\Delta }}\) :
-
The category of bisimplicial sets; when used as a model category, this will always be endowed with the Kan–Quillen model structure
- \({\Delta \mathscr {T}\text {op}}\) :
-
The model category of \(\Delta \)-generated topological spaces
- \(\underline{\mathscr {C}}(-,-)\) :
-
Simplicially enriched hom-functor in a simplicial category \(\mathscr {C}\)
- \({\mathscr {C}\text {art}}\) :
-
The category of cartesian spaces
- \({\mathscr {Y}}_c\) :
-
The image of a cartesian space \(c \in {\mathscr {C}\text {art}}\) under the Yoneda embedding
- \({\mathscr {M}\text {fd}}\) :
-
The category of smooth manifolds and smooth maps
- \(\underline{M}\) :
-
The (simplicially constant) simplicial presheaf on \({\mathscr {C}\text {art}}\) associated to a manifold M
- \({\mathscr {D}\text {fg}}\) :
-
The category of diffeological spaces
- \(\mathscr {H}\) :
-
The category of simplicial presheaves on \({\mathscr {C}\text {art}}\)
- \(\mathscr {H}^p\) :
-
Projective model structure on \(\mathscr {H}\)
- \(\mathscr {H}^i\) :
-
Injective model structure on \(\mathscr {H}\)
- \(\mathscr {H}^{p/i}\) :
-
\(\mathscr {H}\) with either one of the model structures \(\mathscr {H}^p\) or \(\mathscr {H}^i\); statements where \(\mathscr {H}^{p/i}\) is used will always mean that the statement applies to both model structures.
- \(\mathscr {H}^{p/i\,I}\) :
-
\(\mathbb {R}\)-localisation of \(\mathscr {H}^{p/i}\)
- \(\mathscr {H}^{p/i\, \ell }\) :
-
Left Bousfield localisation of \(\mathscr {H}^{p/i}\) at the (Čech nerves of) differentiably good open coverings in \({\mathscr {C}\text {art}}\)
- \(\Delta _e^k\) :
-
Extended k-simplex as an element of \({\mathscr {C}\text {art}}\)
- \(\Delta _e^*\) :
-
Evaluation of elements in \(\mathscr {H}\) on all extended simplices, produces objects in \(s{\mathscr {S}\text {et}_{\Delta }}\)
- \(\delta \) :
-
Diagonal functor
- \(\delta ^*\) :
-
Takes the diagonal of a bisimplicial set
- \(S_e\) :
-
\(= \delta ^* \circ \Delta _e^*\) the smooth singular complex functor
- \(L_e, R_e\) :
-
Left and right adjoints to \(S_e\), respectively
- Re :
-
Realisation functor \(\mathscr {H}\rightarrow {\Delta \mathscr {T}\text {op}}\)
- S :
-
Right adjoint to Re
- \({\text {Cc}}^{p/i}\) :
-
Fibrant replacement functor in \(\mathscr {H}^{p/i\, I}\)
- \(Q'\) :
-
Modified cofibrant replacement functor in \(\mathscr {H}^p\)
- \(R'\) :
-
Right adjoint to \(Q'\)
- \(\tilde{\textsf {c}}\) :
-
Takes a simplicial set to its constant simplicial presheaf on \({\mathscr {C}\text {art}}\)
- \({\text {ev}}_*\) :
-
Evaluates elements of \(\mathscr {H}\) on the final object \(* = \mathbb {R}^0 \in {\mathscr {C}\text {art}}\)
- \(\text {D}\) :
-
Sends a diffeological space to the \(\Delta \)-generated topological space induced by the plots
- \(\text {C}\) :
-
right adjoint to \(\text {D}\)
- \(\text {h}({\mathscr {M}})\) :
-
Homotopy category of a model category \({\mathscr {M}}\)
-
Given two categories \(\mathscr {C}, \mathscr {I}\), we write \({\mathscr {C}\text {at}}(\mathscr {I}, \mathscr {C})\) or \(\mathscr {C}^\mathscr {I}\) for the category of functors \(\mathscr {I}\rightarrow \mathscr {C}\).
-
We will also be working with the category
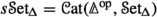 of bisimplicial sets. Our convention is always to write a bisimplicial set as a functor
of bisimplicial sets. Our convention is always to write a bisimplicial set as a functor 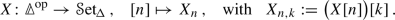
2 \(\mathbb {R}\)-local model structures and smooth spaces
We start by setting up the model-categorical background used in this paper. Partially following [44] and [18], we consider the category of simplicial presheaves on cartesian spaces with its canonical projective and injective model structures. In analogy with \({\mathbb {A}}^1\)-local homotopy theory, we localise this category at all the morphisms \(c \times \mathbb {R}\rightarrow c\), where c is any cartesian space and where the morphism is the projection onto the factor c. Extending ideas from [18], we establish several Quillen equivalences of this localised model category with the categories of simplicial sets and topological spaces.
2.1 \(\mathbb {R}\)-local model structures on simplicial presheaves
In this section we start by setting up the various model structures on simplicial presheaves that will play a role in this article. We start by introducing the central mathematical objects.
Definition 2.1
We let \({\mathscr {C}\text {art}}\) denote the (small) category of submanifolds of \(\mathbb {R}^\infty \) that are diffeomorphic to \(\mathbb {R}^n\), for any \(n \in \mathbb {N}_0\). These manifolds are called cartesian spaces. The morphisms \(c \rightarrow d\) in \({\mathscr {C}\text {art}}\) are the smooth maps \(c \rightarrow d\) between these manifolds.
In other words, \({\mathscr {C}\text {art}}\) is the full subcategory of the category \({\mathscr {M}\text {fd}}\) of smooth manifolds and smooth maps on the cartesian spaces.
Definition 2.2
Let \(\mathscr {H}:={\mathscr {C}\text {at}}({\mathscr {C}\text {art}}^\text {op}, {\mathscr {S}\text {et}_{\Delta }})\) denote the category of simplicial presheaves on \({\mathscr {C}\text {art}}\), and let \(c \mapsto {\mathscr {Y}}_c \in {\mathscr {C}\text {at}}({\mathscr {C}\text {art}}^\text {op}, {\mathscr {S}\text {et}}) \subset \mathscr {H}\) denote its Yoneda embedding. There is a fully faithful inclusion
We can view each \(c \in {\mathscr {C}\text {art}}\) as a manifold via the inclusion \({\mathscr {C}\text {art}}\subset {\mathscr {M}\text {fd}}\), and we have \(\underline{c} = {\mathscr {Y}}_c\). We view \({\mathscr {S}\text {et}_{\Delta }}\) as endowed with the Kan–Quillen model structure. The category \({\mathscr {C}\text {art}}\) carries a Grothendieck coverage \(\tau \) of differentiably good open coverings—see [22, App. A] for details. A covering of \(c \in {\mathscr {C}\text {art}}\) in this coverage is a collection of morphisms \(\{\iota _i :c_i \rightarrow c\}_{i \in \Lambda }\) in \({\mathscr {C}\text {art}}\) such that each \(\iota _i\) is an embedding of an open subset, the images of the maps \(\iota _i\) cover c (i.e. each \(x \in c\) lies in the image of some \(\iota _i\)), and every finite intersection
with \(i_0, \ldots , i_n \in \Lambda \) is either empty or a cartesian space. We let \(\ell \) denote the class of Čech nerves in \(\mathscr {H}\) of differentiably good open coverings in \({\mathscr {C}\text {art}}\). Given a simplicial model category \({\mathscr {M}}\) and a class S of morphisms in \({\mathscr {M}}\), we denote by \(L_S {\mathscr {M}}\) the left Bousfield localisation of \({\mathscr {M}}\) at the morphisms in S (see [27] for more background).
Remark 2.4
The left Bousfield localisation of a simplicial, left proper, cellular model category is again a simplicial model category [27, Thm. 4.1.1(4)]. The model category \({\mathscr {S}\text {et}_{\Delta }}\) is both left proper and cellular (see [27, Prop. 12.1.4] for the cellular part), and these properties carry over to the projective model structure on \({\mathscr {F}\text {un}}(\mathscr {C}, {\mathscr {S}\text {et}_{\Delta }})\), where \(\mathscr {C}\) is any small category [27, Prop. 12.1.5]. The same holds true for the injective model structure on simplicial presheaves [32, p. 180]. In particular, left Bousfield localisations of \(\mathscr {H}^{p/i}\) are again simplicial. Alternatively, one can obtain these localisations as simplicial model categories using Barwick’s theory of enriched Bousfield localisations [3]. \(\triangleleft \)
Definition 2.5
We define the following model categories:
-
(1)
\(\mathscr {H}^{p/i}\) is the projective (resp. injective) model structure on \(\mathscr {H}\). We also refer to \(\mathscr {H}^{p/i}\) as the model categories of smooth spaces.
-
(2)
We define the left Bousfield localisations
$$\begin{aligned} \mathscr {H}^{p/i\, \ell } :=L_\ell \mathscr {H}^{p/i}\,. \end{aligned}$$This is the projective (resp. injective) model structure for sheaves of \(\infty \)-groupoids on \({\mathscr {C}\text {art}}\).
-
(3)
Let \(I :=\{ {\mathscr {Y}}_c \times {\mathscr {Y}}_\mathbb {R}\longrightarrow {\mathscr {Y}}_c\}_{c \in {\mathscr {C}\text {art}}}\) be the set of morphisms obtained by taking the product of the collapse map \(\mathbb {R}\rightarrow *\) with all identities \(\{1_c\}_{c \in {\mathscr {C}\text {art}}}\). We define the projective (resp. injective) \(\mathbb {R}\)-local model category of smooth spaces as the left Bousfield localisation
$$\begin{aligned} \mathscr {H}^{p/i\, I} :=L_I \mathscr {H}^{p/i}\,. \end{aligned}$$
We can further form the localisations
which agree for purely abstract reasons (localisations commute).
Remark 2.6
We interpret the localisation \(\mathscr {H}^{p/i\, I}\) as an \(\mathbb {R}\)-localisation of \(\mathscr {H}^{p/i}\) akin to motivic localisation (see, for example, [16, 32, 37, 50]). Though thinking of objects in \(\mathscr {H}\) as smooth spaces, we will mostly refer objects in \(\mathscr {H}\) by the more technically precise term of simplicial presheaves, and we will sometimes refer to fibrant objects in \(\mathscr {H}^{p/i\, I}\) as essentially constant or \(\mathbb {R}\)-local simplicial presheaves (see Proposition 2.10 for justification of this terminology). \(\triangleleft \)
Note that we use the term symmetric monoidal model category in the sense of [29, Def. 4.1.13, Def. 4.2.6]. In particular, a cartesian model category is a symmetric monoidal model category whose monoidal product is the category-theoretic product.
Proposition 2.7
All model structures in Definition 2.5 are simplicial, left proper, tractable and symmetric monoidal.
Proof
Except for the claim that the model structures are symmetric monoidal, all assertions follow from [3, Thm. 4.7], building on results in [5]. The model structures for sheaves of \(\infty \)-groupoids are symmetric monoidal by [3, Thm. 4.58]. To see that \(\mathscr {H}^{p/i\, I}\) is symmetric monoidal, observe that the objects \({\mathscr {Y}}_c\), \(c \in {\mathscr {C}\text {art}}\), form a set of homotopy generators for \(\mathscr {H}^{p/i}\). Let \(F \in \mathscr {H}^{p/i\, I}\) be a local object, and consider the internal hom object \(F^{{\mathscr {Y}}_d}\) for any \(d \in {\mathscr {C}\text {art}}\). For any of the morphisms \({\mathscr {Y}}_c \times {\mathscr {Y}}_\mathbb {R}\rightarrow {\mathscr {Y}}_c\) in I, the internal hom adjunction yields a commutative diagram of simplicially enriched hom spaces

Here we have used that \({\mathscr {C}\text {art}}\) has finite products. The bottom horizontal morphism is induced by the morphism \(c \times d \times \mathbb {R}\rightarrow c \times d\), which is an element of I. Hence, the bottom morphism is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\). Therefore, it follows from [3, Prop. 4.47] that \(\mathscr {H}^{p/i\, I}\) is symmetric monoidal. The exact same proof shows that \(\mathscr {H}^{p/i\, \ell I}\) is symmetric monoidal as well. The fact that \(\mathscr {H}^{p/i\, I \ell }\) is symmetric monoidal will follow from Corollary 2.12. \(\square \)
The injective case can also be found in [42]. We record the following two direct observations:
Proposition 2.8
There are commutative diagrams of simplicial Quillen adjunctions:

where the rightwards and downwards arrows are the left adjoints. All arrows are identity functors, and all horizontal arrows are Quillen equivalences.
Proposition 2.9
Each pair of model categories defined in Definition 2.5(1)–(4) (based on either the projective or the injective model structure), respectively, has the same weak equivalences. That is, their respective underlying relative categories agree.
The reason why we also refer to fibrant objects in \(\mathscr {H}^{p/i\, I}\) as essentially constant simplicial presheaves is the following fact (the second statement is a generalisation of [18, Lemma 3.4.2]):
Proposition 2.10
Let \(F \in \mathscr {H}\). The following statements hold true:
-
(1)
The canonical morphism \(F \otimes {\mathscr {Y}}_c \rightarrow F\) is a weak equivalence in \(\mathscr {H}^{p/i\, I}\), for every \(c \in {\mathscr {C}\text {art}}\).
-
(2)
Let \(F \in \mathscr {H}^{p/i}\) be fibrant. The following are equivalent:
-
(i)
F is fibrant in \(\mathscr {H}^{p/i\, I}\).
-
(ii)
The canonical map \(F(*) \rightarrow F(c)\) is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\), for every \(c \in {\mathscr {C}\text {art}}\).
-
(iii)
For any \(f :c \rightarrow d\) in \({\mathscr {C}\text {art}}\), the morphism \(F(f) :F(d) \rightarrow F(c)\) is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\).
-
(i)
Proof
Ad (1): By Proposition 2.9, it suffices to show this for \(\mathscr {H}^{i I}\). There, every object is cofibrant (since every object in \({\mathscr {S}\text {et}_{\Delta }}\) is cofibrant), so that the functor \(F \otimes (-) :\mathscr {H}^{i I} \rightarrow \mathscr {H}^{i I}\) is left Quillen. Thus, it suffices to show that the morphism \({\mathscr {Y}}_c \rightarrow *\) is a weak equivalence. Since \(c \cong \mathbb {R}^n\) for some \(n \in \mathbb {N}_0\), we can reduce to the case where \(c = \mathbb {R}^n\).
We can write the collapse morphism \(\mathbb {R}^n \rightarrow *\) as a composition
where each arrow is an element of I. Thus, the claim follows.
Ad (2): Condition (ii) implies that F is fibrant in \(\mathscr {H}^{p/i\, I}\), i.e. condition (i): since \({\mathscr {C}\text {art}}\) has finite products, we have a commutative triangle

for any \(c \in {\mathscr {C}\text {art}}\). The fact that F is I-local thus follows from the two-out-of-three property of weak equivalences in \({\mathscr {S}\text {et}_{\Delta }}\).
We now show that (i) implies (ii): By part (1) we know that for each \(c \in {\mathscr {C}\text {art}}\), the morphism \({\mathscr {Y}}_c \rightarrow *\) is a weak equivalence in \(\mathscr {H}^{p/i\, I}\). The claim then follows from the enriched Yoneda Lemma: the top arrow in the commutative diagram

is a weak equivalence since \(\mathscr {H}^{p/i\, I}\) is simplicial (Proposition 2.7), so that \(\underline{\mathscr {H}}(-,F)\) is a right Quillen functor. As representables are cofibrant in \(\mathscr {H}^{p/i\, I}\), it follows that the functor \(\underline{\mathscr {H}}(-,F)\) preserves the weak equivalence \({\mathscr {Y}}_c \overset{\sim }{\longrightarrow }*\).
Finally, it is clear that (iii) implies (ii), and the converse implication follows readily by combining the fact that any morphism f in \({\mathscr {C}\text {art}}\) fits into a commutative triangle

with the two-out-of-three property of weak equivalences. \(\square \)
Our definitions of model structures on \(\mathscr {H}\) are redundant, by the following useful theorem:
Theorem 2.11
[33, Prop. E.1.10] Let \({\mathscr {M}}\) and \({\mathscr {M}}'\) be two model categories with the same underlying category. Then, \({\mathscr {M}}\) and \({\mathscr {M}}'\) coincide as model categories if and only if they have the same cofibrations and the same fibrant objects.
Corollary 2.12
We have the following identities of model categories:
In particular, every Čech-local weak equivalence is an I-local weak equivalence.
Proof
By their construction as left Bousfield localisations, all of the above three model categories have the same cofibrations. Thus, it suffices to check that their fibrant objects coincide.
An object \(F \in \mathscr {H}^{p/i\, \ell I}\) is fibrant if and only if it is fibrant in \(\mathscr {H}^{p/i\, \ell }\) and satisfies that the canonical map
is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\), for every \(c \in {\mathscr {C}\text {art}}\). That is, an object in \(\mathscr {H}^{p/i\, \ell I}\) is fibrant precisely if it is fibrant in both \(\mathscr {H}^{p/i\, \ell }\) and in \(\mathscr {H}^{p/i\, I}\). In particular, this implies that F is fibrant also in \(\mathscr {H}^{p/i\, I}\).
To prove the converse, we first introduce some notation. Given a set S, let \(S^{[\cdot ]} \in {\mathscr {S}\text {et}_{\Delta }}\) denote the simplicial set whose n-simplices are \(n{+}1\)-tuples \((i_0, \ldots , i_n) \in S^{n+1}\) of elements in S; its i-th face maps forget the respective i-th entry, and its j-th degeneracy maps duplicate the respective j-th entry of a tuple. Consider an object \(c \in {\mathscr {C}\text {art}}\), and let \({\mathscr {U}}= \{c_i \rightarrow c\}_{i \in \Lambda }\) be a differentiably good open covering of c. Let \(\Lambda _{ne}^n \subset \Lambda ^{n+1}\) be the subset on those \(n{+}1\)-tuples \((i_0, \ldots , i_n) \in \Lambda ^{n+1}\) such that \(C_{i_0 \cdots i_n} \ne \emptyset \) (see (2.3) for the notation). One checks that this defines a simplicial subset \(\Lambda _{ne} \subset \Lambda ^{[\cdot ]}\).
Given a projectively fibrant simplicial presheaf \(F \in \mathscr {H}\), consider the maps of simplicial sets

The second map is a weak equivalence because representables are already cofibrant.
Now, let \(F \in \mathscr {H}^{p/i\, I}\) be fibrant. We need to check that F satisfies descent with respect to the Grothendieck coverage \(\tau \) of differentiably good open coverings on \({\mathscr {C}\text {art}}\). Since F is essentially constant (i.e. fibrant in \(F \in \mathscr {H}^{p/i\, I}\)), by Proposition 2.10 the collapse maps \(c \rightarrow *\) induce weak equivalences \(F(*) \overset{\sim }{\longrightarrow }F(c)\). We thus have a commutative diagram

in \({\mathscr {S}\text {et}_{\Delta }}\). We claim that the top morphism in this diagram is an equivalence: to see this, we first note that, by assumption on the open covering \({\mathscr {U}}\), the collapse morphism \({\text {Sing}}(C_{i_0 \ldots i_n}) \rightarrow *\) is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\) for any \(i_0, \ldots , i_n \in \Lambda \) such that \(C_{i_0 \ldots i_n}\) is non-empty. For any fibrant \(K \in {\mathscr {S}\text {et}_{\Delta }}\), we thus obtain a weak equivalence
Since \(F(*) \in {\mathscr {S}\text {et}_{\Delta }}\) is fibrant, the product of these morphisms indexed by \(i_0, \ldots , i_n \in \Lambda \) is still a weak equivalence, so we obtain a commutative diagram

It follows from an application of [36, Thm. A.3.1], or by [14, Thm. 1.1] that the morphism

is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\). This is preserved by the right Quillen functor \(\underline{{\mathscr {S}\text {et}_{\Delta }}}(-,F(*))\), and thus the claim follows. \(\square \)
Remark 2.14
Corollary 2.12 fails if one considers simplicial (pre)sheaves on manifolds rather than on cartesian spaces: the proof we give above relies on the fact that the left-hand vertical morphism in Diagram (2.13) is a weak equivalence. This is true because every \(c \in {\mathscr {C}\text {art}}\) has an underlying topological space which is contractible. In contrast, consider a simplicial presheaf on manifolds, \(G :{\mathscr {M}\text {fd}}^\text {op}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\), which is projectively fibrant and I-local, i.e. it satisfies that the canonical morphism \(G(M) \rightarrow G(M \times \mathbb {R})\) is a weak equivalence for every \(M \in {\mathscr {M}\text {fd}}\). Then, G does not necessarily satisfy descent with respect to open coverings of manifolds. For instance, consider the presheaf \([-,\mathbb {S}^1]\), sending \(M \in {\mathscr {M}\text {fd}}\) to the set of homotopy classes of continuous (or smooth) maps from M to \(\mathbb {S}^1\). This is projectively fibrant and I-local. However, let \({\mathscr {U}}= \{U_i\}_{i \in \Lambda }\) be an open covering of \(M = \mathbb {S}^1\) such that each finite intersection \(U_{i_0 \ldots i_n}\) is empty or a cartesian space. Then,

but \([\mathbb {S}^1, \mathbb {S}^1] \not \simeq *\). For more details on the relation between sheaves on \({\mathscr {C}\text {art}}\) and sheaves on \({\mathscr {M}\text {fd}}\), see Appendix B. \(\triangleleft \)
Proposition 2.15
Let \(L_{\mathbb {R}^\bullet } \mathscr {H}^{p/i}\) denote the left Bousfield localisation of \(\mathscr {H}^{p/i}\) at the collapse morphisms \(\{c \rightarrow *\}_{c \in {\mathscr {C}\text {art}}}\). Further, let \(L_{\mathscr {C}\text {art}}\mathscr {H}^{p/i}\) denote the left Bousfield localisation of \(\mathscr {H}^{p/i}\) at all morphisms in \({\mathscr {C}\text {art}}\). We have the following identities of model categories:
Proof
This follows from Proposition 2.10 and Theorem 2.11. \(\square \)
2.2 Evaluation on the point
Here we present the first of several ways of extracting a space from an object \(F \in \mathscr {H}\) and show that it provides a Quillen equivalence between \(\mathscr {H}^{p/i\, I}\) and the Kan–Quillen model category \({\mathscr {S}\text {et}_{\Delta }}\).
Consider the Quillen adjunction

whose left adjoint \(\tilde{\textsf {c}}\) sends a simplicial set K to the constant simplicial presheaf with value K, and whose right adjoint evaluates a simplicial presheaf at the final object \(* \in {\mathscr {C}\text {art}}\). (Indeed, the adjunction is Quillen for both targets \(\mathscr {H}^p\) and \(\mathscr {H}^i\); in the projective case, we readily see that \({\text {ev}}_*\) is right Quillen, and in the injective case we see that \(\tilde{\textsf {c}}\) is left Quillen.) Composing this with the localisation adjunction \(\mathscr {H}^{p/i} \rightleftarrows \mathscr {H}^{p/i\, I}\), we obtain Quillen adjunctions

Lemma 2.17
Let \(e :\tilde{\textsf {c}} \circ {\text {ev}}_* \rightarrow 1_{\mathscr {H}}\) denote the counit of the adjunction (2.16). The morphism \(e_{|F} :\tilde{\textsf {c}} \circ {\text {ev}}_*(F) \longrightarrow F\) is an objectwise weak equivalence whenever \(F \in \mathscr {H}^{p/i\, I}\) is fibrant.
Proof
For any \(F \in \mathscr {H}\), the morphism \(e_{|F}\) of simplicial presheaves is the morphisms \(F(c) \rightarrow F(*)\) in \({\mathscr {S}\text {et}_{\Delta }}\) induced by the collapse maps \(c \rightarrow *\). It readily follows from Proposition 2.10 that \(e_{|F}\) is an objectwise weak equivalence whenever F is fibrant. \(\square \)
Lemma 2.18
Let \(K \in {\mathscr {S}\text {et}_{\Delta }}\) be any simplicial set. Let \(R^i :\mathscr {H}^i \rightarrow \mathscr {H}^i\) denote a fibrant replacement functor in \(\mathscr {H}^i\) (see Appendix A for an explicit construction). Then, the simplicial presheaf \(R^i \tilde{\textsf {c}}(K)\) is fibrant in \(\mathscr {H}^{i I}\).
Proof
The claim follows from Proposition 2.15 since the morphism \(\tilde{\textsf {c}}K \rightarrow R^i \tilde{\textsf {c}}K\) is an objectwise weak equivalence. \(\square \)
We can now prove a version of [18, Thm. 3.4.3] in the context of simplicial presheaves on cartesian spaces rather than on manifolds. (There, the proof is outlined for simplicial presheaves on manifolds, where several additional steps are necessary. Since we work over cartesian spaces, we can employ a slightly different strategy in our proof that allows us to avoid these additional steps.) Let \({\text {cc}}^{p/i} :1_\mathscr {H}\overset{\sim }{\longrightarrow }{\text {Cc}}^{p/i}\) be a functorial fibrant replacement in \(\mathscr {H}^{p/i\, I}\) (we provide an explicit construction in Sect. 5). Note that once a fibrant replacement \({\text {Cc}}^p\) is given, \({\text {cc}}^i :1_\mathscr {H}\overset{\sim }{\longrightarrow }{\text {Cc}}^i\) can be defined as the composition

where \(r^i :1_\mathscr {H}\rightarrow R^i\) is a fibrant replacement in the injective model structure. We always take \({\text {Cc}}^i\) to be of this form.
Lemma 2.19
For each \(K \in {\mathscr {S}\text {et}_{\Delta }}\), the morphism
is an objectwise weak equivalence.
Proof
Let R denote a fibrant replacement functor in \({\mathscr {S}\text {et}_{\Delta }}\) (such as the \({{\text {Ex}}}^\infty \)-functor). Consider the commutative diagram

The left vertical morphism is an objectwise weak equivalence. The right vertical morphism is a weak equivalence in \(\mathscr {H}^{p I}\) between fibrant objects (in \(\mathscr {H}^{p I}\)). Thus, it is also a weak equivalence in \(\mathscr {H}^p\). The bottom left object is fibrant in \(\mathscr {H}^{p I}\) by construction. Hence, the bottom horizontal morphism, which is only a weak equivalence in \(\mathscr {H}^{p I}\) a priori, is even an objectwise weak equivalence. Therefore, by the two-out-of-three property of weak equivalences in \(\mathscr {H}^p\), the top horizontal morphism is an objectwise weak equivalence as well. The injective case follows since \({\text {cc}}^i\) is the composition of this morphism by the objectwise weak equivalence \(r^i_{\tilde{\textsf {c}} K}\). \(\square \)
Theorem 2.20
The Quillen adjunction \(\tilde{\textsf {c}} \dashv {\text {ev}}_*\) from (2.16) is a Quillen equivalence.
Proof
We will show that both the derived unit and derived counit of the Quillen adjunction \(\tilde{\textsf {c}} \dashv {\text {ev}}_*\) are weak equivalences. This implies the claim by [29, Prop. 1.3.13]. For the derived counit, let \(F \in \mathscr {H}^{p/i\, I}\) be fibrant. Since all objects in \({\mathscr {S}\text {et}_{\Delta }}\) are cofibrant, it suffices to check that

is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\), where \(e_{|F}\) is the component at F of the counit of \(\tilde{\textsf {c}} \dashv {\text {ev}}_*\). This holds true by Lemma 2.17. For the derived unit, let \(K \in {\mathscr {S}\text {et}_{\Delta }}\) and consider the composition

The morphism \(\eta _K\) is an isomorphism, and the morphism \({\text {cc}}^{p/i}_{\tilde{\textsf {c}} K}\) is an objectwise weak equivalence by Lemma 2.19. \(\square \)
Corollary 2.21
Let \(W_{\mathscr {S}\text {et}_{\Delta }}\) denote the weak equivalences in \({\mathscr {S}\text {et}_{\Delta }}\) and \(W_I\) those in \(\mathscr {H}^{p/i\, I}\). The functor \(\tilde{\textsf {c}}\) preserves and reflects weak equivalences as a functor of relative categories \(({\mathscr {S}\text {et}_{\Delta }}, W_{\mathscr {S}\text {et}_{\Delta }}) \longrightarrow (\mathscr {H}, W_I)\).
Example 2.22
Let G be a Lie group with Lie algebra \({\mathfrak {g}}\). Consider the object \({\mathscr {B}\text {un}}_{G,0}^\nabla \in \mathscr {H}^p\), whose value on \(c \in {\mathscr {C}\text {art}}\) is the nerve of the following groupoid (in particular, \({\mathscr {B}\text {un}}_{G,0}^\nabla \) is fibrant in \(\mathscr {H}^p\) by construction): its objects are \({\mathfrak {g}}\)-valued 1-forms \(A \in \Omega ^1(c,{\mathfrak {g}})\) such that \(\text {d}A + \frac{1}{2} [A,A] = 0\), and its morphisms \(A \rightarrow A'\) are smooth maps \(g :c \rightarrow G\) such that \(A' = {\text {Ad}}(g^{-1}) \circ A + g^* \mu _G\), where \(\mu _G\) is the Maurer-Cartan form on G. In other words, A is a flat G-connection on a trivial principal G-bundle on c, and g is equivalently a morphism of flat principal G-bundles on c. In particular, any such morphism g is actually a constant map \(g :c \rightarrow G\). Observe that \({\mathscr {B}\text {un}}_{G,0}^\nabla (*)\) is the nerve of the groupoid with one object and the group underlying G as its morphisms. It hence follows that the functor \({\mathscr {B}\text {un}}_{G,0}^\nabla (*) \longrightarrow {\mathscr {B}\text {un}}_{G,0}^\nabla (c)\) is fully faithful (on the underlying groupoids), for any \(c \in {\mathscr {C}\text {art}}\). Since any flat G-bundle on c is isomorphic to the trivial flat G-bundle (because \(c \cong \mathbb {R}^n\) for some \(n \in \mathbb {N}_0\)), the functor \({\mathscr {B}\text {un}}_{G,0}^\nabla (*) \longrightarrow {\mathscr {B}\text {un}}_{G,0}^\nabla (c)\) is also essentially surjective. Since the nerve of an equivalence of groupoids is an equivalence of Kan complexes, it follows that \({\mathscr {B}\text {un}}_{G,0}^\nabla \) is a fibrant object in \(\mathscr {H}^{p I}\). \(\triangleleft \)
2.3 Topological realisation
In this subsection we further build on and extend ideas from [18] to investigate a second way of obtaining a space from a simplicial presheaf on \({\mathscr {C}\text {art}}\). This time, we send a simplicial presheaf to a certain coend valued in topological spaces.
More precisely, we let \({\Delta \mathscr {T}\text {op}}\) denote the category of \(\Delta \)-generated topological spaces (see [17, 51] for background). We will be working with \({\Delta \mathscr {T}\text {op}}\) as our choice of category of topological spaces throughout; however, most of the theory in this paper also works with the category of Kelley spaces (also known as k-spaces; see, for instance, [29]), except for where we work explicitly with diffeological spaces (Lemma 2.32, Remark 4.13).
We provide some very compact background on \(\Delta \)-generated topological spaces. A topological space X is \(\Delta \)-generated precisely if its topology coincides with the final topology induced by all continuous maps \(|\Delta ^n| \rightarrow X\), for all \(n \in \mathbb {N}_0\). (Here, \(|\Delta ^n|\) is the standard topological n-simplex.) In particular, the category of \(\Delta \)-generated topological spaces and continuous maps, denoted \({\Delta \mathscr {T}\text {op}}\), is cartesian closed [51]. The product in \({\Delta \mathscr {T}\text {op}}\), however, is not the usual product of topological spaces—one has to pass to the \(\Delta \)-generated topology after taking the usual product of topological spaces.
The category \({\Delta \mathscr {T}\text {op}}\) carries a cofibrantly generated model structure, having the same generating cofibrations and generating trivial cofibrations as the standard model structure on topological spaces [17, 21, 26, 49]. The geometric realisation functor \(|{-}| :{\mathscr {S}\text {et}_{\Delta }}\rightarrow {\Delta \mathscr {T}\text {op}}\) takes values in \(\Delta \)-generated spaces, since \({\Delta \mathscr {T}\text {op}}\) is closed under colimits of topological spaces and contains \(|\Delta ^n|\) for each \(n \in \mathbb {N}_0\). By construction of the model structure on \({\Delta \mathscr {T}\text {op}}\), the induced adjunction \(|{-}| : {\mathscr {S}\text {et}_{\Delta }}\rightleftarrows {\Delta \mathscr {T}\text {op}}: {\text {Sing}}\) is a Quillen adjunction (\(|{-}|\) sends generating (trivial) cofibrations to (trivial) cofibrations). Further, by the same proof as in [29, Lemma 3.18], it follows that \(|{-}|\) preserves finite products. Then, the proof of [29, Prop. 4.2.11] applies as well, showing that \({\Delta \mathscr {T}\text {op}}\) is a symmetric monoidal (even cartesian) model category. It also follows that \({\Delta \mathscr {T}\text {op}}\) is a simplicial model category and that \(|{-}|\) is a monoidal left Quillen functor. Finally, the Quillen adjunction \(|{-}| \dashv {\text {Sing}}\) is even a Quillen equivalence, since the inclusion of \({\Delta \mathscr {T}\text {op}}\) into Kelley spaces (or all topological spaces) is a Quillen equivalence [17]; the claim then follows from the two-out-of-three property of Quillen equivalences.
In this section, we provide a left Quillen equivalence \(\mathscr {H}^{p I} \rightarrow {\Delta \mathscr {T}\text {op}}\). The main ideas for this section stem from [18]; there the full proof is technically rather involved. Again, we circumvent these problems here by working over cartesian spaces rather than over the category of manifolds.
Let \({\mathscr {D}\text {fg}}\) denote the category of diffeological spaces (see [31, 47]); we use the conventions of [9], so that \({\mathscr {D}\text {fg}}\) is the full subcategory of \({\mathscr {C}\text {at}}({\mathscr {C}\text {art}}^\text {op}, {\mathscr {S}\text {et}})\) on the concrete sheaves with respect to the Grothendieck coverage \(\tau \) (see the beginning of Sect. 2.1). Concretely, a diffeological space can be defined as a pair \((X, \text {Plot}_X)\), where \(X \in {\mathscr {S}\text {et}}\), and where \(\text {Plot}_X\) assigns to every cartesian space \(c \in {\mathscr {C}\text {art}}\) a subset \(\text {Plot}_X(c) \subset {\mathscr {S}\text {et}}(c,X)\) of the maps from the underlying set of c to X. These maps are called plots of X and have to satisfy that
-
(1)
\(\text {Plot}_X(*) = X\) (every constant map is a plot),
-
(2)
for every \(f \in {\mathscr {C}\text {art}}(c,d)\) and every \(g \in \text {Plot}_X(d)\), we have that \(g \circ f \in \text {Plot}_X(c)\) (i.e. \(\text {Plot}_X\) is a presheaf on \({\mathscr {C}\text {art}}\)), and
-
(3)
the presheaf \(\text {Plot}_X\) is a sheaf with respect to \(\tau \).
We will often identify a diffeological space \((X,\text {Plot}_X)\) with the sheaf it defines (see [9] for more background), and we will denote this simply by X.
Example 2.23
For any manifold \(M \in {\mathscr {M}\text {fd}}\), the presheaf \(\underline{M}\), given by \(c \mapsto {\mathscr {M}\text {fd}}(c,M)\), is a diffeological space. In particular, this applies to every cartesian space \(d \in {\mathscr {C}\text {art}}\); for these, we have \(\underline{d} = {\mathscr {Y}}_d\) as (pre)sheaves on \({\mathscr {C}\text {art}}\). \(\triangleleft \)
Definition 2.24
Let \(\text {D}:{\mathscr {D}\text {fg}}\rightarrow {\Delta \mathscr {T}\text {op}}\) be the functor defined as follows: for \(X \in {\mathscr {D}\text {fg}}\), we let \(\text {D}X\) be the underlying set of the diffeological space \(X \in {\mathscr {D}\text {fg}}\), endowed with the final topology defined by its plots \(c \rightarrow X\), where c ranges over all cartesian spaces. A morphism \(f \in {\mathscr {D}\text {fg}}(X,Y)\) is sent to the map it defines on the sets underlying X and Y. We call \(\text {D}\) the diffeological topology functor and \(\text {D}(X)\) the underlying topological space of X.
The \(\Delta \)-generated topological spaces are in fact precisely those topological spaces that arise as the underlying topological spaces of diffeological spaces [10, 49].
Proposition 2.25
[11, 49] There exists an adjunction

where (under the embedding of \({\mathscr {D}\text {fg}}\) into presheaves on \({\mathscr {C}\text {art}}\)) we have \(\text {C}(T)(c) = {\Delta \mathscr {T}\text {op}}(c, T)\) for any topological space T and any cartesian space c.
The following proposition consists of results that can already be found in [10]; we only include the proofs here for completeness.
Proposition 2.26
Let \((-) \times (-)\) denote the product in \({\Delta \mathscr {T}\text {op}}\), and let \((-) \times ^t (-)\) denote the usual product of topological spaces. The functor \(\text {D}\) has the following properties:
-
(1)
For any manifold M, the space \(\text {D}(\underline{M})\) coincides with the underlying topological space of M.
-
(2)
For any manifolds \(M, N \in {\mathscr {M}\text {fd}}\), the canonical maps \(\text {D}(\underline{M} \times \underline{N}) \rightarrow \text {D}\underline{M} \times \text {D}\underline{N} \rightarrow \text {D}\underline{M} \times ^t \text {D}\underline{N}\) are homeomorphisms.
-
(3)
\(\text {D}:{\mathscr {D}\text {fg}}\rightarrow {\Delta \mathscr {T}\text {op}}\) preserves finite products.
Proof
Part (1) is [11, Example 3.7]: it is clear that any subset \(U \subset M\) which is open in the manifold topology is also open in the diffeological topology. Conversely, if U is open in \(\text {D}(\underline{M})\), then its intersection with all images of charts of M must be open. As these images form a basis for the manifold topology, U is open in the manifold topology.
Part (2) follows readily from Part (1) together with the fact that \(M \times N\) is again a manifold.
Part (3) is merely [10, Lemma 4.1] and the remarks following that lemma. For completeness, we fill in the details omitted there. In [10] it is proven that the natural map \(\text {D}(X \times Y) \rightarrow \text {D}X \times \text {D}Y\) is a homeomorphism whenever \(\text {D}X\) is locally compact Hausdorff. Since \(\text {D}\underline{c}\) is locally compact Hausdorff for any \(c \in {\mathscr {C}\text {art}}\), and since \(\text {D}\) preserves colimits, we have the following canonical isomorphisms in \({\Delta \mathscr {T}\text {op}}\): let \(X, Y \in {\mathscr {D}\text {fg}}\) be arbitrary. Using that \({\mathscr {D}\text {fg}}\) and \({\Delta \mathscr {T}\text {op}}\) are cartesian closed, we compute
In the third isomorphism we have used the above-mentioned result [10, Lemma 4.1]. \(\square \)
Remark 2.27
We point out that we only use manifolds without boundary or corners here. For manifolds with boundary, part (1) of Proposition 2.26 fails—see, for instance, [11, Cor. 4.47]. \(\triangleleft \)
Since each cartesian space \(c \in {\mathscr {C}\text {art}}\) is diffeomorphic to \(\mathbb {R}^n\) for some \(n \in \mathbb {N}_0\), and since \(\mathbb {R}^n\) is (isomorphic to) a CW complex for any \(n \in \mathbb {N}_0\), it follows that \(\text {D}\underline{c}\) is cofibrant in \({\Delta \mathscr {T}\text {op}}\) for every \(c \in {\mathscr {C}\text {art}}\). We have the following version of [20, Prop. 2.3]:
Theorem 2.28
There exists a Quillen adjunction \(Re \dashv S\), sitting inside a weakly commutative diagram

Further, there is a canonical natural isomorphism \(Re \circ {\mathscr {Y}}\cong \text {D}\).
Proof
The functor Re is defined as the (enriched) left Kan extension of \(\text {D}\) along \({\mathscr {Y}}\) in diagram (2.29). Explicitly, we can write
Since \(\text {D}c\) is cofibrant in \({\Delta \mathscr {T}\text {op}}\) and \({\text {Sing}}:{\Delta \mathscr {T}\text {op}}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\) is right Quillen, it follows that S maps fibrations (resp. trivial fibrations) in \({\Delta \mathscr {T}\text {op}}\) to objectwise fibrations (resp. trivial fibrations) in \(\mathscr {H}\). Thus, S is right Quillen.
For the second claim, we observe the canonical isomorphisms
for all \(d \in {\mathscr {C}\text {art}}\). The statement now follows from Proposition 2.26(1). \(\square \)
Lemma 2.31
The adjunction \(Re \dashv S\) has the following properties:
-
(1)
It is a simplicial adjunction.
-
(2)
S is monoidal.
Proof
Part (1) holds true since geometric realisation preserves finite products of simplicial sets and since the functor \(K \otimes (-) :{\Delta \mathscr {T}\text {op}}\rightarrow {\Delta \mathscr {T}\text {op}}\) is a left adjoint, for any \(K \in {\mathscr {S}\text {et}_{\Delta }}\). Part (2) holds true since S is right adjoint and \({\Delta \mathscr {T}\text {op}}\) is cartesian monoidal. \(\square \)
Lemma 2.32
Consider the fully faithful inclusion \(\iota :{\mathscr {D}\text {fg}}\hookrightarrow {\mathscr {C}\text {at}}({\mathscr {C}\text {art}}^\text {op}, {\mathscr {S}\text {et}}) \hookrightarrow \mathscr {H}\). The diagram

commutes up to natural isomorphism. In particular, for any manifold \(M \in {\mathscr {M}\text {fd}}\), \(Re \underline{M}\) is homeomorphic to the underlying topological space of M.
Proof
For \(X \in {\mathscr {D}\text {fg}}\), we have canonical natural isomorphisms
and
Combining this with Proposition 2.26 completes the proof. \(\square \)
Proposition 2.33
The pair \(Re \dashv S\) induces a Quillen adjunction

Proof
By [27, Props. 3.1.6, 3.3.18], it suffices to check that Re sends the morphisms \({\mathscr {Y}}_c \times {\mathscr {Y}}_\mathbb {R}\rightarrow {\mathscr {Y}}_c\) to weak equivalences. Since Re preserves products of representables (by Proposition 2.26 and (2.29)), it even suffices to check that Re sends the morphism \({\mathscr {Y}}_\mathbb {R}\rightarrow *\) to a weak equivalence. That it does so is evident from (2.29). \(\square \)
Proposition 2.34
The functor Re from diagram (2.29) has the following properties:
-
(1)
If \(F \in \mathscr {H}^p\) is cofibrant, Re sends the morphism \(F \times {\mathscr {Y}}_\mathbb {R}\rightarrow F\) to a weak equivalence in \({\Delta \mathscr {T}\text {op}}\).
-
(2)
For each differentiably good open covering \({\mathscr {U}}= \{c_a \rightarrow c\}_{a \in A}\) in \({\mathscr {C}\text {art}}\), the functor Re sends the Čech nerve \({\check{C}}{\mathscr {U}}\rightarrow {\mathscr {Y}}_c\) to a weak equivalence in \({\Delta \mathscr {T}\text {op}}\).
Proof
Ad (1): The morphism is a weak equivalence in \(\mathscr {H}^{p I}\) between cofibrant objects by Proposition 2.10. Therefore, the claim follows from Proposition 2.33.
Ad (2): Let \({\check{C}}{\mathscr {U}}\rightarrow {\mathscr {Y}}_c\) denote the Čech nerve of the open covering \({\mathscr {U}}\). We view this as a morphism from a simplicial presheaf \({\check{C}}{\mathscr {U}}\) to a simplicially constant presheaf \({\mathscr {Y}}_c\). Since \({\mathscr {U}}\) is a differentiably good open covering, \({\check{C}}{\mathscr {U}}\) is levelwise a coproduct of representable presheaves on \({\mathscr {C}\text {art}}\); hence, \({\check{C}}{\mathscr {U}}\) is cofibrant in \(\mathscr {H}^p\). By construction of the Čech model structure \(\mathscr {H}^{p\ell }\), the morphism \({\check{C}}{\mathscr {U}}\rightarrow {\mathscr {Y}}_c\) is a weak equivalence in \(\mathscr {H}^{p \ell }\). By Corollary 2.12, this is also a weak equivalence in \(\mathscr {H}^{p I}\). The result now follows from Proposition 2.33 and since both \({\check{C}}{\mathscr {U}}\) and \({\mathscr {Y}}_c\) are cofibrant. \(\square \)
We now prove an important property of the model categories \(\mathscr {H}^{p/i\, I}\) which allows us to detect I-local weak equivalences. Dugger calls this property rigidity in [18].
Proposition 2.35
[18, Lemma 3.4.4] Let \(F,G \in \mathscr {H}^{p/i\, I}\) be fibrant. Then, a morphism \(\psi :F \rightarrow G\) is an I-local weak equivalence if and only if \(\psi _{|*} :F(*) \rightarrow G(*)\) is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\).
Proof
Since \(\psi \) is a morphism between local objects in a left Bousfield localisation of \(\mathscr {H}^{p/i}\), it is an equivalence in \(\mathscr {H}^{p/i\, I}\) if and only if it is an objectwise weak equivalence in \(\mathscr {H}^{p/i}\). For each \(c \in {\mathscr {C}\text {art}}\), the morphism \(c \rightarrow * = \mathbb {R}^0\) induces a commutative square

Since F and G are \(\mathbb {R}\)-local, the claim now follows from Proposition 2.10.
Theorem 2.36
There is a commutative diagram of simplicial Quillen equivalences

where \(\tilde{\textsf {c}}\), Re, and \(|{-}|\) are the left adjoints.
Proof
It is well-established that the pair \(|{-}| \dashv {\text {Sing}}\) is a simplicial Quillen equivalence (see e.g. [29]). We have also seen in Theorem 2.20 that the adjunction \(\tilde{\textsf {c}} \dashv {\text {ev}}_*\) is a simplicial Quillen equivalence. The commutativity of (2.37) follows from the definitions (2.30) of the functors Re and S, which use \(|{-}|\) and \({\text {Sing}}\), respectively. The fact that \(Re \dashv S\) is a Quillen equivalence then follows from the two-out-of-three property of Quillen equivalences. \(\square \)
Remark 2.38
A slightly different version of Theorem 2.36 has been found previously in [18, 20], working over \({\mathscr {M}\text {fd}}\) instead of \({\mathscr {C}\text {art}}\). We found that \({\mathscr {C}\text {art}}\) has several technical advantages (in particular due to Corollary 2.12) and provides a sufficiently large category of parameter spaces to describe geometric and topological structures, as Theorem 2.36 shows (see also [44] for various applications of this formalism). \(\triangleleft \)
3 The singular complex of a simplicial presheaf
In this section we introduce the smooth singular complex, sometimes also called the concordance space, of a simplicial presheaf on \({\mathscr {C}\text {art}}\). We investigate its homotopical properties—for instance, it sends smooth homotopies to simplicial homotopies—and we establish it both as a left Quillen equivalence \(\mathscr {H}^{p/i\, I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\) and as a right Quillen equivalence \(\mathscr {H}^{i I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\).
3.1 Extended simplices and the smooth singular complex
In a fashion similar to motivic homotopy theory (see e.g. [16, 37, 50]), we consider the extended affine simplices in order to build our smooth singular complex functor. However, we purely rely on the smooth manifold structure of the affine cartesian simplices rather than on their function algebras.
Definition 2.1
The extended n-simplex is the cartesian space
Face and degeneracy maps are defined as the affine linear extensions of the face and degeneracy maps of the standard simplices \(|\Delta ^n|\). The extended simplices thus define a functor  .
.
By construction, the topological standard simplex
is a subset of the extended simplex \(\Delta _e^n\), for any \(n \in \mathbb {N}_0\). This inclusion \(|\Delta ^n| \hookrightarrow \Delta _e^n\) is compatible with the face and degeneracy maps. Recalling the functor \(\text {D}:{\mathscr {D}\text {fg}}\rightarrow {\Delta \mathscr {T}\text {op}}\) from Definition 2.24, we see that there is a morphism
of functors  . In particular, the diagram
. In particular, the diagram

in \({\Delta \mathscr {T}\text {op}}\) commutes for every morphism  .
.
The extended simplices functor \(\Delta _e\) induces a Quillen adjunction

Here we have made use of [27, Thm. 15.8.7], which implies that the injective model structure on bisimplicial sets agrees with the Reedy model structure. We recall
Theorem 3.3
[43, Thm. 5.2.3] Let \({\mathscr {M}}\) be a simplicial model category. Then, the realisation functor

is a left Quillen functor with respect to the Reedy model category structure on  .
.
Proposition 3.4
Let  be the diagonal functor. There exists a canonical isomorphism
be the diagonal functor. There exists a canonical isomorphism
of functors \(s{\mathscr {S}\text {et}_{\Delta }}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\), where \(\delta ^*(X)_n = X_{n,n}\) is the pullback along the diagonal functor.
Proof
This is a standard application of the Yoneda Lemma in the (co)end calculus. \(\square \)
Corollary 3.5
The diagonal functor is a left Quillen functor

In particular, it is homotopical, i.e. it preserves all weak equivalences.
Consequently, we can define a left Quillen functor as the composition
Consider a complete and cocomplete category \(\mathscr {E}\), two categories \(\mathscr {C}, \mathscr {D}\), and a functor \(F :\mathscr {C}\rightarrow \mathscr {D}\). Recall that, in this situation, the functor \(F^* :{\mathscr {C}\text {at}}(\mathscr {D},\mathscr {E}) \longrightarrow {\mathscr {C}\text {at}}(\mathscr {C}, \mathscr {E})\) has a left adjoint \(F_!\) and a right adjoint \(F_*\), which are given by the left and the right Kan extension along F. By the construction of \(S_e\) as a composition of pullback functors which act on categories of simplicial presheaves, we infer:
Proposition 3.6
The functor \(S_e = \delta ^* \circ \Delta _e^*\) has both adjoints. We thus obtain a triple of adjunctions \(L_e \dashv S_e \dashv R_e\), where \(L_e\) and \(R_e\) are given by the compositions
The adjunction \(S_e \dashv R_e\) is a simplicial Quillen adjunction.
Definition 3.7
We call the functor \(S_e :\mathscr {H}^{p/i} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\) the smooth singular complex functor. For \(F \in \mathscr {H}\), the simplicial set \(S_e F\) is called the smooth singular complex of F.
3.2 \(S_e\) as a left Quillen equivalence
We further investigate the homotopical properties of the smooth singular complex functor \(S_e\). So far, we know that the adjunction \(S_e : \mathscr {H}^{p/i} \rightleftarrows {\mathscr {S}\text {et}_{\Delta }}: R_e\) is Quillen. Our goal here is to show that this Quillen adjunction descends to the localisation \(\mathscr {H}^{p/i\, I}\) and that there it even forms a Quillen equivalence.
Definition 3.8
Let \(F,G \in \mathscr {H}\) be two simplicial presheaves on \({\mathscr {C}\text {art}}\), and let \(f_0, f_1 :F \rightarrow G\) be a pair of morphisms. A smooth homotopy from \(f_0\) to \(f_1\) is a commutative diagram

in \(\mathscr {H}\), where the vertical inclusions are induced by the maps \(* \rightarrow \mathbb {R}\), given by \(* \mapsto 0\) and \(* \mapsto 1\).
Lemma 3.10
The functor \(S_e :\mathscr {H}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\) maps smoothly homotopic morphisms to simplicially homotopic morphisms.
Proof
The projection \((t^0,t^1) \mapsto t^0\) yields a diffeomorphism \(\psi :\Delta _e^1 \rightarrow \mathbb {R}\) of cartesian spaces. Observe that there is a morphism of simplicial sets
defined by sending the generating non-degenerate 1-simplex of \(\Delta ^1\) to the 1-simplex \(\psi \). Hence, using the fact that \(S_e\) preserves products, we apply \(S_e\) to diagram (3.9) and augment it using \(\nu \) to obtain a commutative diagram

This establishes a simplicial homotopy \(S_e h \circ (1_X \times \nu )\) from \(S_e f_0\) to \(S_e f_1\). \(\square \)
Lemma 3.10 can be seen as a generalisation of [11, Lemma 4.10] from diffeological spaces to simplicial presheaves. Indeed, the composition

is precisely the smooth singular functor from [11].
Proposition 3.11
For any \(c \in {\mathscr {C}\text {art}}\), the functor \(S_e\) sends the collapse morphism \(\textsf {c}:{\mathscr {Y}}_c \rightarrow *\) to a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\).
Proof
Let \(c \in {\mathscr {C}\text {art}}\), and let \(x \in c\) be any point. The inclusion \(x :* \rightarrow c\) induces a smooth homotopy equivalence \(* \rightleftarrows c\). The functor \(S_e\) maps this to a simplicial homotopy equivalence according to Lemma 3.10. \(\square \)
Corollary 3.12
The functor \(S_e\) induces Quillen adjunctions

Proof
Each morphism \({\mathscr {Y}}_c \times {\mathscr {Y}}_\mathbb {R}\rightarrow {\mathscr {Y}}_c\) in I is a morphism between cofibrant objects in \(\mathscr {H}^{p/i}\). Therefore, by [27, Prop. 3.3.18] it suffices to show that \(S_e\) sends each morphism in I to a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\). Since \(S_e\) preserves products, it suffices to check that \(S_e({\mathscr {Y}}_\mathbb {R}\rightarrow *)\) is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\). The claim then follows from Proposition 3.11. \(\square \)
We call a functor \((\mathscr {C}, \mathcal {W}_\mathscr {C}) \rightarrow (\mathscr {D}, \mathcal {W}_\mathscr {D})\) between relative categories homotopical if it preserves weak equivalences (see also [13, 43, 46] for more background on homotopical categories and functors).
Proposition 3.13
The functors \(S_e :\mathscr {H}^{p/i\, I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\) are homotopical.
Proof
\(S_e :\mathscr {H}^{i I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\) is homotopical because it is left Quillen and every object in \(\mathscr {H}^{i I}\) is cofibrant. The corresponding statement for the projective model structure now follows from Proposition 2.9. \(\square \)
Note, in particular, that by Proposition 2.12 the functor \(S_e\) also sends weak equivalences in the Čech local model structures \(\mathscr {H}^{p/i\, \ell }\) to weak equivalences in \({\mathscr {S}\text {et}_{\Delta }}\).
Theorem 3.14
The Quillen adjunctions

are Quillen equivalences.
Proof
We have Quillen adjunctions

and we know from Theorem 2.20 that the Quillen adjunction \(\tilde{\textsf {c}} \dashv {\text {ev}}_*\) is even a Quillen equivalence. We readily see that \(S_e \circ \tilde{\textsf {c}}\) is the identity functor on \({\mathscr {S}\text {et}_{\Delta }}\). It follows that, \(S_e \dashv R_e\) is a Quillen equivalence. \(\square \)
Corollary 3.15
The functor \(S_e\) both preserves and reflects weak equivalences as a functor of relative categories \((\mathscr {H}, W_I) \longrightarrow ({\mathscr {S}\text {et}_{\Delta }}, W_{\mathscr {S}\text {et}_{\Delta }})\).
Proof
The left Quillen equivalence \(S_e :\mathscr {H}^{iI} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\) preserves and reflects weak equivalences since every object in \(\mathscr {H}^{iI}\) is cofibrant (see e.g. [29, Prop. 1.3.16]). The statement on the level of relative categories then follows from Proposition 2.9. \(\square \)
Corollary 3.16
Any smooth homotopy equivalence in \(\mathscr {H}\) is a weak equivalence in \(\mathscr {H}^{p/i\, I}\).
Proof
By Proposition 3.10, \(S_e\) sends smooth homotopy equivalences to simplicial homotopy equivalences, which are, in particular, weak equivalences in \({\mathscr {S}\text {et}_{\Delta }}\). Thus, the claim follows from Corollary 3.15. \(\square \)
Remark 3.17
Let \(W_{\mathscr {S}\text {et}_{\Delta }}\) denote the class of weak equivalences in \({\mathscr {S}\text {et}_{\Delta }}\), and let \(S_e^{-1}(W_{\mathscr {S}\text {et}_{\Delta }})\) denote the class of morphisms in \(\mathscr {H}\) whose image under \(S_e\) is in \(W_{\mathscr {S}\text {et}_{\Delta }}\). Corollary 3.15 lets us suspect that there is an equivalence of model categories
Using properties of local weak equivalences in Bousfield localisations should allow us to prove that conjecture here already, but instead we give a very direct proof later in Theorem 5.7. \(\triangleleft \)
3.3 \(S_e\) as a right Quillen equivalence
The goal of this subsection is to establish the smooth singular functor as a right Quillen functor \(S_e :\mathscr {H}^{i I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\). Apart from having convenient technical implications on the functor \(S_e :\mathscr {H}^{i I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\), the appearance of several intermediate model structures of bisimplicial sets sheds additional light on the functor \(S_e\). We already know from Proposition 3.6 that \(S_e = \delta ^* \circ \Delta _e^*\) has a left adjoint \(L_e = \Delta _{e!} \circ \delta _!\). We will show that both its constituting functors \(\Delta _{e!}\) and \(\delta _!\) are left Quillen functors.
3.3.1 Model structures for \(\infty \)-groupoids on the category of bisimplicial sets
We start by analysing the functor \(\delta _!\) in more detail. Let

denote the spine-inclusion of the n-simplex \(\Delta ^n\), for \(n \ge 1\). (Note that for \(n = 1\) the morphism \(\iota _1\) is an isomorphism.)
We write  for the category of bisimplicial sets. There exists a bifunctor
for the category of bisimplicial sets. There exists a bifunctor
We view a bisimplicial set X as a simplicial diagram \(m \mapsto X_{m,\bullet }\) in \({\mathscr {S}\text {et}_{\Delta }}\). Let
denote the set of all spine inclusions, viewed as maps of vertically constant bisimplicial sets. Let \(J \in {\mathscr {S}\text {et}_{\Delta }}\) denote the nerve of the groupoid with two objects and a unique isomorphism between them. The following definitions are taken from [2, 28, 41].
Definition 3.18
We define the following model structures on the category \(s{\mathscr {S}\text {et}_{\Delta }}\) of bisimplicial sets:
-
(1)
We view
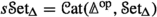 as endowed with the injective model structure. Recall that this coincides with the Reedy model structure [27].
as endowed with the injective model structure. Recall that this coincides with the Reedy model structure [27]. -
(2)
We let \({\mathscr {S}\mathscr {S}\text {p}}:=L_{\text {Sp}}s{\mathscr {S}\text {et}_{\Delta }}\) be the left Bousfield localisation of \(s{\mathscr {S}\text {et}_{\Delta }}\) at the spine inclusions. This is the model category for Segal spaces.
-
(3)
The model category for complete Segal spaces is the left Bousfield localisation \(\mathscr {C}\mathscr {S}\mathscr {S}:=L_{J \boxtimes \Delta ^0} {\mathscr {S}\mathscr {S}\text {p}}\).
Let \(L_{\Delta ^\bullet \boxtimes \Delta ^0} s{\mathscr {S}\text {et}_{\Delta }}\) denote the left Bousfield localisation of the injective model category of bisimplicial sets at all collapse morphisms \(\{\Delta ^n \boxtimes \Delta ^0 \rightarrow \Delta ^0 \boxtimes \Delta ^0\, | \, n \in \mathbb {N}_0\}\). Let  denote the left Bousfield localisation of \(s{\mathscr {S}\text {et}_{\Delta }}\) at all morphisms \(\{\varphi \boxtimes 1_{\Delta ^0} :\Delta ^n \boxtimes \Delta ^0 \rightarrow \Delta ^m \boxtimes \Delta ^0\, | \, n,m \in \mathbb {N}_0\}\). (Compare these localisations to those in Proposition 2.15.) Finally, let \(L_{\Delta ^1 \boxtimes \Delta ^0} {\mathscr {S}\mathscr {S}\text {p}}\) and \(L_{\Delta ^1 \boxtimes \Delta ^0} \mathscr {C}\mathscr {S}\mathscr {S}\) denote the left Bousfield localisations of \({\mathscr {S}\mathscr {S}\text {p}}\) and \(\mathscr {C}\mathscr {S}\mathscr {S}\), respectively, at the morphism \(\Delta ^1 \boxtimes \Delta ^0 \rightarrow \Delta ^0 \boxtimes \Delta ^0\). We will mostly be using the model category \(L_{\Delta ^\bullet \boxtimes \Delta ^0} s{\mathscr {S}\text {et}_{\Delta }}\), but for conceptual clarity and for an interpretation as model categories for \(\infty \)-groupoids, we include the following proposition.
denote the left Bousfield localisation of \(s{\mathscr {S}\text {et}_{\Delta }}\) at all morphisms \(\{\varphi \boxtimes 1_{\Delta ^0} :\Delta ^n \boxtimes \Delta ^0 \rightarrow \Delta ^m \boxtimes \Delta ^0\, | \, n,m \in \mathbb {N}_0\}\). (Compare these localisations to those in Proposition 2.15.) Finally, let \(L_{\Delta ^1 \boxtimes \Delta ^0} {\mathscr {S}\mathscr {S}\text {p}}\) and \(L_{\Delta ^1 \boxtimes \Delta ^0} \mathscr {C}\mathscr {S}\mathscr {S}\) denote the left Bousfield localisations of \({\mathscr {S}\mathscr {S}\text {p}}\) and \(\mathscr {C}\mathscr {S}\mathscr {S}\), respectively, at the morphism \(\Delta ^1 \boxtimes \Delta ^0 \rightarrow \Delta ^0 \boxtimes \Delta ^0\). We will mostly be using the model category \(L_{\Delta ^\bullet \boxtimes \Delta ^0} s{\mathscr {S}\text {et}_{\Delta }}\), but for conceptual clarity and for an interpretation as model categories for \(\infty \)-groupoids, we include the following proposition.
Proposition 3.19
The following left Bousfield localisations yield identical model categories:

Proof
By Theorem 2.11 it suffices to check that all four model categories have the same cofibrations and fibrant objects. For cofibrations, this is trivial since each of the model categories is a left Bousfield localisation of \(s{\mathscr {S}\text {et}_{\Delta }}\). It thus remains to check that the fibrant objects of the three model categories coincide.
Identity (1) is a direct consequence of the two-out-of-three property of weak equivalences.
For identity (2), let \(X \in L_{\Delta ^\bullet \boxtimes \Delta ^0} s{\mathscr {S}\text {et}_{\Delta }}\) be fibrant. That is, X is injective fibrant in \(s{\mathscr {S}\text {et}_{\Delta }}\) and the canonical map \(X_0 \rightarrow X_n\) is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\) for any \(n \in \mathbb {N}_0\). We have to show that X satisfies the Segal condition, i.e. that for every \(n \ge 2\) the spine inclusion \({\text {Sp}}_n \hookrightarrow \Delta ^n\) induces a weak equivalence
(As pointed out in [41], the strict pullback is a homotopy pullback here because X is Reedy fibrant.) Consider the commutative diagram

Since X is Reedy fibrant, the pullbacks on the right-hand side are homotopy pullbacks. Therefore, both vertical maps in (3.20) are weak equivalences. It follows by the commutativity of the diagram that X satisfies the Segal condition. Then, X is fibrant in \(L_{\Delta ^1 \boxtimes \Delta ^0} {\mathscr {S}\mathscr {S}\text {p}}\) since, by assumption, the morphism \(X_0 \rightarrow X_1\) is a weak equivalence.
Conversely, if X is fibrant in \(L_{\Delta ^1 \boxtimes \Delta ^0} {\mathscr {S}\mathscr {S}\text {p}}\), then the top horizontal morphism in diagram (3.20) is a weak equivalence because X satisfies the Segal condition, and the right-hand vertical morphism is a weak equivalence because X is injective fibrant and X is local with respect to \(\Delta ^1 \boxtimes \Delta ^0 \rightarrow \Delta ^0 \boxtimes \Delta ^0\). It thus follows by the commutativity of the diagram that also the left vertical morphism is an equivalence, for any \(n \ge 2\), so that X is fibrant in \(L_{\Delta ^\bullet \boxtimes \Delta ^0} s{\mathscr {S}\text {et}_{\Delta }}\).
For identity (3), recall that in any Segal space X there is a notion of when a morphism \(f \in X_1\) is invertible (or a ‘homotopy equivalence’ in the language of [41]). One defines the space \(X_{weq}\) of homotopy equivalences in X to be the union of those connected components of \(X_1\) that contain invertible morphisms (by [41, Lemma 5.8], if \(X \in {\mathscr {S}\mathscr {S}\text {p}}\) is fibrant, then a connected component of \(X_1\) contains a homotopy equivalence if and only if it consists purely of homotopy equivalences). For any Segal space, the degeneracy morphism \(s_0 :X_0 \rightarrow X_1\) factors as

Since every fibrant object in \(\mathscr {C}\mathscr {S}\mathscr {S}\) is also fibrant in \({\mathscr {S}\mathscr {S}\text {p}}\), this implies that every fibrant object in \(L_{\Delta ^1 \boxtimes \Delta ^0}\mathscr {C}\mathscr {S}\mathscr {S}\) is fibrant in \(L_{\Delta ^1 \boxtimes \Delta ^0}{\mathscr {S}\mathscr {S}\text {p}}\).
Conversely, let \(Y \in {\mathscr {S}\mathscr {S}\text {p}}\) be fibrant. Then, Y is local in \(L_{\Delta ^1 \boxtimes \Delta ^0}{\mathscr {S}\mathscr {S}\text {p}}\) precisely if the morphism \(s_0 :Y_0 \rightarrow Y_1\) is a weak equivalence. We need to show that, in that case, the morphism \(\widehat{s_0} :Y_0 \rightarrow Y_{weq}\) is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\). However, since \(\iota _Y :Y_{weq} \rightarrow Y\) is the inclusion of a union of connected components of \(Y_1\), diagram (3.21) and the fact that \(s_0\) is a weak equivalence imply that \(\iota _Y\) hits every connected component of \(Y_1\). Therefore, \(\iota _Y\) is a weak equivalence; it follows from the two-out-of-three property that \(\widehat{s_0} :Y_0 \rightarrow Y_{weq}\) is a weak equivalence as well. \(\square \)
Remark 3.22
Let \(X \in {\mathscr {S}\mathscr {S}\text {p}}\) be fibrant. Since \(\iota _X :X_{weq} \rightarrow X_1\) is the inclusion of a union of connected components of \(X_1\), it follows that \(\iota _X\) is a weak equivalence precisely if it is an isomorphism, i.e. precisely if \(X_{weq} = X_1\). In other words, a fibrant object in both \(L_{\Delta ^1 \boxtimes \Delta ^0} {\mathscr {S}\mathscr {S}\text {p}}\) and \(L_{\Delta ^1 \boxtimes \Delta ^0} \mathscr {C}\mathscr {S}\mathscr {S}\) is a complete Segal space with all 1-morphisms invertible. In that sense, the fibrant objects in these model categories are \(\infty \)-groupoids. The model category  can be seen as the model category of essentially constant simplicial diagrams of spaces, in analogy to how \(L_{\mathscr {C}\text {art}}\mathscr {H}^{p/i}\) describes essentially constant simplicial presheaves. \(\triangleleft \)
can be seen as the model category of essentially constant simplicial diagrams of spaces, in analogy to how \(L_{\mathscr {C}\text {art}}\mathscr {H}^{p/i}\) describes essentially constant simplicial presheaves. \(\triangleleft \)
Remark 3.23
The model structures in Proposition 3.19 further agree with the diagonal model structure on bisimplicial sets (also known as the Moerdijk model structure): these model categories have the same underlying categories, the same cofibrations, and they also have the same fibrant objects (see, for instance, [24, Sec. IV.3.3]). Thus, the claimed equality follows from Theorem 2.11. \(\triangleleft \)
We recall the following classical fact (see, for example, [24, Sec. IV.3.3]);
Proposition 3.24
The diagonal \(\delta ^* :s{\mathscr {S}\text {et}_{\Delta }}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\) induces a Quillen adjunction

From now on, we will understand the adjunction \(\delta _! \dashv \delta ^*\) as the above Quillen adjunction. There is another Quillen adjunction that relates \(L_{\Delta ^\bullet \boxtimes \Delta ^0} s{\mathscr {S}\text {et}_{\Delta }}\) to the model category of simplicial sets, in analogy with Theorem 2.20.
Proposition 3.25
Consider the adjoint pair  , where
, where  , and where \({\text {ev}}_{[0]}(X) = X_{0,\bullet }\). This satisfies:
, and where \({\text {ev}}_{[0]}(X) = X_{0,\bullet }\). This satisfies:
-
(1)
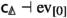 is a Quillen adjunction \({\mathscr {S}\text {et}_{\Delta }}\rightleftarrows s{\mathscr {S}\text {et}_{\Delta }}\).
is a Quillen adjunction \({\mathscr {S}\text {et}_{\Delta }}\rightleftarrows s{\mathscr {S}\text {et}_{\Delta }}\). -
(2)
Composing the Quillen adjunction from (1) with the localisation adjunction \(s{\mathscr {S}\text {et}_{\Delta }}\rightleftarrows L_{\Delta ^\bullet \boxtimes \Delta ^0} s{\mathscr {S}\text {et}_{\Delta }}\) yields a Quillen equivalence

Proof
It is straightforward to see that  preserves cofibrations and further preserves as well as reflects weak equivalences. This proves claim (1). Part (2) proceeds entirely in parallel to the proofs of Lemma 2.19 and Theorem 2.20. \(\square \)
preserves cofibrations and further preserves as well as reflects weak equivalences. This proves claim (1). Part (2) proceeds entirely in parallel to the proofs of Lemma 2.19 and Theorem 2.20. \(\square \)
Corollary 3.26
The functor  induces a functor on the underlying relative categories and detects weak equivalences.
induces a functor on the underlying relative categories and detects weak equivalences.
3.3.2 The functors \(\Delta _{e!}\) and \(L_e\)
Next, we show that \(\Delta _{e!} :s{\mathscr {S}\text {et}_{\Delta }}\rightarrow \mathscr {H}^{i I}\) is left Quillen, and that the Quillen adjunction \(\Delta _{e!} \dashv \Delta _{e*}\) descends to the localisation  . The functor \(\Delta _{e!}\) acts as
. The functor \(\Delta _{e!}\) acts as
In particular, for bisimplicial sets in the image of \((-) \boxtimes (-)\) we find that
It follows that
for any \(L \in {\mathscr {S}\text {et}_{\Delta }}\), where \(\tilde{\textsf {c}} :{\mathscr {S}\text {et}_{\Delta }}\rightarrow \mathscr {H}\) is the constant-presheaf functor.
Lemma 3.29
For any \(n \in \mathbb {N}_0\), the morphism \(\Delta _{e!}(\partial \Delta ^n \boxtimes \Delta ^0 \longrightarrow \Delta ^n \boxtimes \Delta ^0)\) is a cofibration in \(\mathscr {H}^i\).
Proof
For \(n=0,1\) this is straightforward. Consider the presentation of \(\partial \Delta ^n\) as a coequaliser,
Since \(\Delta _{e!}\) preserves colimits, we obtain
The colimit is taken in \(\mathscr {H}\) (not in \({\mathscr {D}\text {fg}}\), even though all \(\Delta _e^k\) are diffeological spaces), and so we have
for any \(c \in {\mathscr {C}\text {art}}\). In particular, any section of \(\partial \Delta _e^n\) over \(c \in {\mathscr {C}\text {art}}\) comes from some section \(f \in \Delta _e^{n-1}(c)\) of a face of \(\Delta _e^n\). Two such sections \(f,g \in \Delta _e^{n-1}(c)\) are identified precisely if they factor through the copy of \(\Delta _e^{n-2}\) that joins the respective faces of \(\Delta _e^n\) and if, further, f and g agree as maps \(c \rightarrow \Delta _e^{n-2}\).
Let \(f,g \in \partial \Delta _e^n(c)\) be any two elements, and assume that \(\iota _e^n \circ f = \iota _e^n \circ g\), where \(\iota _e^n :\partial \Delta _e^n \longrightarrow \Delta _e^n\) is the canonical morphism. Observe that \(\iota _e^n\) is injective as a map on the underlying sets \(\partial \Delta _e^n(*) \hookrightarrow \Delta _e^n(*)\). Since every section \(f :{\mathscr {Y}}_c \rightarrow \partial \Delta _e^n\) is, in particular, a map \({\mathscr {Y}}_c(*) \rightarrow \partial \Delta _e^n(*)\) of the underlying sets, and analogously a section \({\mathscr {Y}}_c \rightarrow \Delta _e^n\) is, in particular, a map \({\mathscr {Y}}_c(*) \rightarrow \Delta _e^n(*)\) of underlying sets, it follows that \(\iota _e^n :\partial \Delta _e^n \rightarrow \Delta _e^n\) is an objectwise monomorphism. \(\square \)
Remark 3.31
We point out that \(\partial \Delta _e^n\), as defined in (3.30), is not a diffeological space for \(n \ge 2\). For instance, consider a differentiably good open covering \(c = c_0 \cup c_1\) of a cartesian space c. We denote the intersection \(c_0 \cap c_1\) by \(c_{01} \in {\mathscr {C}\text {art}}\). Let \(f_i :c_i \rightarrow \Delta _e^{n-1}\) be smooth maps, for \(i = 0,1\), to adjacent faces of \(\Delta _e^n\), such that \(f_{i|c_{01}} :c_{01} \rightarrow \Delta _e^{n-2}\) factors through the \(n{-}2\)-simplex which joins the two faces. These data to not lift to a section \(f \in \partial \Delta _e^n(c)\), since such an f must factor through only one of the faces \(\partial \Delta _e^{n-1}\). That is, \(\partial \Delta _e^n\) does not satisfy the sheaf condition. \(\triangleleft \)
Let \(\mathscr {C}, \mathscr {D}, \mathscr {E}\) be categories. Recall the notion of an adjunction of two variables \(\mathscr {C}\times \mathscr {D}\rightarrow \mathscr {E}\) (see, for example, [29, Def. 4.1.12]). We will denote an adjunction of two variables only by its tensor functor \(\otimes :\mathscr {C}\times \mathscr {D}\rightarrow \mathscr {E}\). If \(\mathscr {E}\) has pushouts, then there is an induced pushout product, or box product, on morphisms: given morphisms \(f :A \rightarrow B\) in \(\mathscr {C}\) and \(g :X \rightarrow Y\) in \(\mathscr {D}\), their pushout product (relative to \(\otimes \)) is the induced morphism in \(\mathscr {E}\) given by

We recall following definitions:
Definition 3.32
[29, Def. 4.2.1] Let \(\mathscr {C}, \mathscr {D}, \mathscr {E}\) be model categories, and let \(\otimes :\mathscr {C}\times \mathscr {D}\rightarrow \mathscr {E}\) be an adjunction of two variables. Then, \(\otimes \) is a Quillen adjunction of two variables if the induced pushout product \(f,g \mapsto f \square g\) satisfies the pushout-product axiom:
-
(1)
if both f and g are cofibrations, then so is \(f \square g\), and
-
(2)
if, in addition, f or g is a weak equivalence, then so is \(f \square g\).
Definition 3.33
[29, Def. 4.2.6] A (symmetric) monoidal model category is a closed (symmetric) monoidal category \((\mathscr {C}, \otimes )\) together with a model structure on the underlying category \(\mathscr {C}\) such that:
-
(1)
the closed monoidal structure is a Quillen adjunction of two variables \(\otimes :\mathscr {C}\times \mathscr {C}\rightarrow \mathscr {C}\).
-
(2)
Let \(u \in \mathscr {C}\) be the monoidal unit, and let \(q_u :Q^\mathscr {C}u \overset{\sim }{\longrightarrow }u\) be a cofibrant replacement. Then, tensoring with any cofibrant object from the left or the right sends \(q_u\) to a weak equivalence.
Example 3.34
The model category \(s{\mathscr {S}\text {et}_{\Delta }}\) with the injective model structure is cartesian (i.e. symmetric monoidal with \(\otimes = \times \)). Similarly, each of the model categories \(\mathscr {H}^{p/i}\), \(\mathscr {H}^{p/i\, \ell }\), and \(\mathscr {H}^{p/i\, I}\) is cartesian by Proposition 2.7. In each of the monoidal model structures we encounter here, the monoidal unit is already cofibrant, so that the second axiom of Definition 3.33 is trivially satisfied. \(\triangleleft \)
The injective model structure on \(s{\mathscr {S}\text {et}_{\Delta }}\) is cofibrantly generated (see e.g. [41]), with generating cofibrations
and generating trivial cofibrations
Proposition 3.35
There is a Quillen adjunction

Proof
We have already seen in Lemma 3.29 that \(\Delta _{e!}\) sends the morphism \(\partial \Delta ^n \boxtimes \Delta ^0 \hookrightarrow \Delta ^n \boxtimes \Delta ^0\) to the injective cofibration \(\partial \Delta _e^n \hookrightarrow \Delta _e^n\) in \(\mathscr {H}^i\). Further, it follows from Equations (3.27) and (3.28) that
which is an injective cofibration, and that
which is an injective trivial cofibration.
It suffices the check that \(\Delta _{e!}\) sends the generating (trivial) cofibrations of \(s{\mathscr {S}\text {et}_{\Delta }}\) to (trivial) cofibrations in \(\mathscr {H}^i\) (see, for instance, [29, Lemma 2.1.20]). For \(n, m \in \mathbb {N}_0\), the pushout-product
is the canonical morphism

Note that, for \(A, B, C, D \in {\mathscr {S}\text {et}_{\Delta }}\), there is a canonical natural isomorphism
in \(s{\mathscr {S}\text {et}_{\Delta }}\). Thus, the above pushout-product is canonically isomorphic to to morphism

Since the functor \(\Delta _{e!}\) preserves pushouts, and using (3.27), this is sent to the morphism

which coincides with the pushout product \((\partial \Delta ^n_e \hookrightarrow \Delta ^n_e) \square (\tilde{\textsf {c}} \partial \Delta ^m \hookrightarrow \tilde{\textsf {c}} \Delta ^m)\) in \(\mathscr {H}^i\). By Lemma 3.29 and the fact that the model category \(\mathscr {H}^i\) is symmetric monoidal (even cartesian), this pushout-product is a cofibration in \(\mathscr {H}^i\). Thus, \(\Delta _{e!}\) sends the generating cofibrations of \({\mathscr {S}\text {et}_{\Delta }}\) to cofibrations. An analogous argument shows that it also sends the generating trivial cofibrations to trivial cofibrations. \(\square \)
Composing with the localisation \(\mathscr {H}^i \leftrightarrows \mathscr {H}^{i I}\), we obtain a Quillen adjunction

Proposition 3.36
The Quillen adjunction \(\Delta _{e!} : s{\mathscr {S}\text {et}_{\Delta }}\leftrightarrows \mathscr {H}^{i I} : \Delta _e^*\) descends to a Quillen adjunction

Proof
This is a direct consequence of the fact that \(\Delta _{e!}(\Delta ^n \boxtimes \Delta ^0) \cong \Delta _e^n\). The collapse morphism \(\Delta _e^n \rightarrow *\) is a weak equivalence in \(\mathscr {H}^{i I}\) by Proposition 2.10. \(\square \)
Corollary 3.37
The adjunction \(L_e : {\mathscr {S}\text {et}_{\Delta }}\rightleftarrows \mathscr {H}^{i I} : S_e\) is a Quillen adjunction.
Proof
This is a direct consequence of Proposition 3.24 and Proposition 3.36. \(\square \)
Theorem 3.38
There is a commutative triangle of Quillen equivalences

where  , \(\Delta _{e!}\), and \(\tilde{\textsf {c}}\) are the left adjoints.
, \(\Delta _{e!}\), and \(\tilde{\textsf {c}}\) are the left adjoints.
Proof
We know from Theorem 2.20 that the bottom adjunction is a Quillen equivalence, and we know from Proposition 3.25 that the left diagonal adjunction is a Quillen equivalence. Further, it is evident that the diagram of right adjoints commutes strictly. Thus, the claim follows from the two-out-of-three property of Quillen equivalences. \(\square \)
Lemma 3.39
Consider the functors \({\text {ev}}_*, S_e :\mathscr {H}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\).
-
(1)
There is a canonical natural transformation \(\gamma :{\text {ev}}_* \rightarrow S_e\).
-
(2)
The right derived natural transformation of \(\gamma \) is a natural weak equivalence.
Proof
Consider first the functors  . For any \(F \in \mathscr {H}\), the collapse map \(\Delta _e^n \rightarrow *\) induces a morphism \(\widehat{\gamma }_{|F,n} :F(*) \rightarrow F(\Delta _e^n)\) of simplicial sets. Since \(* \in {\mathscr {C}\text {art}}\) is final, this induces a natural transformation
. For any \(F \in \mathscr {H}\), the collapse map \(\Delta _e^n \rightarrow *\) induces a morphism \(\widehat{\gamma }_{|F,n} :F(*) \rightarrow F(\Delta _e^n)\) of simplicial sets. Since \(* \in {\mathscr {C}\text {art}}\) is final, this induces a natural transformation  . Applying the diagonal functor \(\delta ^*\) to this natural transformation, we obtain a natural transformation
. Applying the diagonal functor \(\delta ^*\) to this natural transformation, we obtain a natural transformation

This shows part (1). Part (2) then follows from the fact that, whenever \(F \in \mathscr {H}^{p/i\, I}\) is fibrant, the morphism \(F(*) \rightarrow F(\Delta _e^n)\) is a weak equivalence for every \(n \in \mathbb {N}_0\). Therefore, if F is fibrant, then  is an objectwise weak equivalence in \(s{\mathscr {S}\text {et}_{\Delta }}\). The claim now follows from the fact that the diagonal functor \(\delta ^*\) is homotopical. \(\square \)
is an objectwise weak equivalence in \(s{\mathscr {S}\text {et}_{\Delta }}\). The claim now follows from the fact that the diagonal functor \(\delta ^*\) is homotopical. \(\square \)
Theorem 3.40
The Quillen adjunction

is a Quillen equivalence.
Proof
Lemma 3.39 provides a natural weak equivalence between the right derived functors of \({\text {ev}}_*\) and \(S_e\). By Theorem 2.20, the functor \({\text {ev}}_*\) is a right Quillen equivalence, and it follows that so is \(S_e\). \(\square \)
Corollary 3.41
The Quillen adjunction

is a Quillen equivalence.
Proof
This follows from the fact that \(L_e = \Delta _{e!} \circ \delta _!\), together with Theorem 3.38 and the two-out-of-three property for Quillen equivalences. \(\square \)
Corollary 3.41 becomes particularly interesting in light of Proposition 3.19: it establishes a Quillen equivalence between the Kan–Quillen model structure on simplicial sets and each of the model structures in Proposition 3.19. In other words, Corollary 3.41 shows that each of the model categories from Proposition 3.19 is a model category for \(\infty \)-groupoids.
4 Comparison of spaces constructed from simplicial presheaves
In Sects. 2 and 3 we have seen several ways of extracting a space from a simplicial presheaf on \({\mathscr {C}\text {art}}\). The main goal of Sect. 4.1 is to establish comparisons between the resulting spaces. We use these to show that \(S_e\) is a model for the homotopy colimit of \({\mathscr {C}\text {art}}^\text {op}\)-shaped diagrams of simplicial sets in Sect. 4.2. In Sect. 4.3 we show that applying \(S_e\) to the presheaf associated to a manifold reproduces the homotopy type of the topological space underlying the manifold.
4.1 Comparison results
The right adjoint of \(S_e = \delta ^* \circ \Delta _e^*\) is given as \(R_e = \Delta _{e*} \circ \delta _*\). We start by making this functor more explicit: consider a simplicial set \(K \in {\mathscr {S}\text {et}_{\Delta }}\) and a cartesian space \(c \in {\mathscr {C}\text {art}}\). Since the adjunction \(S_e \dashv R_e\) is simplicial, there are natural isomorphisms
The following lemma is then immediate:
Lemma 4.2
There exist canonical natural isomorphisms
It follows that there exists a natural isomorphism \({\text {ev}}_* \circ R_e \circ {\text {Sing}}\cong {\text {Sing}}\).
Lemma 4.3
There is an isomorphism
natural in both \(T \in {\Delta \mathscr {T}\text {op}}\) and in \(K \in {\mathscr {S}\text {et}_{\Delta }}\).
Proof
Since the adjunction \(|{-}| \dashv {\text {Sing}}\) is simplicial (because \(|{-}|\) preserves finite products), we have binatural isomorphisms
Here we have used that \({\Delta \mathscr {T}\text {op}}\) is cartesian closed and simplicially enriched. \(\square \)
Recall the diffeological topology functor from Definition 2.24.
Lemma 4.4
For every manifold \(M \in {\mathscr {M}\text {fd}}\) there exist morphisms
of simplicial sets and of topological spaces, respectively. These assemble into natural transformations
of functors \({\mathscr {M}\text {fd}}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\) and \({\mathscr {M}\text {fd}}\rightarrow {\Delta \mathscr {T}\text {op}}\), respectively.
Proof
Let \(n \in \mathbb {N}_0\) and consider the set \(\underline{M}(\Delta _e^n) = {\mathscr {M}\text {fd}}(\Delta _e^n, M)\); it is the set of all smooth maps \(\Delta _e^n \rightarrow M\) of manifolds. Recall the morphism \(\iota ^\bullet :|\Delta ^\bullet | \longrightarrow \text {D}\Delta _e^\bullet \) of cosimplicial topological spaces from (3.2). If \(f :\Delta _e^n \rightarrow M\) is any smooth map, then the composition \(f \circ \iota ^n :|\Delta ^n| \rightarrow \text {D}\underline{M}\) is continuous. Here we have used that \(\text {D}\underline{M}\) coincides with the underlying topological space of the manifold M (see Proposition 2.26). This provides a map
Since \(\iota ^\bullet \) is a morphism of cosimplicial topological spaces, and since the maps \(\varphi _{M|n}\) are defined by precomposition by \(\iota ^n\), it readily follows that \(\varphi _{M|n}\) is natural in both \(M \in {\mathscr {M}\text {fd}}\) and  . Thus, we obtain the desired morphism of simplicial sets
. Thus, we obtain the desired morphism of simplicial sets
The composition
then defines the morphism \(\psi _M\), where \(e :|{-}| \circ {\text {Sing}}\overset{\sim }{\longrightarrow }1_{\Delta \mathscr {T}\text {op}}\) is the counit of the Quillen equivalence \(|{-}| \dashv {\text {Sing}}\). \(\square \)
Lemma 4.5
The restrictions of \(\varphi \) and \(\psi \) to \({\mathscr {C}\text {art}}\subset {\mathscr {M}\text {fd}}\) are natural weak equivalences of functors \({\mathscr {C}\text {art}}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\) and \({\mathscr {C}\text {art}}\rightarrow {\Delta \mathscr {T}\text {op}}\), respectively.
Proof
This follows readily from the observation that, for any cartesian space \(c \in {\mathscr {C}\text {art}}\), both \(|S_e {\mathscr {Y}}_c|\) and \(\text {D}({\mathscr {Y}}_c)\) are weakly equivalent to \(* \in {\Delta \mathscr {T}\text {op}}\). Hence, by the two-out-of-three property of weak equivalences any morphism \(|S_e {\mathscr {Y}}_c| \longrightarrow \text {D}({\mathscr {Y}}_c)\) is a weak equivalence. \(\square \)
Proposition 4.6
There exists a natural weak equivalence

Proof
It suffices to consider the projective case since \(\mathscr {H}^{p I}\) and \(\mathscr {H}^{i I}\) have the same weak equivalences (Proposition 2.9). Given a topological space \(T \in {\Delta \mathscr {T}\text {op}}\), by Equation (4.1) and Lemma 4.3 we have
The natural morphisms \(\psi \) from Lemma 4.4 induce a morphism
in \(\mathscr {H}\), which is natural in \(T \in {\Delta \mathscr {T}\text {op}}\).
In order to see that the morphism \({\text {Sing}}(T^{\psi })\) is a weak equivalence in \(\mathscr {H}^{p I}\), we first observe that both S(T) and \(R_e \circ {\text {Sing}}(T)\) are fibrant in \(\mathscr {H}^{p I}\). We have that
Further, the morphism \(\psi _{|*} :|S_e(*)| = * \rightarrow * = \text {D}(*)\) is the identity, so that also the morphism
is the identity. The fact that \(\eta \) is a natural weak equivalence now follows from the fact that the right Quillen equivalence \({\text {ev}}_* :\mathscr {H}^{p I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\) reflects weak equivalences between fibrant objects (which was also the content of Proposition 2.35). \(\square \)
Corollary 4.7
There is a natural weak equivalence

Proof
The functor \(S_e :\mathscr {H}^{p/i\, I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\) is homotopical. Applying it to the natural weak equivalence from Proposition 4.6, we obtain a natural weak equivalence
Let \(e :S_e \circ R_e \longrightarrow 1_{\mathscr {S}\text {et}_{\Delta }}\) denote the counit of the adjunction \(S_e \dashv R_e\). The fact that every object in \({\mathscr {S}\text {et}_{\Delta }}\) is cofibrant, together with the fact that \(S_e \dashv R_e\) is a Quillen equivalence imply that the morphism \(e_{|K} :S_e \circ R_e(K) \longrightarrow K\) is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\) for every fibrant simplicial set K. Since \({\text {Sing}}:{\Delta \mathscr {T}\text {op}}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\) takes values in fibrant simplicial sets, it follows that the composition
is a natural weak equivalence. \(\square \)
Corollary 4.8
Let \(Q^p :\mathscr {H}^{p I} \rightarrow \mathscr {H}^{p I}\) be a cofibrant replacement functor, with associated natural weak equivalence \(q^p :Q^p \rightarrow 1_{\mathscr {H}}\). There is a zig-zag of natural weak equivalences
of functors \(\mathscr {H}^{p I} \longrightarrow {\mathscr {S}\text {et}_{\Delta }}\).
Proof
The left-facing natural transformation is a weak equivalence since \(S_e\) is homotopical. The right-facing morphism is the composition
where \(u :1_{\Delta \mathscr {T}\text {op}}\longrightarrow S \circ Re\) is the unit morphism of the adjunction \(Re \dashv S\). Since this adjunction is a Quillen equivalence and since every object in \({\Delta \mathscr {T}\text {op}}\) is fibrant, it follows that \(u_F :F \rightarrow S \circ Re(F)\) is a weak equivalence for every cofibrant object \(F \in \mathscr {H}^{p I}\). \(\square \)
Proposition 4.10
There exists a zig-zag of natural weak equivalences
of functors \(\mathscr {H}^{p I} \longrightarrow {\Delta \mathscr {T}\text {op}}\). In particular, there exists a natural isomorphism of total left derived functors between homotopy categories

Observe that \(S_e\) and \(|{-}|\) are already homotopical, so that we do not need to precompose them by a cofibrant replacement in order to obtain their total left derived functors.
Proof
We readily obtain a zig-zag as in (4.11) by applying the functor \(|{-}|\) to the zig-zag (4.9) and then postcomposing by the counit \(e :|{-}| \circ {\text {Sing}}\overset{\sim }{\longrightarrow }1_{\Delta \mathscr {T}\text {op}}\). \(\square \)
Remark 4.12
There is an alternative way of obtaining a zig-zag as in (4.11) directly and explicitly, when \(Q^p\) is Dugger’s cofibrant replacement functor for \(\mathscr {H}^p\) [20]. It sends a simplicial presheaf F to the two-sided bar construction
in the notation of [43]. (The superscript indicates in which simplicial category we are forming the bar construction.) Using that Re is simplicial and commutes with colimits, and that there is a natural isomorphism \(Re \circ {\mathscr {Y}}_c \cong \text {D}\underline{c}\) for any cartesian space \(c \in {\mathscr {C}\text {art}}\) (cf. Lemma 2.32), we obtain a canonical isomorphism
Now we use that the morphism \(\psi \) from Lemma 4.4 induces a natural weak equivalence \(\psi :|{-}| \circ S_e \overset{\sim }{\longrightarrow }\text {D}\) of functors \({\mathscr {C}\text {art}}\rightarrow {\Delta \mathscr {T}\text {op}}\) (cf. Lemma 4.5). Since each of the functors \(F :{\mathscr {C}\text {art}}^\text {op}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\) and \(\text {D}, |{-}| \circ S_e :{\mathscr {C}\text {art}}\rightarrow {\Delta \mathscr {T}\text {op}}\) takes values in cofibrant objects, [43, Cor. 5.2.5] implies that \(\psi \) induces a weak equivalence
of functors \(\mathscr {H}\rightarrow {\Delta \mathscr {T}\text {op}}\).
On the other hand, since both \(|{-}|\) and \(S_e\) are left adjoints, we have a natural isomorphism
Now, the morphism \(q^p :Q^p \overset{\sim }{\longrightarrow }1_{\mathscr {H}}\), together with the fact that both \(|{-}|\) and \(S_e\) preserve weak equivalences, yield the claim. \(\triangleleft \)
Remark 4.13
Recall the embedding \(\iota :{\mathscr {D}\text {fg}}\hookrightarrow \mathscr {H}\) of diffeological spaces into simplicial presheaves. By Lemma 2.32, the composition \(Re \circ \iota \) agrees with the functor \(\text {D}:{\mathscr {D}\text {fg}}\rightarrow {\Delta \mathscr {T}\text {op}}\) that sends a diffeological space to its underlying topological space, whose topology is induced by its plots. It is interesting to ask whether the homotopy type of \(\text {D}X\) agrees with that of the smooth singular complex \(S_e \iota (X)\) of X, for any diffeological space \(X \in {\mathscr {D}\text {fg}}\). So far, however, we only see that the homotopy type of \(S_e \iota X\) agrees with the cobar construction
rather than with the underlying topological space \(\text {D}X\) of X. This is in accordance with—and maybe provides some further insight to—results from [10, 39] that the smooth singular complex of a diffeological space X is not in general equivalent to the smooth singular complex of \(\text {D}X\). \(\triangleleft \)
4.2 Homotopy colimits of smooth spaces
We can interpret the functor Re—and because of Proposition 4.10 also the functor \(S_e\)—in the context of the cohesive \(\infty \)-topos \({{\textbf {H}}}\) of presheaves of spaces on \({\mathscr {C}\text {art}}\) as follows (see [44] for more background and [8] for a brief introduction). From the proof of Proposition 4.10 we see that there are canonical weak equivalences
Using the fact that the topological realisation of a bisimplicial set is independent of which simplicial direction one realises first (up to canonical isomorphism), we obtain canonical weak equivalences
Combining this with Proposition 4.10, we obtain
Theorem 4.14
Each of the functors
models the homotopy colimit of diagrams \({\mathscr {C}\text {art}}^\text {op}\rightarrow {\Delta \mathscr {T}\text {op}}\). That is, there is a natural isomorphism between each of these functors and \({\text {hocolim}}_{{\mathscr {C}\text {art}}^\text {op}}\) as functors
It follows that \(S_e\) models the homotopy colimit of diagrams \({\mathscr {C}\text {art}}^\text {op}\longrightarrow {\mathscr {S}\text {et}_{\Delta }}\).
Therefore, each of these functors presents the \(\infty \)-categorical colimit functor for diagrams of spaces indexed by \({\mathscr {C}\text {art}}^\text {op}\). Consequently, on the level of the underlying \(\infty \)-categories they each present left-adjoints to the functor that sends a space to the constant presheaf whose value is that space. This means that both Re and \(S_e\) provide explicit presentations for the left-adjoint \(\Pi \) in the three-fold adjunction which implements the cohesive structure on \({{\textbf {H}}}\) (see [44]). A different argument for the case of \(S_e\) has been given in [4] (see the bottom of p. 2); here we establish a presentation of the \(\infty \)-categorical adjunction \(\Pi \dashv \tilde{\textsf {c}}\) as a Quillen adjunction \(\mathscr {H}^{p/i} \rightleftarrows {\mathscr {S}\text {et}_{\Delta }}\) and a Quillen equivalence \(\mathscr {H}^{p/i\,I} \rightleftarrows {\mathscr {S}\text {et}_{\Delta }}\).
4.3 Recovering homotopy types of manifolds
Recall the fully faithful embedding \({\mathscr {M}\text {fd}}\hookrightarrow \mathscr {H}\), \(M \mapsto \underline{M}\). In this section, we show that, for any manifold M, the smooth singular complex \(S_e \underline{M}\) and the ordinary singular complex \({\text {Sing}}(\text {D}\underline{M})\) of M are canonically weakly equivalent. In fact, this is a well-known and classical result in geometric topology. We nevertheless present this statement and a short proof in a language suited to this paper as a consistency check for the properties of the functor \(S_e\). Classical proofs of this statement can be found, for instance, in [34, Thm. 18.7] and [52, Secs. 5.31, 5.32] (a version with cubes instead of simplices is in [23]).
Theorem 4.15
The natural transformations

introduced in Lemma 4.4 are natural weak equivalences. In particular, the smooth singular complex of \(\underline{M}\) has the same homotopy type as \({\text {Sing}}M\).
Proof
It suffices to prove the claim for \(\varphi \), since \(\psi \) is the composition of \(|\varphi |\) with a weak equivalence in \({\Delta \mathscr {T}\text {op}}\), and \(|{-}|\) preserves and detects weak equivalences. Let \({\mathscr {U}}= \{U_a\}_{a \in A}\) be a differentiably good open covering of M. Then, the canonical morphism \(\pi :{\check{C}}{\mathscr {U}}\rightarrow \underline{M}\) from the Čech nerve of \({\mathscr {U}}\) to \(\underline{M}\) is a weak equivalence in \(\mathscr {H}^{p/i\, \ell }\): the morphism \({\check{C}}{\mathscr {U}}_0 = \coprod _{a \in A} \underline{U}_a \longrightarrow \underline{M}\) is a local epimorphism, or generalised cover (in the sense of [12, p. 7]) with respect to the Grothendieck topology of differentiably good open coverings on \({\mathscr {C}\text {art}}\) [22]. Hence, the claim follows by [12, Cor. A.3]. Therefore, \(\pi \) becomes a weak equivalence under \(S_e\) by Corollaries 2.12 and 3.15.
We can equivalently write

where \({\check{C}}_n {\mathscr {U}}= \coprod _{a_0, \ldots , a_n \in A} U_{a_0 \cdots a_n}\) is the n-th level of the Čech nerve of \({\mathscr {U}}\), and where we view the simplicial presheaf \({\check{C}}{\mathscr {U}}\) as a diagram

of simplicially constant presheaves on \({\mathscr {C}\text {art}}\). We thus arrive at a commutative diagram

in \({\mathscr {S}\text {et}_{\Delta }}\). We have already argued that the left-hand vertical morphism is a weak equivalence. The top horizontal morphism is a weak equivalence as well: for each  , the morphism \(\varphi \) induces a morphism between simplicial sets which are a disjoint union of contractible components. On the level of connected components, \(\varphi \) induces a bijection, and hence is a weak equivalence. Finally, the classical Nerve Theorem (see e.g. [7, 14, 35, 45]) implies that the right-hand vertical morphism is an equivalence as well. \(\square \)
, the morphism \(\varphi \) induces a morphism between simplicial sets which are a disjoint union of contractible components. On the level of connected components, \(\varphi \) induces a bijection, and hence is a weak equivalence. Finally, the classical Nerve Theorem (see e.g. [7, 14, 35, 45]) implies that the right-hand vertical morphism is an equivalence as well. \(\square \)
5 Local fibrant replacement, concordance and mapping spaces
In this section, we present a fibrant replacement functor in the model structures \(\mathscr {H}^{p/i\, I}\). Its construction is motivated by the concordance sheaf construction from [4]. This functor allows us to compute mapping spaces in \(\mathscr {H}^{p/i\, I}\) in Theorem 5.6. We start by presenting the fibrant replacement functor:
Lemma 5.1
Suppose that \(F_0, F_1 \in \mathscr {H}\) and that \(h :F_0 \times \underline{\mathbb {R}} \rightarrow F_1\) is a smooth homotopy between morphisms \(f,g :F_0 \rightarrow F_1\). Then, for any \(G \in \mathscr {H}\), there is a smooth homotopy \(\tilde{h} :G^{F_1} \times \underline{\mathbb {R}} \rightarrow G^{F_0}\) from \(G^f\) to \(G^g :G^{F_1} \rightarrow G^{F_0}\).
Proof
Applying the exponential functor \(G^{(-)}\) to the morphism h, we obtain a morphism
Using the internal-hom adjunction of \(\mathscr {H}\) then yields a morphism \(\tilde{h} = (G^h)^\dashv \in \mathscr {H}(G^{F_1} \times \underline{\mathbb {R}}, G^{F_0})\) with the desired properties. \(\square \)
We consider the following construction: let \(\underline{\Delta }_e^k \in \mathscr {H}\) denote the simplicial presheaf represented by the extended affine simplex \(\Delta _e^k \in {\mathscr {C}\text {art}}\). This provides a functor

Given an object \(F \in \mathscr {H}\), we can compose this functor by the functor \(F^{(-)} :\mathscr {H}\rightarrow \mathscr {H}\), obtaining an object  . Equivalently, we can view this as a bisimplicial presheaf
. Equivalently, we can view this as a bisimplicial presheaf
which we can now compose by the diagonal functor \(\delta ^* :s{\mathscr {S}\text {et}_{\Delta }}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\) to obtain a new simplicial presheaf on \({\mathscr {C}\text {art}}\). Putting everything together, this defines a functor
The collapse morphisms \(\Delta _e^k \rightarrow *\) induce a natural transformation \(\underline{\Delta }_e \rightarrow *\) of functors  (this even consists of I-local equivalences by Proposition 2.10). From this we obtain a natural transformation
(this even consists of I-local equivalences by Proposition 2.10). From this we obtain a natural transformation
Now, let \(R^{p/i} :\mathscr {H}\rightarrow \mathscr {H}\) be a fibrant replacement functor for the projective (resp. injective) model structure, with natural objectwise weak equivalence \(r^{p/i} :1_{\mathscr {H}} \overset{\sim }{\longrightarrow }R^{p/i}\). (Observe, in particular, that a fibrant replacement functor \(R^p\) for the projective model structure can be obtained by postcomposition with a fibrant replacement functor in \({\mathscr {S}\text {et}_{\Delta }}\), i.e. we can use \(R^p(F) = R^{\mathscr {S}\text {et}_{\Delta }}\circ F\) for \(F \in \mathscr {H}\). An explicit model for an injective fibrant replacement functor is given in Appendix A.) We define functors
for the projective and the injective model structure, respectively. We define the natural transformation
Proposition 5.2
The functors \({\text {Cc}}^{p/i}\), together with the natural morphisms \({\text {cc}}^{p/i}\) provide a functorial fibrant replacement in \(\mathscr {H}^{p/i\, I}\).
Proof
First, we show that \({\text {Cc}}^{p/i} F\) is indeed fibrant in the I-local model structure \(\mathscr {H}^{p/i\, I}\), for every \(F \in \mathscr {H}\). By construction, \({\text {Cc}}^{p/i} F\) is a fibrant object in \(\mathscr {H}^{p/i}\). It thus remains to show that it is \(\mathbb {R}\)-local. For any \(c \in {\mathscr {C}\text {art}}\), we have that
By Lemma 5.1, the smooth homotopy equivalence \({\mathscr {Y}}_c \rightarrow *\) induces a smooth homotopy equivalence \(F \rightarrow F^{{\mathscr {Y}}_c}\), which is a weak equivalence in \(\mathscr {H}^{p/i\, I}\) by Corollary 3.16. Since \(r^{p/i}\) is a natural weak equivalence of functors valued in \(\mathscr {H}^{p/i}\), its component
is an objectwise weak equivalence. Consequently, for every \(c \in {\mathscr {C}\text {art}}\), we have a commutative square

whose vertical morphisms are induced from the collapse morphism \(c \rightarrow *\). It follows that \({\text {Cc}}^{p/i}F\) is \(\mathbb {R}\)-local and hence a fibrant object in \(\mathscr {H}^{p/i\, I}\).
Finally, we need to show that the morphism \(\gamma _{|F} :F \longrightarrow \delta ^* \circ F^{\underline{\Delta }_e}\), induced by the collapse \(\Delta _e \rightarrow *\), is a weak equivalence in \(\mathscr {H}^{p/i\, I}\). Since the functor \(S_e :\mathscr {H}^{p/i\, I} \rightarrow {\mathscr {S}\text {et}_{\Delta }}\) preserves as well as reflects weak equivalences, that is equivalent to showing that the induced morphism
is a weak equivalence of simplicial sets. More explicitly, \(S_e(\gamma _{|F})\) is the morphism
induced by collapsing the extended simplices \(\Delta _e\) without the tilde. Note that we have only added the tilde in order to keep track of which diagonal functor refers to which copy of \(\Delta _e\). We have canonical isomorphisms
and we know from the first part of this proof that the morphism
is a weak equivalence, for every \(k \in \mathbb {N}_0\). This induces a (levelwise) weak equivalence of bisimplicial sets
which under \(\delta ^*\) maps to the morphism \(S_e(\gamma _{|F})\). Since the diagonal functor \(\delta ^* :s{\mathscr {S}\text {et}_{\Delta }}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\) is homotopical, we obtain that \(S_e(\gamma _{|F})\), and thus also \(\gamma _{|F}\), is indeed a weak equivalence. \(\square \)
Corollary 5.3
Mapping spaces in \(\mathscr {H}^{p/i\, I}\) can be computed (up to isomorphism in \(\text {h}{\mathscr {S}\text {et}_{\Delta }}\)) as the simplicially enriched hom spaces
where \(Q^p\) is a cofibrant replacement functor for the projective model structure \(\mathscr {H}^p\).
Definition 5.5
Given an object \(F \in \mathscr {H}\), we call \({\text {Cc}}^{p/i} F\) its (projective/injective) derived concordance sheaf. For \(G \in \mathscr {H}\) we refer to the spaces in (5.4) as the spaces of derived concordances of morphisms from F to G.
We can apply these insights to describe the mapping spaces in the model categories \(\mathscr {H}^{p/i\, I}\). In particular, given any \(G \in \mathscr {H}\), part (3) of the following theorem shows that the derived sections of the derived concordance sheaf of G (in the sense of Definition 5.5) on manifolds are represented by maps from the space underlying M to the smooth singular complex of G.
Theorem 5.6
There are natural isomorphisms in \(\text {h}{\mathscr {S}\text {et}_{\Delta }}\) as follows:
-
(1)
For \(F,G \in \mathscr {H}\), we have
$$\begin{aligned} \text {Map}_{\mathscr {S}\text {et}_{\Delta }}(S_e F, S_e G) \cong \text {Map}_{\mathscr {H}^{p/i\, I}}(F,G)\,. \end{aligned}$$ -
(2)
For \(F,G \in \mathscr {H}\), we have
$$\begin{aligned} \text {Map}_{\Delta \mathscr {T}\text {op}}(|S_e F|, |S_e G|) \cong \text {Map}_{\mathscr {H}^{p/i\, I}}(F,G)\,. \end{aligned}$$ -
(3)
For any manifold M and \(G \in \mathscr {H}\), we have
$$\begin{aligned} \text {Map}_{\Delta \mathscr {T}\text {op}}(M, |S_e G|) \cong \text {Map}_{\mathscr {H}^{p/i\, I}}(\underline{M},G)\,. \end{aligned}$$
Proof
It suffices to consider one of the model structures by Proposition 2.9 and the fact that the mapping spaces in a model category depend only on the underlying relative category (see before Corollary A.11). For claim (1), we consider the injective model structure. Using that every object in \(\mathscr {H}^{i I}\) is cofibrant, we have the following isomorphisms in \(\text {h}{\mathscr {S}\text {et}_{\Delta }}\):
The first isomorphism is merely the fact that \({\mathscr {S}\text {et}_{\Delta }}\) is a simplicial model category in which every object is cofibrant. In the second isomorphism, we use the fact that \(S_e \dashv R_e\) is a simplicial adjunction. To see the third isomorphism, we use the weak equivalence \({\text {cc}}^i_{|G} :G \overset{\sim }{\longrightarrow }{\text {Cc}}^i(G)\) from Proposition 5.2. Since both \(S_e\) and \(R^{\mathscr {S}\text {et}_{\Delta }}\) are homotopical functors, and since \(R_e\) preserves fibrant objects, the morphism \(R_e R^{\mathscr {S}\text {et}_{\Delta }}S_e ({\text {cc}}^i_{|G})\) is a weak equivalence between fibrant objects in \(\mathscr {H}^{i I}\), which is thus preserved by \(\underline{\mathscr {H}}(F, -)\). The fourth isomorphism stems from the fact that \(S_e \dashv R_e\) is a Quillen equivalence, so that the canonical natural transformation \(1_{\mathscr {H}} \longrightarrow R_e R^{\mathscr {S}\text {et}_{\Delta }}S_e\) is a weak equivalence in \(\mathscr {H}^{i I}\) on every cofibrant object—that is, it is a weak equivalence on every object, since all objects in \(\mathscr {H}^{i I}\) are cofibrant. Further, its component at the object \({\text {Cc}}^i(G)\) is a weak equivalence between fibrant objects in \(\mathscr {H}^{i I}\), which is again preserved by \(\underline{\mathscr {H}}(F, -)\). The final isomorphism directly follows from the insight that \({\text {Cc}}^i\) is a fibrant replacement functor for \(\mathscr {H}^{i I}\) (Proposition 5.2).
Claim (2) then follows from the fact that every object in \({\Delta \mathscr {T}\text {op}}\) is fibrant and that every object of \({\mathscr {S}\text {et}_{\Delta }}\) is cofibrant: if \(K,L \in {\mathscr {S}\text {et}_{\Delta }}\), then there are canonical isomorphisms in \(\text {h}{\mathscr {S}\text {et}_{\Delta }}\)
Claim (3) then follows from combining part (2) with Theorem 4.15. \(\square \)
We can now give a direct proof of the relation between model categories announced in Remark 3.17: we characterise the homotopy theory induced on \(\mathscr {H}\) by the smooth singular complex functor \(S_e\):
Theorem 5.7
Let \(W_{\mathscr {S}\text {et}_{\Delta }}\) denote the class of weak equivalences in \({\mathscr {S}\text {et}_{\Delta }}\), and let \(S_e^{-1}(W_{\mathscr {S}\text {et}_{\Delta }})\) denote the class of morphisms in \(\mathscr {H}\) whose image under \(S_e\) is in \(W_{\mathscr {S}\text {et}_{\Delta }}\). There is an identity of model categories
Proof
We set
The model categories \(\mathscr {H}^{p/i\, I}\) and \({\mathscr {M}}^{p/i}\) have the same cofibrations, since they are left Bousfield localisations of the same model category. (Here we use either the projective or the injective model structure on both sides.) By Theorem 2.11 it now suffices to show that they have the same fibrant objects. Corollary 3.15 implies that \(I \subset S_e^{-1}(W_{\mathscr {S}\text {et}_{\Delta }})\); thus, any fibrant object in \({\mathscr {M}}^{p/i}\) is also fibrant in \(\mathscr {H}^{p/i\, I}\).
To see that any fibrant object of \(\mathscr {H}^{p/i\, I}\) is also fibrant in \({\mathscr {M}}^{p/i}\), consider a fibrant object \(G \in \mathscr {H}^{p/i\, I}\) and a morphism \(f :F_0 \rightarrow F_1\) in \(S_e^{-1}(W_{\mathscr {S}\text {et}_{\Delta }})\). By Theorem 5.6, we have a commutative diagram

in \(\text {h}{\mathscr {S}\text {et}_{\Delta }}\). By assumption on f, the morphism \(S_e f\) is a weak equivalence in \({\mathscr {S}\text {et}_{\Delta }}\). Hence, it induces a weak equivalence on mapping spaces; that is, the bottom morphism in the diagram is an isomorphism in \(\text {h}{\mathscr {S}\text {et}_{\Delta }}\). From that, it follows that also the top morphism is an isomorphism in \(\text {h}{\mathscr {S}\text {et}_{\Delta }}\), which implies that G is \(S_e^{-1}(W_{\mathscr {S}\text {et}_{\Delta }})\)-local, and therefore fibrant in \({\mathscr {M}}^{p/i}\). \(\square \)
Remark 5.8
Part (3) of Theorem 5.6 is related to recent results by Berwick-Evans, Boavida de Brito and Pavlov from [4]: in that paper, the authors work with the category \(\widetilde{\mathscr {H}}\) of simplicial presheaves on \({\mathscr {M}\text {fd}}\). Given \(\widetilde{G} \in \widetilde{\mathscr {H}}\), they consider the concordance sheaf
where the exponential is taken in \(\widetilde{\mathscr {H}}\). The inclusion functor \(\iota :{\mathscr {C}\text {art}}\hookrightarrow {\mathscr {M}\text {fd}}\) induces a homotopy right Kan extension \({\text {hoRan}}_\iota ' :\mathscr {H}\rightarrow \widetilde{\mathscr {H}}\) (see Appendix B for details). Explicitly, working with projective model structures, we can write
for any \(M \in {\mathscr {M}\text {fd}}\), where \(Q' :\mathscr {H}^p \rightarrow \mathscr {H}^p\) is the cofibrant replacement functor introduced in Appendix A. The functor \({\text {hoRan}}_\iota ' :\mathscr {H}^{p \ell } \rightarrow \widetilde{\mathscr {H}}^{p \ell }\) is a right Quillen functor, where on the target side we consider the Čech localisation with respect to open coverings—this is a consequence of [9, Prop. 3.16, Thm. 3.18]. It provides a concrete way of comparing sheaves on \({\mathscr {C}\text {art}}\) to sheaves on \({\mathscr {M}\text {fd}}\): the functor
is a right Quillen equivalence by Theorem B.8.
We can now compare the derived concordance sheaves from Definition 5.5 to the concordance sheaf construction (5.9) from [4]: let \(F \in \mathscr {H}\) be any simplicial presheaf on \({\mathscr {C}\text {art}}\). On the one hand, we have
and on the other hand, we have
Given that \({\text {hoRan}}_\iota '(F)\) is a sheaf on \({\mathscr {M}\text {fd}}\), it now follows from [4, Thm. 1.1, Thm. 1.2] that \({\text {B}}{\text {hoRan}}_\iota '(F)\) is a sheaf on \({\mathscr {M}\text {fd}}\) as well. Then, Proposition B.6 implies that \({\text {hoRan}}_\iota '({\text {Cc}}^p F)\) and \({\text {B}}{\text {hoRan}}_\iota '(F)\) are isomorphic in \(\text {h}\widetilde{\mathscr {H}}^{p \ell }\) if and only if their images under the restriction functor \(\iota ^* :\widetilde{\mathscr {H}}^{p \ell } \rightarrow \mathscr {H}^{p \ell }\) are isomorphic in \(\text {h}\mathscr {H}^{p \ell }\).
If \(M = c\) is a cartesian space, we readily obtain a natural weak equivalence
and we further obtain natural weak equivalences
The first weak equivalence uses that \(\Delta _e^k\) is a cartesian space, for each \(k \in \mathbb {N}_0\), so that \(c \times \Delta _e^k\) is representable in \(\mathscr {H}\), and the last morphism arises from postcomposing with a fibrant replacement functor in \({\mathscr {S}\text {et}_{\Delta }}\). This establishes a natural zig-zag of weak equivalences between \({\text {hoRan}}_\iota '({\text {Cc}}^p F)\) and \({\text {B}}{\text {hoRan}}_\iota '(F)\). Note that the results [4, Thm. 1.1, Thm. 1.2] enter crucially in the construction of this zig-zag because we use the fact that \({\text {B}}{\text {hoRan}}_\iota '(F)\) is a sheaf on \({\mathscr {M}\text {fd}}\). \(\triangleleft \)
Remark 5.10
We outline an alternative proof of Theorem 5.6, based on Proposition 5.2 and Theorem 2.20 (which we recall goes back to [18]). Let \(F, G \in \mathscr {H}\), and let \(Q :\mathscr {H}^p \rightarrow \mathscr {H}^p\) denote a cofibrant replacement functor. In the homotopy category \(\text {h}{\mathscr {S}\text {et}_{\Delta }}\) of spaces, we have natural isomorphisms
In the second isomorphism, we have used that \({\text {Cc}}^p G\) is essentially constant and that \({\text {Cc}}^p G(*) = R^{\mathscr {S}\text {et}_{\Delta }}\circ S_e G\). The third isomorphism arises from the Quillen adjunction \({\text {colim}}: \mathscr {H}^p \rightleftarrows {\mathscr {S}\text {et}_{\Delta }}: \tilde{\textsf {c}}\), and the fourth isomorphism stems from fact that \({\text {colim}}\circ Q\) models the homotopy colimit. Finally, the fifth isomorphism arises from our observation at the end of Sect. 4 that \(S_e F\) is a model for the homotopy colimit of the diagram \(F :{\mathscr {C}\text {art}}^\text {op}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\). Parts (2) and (3) of Theorem 5.6 then follow as in our proof above. \(\triangleleft \)
Notes
We thank the referee for making us aware of this work.
See the two discussion threads https://nforum.ncatlab.org/discussion/6816/the-shape-of-function-objects and https://nforum.ncatlab.org/discussion/11361/shape-via-cohesive-path-groupoid; we thank the anonymous referee for pointing these out to us.
References
Amabel, A., Debray, A., Haine, P.J.: Differential cohomology: Categories, characteristic classes, and connections. arXiv:2109.12250v1
Barwick, C.: \((\infty ,n)\)-Cat as a closed model category. PhD thesis, University of Pennsilvania, (2005). https://repository.upenn.edu/dissertations/AAI3165639/
Barwick, C.: On left and right model categories and left and right Bousfield localizations. Homol. Homotopy Appl. 12(2), 245–320 (2010). arXiv:0708.2067v2
Berwick-Evans, D., Boavida de Brito, P., Pavlov, D.: Classifying spaces of infinity-sheaves. arXiv:1912.10544v1
Beke, T.: Sheafifiable homotopy model categories. Math. Proc. Camb. Philos. Soc. 129(3), 447–475 (2000). arXiv:math/0102087v1
Bunke, U., Nikolaus, T., Völkl, M.: Differential cohomology theories as sheaves of spectra. J. Homotopy Relat. Struct. 11(1), 1–66 (2016). arXiv:1311.3188v1
Borsuk, K.: On the imbedding of systems of compacta in simplicial complexes. Fund. Math. 35, 217–234 (1948). https://doi.org/10.4064/fm-35-1-217-234
Bunk, S.: Principal \(\infty \)-bundles and smooth string group models. Math. Ann. arXiv:2008.12263v3 (to appear)
Bunk, S.: Sheaves of higher categories on generalised spaces. arXiv:2003.00592v2
Christensen, J.D., Sinnamon, G., Wu, E.: The \(D\)-topology for diffeological spaces. Pac. J. Math. 272(1), 87–110 (2014). arXiv:1302.2935v4
Christensen, J.D., Wu, E.: The homotopy theory of diffeological spaces. N. Y. J. Math. 20, 1269–1303 (2014). arXiv:1311.6394v4
Dugger, D., Hollander, S., Isaksen, D.C.: Hypercovers and simplicial presheaves. Math. Proc. Camb. Philos. Soc. 136(1), 9–51 (2004). arXiv:math/0205027v2
Dwyer, W.G., Hirschhorn, P.S., Kan, D.M., Smith, J.H.: Homotopy Limit Functors on Model Categories and Homotopical Categories, vol. 113. Mathematical Surveys and Monographs. American Mathematical Society, Providence (2004). https://doi.org/10.1090/surv/113
Dugger, D., Isaksen, D.C.: Topological hypercovers and \(\mathbb{A}^1\)-realizations. Math. Z. 246(4), 667–689 (2004). arXiv:math/0111287v1
Dwyer, W.G., Kan, D.M.: Function complexes in homotopical algebra. Topology 19(4), 427–440 (1980)
Dundas, B.I., Levine, M., Østvær, P.A., Röndigs, O., Voevodsky, V.: Motivic Homotopy Theory. Universitext. Springer, Berlin, 2007. Lectures from the Summer School held in Nordfjordeid, August (2002). https://doi.org/10.1007/978-3-540-45897-5
Dugger, D.: Notes on delta-generated spaces. https://pages.uoregon.edu/ddugger/delta.html
Dugger, D.: Sheaves and homotopy theory. http://math.mit.edu/~dspivak/files/cech.pdf
Dugger, D.: Combinatorial model categories have presentations. Adv. Math. 164(1), 177–201 (2001). arXiv:math/0007068v1
Dugger, Daniel: Universal homotopy theories. Adv. Math. 164(1), 144–176 (2001). arXiv:math/0007070v1
Fajstrup, L., Rosický, J.: A convenient category for directed homotopy. Theory Appl. Categ. 21(1), 7–20 (2008). arXiv:0708.3937v1
Fiorenza, D., Schreiber, U., Stasheff, J.: Čech cocycles for differential characteristic classes: an \(\infty \)-Lie theoretic construction. Adv. Theor. Math. Phys. 16(1), 149–250 (2012). arXiv:1011.4735v1
Fulton, W.: Algebraic Topology, vol. 153. Graduate Texts in Mathematics. Springer, New York (1995) (a first course)
Goerss, P.G., Jardine, J.F.: Simplicial Homotopy Theory. Modern Birkhäuser Classics. Birkhäuser Verlag, Basel (2009) (reprint of the 1999 edition)
Galatius, S., Tillmann, U., Madsen, I., Weiss, M.: The homotopy type of the cobordism category. Acta Math. 202(2), 195–239 (2009). arXiv:math/0605249v3
Haraguchi, T.: On model structure for coreflective subcategories of a model category. Math. J. Okayama Univ. 57, 79–84 (2015)
Hirschhorn, P.S.: Model Categories and Their Localizations, vol. 99. Mathematical Surveys and Monographs. American Mathematical Society, Providence (2003). https://doi.org/10.1090/surv/099
Horel, G.: A model structure on internal categories in simplicial sets. Theory Appl. Categ. 30, 704–750 (2015). arXiv:1403.6873v5
Hovey, M.: Model Categories, vol. 63. Mathematical Surveys and Monographs. American Mathematical Society, Providence (1999). https://doi.org/10.1090/surv/063
Herrmann, P., Strunk, F.: Enriched simplicial presheaves and the motivic homotopy category. J. Pure Appl. Algebra 215(7), 1663–1668 (2011). arXiv:1007.3153v1
Iglesias-Zemmour, P.: Diffeology, vol. 185. Mathematical Surveys and Monographs. American Mathematical Society, Providence (2013). https://doi.org/10.1090/surv/185
Jardine, J.F.: Local Homotopy Theory. Springer Monographs in Mathematics. Springer, New York (2015)
Joyal, A.: The theory of quasicategories and its applications. https://mat.uab.cat/~kock/crm/hocat/advanced-course/Quadern45-2.pdf
Lee, J.M.: Introduction to smooth manifolds, 2nd ed., vol. 218. Graduate Texts in Mathematics. Springer, New York (2013)
Leray, J.: L’anneau spectral et l’anneau filtré d’homologie d’un espace localement compact et d’une application continue. J. Math. Pures Appl. (9), 29, 1–80, 81–139, (1950)
Lurie, J.: Higher Topos Theory, vol. 170. Annals of Mathematics Studies. Princeton University Press, Princeton (2009). https://www.math.ias.edu/~lurie/papers/HTT.pdf
Morel, F., Voevodsky, V.: A\(^1\)-homotopy theory of schemes. Inst. Hautes Études Sci. Publ. Math. 90, 45–143 (2001), (1999). https://doi.org/10.1007/BF02698831
Madsen, I., Weiss, M.: The stable moduli space of Riemann surfaces: Mumford’s conjecture. Ann. Math. (2) 165(3), 843–941 (2007). arXiv:math/0212321v3
Oh, Y.-G., Tanaka, H.L.: Smooth approximation for classifying spaces of diffeomorphism groups. arXiv:2003.06033v3
Quillen, D.G.: Homotopical Algebra. Lecture Notes in Mathematics, No. 43. Springer, Berlin, New York (1967)
Rezk, C.: A model for the homotopy theory of homotopy theory. Trans. Am. Math. Soc. 353(3), 973–1007 (2001). arXiv:math/9811037v3
Rezk, C.: A Cartesian presentation of weak \(n\)-categories. Geom. Topol. 14(1), 521–571 (2010). arXiv:0901.3602v3
Riehl, E.: Categorical Homotopy Theory, vol. 24. New Mathematical Monographs. Cambridge University Press, Cambridge (2014). https://math.jhu.edu/~eriehl/cathtpy.pdf
Schreiber, U.: Differential cohomology in a cohesive \(\infty \)-topos. https://ncatlab.org/schreiber/files/dcct170811.pdf
Segal, G.: Categories and cohomology theories. Topology 13, 293–312 (1974). https://doi.org/10.1016/0040-9383(74)90022-6
Shulman, M.: Homotopy limits and colimits and enriched homotopy theory. arXiv:math/0610194v3
Souriau, J.-M.: Groupes différentiels. In: Differential Geometrical Methods in Mathematical Physics (Proc. Conf., Aix-en-Provence/Salamanca, 1979), vol. 836. Lecture Notes in Math., pp. 91–128. Springer, Berlin, New York (1980)
Sati, H., Schreiber, U.: Equivariant principal infinity-bundles. arXiv:2112.13654v3
Shimakawa, K., Yoshida, K., Haraguchi, T.: Homology and cohomology via enriched bifunctors. arXiv:1010.3336v1
Voevodsky, V.: A\(^1\)-homotopy theory. In: Proceedings of the International Congress of Mathematicians, vol. I (Berlin, 1998), pp. 579–604 (1998). https://eudml.org/doc/226397
Vogt, R.M.: Convenient categories of topological spaces for homotopy theory. Arch. Math. (Basel) 22, 545–555 (1971). https://doi.org/10.1007/BF01222616
Warner, F.W.: Foundations of differentiable Manifolds and Lie Groups, vol. 94. Graduate Texts in Mathematics. Springer, New York, Berlin (1983). Corrected reprint of the (1971) edition
Acknowledgements
The author is grateful to Birgit Richter for her encouragement to carry out this project. Further, the author would like to thank Walker Stern and Lukas Müller for numerous discussions, as well as Dan Christensen, Enxin Wu, Daniel Berwick-Evans, Pedro Boavida de Brito and Dmitri Pavlov for insightful comments on an earlier version of this paper. Finally, the author is grateful to the anonymous referee, whose very careful reading and detailed comments improved this paper notably. The author was partially supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC 2121 “Quantum Universe”—390833306.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jim Stasheff.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
An injective fibrant replacement of simplicial presheaves
From the definition of the projective and the injective model structure on \(\mathscr {H}\), it follows directly that there is a Quillen equivalence

Both of the functors in this adjunction are the identity on \(\mathscr {H}\). Here, we will construct a Quillen equivalence in the opposite direction, i.e.

We start by defining the functor \(Q'\). Its construction is not specific to simplicial presheaves on \({\mathscr {C}\text {art}}\), but works for simplicial presheaves over any small category. Thus, let \(\mathscr {C}\) be a small category, let \({\mathscr {K}}\) denote the category of simplicial presheaves on \(\mathscr {C}\), and let \({\mathscr {Y}}:\mathscr {C}\rightarrow {\mathscr {K}}\) denote the Yoneda embedding. We denote the projective and the injective model structures on \({\mathscr {K}}\) by \({\mathscr {K}}^p\) and by \({\mathscr {K}}^i\), respectively. The conventional two-sided simplicial bar construction provides a functor [43, Sec. 4.2]

Lemma A.1
The functor \(B_\bullet ((-), \mathscr {C}, {\mathscr {Y}})\) sends injective cofibrations in \({\mathscr {K}}\) to injective cofibrations in  . That is, if \(f :F \rightarrow G\) is an objectwise cofibration of simplicial presheaves on \(\mathscr {C}\), then \(B_n (f, \mathscr {C}, {\mathscr {Y}})\) is a projective cofibration of simplicial presheaves, for each \(n \in \mathbb {N}_0\).
. That is, if \(f :F \rightarrow G\) is an objectwise cofibration of simplicial presheaves on \(\mathscr {C}\), then \(B_n (f, \mathscr {C}, {\mathscr {Y}})\) is a projective cofibration of simplicial presheaves, for each \(n \in \mathbb {N}_0\).
Proof
We have that
Observing that \({\mathscr {Y}}_c \in {\mathscr {K}}^p\) is cofibrant for every \(c \in \mathscr {C}\) and recalling that \({\mathscr {K}}^p\) is a simplicial model category, we see that, in each part of the coproduct, the functor
is a left Quillen functor. \(\square \)
In order to obtain Dugger’s cofibrant replacement functor Q, one needs to take the diagonal (objectwise) of the bisimplicial presheaf \(B_\bullet ((-),\mathscr {C}, {\mathscr {Y}})\):
It is not evident to us whether taking the diagonal of a bisimplicial presheaf maps injective cofibrations in  to projective cofibrations in \({\mathscr {K}}\). That is the motivation for constructing the functor \(Q'\) below.
to projective cofibrations in \({\mathscr {K}}\). That is the motivation for constructing the functor \(Q'\) below.
Let \(\mathscr {I}\) be a small category, \({\mathscr {V}}\) a symmetric monoidal category, and \({\mathscr {M}}\) a model category category enriched, tensored and cotensored over \({\mathscr {V}}\) (i.e. a model \({\mathscr {V}}\)-category in the terminology of [3]). Following the notation in [43, Sec. 4.1], we let
denote the functor tensor product and the functor hom, respectively. Let \({\mathscr {C}\text {at}}_s\) denote the (1-)category of small categories, and let  denote the functor that sends
denote the functor that sends  to the slice category
to the slice category  , and let N denote the nerve functor. We now define the functor
, and let N denote the nerve functor. We now define the functor

Lemma A.4
The functor \(Q' :{\mathscr {K}}^i \rightarrow {\mathscr {K}}^p\) preserves cofibrations.
Proof
We view the functor tensor product in the definition of \(Q'\) as

The functor tensor product is a left Quillen bifunctor when endowing the two source categories with any of the pairs of model structures (projective, injective), (Reedy, Reedy), or (injective, projective) [43, Thms. 11.5.9, 14.3.1]. Further, the functor  is projectively cofibrant [27, Prop. 14.8.8]. (Note that it is then also Reedy cofibrant.) Consequently, the functor
is projectively cofibrant [27, Prop. 14.8.8]. (Note that it is then also Reedy cofibrant.) Consequently, the functor

is left Quillen with respect to the injective model structure on  (and hence also with respect to the Reedy model structure). We can write \(Q'\) as the composition
(and hence also with respect to the Reedy model structure). We can write \(Q'\) as the composition

The model category of simplicial diagrams in the middle carries the injective model structure. We have shown in Lemma A.1 that the first functor preserves cofibrations, and it follows from our arguments above that the second functor preserves cofibrations as well. \(\square \)
Next, we are going to employ the Bousfield-Kan map to show that \(Q'\) provides a cofibrant replacement functor on \({\mathscr {K}}^p\). The Bousfield-Kan map is a morphism

of cosimplicial simplicial sets. We will use the following two statements:
Proposition A.5
[27, Prop. 18.7.2] The Bousfield-Kan map is a Reedy weak equivalence between Reedy cofibrant cosimplicial simplicial sets.
Proposition A.6
For any \(F \in {\mathscr {K}}\), the simplicial object in \({\mathscr {K}}\) given as \(B_\bullet (F,\mathscr {C}, {\mathscr {Y}})\) is Reedy cofibrant.
Proof
This follows directly from [43, Rmk. 5.2.2], applied to the functor \({\mathscr {Y}}:\mathscr {C}\rightarrow {\mathscr {K}}^p\). \(\square \)
We now consider the induced natural transformation

By Proposition A.6, the functor

is a left Quillen functor for every \(F \in {\mathscr {K}}\). It then follows from Proposition A.5 and the arguments in the proof of Proposition A.4 that the natural transformation (A.7) is a natural weak equivalence of functors \({\mathscr {K}}\rightarrow {\mathscr {K}}^p\). Finally, we use that the functor \(B((-),\mathscr {C},{\mathscr {Y}})\) agrees with Dugger’s cofibrant replacement functor \(Q^p\) for \({\mathscr {K}}^p\) from [20]. In particular, it comes with a natural weak equivalence \(q^p :Q^p \rightarrow 1_{{\mathscr {K}}}\). Composing \(q^p\) with the morphism (A.7), we obtain a natural weak equivalence \(q' :Q' \rightarrow 1_{{\mathscr {K}}}\). Putting everything together, we have proven
Proposition A.8
The functor \(Q'\) from (A.3), together with the natural weak equivalence \(q'\), provides a cofibrant replacement functor for \({\mathscr {K}}^p\). In particular, \(Q'\) preserves objectwise weak equivalences.
Finally, we observe that \(Q'\) has a right adjoint, which is explicitly given by

where \({\mathscr {Y}}^{(-)} :\mathscr {C}^\text {op}\rightarrow {\mathscr {C}\text {at}}(\mathscr {C}, {\mathscr {S}\text {et}_{\Delta }})\) denotes the co-Yoneda embedding of \(\mathscr {C}\).
Theorem A.10
The functors \(Q'\) and \(R'\) satisfy the following properties:
-
(1)
The adjunction \(Q' \dashv R'\) is a Quillen equivalence
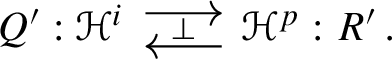
-
(2)
There is a natural transformation \(r' :1_{{\mathscr {K}}} \rightarrow R'\) such that \(r'_{|G} :G \rightarrow R'G\) is a weak equivalence in \({\mathscr {K}}^i\) for every projectively fibrant \(G \in {\mathscr {K}}\).
-
(3)
Let \(R^{\mathscr {S}\text {et}_{\Delta }}\) be a fibrant replacement functor for simplicial sets. Then, \(G \mapsto R' (R^{\mathscr {S}\text {et}_{\Delta }}\circ G)\) is a fibrant replacement functor on \({\mathscr {K}}^i\).
Proof
Ad (1): Proposition A.8, together with the observation that \(Q'\) is a left adjoint, readily implies that \(Q'\) is a left Quillen functor. The fact that this is a Quillen equivalence follows from the existence of the natural weak equivalence \(q' :Q' \overset{\sim }{\longrightarrow }1_{{\mathscr {K}}}\). Formally, this implies that the composition of \(Q'\) by the left Quillen equivalence \(1_{{\mathscr {K}}} :{\mathscr {K}}^p \rightarrow {\mathscr {K}}^i\) is weakly equivalent to the identity functor on \({\mathscr {K}}\). Thus, the statement follows from the two-out-of-three property of Quillen equivalences [29].
Ad (2): Let
be the natural isomorphism that establishes the adjunction \(Q' \dashv R'\). We define \(r' :1_{{\mathscr {K}}} \rightarrow R'\) to be the image under \(\tau \) of the natural transformation \(q'\). Now consider the weak equivalence \(q'_{|G} :Q'G \rightarrow G\), for \(G \in {\mathscr {K}}^p\) fibrant. By part (1) and since each object in \({\mathscr {K}}^i\) is cofibrant, the morphism \(r'_{|G} :G \rightarrow R'G\) is a weak equivalence.
Ad (3): Let \(R^{\mathscr {S}\text {et}_{\Delta }}\) be a fibrant replacement functor in \({\mathscr {S}\text {et}_{\Delta }}\), with associated natural weak equivalence \(r^{\mathscr {S}\text {et}_{\Delta }}:1_{\mathscr {S}\text {et}_{\Delta }}\overset{\sim }{\longrightarrow }R^{\mathscr {S}\text {et}_{\Delta }}\). Let \(G \in {\mathscr {K}}\) be arbitrary and consider the composition

The first morphism is an objectwise weak equivalence by definition. Since \(R^{\mathscr {S}\text {et}_{\Delta }}\circ G\) is projectively fibrant, the second morphism is a weak equivalence as well by part (2). \(\square \)
Finally, we recall that the mapping spaces in a model category depend only on the weak equivalences, i.e. their homotopy types are determined completely by the underlying relative category. This was famously proven in [15, Prop. 4.4]; the simpler case of simplicial model categories—which applies directly to the present situation—is in [15, Cor. 4.7]. In particular, we record the following direct consequence for reference:
Proposition A.11
Let F, G be any two objects in \({\mathscr {K}}\). There is a canonical isomorphism in the homotopy category \(\text {h}{\mathscr {S}\text {et}_{\Delta }}\) of spaces between the mapping spaces of the projective and the injective model structures
Sheaves on manifolds and sheaves on cartesian spaces
This appendix is devoted to the comparison of two localisations: on the one hand, we consider the localisation \(\mathscr {H}^{p \ell }\) of the projective model structure \(\mathscr {H}^p\) of simplicial presheaves on cartesian spaces at the Čech nerves of differentiably good open coverings (see Section 2.1). On the other hand, we have the localisation \(\widetilde{\mathscr {H}}^{p \ell }\) of the projective model structure \(\widetilde{\mathscr {H}}^p\) of simplicial presheaves on manifolds at the Čech nerves of open coverings. (The same arguments also apply to the localisation of \(\widetilde{\mathscr {H}}^p\) at the Čech nerves of surjective submersions.)
We will compare these localisations by means of the functors
where \(\iota :{\mathscr {C}\text {art}}\hookrightarrow {\mathscr {M}\text {fd}}\) is the canonical inclusion, and where \(Q :\mathscr {H}^p \rightarrow \mathscr {H}^p\) is Dugger’s cofibrant replacement functor for the projective model structure on simplicial presheaves (A.2). Further, \(Q' \dashv R'\) is the Quillen equivalence from Theorem A.10. The natural transformation (A.7) induces a natural transformation \(\eta :{\text {hoRan}}_\iota \longrightarrow {\text {hoRan}}_\iota '\) whose component \(\eta _{|F}\) on every fibrant object \(F \in \mathscr {H}^p\) is a projective weak equivalence.
The functor \({\text {hoRan}}_\iota :\mathscr {H}^p \rightarrow \widetilde{\mathscr {H}}^p\) is a right Quillen functor with left adjoint \(Q \circ \iota ^*\), and this Quillen adjunction descends to a Quillen adjunction on Čech localisations,

by the universal property of left Bousfield localisations. Analogously, \({\text {hoRan}}_\iota ' :\mathscr {H}^p \rightarrow \widetilde{\mathscr {H}}^p\) is a right Quillen functor (since \(Q'\) is homotopical and valued in projectively cofibrant simplicial presheaves). Further, the natural transformation \(\eta :{\text {hoRan}}_\iota \longrightarrow {\text {hoRan}}_\iota '\) establishes that \({\text {hoRan}}_\iota '\) maps local objects in \(\mathscr {H}^{p \ell }\) to local objects in \(\widetilde{\mathscr {H}}^{p \ell }\), and hence that we also have a Quillen adjunction

Note that we can also write the right adjoint as
with \(R' :\mathscr {H}\rightarrow \mathscr {H}\) defined as in (A.9), and where \(\iota _*\) is the right Kan extension along \(\iota \).
Lemma B.1
The derived counit of the Quillen adjunction \(Q' \circ \iota ^* \dashv {\text {hoRan}}_\iota '\) is a projective weak equivalence on every fibrant \(F \in \mathscr {H}^p\).
Proof
Let \(\widetilde{Q} :\widetilde{\mathscr {H}}^p \rightarrow \widetilde{\mathscr {H}}^p\) be a cofibrant replacement functor with associated natural weak equivalence \(\widetilde{q} :\widetilde{Q} \overset{\sim }{\longrightarrow }1_{\widetilde{\mathscr {H}}}\). Consider a fibrant object \(F \in \mathscr {H}^p\) and the composition

nnnnnwhich is the derived counit. The first morphism is given by \((Q' \circ \iota ^*)\widetilde{q}_{|\iota _* \circ R'(F)}\). It is a weak equivalence in \(\mathscr {H}^p\) because \(\widetilde{q}_{|\iota _* \circ R'(F)}\) is a projective weak equivalence and \(\iota ^* :\widetilde{\mathscr {H}}^p \rightarrow \mathscr {H}^p\) is homotopical, as is \(Q'\). The second morphism is the counit of the adjunction \(\iota ^* \dashv \iota _*\), which is an isomorphism by the Yoneda Lemma. The third morphism is a weak equivalence by Theorem A.10 and the fact that every object in \(\mathscr {H}^i\) is cofibrant. \(\square \)
It follows that the total derived functor \(\mathbb {R}{\text {hoRan}}_\iota ' :\text {h}\mathscr {H}^p \rightarrow \text {h}\widetilde{\mathscr {H}}^p\) is fully faithful, and hence that also \(\mathbb {R}{\text {hoRan}}_\iota ' :\text {h}\mathscr {H}^{p \ell } \rightarrow \text {h}\widetilde{\mathscr {H}}^{p \ell }\) is fully faithful.
Next, we show that \(\mathbb {R}{\text {hoRan}}_\iota '\) is essentially surjective. We start by recalling that, for any open covering \({\mathscr {U}}= \{U_a\}_{a \in A}\) of a manifold M, the induced Čech nerve \({\check{C}}{\mathscr {U}}\rightarrow \underline{M}\) is a weak equivalence in both \(\mathscr {H}^{p \ell }\) and \(\widetilde{\mathscr {H}}^{p \ell }\) (this follows directly from [12, Cor. A.3]). If \({\mathscr {U}}\) is even a differentiably good open covering of M (i.e. each finite intersection of patches is either empty or a cartesian space), then \({\check{C}}{\mathscr {U}}\) is levelwise a coproduct of representables in \(\mathscr {H}\). Hence, it is cofibrant in \(\mathscr {H}^{p \ell }\).
Suppose that \(G \in \widetilde{\mathscr {H}}^{p \ell }\) is fibrant. Given a manifold M with a differentiably good open covering \({\mathscr {U}}\), we have weak equivalences
In this sense, the value of a sheaf G on manifolds is determined by its values on cartesian spaces. However, the above weak equivalence is not functorial in M, so we need to improve on (B.2).
For \(M \in {\mathscr {M}\text {fd}}\), let \({\text {Cov}}(M)\) denote the category whose objects are open covering \({\mathscr {U}}= \{U_a\}_{a \in A}\) of M. Given another open covering \({\mathscr {V}}\) of M there is a unique morphism \({\mathscr {V}}\rightarrow {\mathscr {U}}\) precisely if \({\mathscr {V}}\) refines \({\mathscr {U}}\). Let \({\text {GCov}}(M)\) denote the full subcategory of \({\text {Cov}}(M)\) on the differentiably good open coverings. Note that \({\text {Cov}}(M)\) is cofiltered since every pair \(({\mathscr {U}},{\mathscr {V}})\) of open coverings has a common refinement \({\mathscr {U}}\times _M {\mathscr {V}}\). Moreover, any open covering of M has a differentiably good refinement [22, App. A], which implies that \({\text {GCov}}(M)\) is cofiltered and that the canonical inclusion \(j_M :{\text {GCov}}(M) \hookrightarrow {\text {Cov}}(M)\) is homotopy final, since for any \({\mathscr {U}}\in {\text {Cov}}(M)\) the slice category \(j/{\mathscr {U}}\) is cofiltered as well.
Given \(G \in \widetilde{\mathscr {H}}\), we consider the diagrams in simplicial sets
Since \({\text {Cov}}(M)^\text {op}\) is filtered and \({\mathscr {S}\text {et}_{\Delta }}\) is combinatorial, the ordinary colimits of these diagrams model their homotopy colimits [19, Prop. 7.3], so that we obtain a morphism
(The right-hand side of (B.3) is Grothendieck’s Plus Construction, applied to M and G.) If \(G \in \widetilde{\mathscr {H}}^{p \ell }\) is fibrant, then the morphism in (B.3) is a weak equivalence, for each manifold \(M \in {\mathscr {M}\text {fd}}\). Since \(j_M^\text {op}:{\text {GCov}}(M)^\text {op}\hookrightarrow {\text {Cov}}(M)^\text {op}\) is cofinal, we further obtain a canonical isomorphism
If \({\mathscr {U}}\in {\text {GCov}}(M)\), then \({\check{C}}{\mathscr {U}}\) is levelwise a coproduct of presheaves represented by cartesian spaces. Hence, there is a further canonical isomorphism
where \(\iota :{\mathscr {C}\text {art}}\hookrightarrow {\mathscr {M}\text {fd}}\) is the inclusion. Thus, for any \(G \in \widetilde{\mathscr {H}}\) and any \(M \in {\mathscr {M}\text {fd}}\) we obtain a morphism
which is natural in G and which is a weak equivalence whenever \(G \in \widetilde{\mathscr {H}}^{p \ell }\) is fibrant.
Next we show that \(\gamma _{G,M}\) is also natural in M. Let \(f :M \rightarrow N\) be a smooth map. This induces a functor \(f^* :{\text {Cov}}(N) \rightarrow {\text {Cov}}(M)\), acting via \(f^*(\{U_a\}_{a \in A}) = \{f^{-1}(U_a)\}_{a \in A}\). This establishes the assignment \(M \mapsto {\text {Cov}}(M)\) as a (strict) functor \({\text {Cov}}:{\mathscr {M}\text {fd}}^\text {op}\rightarrow {\mathscr {C}\text {at}}_s\) to the (large) category of small categories. Given an open covering \({\mathscr {U}}\) of N, the map f induces a canonical morphism \(\widehat{f} :{\check{C}}(f^*{\mathscr {U}}) \rightarrow {\check{C}}{\mathscr {U}}\) in \(\widetilde{\mathscr {H}}\). This induces a natural transformation

Further, recall that for any composition of functors \(\mathscr {I}\overset{F}{\longrightarrow }\ \mathscr {J}\overset{D}{\longrightarrow }\ \mathscr {C}\) there is a canonical morphism \({\text {colim}}(D \circ F) \rightarrow {\text {colim}}(D)\). Thus, we have a canonical morphism
Combining this morphism with the natural transformation \(\varphi \) yields a morphism
in \({\mathscr {S}\text {et}_{\Delta }}\) which is compatible with composition of smooth maps of manifolds. Finally, we use the isomorphisms (B.4) to define the top morphism in the diagram

It follows that the assignment
defines a functor \({\mathscr {M}\text {fd}}^\text {op}\rightarrow {\mathscr {S}\text {et}_{\Delta }}\). That is, we obtain a functor
coming with a natural transformation \(\gamma :1_{\widetilde{\mathscr {H}}} \rightarrow {\text {Pl}}\) which is an objectwise weak equivalence on every fibrant \(G \in \widetilde{\mathscr {H}}^{p \ell }\). In particular, we have shown:
Proposition B.6
Let \(G,G' \in \widetilde{\mathscr {H}}^{p \ell }\) be fibrant. A morphism \(g :G \rightarrow G'\) is a weak equivalence in \(\widetilde{\mathscr {H}}^{p \ell }\) if and only if \(\iota ^*g :\iota ^*G \rightarrow \iota ^*G'\) is a weak equivalence in \(\mathscr {H}^{p \ell }\).
Note that for \(G,G' \in \widetilde{\mathscr {H}}^{p \ell }\) fibrant, a morphism \(g :G \rightarrow G'\) is a weak equivalence in \(\widetilde{\mathscr {H}}^{p \ell }\) precisely if it is an objectwise equivalence (since both G and \(G'\) are local objects), and analogously \(\iota ^*g :\iota ^*G \rightarrow \iota ^*G'\) is a weak equivalence if and only if it is an objectwise equivalence (since \(\iota ^* :\widetilde{\mathscr {H}}^{p \ell } \rightarrow \mathscr {H}^{p \ell }\) preserves fibrant objects).
Lemma B.7
The functor \(\mathbb {R}{\text {hoRan}}_\iota ' :\text {h}\mathscr {H}^{p \ell } \longrightarrow \text {h}\widetilde{\mathscr {H}}^{p \ell }\) is essentially surjective.
Proof
Let \(G \in \widetilde{\mathscr {H}}^{p \ell }\) be fibrant. We show that there is a zig-zag of weak equivalences in \(\widetilde{\mathscr {H}}^{p \ell }\) linking G to \({\text {hoRan}}_\iota ' \circ \iota ^*(G)\). First, since G and \({\text {hoRan}}_\iota ' \circ \iota ^*(G)\) are both sheaves on \({\mathscr {M}\text {fd}}\), there are local weak equivalences
where \({\text {Pl}}:\widetilde{\mathscr {H}}^{p \ell } \rightarrow \widetilde{\mathscr {H}}^{p \ell }\) is the functor from (B.5). Further, for \(c \in {\mathscr {C}\text {art}}\) we have that
so the natural weak equivalence \(Q' \overset{\sim }{\longrightarrow }1_{\mathscr {H}}\) induces a projective weak equivalence
For any manifold M and any differentiably good open covering \({\mathscr {U}}\) of M, this induces a weak equivalence
Since \({\text {GCov}}(M)^\text {op}\) is filtered, this yields a weak equivalence \({\text {Pl}}G \overset{\sim }{\longrightarrow }{\text {Pl}}({\text {hoRan}}_\iota ' \circ \iota ^*(G))\), thus establishing the desired zig-zag of weak equivalences. \(\square \)
By Lemmas B.1 and B.7, the total derived functor \(\mathbb {R}{\text {hoRan}}_\iota ' :\text {h}\mathscr {H}^{p \ell } \rightarrow \text {h}\widetilde{\mathscr {H}}^{p \ell }\) is an equivalence.
Theorem B.8
The following adjunction is a Quillen equivalence:

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bunk, S. The \(\mathbb {R}\)-local homotopy theory of smooth spaces. J. Homotopy Relat. Struct. 17, 593–650 (2022). https://doi.org/10.1007/s40062-022-00318-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40062-022-00318-7



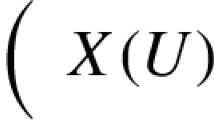

 :
: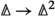
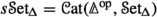 of bisimplicial sets. Our convention is always to write a bisimplicial set as a functor
of bisimplicial sets. Our convention is always to write a bisimplicial set as a functor 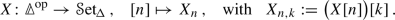
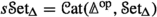 as endowed with the injective model structure. Recall that this coincides with the Reedy model structure [
as endowed with the injective model structure. Recall that this coincides with the Reedy model structure [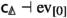 is a Quillen adjunction
is a Quillen adjunction