Quasi-categories vs. Segal spaces: Cartesian edition

Abstract

We prove that four different ways of defining Cartesian fibrations and the Cartesian model structure are all Quillen equivalent:

• 1. On marked simplicial sets (due to Lurie [31]),

• 2. On bisimplicial spaces (due to deBrito [12]),

• 3. On bisimplicial sets,

• 4. On marked simplicial spaces.

The main way to prove these equivalences is by using the Quillen equivalences between quasi-categories and complete Segal spaces as defined by Joyal–Tierney and the straightening construction due to Lurie.

1 Introduction

1.1 Functors via fibrations

For a given category $\mathscr {C}$, we are often interested in studying pseudo-functors of the form

$$\begin{aligned} P: \mathscr {C}^{op} \rightarrow \mathscr {C}\text {at}\end{aligned}$$

where $\mathscr {C}\text {at}$ is the (large) category of (small) categories. Such functors commonly arise in algebraic geometry (such as moduli problems [1]), topos theory (such as internal toposes [26]), algebraic topology (such as moduli stacks in chromatic homotopy [15]), ... .

In certain mathematical situations, so-called derived or homotopical mathematics, the definition of a category is too strict and we need to work with a weaker notion of a category in which the usual axioms of a category only hold up to suitably compatible equivalences or “homotopies" [21]. The study of such categories is now usually called the theory of $(\infty ,1)$-categories [7].

Continuing our analogy with classical categories, the study of homotopical mathematics, such as derived algebraic geometry [30], higher topos theory [31], ... , again requires us to study $(\infty ,1)$-functors

$$\begin{aligned} P: \mathscr {C}^{op} \rightarrow \mathscr {C}\text {at}_{(\infty ,1)}, \end{aligned}$$

however, unlike the classical case, this is quite challenging and often not feasible. Indeed, because of the higher coherence conditions, any such functor P requires an infinite tower of data, which usually prevents us from giving explicit descriptions.

Fortunately, there is an alternative approach towards such functors in the context of categories: fibrations. A functor $p: \mathscr {D}\rightarrow \mathscr {C}$ is called a Grothendieck fibration if every morphism in $\mathscr {C}$, with specified lift of the target in $\mathscr {D}$, can be lifted to a p-Cartesian morphisms in $\mathscr {D}$.

Here, a morphism $f: x \rightarrow y$ in $\mathscr {D}$ is p-Cartesian if the induced commutative square

is a pseudo-pullback of categories.

Using this definition of fibration, Grothendieck [2] proved following equivalence between pseudo-functors and Grothendieck fibrations,

$$\begin{aligned} \displaystyle \int _\mathscr {C}: \mathrm {Fun}(\mathscr {C}^{op}, \mathscr {C}\text {at}) \xrightarrow { \ \simeq \ } \mathscr {G}\mathrm {roth}\mathscr {F}\mathrm {ib}_\mathscr {C}, \end{aligned}$$

now commonly called the Grothendieck construction, thus giving us a way to translate between Grothendieck fibrations and pseudo-functors valued in categories.

The fibrational approach is far more amenable to $(\infty ,1)$-categorical techniques and thus can be generalized in a straightforward manner. This was done by Lurie [31]. Using quasi-categories, which are simplicial sets that model $(\infty ,1)$-categories [11, 27, 28], he defined Cartesian fibrations as inner fibrations of simplicial sets that have sufficient p-Cartesian lifts.

Following a long tradition in homotopy theory, he then proceeded to define a model structure [35] such that the fibrant objects were precisely the Cartesian fibrations over a fixed simplicial set S. However, he did not define the model structure on the category of simplicial sets over S, but rather on the category of marked simplicial sets over S, which are simplicial sets with a chosen subset of the set of 1-simplices. Hence, despite the fact that the definition of a Cartesian fibration required no markings, the markings were a crucial aspect of its model structure.¹

Using this model structure, aptly named the Cartesian model structure, he then proves a Quillen equivalence [31, Theorem 3.2.0.1]

which is simply a technical correspondence between Cartesian fibrations and functors valued in $(\infty ,1)$-categories, thus giving us a concrete way to transition between those, generalizing the Grothendieck construction from categories to $(\infty ,1)$-categories.

In the subsequent years, several authors have studied Cartesian fibrations. For example, Riehl and Verity study Cartesian fibrations in the context of an $\infty$-cosmos, which is a formal approach to $(\infty ,1)$-categories [42] motivated by formal category theory. Another example is the work by Ayala and Francis, who study the quasi-category of Cartesian fibrations from the perspective of exponentiable fibrations [5]. It should be noted, however, that neither approach results in a new model category for Cartesian fibrations. Rather they use the fact that the definition of $\infty$-cosmoi or quasi-categories are less strict to study Cartesian fibrations directly, without having to take an external approach.

1.2 Cartesian fibrations via complete Segal objects

In this paper we propose an alternative approach towards Cartesian fibrations via complete Segal objects (rather than marked simplicial objects) which results in a new a model category of Cartesian fibrations. In order to understand this different approach it is necessary to understand complete Segal spaces, right fibrations and how they can interact.

A complete Segal space [40] is a simplicial space

that satisfies three sets of conditions (the Reedy, Segal and completeness conditions). These conditions imply that complete Segal spaces are another model of $(\infty ,1)$-categories and in particular equivalent to quasi-categories [29] and can in fact be seen as the standard model [45].

The benefit of complete Segal spaces is that the conditions can all be expressed via certain finite limit diagrams [41]. Hence, we can easily generalize a complete Segal space to a complete Segal object in any category (or model category or $(\infty ,1)$-category) with finite limits. Using our intuition from complete Segal spaces, we expect a complete Segal object in a category to play the role of an internal $(\infty ,1)$-category.² So, in particular, a complete Segal object in the category of space-valued presheaves is precisely a presheaf valued in complete Segal spaces i.e. $(\infty ,1)$-categories.

The discussion in the previous paragraph motivates us to study fibrations that correspond to presheaves valued in spaces. As spaces are special kinds of $(\infty ,1)$-categories, we could simply think of them as special kinds of Cartesian fibrations. However, it turns out there is a direct approach as well: right fibrations [27, 28]. A right fibration is a map of simplicial sets that satisfies the right lifting condition with respect to squares

where $n \ge 0$, $0 < i \le n$. Unlike Cartesian fibrations we can in fact endow the category of simplicial sets over a fixed simplicial set with a model structure, the contravariant model structure, such that the fibrant objects are precisely the right fibrations. It was first proven by Lurie [31] (and later many other authors [23, 24, 44]), that this model structure is Quillen equivalent to presheaves valued in spaces. Moreover, we can give an analogous definition of right fibrations and contravariant model structure in the context of simplicial spaces in a way that is Quillen equivalent to the contravariant model structure for simplicial sets [12, 37].

Combining the two previous paragraphs, we should expect that a complete Segal object in right fibrations, which has the form

recovers functors valued in $(\infty ,1)$-categories. This intuition is in fact correct and the goal of this paper is to make this statement precise and prove it.

Combining our previous observation, we are thus studying two ways of constructing Cartesian fibrations, the marked approach and the complete Segal approach, using two models of $(\infty ,1)$-categories, quasi-categories and complete Segal spaces, giving us a total of four characterizations of Cartesian fibrations, which we can depict as follows:

	Marked approach	Complete Segal object approach
Quasi-categories
Complete Segal spaces

The marked approach using quasi-categories is the original approach due to Lurie. The complete Segal approach using complete Segal spaces is studied on its own in [38], and directly results in the complete Segal approach using quasi-categories, which we cover in Sect. 1.6. This leaves us with the marked approach using complete Segal spaces, which we study in Sect. 2. Finally, we show all four model structures are indeed Quillen equivalent in Sect. 3.

1.3 Why the complete Segal object approach?

Given that we already have a working definition of Cartesian fibrations using marked simplicial objects, why present an alternative approach using complete Segal objects?

Studying Cartesian fibrations via right fibrations: One set of applications follows from the key observation that in the complete Segal approach Cartesian fibrations are a direct generalization of right fibrations and thus, their properties can be directly deduced from right fibrations.

• Generalized Cartesian fibrations: We can relax the complete Segal conditions used to define Cartesian fibrations to define generalized Cartesian fibrations, that can be used to study presheaves valued in various other localizations of simplicial spaces, such as Segal spaces [38].

• Invariance of Cartesian fibrations: One important result about the Cartesian model structure is the fact that it is invariant under categorical equivalences, meaning base change by a categorical equivalence gives us a Quillen equivalence. This is proven in [31, Proposition 3.3.1.1] using the fact that the Cartesian model structure is Quillen equivalent to a presheaf category. We can use a similar equivalence between the contravariant model structure and a presheaf category to similarly deduce that right fibrations are invariant under categorical equivalences. However, in this case there is also an alternative proof, which uses the combinatorics of the contravariant model structure [23]. Using the complete Segal object approach to Cartesian fibrations we can generalize that proof immediately from right fibrations to Cartesian fibrations without having to translate to presheaf categories.

• Grothendieck Construction of Cartesian Fibrations: Another example where we can exploit the connection to right fibrations is the Grothendieck construction. In [31], Lurie first proves the equivalence between right fibrations and space-valued presheaves. He then wants to generalize that to an equivalence between Cartesian fibrations and $(\infty ,1)$-category-valued presheaves, but cannot directly do so and thus needs several detailed and complicated proofs. On the other hand, in the complete Segal object approach to Cartesian fibrations every proof of the equivalence between right fibrations and space valued presheaves immediately generalizes to a new proof of the Grothendieck fibration for Cartesian fibrations.

• Grothendieck Construction over 1-Categories: One particular instance of the previous point is the study of Cartesian fibrations over ordinary categories. In [23], the authors give a Grothendieck construction for right fibrations very much along the lines of the classical Grothendieck construction for categories (also known as the category of elements). They then prove that this gives us a Quillen equivalence. Again, using the complete Segal approach, we can realize that using the category of elements we can construct an equivalence between Cartesian fibrations over categories and presheaves. This construction is much simpler than the general unstraightening construction and even simpler than the specific one given over categories in [31, 3.2.5].

Studying Fibrations of $(\infty ,n)$-Categories: The way we generalized 1-categories to $(\infty ,1)$-categories, we can generalize strict n-categories to $(\infty ,n)$-categories [8]. Moreover, similar to the $(\infty ,1)$-categorical case, the study of functors

$$\begin{aligned} P: \mathscr {C}^{op} \rightarrow \mathscr {C}\text {at}_{(\infty ,n)}, \end{aligned}$$

where $\mathscr {C}$ is an $(\infty ,n)$-category, is quite a challenge, as we encounter the same problems with homotopy coherence. Thus we again would like to develop an appropriate theory of fibrations.

However, the $(\infty ,n)$-categorical case faces far more challenges than the $(\infty ,1)$-categorical case. First of all, similar to the $(\infty ,1)$-categories, there are several models of $(\infty ,n)$-categories: $\varTheta _n$-spaces [41], $\varTheta _n$-sets [4], n-fold complete Segal spaces [6], complicial sets [46], comical sets [14], ... . However, it is not known whether these models are in fact equivalent (except for $\varTheta _n$-sets, $\varTheta _n$-spaces and n-fold complete Segal spaces [4, 9, 10]). Second, we don’t have a general definition of fibrations for any of these models of $(\infty ,n)$-categories.³

Hence, unlike for $(\infty ,1)$-categories, we cannot just focus on one model, prove all the relevant results, and then translate the results, via a web of Quillen equivalences. If we need a theory of fibrations for a certain model, then we really need to study it on its noted.

Finally, we also cannot just ignore certain models, with the hope that future results will facilitate translating results from one model to another. First of all it is not certain that such equivalences of models will be developed anytime soon (even the study of strict n-categories is quite challenging) and second of all most models already have concrete applications in other branches of mathematics. For example n-fold complete Segal spaces are currently the primary method for the study of topological field theories [13, 33]. Or alternatively 2-complicial sets (or alternatively 2-comical sets) have found applications in the study of derived algebraic geometry [17, 18], as explained in [14, Page 2].

As $\varTheta _n$-spaces and n-fold complete Segal spaces are directly generalizations of complete Segal spaces, we would expect that a complete Segal approach towards Cartesian fibrations can be a powerful tool in the study of their fibrations.

1.4 Where to go from here?

There are several interesting question about the connection between the various Cartesian model structures that remains unexplored:

• 1. The equivalence between the Cartesian model structures relies on proving that all four are equivalent to various functor categories. It is not clear whether we can construct a direct equivalence between marked simplicial objects and bisimplicial objects that induces an equivalence between the associated Cartesian model structures.

• 2. Along the same lines, one of the benefits of using the marked simplicial approach is that it is reasonably easy to see that Cartesian fibrations are themselves categorical fibrations. We would like to generalize this result and, for example, prove that generalized Cartesian fibrations that characterize functors valued in Segal spaces are always Segal fibrations [38]. However, the current Quillen equivalences do not allow us to draw such a conclusion. Answering this question might rely on first having a better way to translate between marked simplicial objects and bisimplicial objects.

• 3. Assuming we can construct a direct equivalence between marked simplicial sets and bisimplicial sets, a final question would be whether we can effectively use that to deduce all the results about Cartesian fibrations as originally proven in [31, Chapter 3], hence significantly simplifying the results.

1.5 Relation to other work

This paper is the second part of a three-paper series which introduces the bisimplicial approach to Cartesian fibrations:

• 1. Cartesian Fibrations of Complete Segal Spaces [38]

• 2. Quasi-Categories vs. Segal Spaces: Cartesian Edition

• 3. Cartesian Fibrations and Representability [36]

In particular, the first paper includes a detailed analysis of the Cartesian model structure on bisimplicial spaces, which we only review here (Sect. 1.6). The third paper gives an application of the bisimplicial approach to the study of representable Cartesian fibrations.

1.6 Notations

Given that the goal is to prove existence of several Quillen equivalences, we use many different model structures (some times on the same category). Thus, in order to avoid any confusion, we will denote every category with its associated model structure. In order to help the reader, here is a list of all relevant model structures (except the four Cartesian model structures already mentioned), the underlying category, along with the abbreviation and a reference to their definition:

Model structure	Category(ies)	Abbreviation	Reference
Joyal Model Structure	$s\mathscr {S}\text {et}$	Joy	Theorem 1.12
Complete Segal space model structure	$s\mathscr {S}$	CSS	Theorem 1.16
Complete Segal Object Model Structure	$s\fancyscript{M}$	CSO	Theorem 1.19
Contravariant model structure	$s\mathscr {S}_{/X}$	contra	Theorem 1.26
Contravariant model structure	$s\mathscr {S}\text {et}_{/S}$	contra	Theorem 1.28
localized unmarked Reedy Model Structure	$s\mathscr {S}^+$	$un^+Ree_\fancyscript{L}$	Proposition 2.19
unmarked CSS Model Structure	$s\mathscr {S}^+$	$un^+CSS$	Corollary 2.21
marked CSS Model Structure	$s\mathscr {S}^+$	$CSS^+$	Theorem 2.25

2 Review of relevant concepts

In this section we review some important concepts and establish necessary notation.

2.1 A Plethora of simplicial objects

Let $\varDelta$ be the simplex category with object posets $[n] = \{ 0,1,...,n \}$ and morphisms maps of posets. We will use a variety of simplicial objects, i.e. functors $X: \varDelta ^{op} \rightarrow \mathscr {C}$ and thus need to distinguish them carefully, based on the value of the simplicial objects.

Simplicial Sets/Spaces: We will use two terminologies for functors $X: \varDelta ^{op} \rightarrow \mathscr {S}\text {et}$:

• It is a space if it is an object in the category of simplicial sets with the Kan model structure. In that case the category of spaces is denote $\mathscr {S}$.

• It is a simplicial set if it is an object in the category of simplicial sets with any other model structure (such as Joyal, contravariant, ...). In that case the category of simplicial sets is denoted by $s\mathscr {S}\text {et}$.

We will use following notation regarding simplicial sets/spaces:

• 1. $\varDelta [n]$ denotes the simplicial set representing [n] i.e. $\varDelta [n]_k = \mathrm {Hom}_{\varDelta }([k], [n])$.

• 2. $\partial \varDelta [n]$ denotes the boundary of $\varDelta [n]$ i.e. the largest sub-simplicial set which does not include $id_{[n]}: [n] \rightarrow [n]$. Similarly $\Lambda [n]_l$ denotes the largest simplicial set in $\varDelta [n]$ which does not include $l^{th}$ face.

• 3. Let I[l] be the category with l objects and one unique isomorphisms between any two objects. Then we denote the nerve of I[l] as J[l]. It is a Kan fibrant replacement of $\varDelta [l]$ and comes with an inclusion $\varDelta [l] \rightarrowtail J[l]$, which is a Kan equivalence.

Bisimplicial sets/simplicial spaces: Similar to above we will use two terminologies for functors $X: \varDelta ^{op} \times \varDelta ^{op} \rightarrow \mathscr {S}\text {et}$:

• It is a simplicial space if it is an object in the category of bisimplicial sets with the Reedy model structure or any localization thereof. In that case the category of simplicial spaces is denote $s\mathscr {S}$.

• It is a bisimplicial set if it is an object in the category of bisimplicial sets with any other model structure (such as Reedy contravariant, ...). In that case the category of bisimplicial sets is denoted by $ss\mathscr {S}\text {et}$.

We will use following notation convention for simplicial spaces.

• 1. Denote F(n) to be the simplicial space defined as

  $$\begin{aligned} F(n)_{kl} = \mathrm {Hom}_{\varDelta }([k],[n]). \end{aligned}$$

  Similarly, we define the simplicial space $\varDelta [l]$ as

  $$\begin{aligned} \varDelta [n]_{kl} = \mathrm {Hom}_{\varDelta }([l,[n]) \end{aligned}$$

  Note, $F(n) \times \varDelta [n]$ generate the category of simplicial spaces.

• 3. Let E(n) be denote the simplicial space defined as $E(n)_{kl}= J[n]_k$. In particular E(1) is also known as the walking isomorphism.

• 4. We embed the category of spaces inside the category of simplicial spaces as constant simplicial spaces (i.e. the simplicial spaces S such that $S_n = S_0$ for all n and all simplicial operator maps are identities).

• 5. $\partial F(n)$ denotes the boundary of F(n). Similarly $L(n)_l$ denotes the largest simplicial space in F(n) which lacks the $l^{th}$ face.

• 6. The category $s\mathscr {S}$ is enriched over spaces

  $$\begin{aligned} \mathrm {Map}_{s\mathscr {S}}(X,Y)_n = \mathrm {Hom}_{s\mathscr {S}}(X \times \varDelta [n], Y). \end{aligned}$$

• 7. The category $s\mathscr {S}$ is also enriched over itself:

  $$\begin{aligned} (Y^X)_{kn} = \mathrm {Hom}_{s\mathscr {S}}(X \times F(k) \times \varDelta [n], Y). \end{aligned}$$

• 8. By the Yoneda lemma, for a simplicial space X we have a bijection of spaces

  $$\begin{aligned} X_n \cong \mathrm {Map}_{s\mathscr {S}}(F(n),X). \end{aligned}$$

Bisimplicial spaces: We also use functors $X:\varDelta ^{op} \times \varDelta ^{op} \times \varDelta ^{op} \rightarrow \mathscr {S}\text {et}$, which we call bisimplicial space and denote by $ss\mathscr {S}$.

2.2 Diagrammatic model structures

In this section we review some of the underlying model structures that we can define on the categories defined in Sect. 1.1.

Kan Model Structure: The Kan model structure is one of the first model structures defined and can already be found in [35]. For another detailed account of the Kan model structure see [20].

Theorem 1.1

There is a unique simplicial, combinatorial, proper model structure on $\mathscr {S}$, called the Kan model structure and denoted $\mathscr {S}^{Kan}$ characterized as follows:

• 1. A map is a cofibration if it is a monomorphism.

• 2. A map is a fibration if satisfies the lifting right lifting property with respect to horns $\Lambda [n]_i \rightarrow \varDelta [n]$.

• 3. A map is a weak equivalence if it is homotopy equivalence. (its geometric realization is an equivalence of topological spaces).

Reedy Model Structure for Simplicial Objects: Let $\mathscr {C}^\fancyscript{M}$ be a model category with model structure $\fancyscript{M}$. Then we can define a new model structure on the category of simplicial objects $\mathrm {Fun}(\varDelta ^{op}, \mathscr {C}) = s\mathscr {C}$. This model structure exists for a wide range of model categories, however, here we will focus on the case of interest to us. It was originally constructed by Reedy [39], however we will use [25] as our primary reference.

Theorem 1.2

[25, Theorem 15.3.4, Proposition 15.6.3] Let $\mathscr {C}^\fancyscript{M}$ be a combinatorial, simplicial, left proper model structure such that the cofibrations are monomorphisms. Then there exists a simplicial, combinatorial, left proper model structure on simplicial objects in $\mathscr {C}$, which we call the Reedy model structure and denote $s\mathscr {C}^{Ree_\fancyscript{M}}$, which has following characteristics:

• 1. A map $p: Y \rightarrow X$ is a Reedy cofibration if it is a monomorphism.

• 2. A map $p:Y \rightarrow X$ is a Reedy weak equivalence if it is level-wise a weak equivalence in $\mathscr {C}^\fancyscript{M}$.

• 3. A map $p:Y \rightarrow X$ is a Reedy fibration if for every $n \ge 0$ the induced map

  $$\begin{aligned} Y_n \rightarrow \mathrm {M}_nY \times _{\mathrm {M}_nX} X_n \end{aligned}$$

  is a fibration in $\mathscr {C}^\fancyscript{M}$. Here $\mathrm {M}_n$ is the n-th matching object [25, Definition 15.2.5].

Remark 1.3

If $\mathscr {C}^\fancyscript{M}= \mathscr {S}^{Kan}$, then the n-th matching object of a simplicial space X is given by the space $\mathrm {M}_nX= \mathrm {Map}_{s\mathscr {S}}(\partial F(n), X)$ [25, Proposition 15.6.15].

Notice the construction is invariant under Quillen equivalences.

Lemma 1.4

[25, Proposition 15.4.1] Let

be a Quillen equivalence between model categories. Then the induced adjunction

is a Quillen equivalence as well.

Projective model structure for functor categories The existence of the Reedy model structure relied on the fact that $\varDelta$ is a Reedy category and so the Reedy model structure cannot be applied to any functor category $\mathrm {Fun}(\mathscr {C},\mathscr {D})$. Fortunately, under mild assumptions on a model category, we can construct the projective model structure.

Theorem 1.5

[25, Theorem 11.6.1, Theorem 11.7.3] Let $\mathscr {C}$ be a small category and $\mathscr {D}^\fancyscript{M}$ a combinatorial, simplicial, left proper model category. Then there exists a unique left proper, simplicial, combinatorial model structure on the functor category, denoted $\mathrm {Fun}(\mathscr {C},\mathscr {D}^\fancyscript{M})^{proj}$ and called the projective model structure, such that

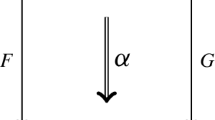
• 1. A map $\alpha : F \rightarrow G$ is a projective fibration if for all objects c in $\mathscr {C}$ the map $\alpha _c: F(c) \rightarrow G(c)$ is a fibration in $\mathscr {D}^\fancyscript{M}$.

• 2. A map $\alpha : F \rightarrow G$ is a projective weak equivalence if for all objects c the map $\alpha _c: F(c) \rightarrow G(c)$ is a weak equivalence in $\mathscr {D}^\fancyscript{M}$.

Similar to the Reedy model structure the projective model structure is also invariant.

Lemma 1.6

[25, Theorem 11.6.5] Let

be a Quillen equivalence between combinatorial simplicial left proper model categories and let $\mathscr {C}$ be a small category. Then the induced adjunction

is a Quillen equivalence as well.

2.3 Constructing new model structures

In this subsection we review several important (and technical) results that help us construct new model structures.

One very common technique is known as Bousfield localization.

Theorem 1.7

Let $\mathscr {C}^\fancyscript{M}$ be a category with a left proper, combinatorial, simplicial model structure $\fancyscript{M}$. Moreover, let $\fancyscript{L}$ be a set of cofibrations in $\mathscr {C}^\fancyscript{M}$. There exists a unique cofibrantly generated, left proper, simplicial model category structure on $\mathscr {C}$, called the $\fancyscript{L}$-localized model structure and denoted $\mathscr {C}^{\fancyscript{M}_\fancyscript{L}}$ with the following properties:

• 1. A morphism $Y \rightarrow Z$ is a cofibration in $\mathscr {C}^{\fancyscript{M}_\fancyscript{L}}$ if it is a cofibration in $\mathscr {C}^\fancyscript{M}$.

• 2. An object W is fibrant (also called $\fancyscript{L}$-local) if it is fibrant in $\mathscr {C}^\fancyscript{M}$ and for every morphism $f: A \rightarrow B$ in $\fancyscript{L}$, the induced map

  $$\begin{aligned} \mathrm {Map}_\mathscr {C}(B, W) \rightarrow \mathrm {Map}_\mathscr {C}(A, W) \end{aligned}$$

  is a Kan equivalence.

• 3. A map $Y \rightarrow Z$ is a weak equivalence in $\fancyscript{M}_\fancyscript{L}$ if for every $\fancyscript{L}$-local object W the induced map

  $$\begin{aligned} \mathrm {Map}_\mathscr {C}(Z, W) \rightarrow \mathrm {Map}_\mathscr {C}(Y, W) \end{aligned}$$

  is a Kan equivalence.

The existence of the $\fancyscript{L}$-localized model structure is proven using the theory of left Bousfield localizations.

For a careful and detailed proof of the existence of left Bousfield localizations see [25, Theorem 4.1.1] For a nice summary of this proof that goes over the main steps see [40, Proposition 9.1].

Using a variation of Bousfield localization and ideas from [35] get right induced model structures.

Theorem 1.8

Let

be an adjunction, such that the following conditions hold:

• 1. $\mathscr {C}$ is a simplicial, locally presentable category.

• 2. $\mathscr {D}^\fancyscript{M}$ is a simplicial, left proper, combinatorial model category

• 3. G preserves filtered colimits

• 4. $\mathscr {C}$ has a functorial fibrant replacement, meaning there is a functor $R: \mathscr {C}\rightarrow \mathscr {C}$ and natural transformation $X \rightarrow RX$, such that $GX \rightarrow GRX$ is a fibrant replacement in $\mathscr {D}$.

Then there exists a unique simplicial, combinatorial, left proper model structure on $\mathscr {C}^\fancyscript{N}$, called the right induced model structure, and characterized by the fact that a map $f: c \rightarrow d$ in $\mathscr {C}^\fancyscript{N}$ is a fibration (weak equivalence) if and only if Gf is a fibration (weak equivalence) in $\mathscr {D}^\fancyscript{M}$.

The proof is a combination of results [19, Theorem 3.6, Theorem 3.8, Corollary 4.14].

There is also another version of a Bousfield localization we need.

Theorem 1.9

[31, A.3.7.10] Let $\mathscr {C}^\fancyscript{M}$ and $\mathscr {D}^\fancyscript{N}$ be left proper combinatorial simplicial model categories such that cofibrations on in $\mathscr {C}^\fancyscript{M}$ and $\mathscr {D}^\fancyscript{N}$ are monomorphisms and suppose we are given a simplicial Quillen adjunction

Then

• 1. There exists a new left proper combinatorial simplicial model structure $\mathscr {C}^{\fancyscript{M}'}$ on the category $\mathscr {C}$ with the following properties:

  • A morphism f in $\mathscr {C}^{\fancyscript{M}'}$ is a cofibration if and only if it is a cofibration in $\mathscr {C}^{\fancyscript{M}}$.

  • A morphism f in $\mathscr {C}^{\fancyscript{M}'}$ is a weak equivalence if and only if Ff is a weak equivalence in $\mathscr {D}^\fancyscript{N}$.

  • A morphism in f in $\mathscr {C}^{\fancyscript{M}'}$ is a fibration if and only if it has the right lifting property with respect to trivial cofibrations.

• 2. The functors F and G determine a new simplicial Quillen adjunction

  

• 3. If the the derived right adjoint is fully faithful then the Quillen adjunction is a Quillen equivalence.

Finally, we want to observe how a Quillen equivalence of model categories can be transferred to over-categories.

Proposition 1.10

Let $\mathscr {C}^\fancyscript{M}$ and $\mathscr {D}^\fancyscript{N}$ be two model categories in which all objects are cofibrant and let

be a Quillen adjunction. Fix an object $C \in \mathscr {C}$. Then the adjunction

is a Quillen adjunction. Here $F(C' \rightarrow C) = FC' \rightarrow FC$ and $u^*G(D \rightarrow FC)= (u_C)^*(GD \rightarrow GFC)$ where $u_C: C \rightarrow GFC$ is the unit map of the adjunction. Moreover, if (F, G) is simplicial (or a Quillen equivalence) then $(F,u^*G)$ is also simplicial (or a Quillen equivalence).

2.4 Model structures for $(\infty ,1)$-categories and their equivalence

There are now many different approaches to the theory of $(\infty ,1)$-categories. Here we focus on two very popular models. Quasi-categories and complete Segal spaces.

Quasi-categories were first introduced by Boardman and Vogt in their study of homotopy coherent algebraic structures [11]. It was Joyal who realized that quasi-categories can be used to do concrete category theory [27, 28] and then later Lurie, who developed all of category theory in the context of quasi-categories [31, 34]. Here we only review the definition and the existence of a model structure.

Definition 1.11

[31, Definition 1.1.2.4] A quasi-category is a simplicial set S that has right lifting property with respect to diagrams

where $0< i < n$.

Quasi-categories have many characteristics of a category. In particular, the set $S_0$ is the set of objects, $S_1$ are the morphisms. Moreover, $S_{hoequiv} \subseteq S_1$ is the subset of $S_1$ consisting of the equivalences in $S_1$. Quasi-categories come with a model structure.

Theorem 1.12

[31, Theorem 2.2.5.1] There is a unique, combinatorial, left proper model structure on $s\mathscr {S}\text {et}$, called the Joyal model structure and denoted $s\mathscr {S}\text {et}^{Joy}$, with the following specifications:

• A map $S \rightarrow T$ is a cofibration if it is a monomorphism.

• An object S is fibrant if it is a quasi-category.

Another popular model of $(\infty ,1)$-categories are complete Segal spaces, which were defined and studied by Charles Rezk [40].

Definition 1.13

Let G(n) be the sub-simplicial space of F(n) consisting of maps $f: [k] \rightarrow [n]$ such that $f(k) - f(0) \le 1$. Define the sets $\fancyscript{S}\mathrm {eg}$ and $\fancyscript{C}\mathrm {omp}$ as follows:

$$\begin{aligned} \fancyscript{S}\mathrm {eg}= & {} \{ G(n) \hookrightarrow F(n) : n \ge 2 \}\\ \fancyscript{C}\mathrm {omp}= & {} \{ F(0) \rightarrow E(1) \} \end{aligned}$$

Notation 1.14

We denote the subobject of $\varDelta [n]$ that is defined similarly to G(n) by $\mathrm {Sp}[n]$.

Definition 1.15

[40, 6] A Reedy fibrant simplicial space W is called a complete Segal space if for every map $f: A \rightarrow B$ in $\fancyscript{S}\mathrm {eg}\cup \fancyscript{C}\mathrm {omp}$, the induced map

$$\begin{aligned} \mathrm {Map}_{s\mathscr {S}}(B,W) \rightarrow \mathrm {Map}_{s\mathscr {S}}(A,W) \end{aligned}$$

is a Kan equivalence.

Similar to quasi-categories, complete Segal spaces have the characteristics of a category. In particular, the elements in $W_{00}$ are the objects and the elements in $W_{10}$. Moreover, the denote the subspace of $W_1$ consisting of equivalence by $W_{hoequiv} \subseteq W_1$ (following [40, Section 6]. The definition already suggests that complete Segal spaces are fibrant objects in a model structure.

Theorem 1.16

[40, Theorem 7.2] There is a unique simplicial combinatorial, left proper model structure on the category of simplicial spaces, called the complete Segal space model structure and denoted by $s\mathscr {S}^{CSS}$, given by the following specifications:

• 1. A map $f: Y \rightarrow Z$ is a cofibration if it is a monomorphism.

• 2. An object W is fibrant if it is a complete Segal space.

• 3. A map $f: Y \rightarrow Z$ is a weak equivalence if for every complete Segal space W the induced map

  $$\begin{aligned} \mathrm {Map}_{s\mathscr {S}}(Z,W) \rightarrow \mathrm {Map}_{s\mathscr {S}}(Y,W) \end{aligned}$$

  is a Kan equivalence.

Before we proceed to the comparison between complete Segal spaces and quasi-categories, we want to generalize complete Segal spaces to complete Segal objects.

Let $\mathscr {C}^\fancyscript{M}$ be a model category. The fact that $\mathscr {C}$ has small coproducts implies that we have a functor

$$\begin{aligned} \fancyscript{C}\mathrm {op}: \mathscr {S}\text {et}\rightarrow \mathscr {C}, \end{aligned}$$

uniquely characterized by the fact that it takes the one element set to the final object in $\mathscr {C}$. This can be extended to a functor of simplicial objects:

$$\begin{aligned} \mathrm {s}\fancyscript{C}\mathrm {op}: s\mathscr {S}\text {et}\rightarrow s\mathscr {C}\end{aligned}$$

Now we can use this notation for following definition.

Definition 1.17

For a given category $\mathscr {C}$ define the sets $\fancyscript{S}\mathrm {eg}_\fancyscript{M}$ and $\fancyscript{C}\mathrm {omp}_\fancyscript{M}$ as

$$\begin{aligned}&\fancyscript{S}\mathrm {eg}_\fancyscript{M}= \{ \mathrm {s}\fancyscript{C}\mathrm {op}(\mathrm {Sp}[n] \hookrightarrow \varDelta [n]) : n \ge 2 \}\\&\fancyscript{C}\mathrm {omp}_\fancyscript{M}= \{ \mathrm {s}\fancyscript{C}\mathrm {op}(\varDelta [0] \hookrightarrow J[1]) \} \end{aligned}$$

Definition 1.18

Let $\mathscr {C}^\fancyscript{M}$ be a combinatorial, simplicial, left proper model category such that the cofibrations are the monomorphisms. A functor $W: \varDelta ^{op} \rightarrow \mathscr {C}$ is called a complete Segal object if it satisfies following conditions:

• 1. It is fibrant in $s\mathscr {C}^{Ree_\fancyscript{M}}$.

• 2. For every morphism $A \rightarrow B$ in $\fancyscript{S}\mathrm {eg}_\fancyscript{M}\cup \fancyscript{C}\mathrm {omp}_\fancyscript{M}$ and every object K in $\mathscr {C}$ the induced map

  $$\begin{aligned} \mathrm {Map}_{s\fancyscript{M}}(B \times K , W) \rightarrow \mathrm {Map}_{s\fancyscript{M}}(A \times K,W) \end{aligned}$$

  is a Kan equivalence.

Theorem 1.19

Let $\mathscr {C}^\fancyscript{M}$ be a combinatorial, simplicial, left proper model category such that the cofibrations are monomorphisms. Then there exists a unique combinatorial, simplicial, left proper model category structure on the category $s\mathscr {C}$, denoted $s\mathscr {C}^{CSO_\fancyscript{M}}$ and called the complete Segal object model structure, such that it satisfies following conditions:

• 1. A map $A \rightarrow B$ is a cofibration if it is a monomorphism of simplicial objects.

• 2. An object W is fibrant if it is a complete Segal object.

• 3. A map of simplicial objects $Y \rightarrow Z$ is a weak equivalence if the induced map

  $$\begin{aligned} \mathrm {Map}_{s\mathscr {C}}(Z,W) \rightarrow \mathrm {Map}_{s\mathscr {C}}(Y,W) \end{aligned}$$

  is a Kan equivalence for every complete Segal object W.

We will often simplify the notation to $s\mathscr {C}^{CSO}$, if the model structure $\fancyscript{M}$ is clear from the context.

Proof

By Theorem 1.2, $s\mathscr {C}^{Ree_\fancyscript{M}}$ is also combinatorial, simplicial and left proper and where the cofibrations are monomorphisms. In particular, $s\mathscr {C}$ is locally presentable and so we can choose a get of generators $\fancyscript{I}$ Hence, by Theorem 1.7, we can construct the localized model structure $s\mathscr {C}^{(Ree_\fancyscript{M})_{\fancyscript{L}}}$, where

$$\begin{aligned} \fancyscript{L}= \{ A \times K \rightarrow B \times K | A \rightarrow B \in \fancyscript{S}\mathrm {eg}_\fancyscript{M}\cup \fancyscript{C}\mathrm {omp}_\fancyscript{M}, K \in \fancyscript{I} \} \end{aligned}$$

which immediately satisfies the desired results.

Remark 1.20

See [42, Proposition 2.2.9] for more details about the complete Segal object model structure (there called Rezk object) and other properties it inherits from $\mathscr {C}^\fancyscript{M}$.

Finally, the complete Segal objects are also homotopy invariant.

Theorem 1.21

Let

be a Quillen equivalence of combinatorial, simplicial, left proper model structures. Then the induced adjunction

is also a Quillen equivalence.

Proof

This follows directly from combining Lemma 1.4 and Theorem 1.9.

Until now we have claimed that quasi-categories and complete Segal spaces are two models of $(\infty ,1)$-categories. This requires knowing that they are in fact equivalent. This was proven by Joyal and Tierney [29], who constructed two Quillen equivalences between complete Segal spaces and quasi-categories that will play an important role later on and hence we will review here.

Let

$$\begin{aligned} p_1: \varDelta \times \varDelta \rightarrow \varDelta \end{aligned}$$

be the projection functor that takes ([n], [m]) to [n].

Similarly, let

$$\begin{aligned} i_1: \varDelta \rightarrow \varDelta \times \varDelta \end{aligned}$$

be the inclusion functor that takes [n] to ([n], [0]).

Theorem 1.22

[29, Theorem 4.11] The induced adjunction

is a Quillen equivalence between the Joyal model structure and the complete Segal space model structure. Here $i_1^*$ and $p_1^*$ are defined by precomposition via the functors $i_1$ and $p_1$.

We move on to the second Quillen equivalence. Let

$$\begin{aligned} t: \varDelta \times \varDelta \rightarrow s\mathscr {S}\text {et}\end{aligned}$$

be the functor defined as $t([n],[m]) = \varDelta [n] \times J[m]$.

Theorem 1.23

[29, Theorem 4.12] Let

be the adjunction induced by the map t (meaning $t_!$ is the left Kan extension). Then this adjunction is a Quillen equivalence between the complete Segal space model structure and the Joyal model structure. Here $t_!$ is the left Kan extension along t and $t^!$ is the right adjoint of the left Kan extension.

Remark 1.24

The adjunction $(t_!,t^!)$ is not simplicial adjunction (in fact the Joyal model structure is not even simplicial). However, the adjunction is enriched over the Joyal model structure. So, in particular, for two quasi-categories S, T we have an equivalence of complete Segal spaces

$$\begin{aligned} t^!(T^S) \rightarrow t^!T^{t^!S} \end{aligned}$$

For a detailed discussion of this enrichment see [42, Example 2.2.6]

The goal is to show that with some minor adjustments we can generalize these two Quillen equivalences to Quillen equivalences between various notions of Cartesian fibrations.

2.5 Contravariant model structures

In this subsection we define the contravariant model structure for simplicial spaces and simplicial sets and observe that they are in fact Quillen equivalent.

Let us start with the case of simplicial spaces.

Definition 1.25

[37, Definition 3.2, Remark 4.24] Let X be a simplicial space. A map $p: R \rightarrow X$ is called right fibration if it is a Reedy fibration and the following is a homotopy pullback square:

where $< n>:F(0) \rightarrow F(n)$ is the map that takes the point to $n \in F(n)_0$.

Right fibrations come with a model structure.

Theorem 1.26

[37, Theorem 3.12, Remark 4.24] Let X be simplicial space. There is a unique simplicial, combinatorial, left proper model structure on the category $s\mathscr {S}_{/X}$, called the contravariant model structure and denoted by $(s\mathscr {S}_{/X})^{contra}$, which satisfies the following conditions:

• 1. An object $R \rightarrow X$ is fibrant if it is a right fibration.

• 2. A map $Y \rightarrow Z$ over X is a cofibration if it is a monomorphism.

• 3. A map $f: Y \rightarrow Z$ over X is a weak equivalence if

  $$\begin{aligned} \mathrm {Map}_{/X}(Z,R) \rightarrow \mathrm {Map}_{/X}(Y,R) \end{aligned}$$

  is an equivalence for every right fibration $R \rightarrow X$.

Now we can move on to the case of simplicial sets.

Definition 1.27

[31, Definition 2.0.0.3] A map of simplicial sets $p: R \rightarrow S$ is a right fibration if it has the right lifting property with respect to squares

where $n \ge 0$ and $0 < i \le n$.

Similar to above, we can define a model structure with fibrant objects right fibrations.

Theorem 1.28

[31, Proposition 2.1.4.7, Proposition 2.1.4.8, Proposition 2.1.4.9, Remark 2.1.4.12] Let S be a simplicial set. There is a unique simplicial, combinatorial, left proper model structure on the category of simplicial sets over S, called the contravariant model structure and denoted by $(s\mathscr {S}\text {et}_{/S})^{contra}$, such that

• 1. An object $R \rightarrow S$ is fibrant if it is a right fibration.

• 2. A map $T \rightarrow U$ over S is a cofibration if it is a monomorphism.

• 3. A map $T \rightarrow U$ over S is a weak equivalence if the induced map

  $$\begin{aligned} \mathrm {Map}_{/S}(U,R) \rightarrow \mathrm {Map}_{/S}(T,R) \end{aligned}$$

  is a Kan equivalence for every right fibration $R \rightarrow S$.

Notice, we called both model structures (Theorems 1.28, 1.26) contravariant, as they are in fact Quillen equivalent.

Theorem 1.29

[37, Theorem B.12, Theorem B.13] Let S be a simplicial set and X a simplicial space. There are Quillen equivalences of contravariant model structures

2.6 Cartesian fibrations of bisimplicial objects

In this subsection we review the complete Segal approach towards Cartesian fibrations and then prove the analogous results for Cartesian fibrations of bisimplicial sets. The case for bisimplicial spaces has been studied in great detail in [38].

Let X be a simplicial space. We denote by X the bisimplicial space defined as $X_{kn} = X_n$.

Definition 1.30

[38, Section 4] Let X be a simplicial space. A map of bisimplicial spaces $Y_{\bullet \bullet } \rightarrow X$ is a Cartesian fibration if it satisfies following three conditions:

• 1. $Y \rightarrow X$ is a Reedy fibration in $ss\mathscr {S}$.

• 2. For each k, the map of simplicial spaces $Y_{k\bullet } \rightarrow X_\bullet$ is a right fibration.

• 3. The map of simplicial spaces $Y_{\bullet n} \rightarrow X_n$ is a complete Segal space fibration.

Remark 1.31

As X is a simplicial space, we have an isomorphism of categories

$$\begin{aligned} ss\mathscr {S}_{/X} \cong \mathrm {Fun}(\varDelta ^{op}, s\mathscr {S}_{/X}) \end{aligned}$$

Using this isomorphism we can fact replace condition (2) and (3) with condition

• (3’) The corresponding simplicial functor

  $$\begin{aligned} Y: \varDelta ^{op} \rightarrow s\mathscr {S}_{/X} \end{aligned}$$

  is a complete Segal object in the contravariant model structure on $s\mathscr {S}_{/X}$.

Indeed, the fact that $Y_k$ is fibrant in the contravariant model structure precisely means that $Y_k$ is a right fibration, which is condition (2). Moreover, $Y \rightarrow X$ being a complete Segal object is precisely the statement that $Y_{\bullet n} \rightarrow X_n$ is a complete Segal space fibration giving us (3).

Theorem 1.32

[38, Section 4] Let X be a simplicial space. There is a unique simplicial combinatorial left proper model structure on $ss\mathscr {S}_{/X}$, called the Cartesian model structure and denoted $(ss\mathscr {S}_{/X})^{Cart}$, such that

• An object $C \rightarrow X$ is fibrant if it is a Cartesian fibration (Definition 1.30).

• A map $Y \rightarrow Z$ over X is a cofibration if it is a monomorphism.

• A map $Y \rightarrow Z$ over X is a weak equivalence if for every Cartesian fibration $C \rightarrow X$, the induced map

  $$\begin{aligned} \mathrm {Map}_{/X}(Z,C) \rightarrow \mathrm {Map}_{/X}(Y,C) \end{aligned}$$

  is a Kan equivalence.

Remark 1.33

It follows from Remark 1.31 that this model structure is in fact the complete Segal object model structure on the contravariant model structure on simplicial spaces over X, as constructed in Theorem 1.19.

For more details about the Cartesian model structure (in particular various ways of characterizing its fibrant objects and weak equivalences) see [38].

We now move on to the analogous result for Cartesian fibrations of bisimplicial sets. For a given simplicial set S, we denote by S the bisimplicial set defined as $S_{kn} = S_n$.

Definition 1.34

An object $T \rightarrow S$ in $ss\mathscr {S}\text {et}_{/S}$ is a Cartesian fibration if the corresponding functor

$$\begin{aligned} T: \varDelta ^{op} \rightarrow (s\mathscr {S}\text {et}_{/S})^{contra} \end{aligned}$$

is a complete Segal object (Definition1.18) in the contravariant model structure on $(s\mathscr {S}\text {et}_{/S})^{contra}$.

We want an analogous result about Cartesian fibrations of bisimplicial sets. Here we can simply combine Theorems 1.21, 1.26, and 1.19 to get following extensive result.

Theorem 1.35

Let S be a simplicial sets. There exists a unique, simplicial, combinatorial, left proper model structure on the category of bisimplicial sets over S, $ss\mathscr {S}\text {et}_{/S}$, called the Cartesian model structure and denoted $(ss\mathscr {S}\text {et}_{/S})^{Cart}$ with following properties:

• 1. An object $C \rightarrow S$ is fibrant if it is a Cartesian fibration (Definition 1.34).

• 2. A map of bisimplicial sets $T \rightarrow U$ over S is a cofibration if it is a monomorphism.

• 3. A map $T \rightarrow U$ over S is a weak equivalence if for every Cartesian fibration $C \rightarrow S$, the induced map

  $$\begin{aligned} \mathrm {Map}_{/S}(U,C) \rightarrow \mathrm {Map}_{/S}(T,C) \end{aligned}$$

  is a Kan equivalence.

Moreover, we have Quillen equivalences:

3 Marked simplicial spaces and Cartesian fibrations

In Sect. 1.6 we defined two Cartesian model structures: for bisimplicial spaces and for bisimplicial sets. As mentioned before, the Cartesian model structure for marked simplicial sets had already been defined [31]. This leaves us with one last Cartesian model structure: marked simplicial spaces, which is the goal of this section.

3.1 Marked simplicial spaces

In this subsection we want to study marked simplicial spaces. We first review marked simplicial sets as studied in [31].

Definition 2.1

A marked simplicial set is a pair (S, A) where S is a simplicial set and $A \subset S_1$ such that A includes all degenerate edges. A morphism of marked simplicial sets $f:(S,A) \rightarrow (T,B)$ is a map of simplicial sets $f: S \rightarrow T$ such that $f(A) \subset B$. We denote the category of marked simplicial sets by $s\mathscr {S}\text {et}^+$.

We want to study the category of marked simplicial sets $s\mathscr {S}\text {et}_+$. As we have the additional data of markings, the objects are not just simplicial objects. We thus need an alternative approach.

Definition 2.2

Let $\varDelta ^+$, the marked simplex category, be the category defined as the pushout

where the top and left hand maps are the evident inclusion maps (note there is a unique map $[1] \rightarrow [0]$ in $\varDelta$).

Using our intuition about $\varDelta$, we can depict this category as follows:

where the evident triangle is commutative.

We would like to prove that a marked simplicial set is just a presheaf on $\varDelta ^+$, where the image of $[1^+]$ is the set of markings. However, for that we need the additional assumption that the image of the map $[1^+] \rightarrow [1]$ is an injection of sets. Hence, marked simplicial sets are certain separated presheaves on $\varDelta ^+$.

Lemma 2.3

Let $\mathscr {J}$ be the Grothendieck topology on $\varDelta ^+$ where the only non-trivial cover is $[1] \rightarrow [1^+]$. Then the category of marked simplicial sets is isomorphic to the category of separated set valued presheaves on $\varDelta ^+$ with the topology $\mathscr {J}$.

Proof

By definition $F: \varDelta ^+ \rightarrow \mathscr {S}\text {et}$ is separated if it takes covering maps to monomorphisms. Hence, F is separated with respect to the topology $\mathscr {J}$ if and only if $F([1^+]) \rightarrow F([1])$ is a monomorphism which means it is a marked simplicial set, where the markings are $F([1^+])$.

It is now immediate to confirm that a natural transformation of functors corresponds to maps of marked simplicial sets.

Remark 2.4

This lemma is also proven (independently) in [3].

Remark 2.5

This lemma proves that the category of marked simplicial sets is equivalent to a category of separated presheaves, meaning it is a quasi-Grothendieck topos [26, C2.2.13], which has far-reaching implications:

• 1. $s\mathscr {S}\text {et}^+$ has small limits and colimits

• 2. $s\mathscr {S}\text {et}^+$ is a presentable category.

• 3. $s\mathscr {S}\text {et}^+$ is locally Cartesian closed, which for two objects (X, A), (Y, B) we denote by $(Y,B)^{(X,A)}$.

Notation 2.6

We will make ample use of the fact that marked simplicial objects are subcategories of presheaf categories. Hence we generalize our notational conventions from Sect. 1.1 and denote the generators of $\mathrm {Fun}((\varDelta ^+)^{op},\mathscr {S}\text {et})$ by $\varDelta ^+[n]$. Notice, here n is an object in $\varDelta ^+$ and so we can also have $n = 1^+$.

Finally, we need to realize how marked simplicial sets are related to simplicial sets [31, Definition 3.1.0.1].

Remark 2.7

There is a functor $\mathrm {inc}:\varDelta \rightarrow \varDelta ^+$, which is the identity on objects and gives us a chain of adjunctions

which restricts to adjunctions

Here $\mathrm {Unm}$ simply forgets the markings and, for a given simplicial set S, we have $S^\flat = (S,S_0)$ and $S^\# = (S,S_1)$.

Remark 2.8

We can use the standard simplices $\varDelta [n]$ and the functors $(-)^\flat$ and $(-)^\sharp$ to get following valuable isomorphisms:

$$\begin{aligned}&\mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\varDelta [n]^{\flat }, (S,A)) \cong S_n,\\&\mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\varDelta [1]^\sharp , (S,A)) \cong A, \end{aligned}$$

for all marked simplicial sets (S, A) and $n \ge 0$.

Having done a careful analysis of marked simplicial sets, we are finally ready to study marked simplicial spaces.

Definition 2.9

A marked simplicial space is a pair (X, A), where X is a simplicial space and $A \hookrightarrow X_1$ is an inclusion of spaces such that the degeneracy map $s_0: X_0 \rightarrow X_1$ takes value in A. We say X is the underlying simplicial space and A is the space of markings.

Definition 2.10

A map of marked simplicial spaces $f:(X,A) \rightarrow (Y,B)$ is a map of simplicial spaces $f: X \rightarrow Y$ such that $f_1$ restricts to a map $(f_1)|_A: A \rightarrow B$. Marked simplicial spaces with the morphisms described before form a category which we denote by $s\mathscr {S}^+$.

We now want to proceed to study the category of marked simplicial spaces. Comparing Definitions 2.1 and 2.9 it immediately follows that a marked simplicial space is just a simplicial object in the category of marked simplicial sets. Hence, we get the following lemma that allows us to straightforwardly generalize results from marked simplicial sets to marked simplicial spaces.

Lemma 2.11

There is an equivalence of categories $\mathrm {Fun}(\varDelta , s\mathscr {S}\text {et}^+) \cong s\mathscr {S}^+$.

Remark 2.12

The equivalence immediately has following implications:

• 1. $s\mathscr {S}^+$ has small limits and colimits and presentable.

• 2. $s\mathscr {S}^+$ is locally Cartesian closed, which for two objects (X, A), (Y, B) we denote by $(Y,B)^{(X,A)}$.

• 3. Similarly, we denote the generators of $\mathrm {Fun}(\varDelta ^+,\mathscr {S})$ by $F^+(n) \times \varDelta [l]$. Notice, here n is again an object in $\varDelta ^+$, whereas l is an object in $\varDelta$.

• 4. There are adjunctions

  

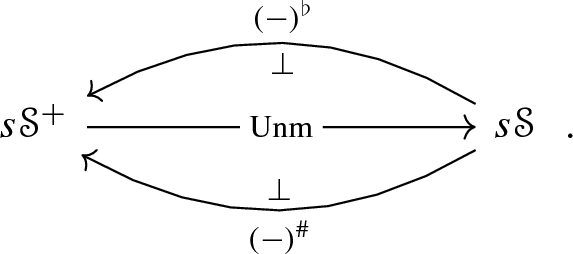
  Here $\mathrm {Unm}$ simply forgets the markings and, for a given simplicial space X, we have $X^\flat = (X,X_0)$ and $X^\# = (X,X_1)$.

• 5. Using $\mathrm {Unm}$ we can define a simplicial enrichment

  $$\begin{aligned} \mathrm {Map}_{s\mathscr {S}^+}((X,A),(Y,B)) = \mathrm {Unm}((Y,B)^{(X,A)})_0. \end{aligned}$$

• 6. Finally, we have

  $$\begin{aligned}&\mathrm {Map}_{s\mathscr {S}^+}(F(n)^{\flat }, (X,A)) \cong X_n,\\&\mathrm {Map}_{s\mathscr {S}^+}(F(1)^\sharp , (X,A)) \cong A, \end{aligned}$$

  for all marked simplicial spaces (X, A) and $n \ge 0$.

3.2 Marked Joyal model structure vs. marked CSS model structure

In this subsection we want to generalize the Joyal and complete Segal space model structures to marked simplicial sets and spaces. The first step is to adjust the Joyal-Tierney adjunctions (Theorem 1.22,Theorem 1.23) to marked objects.

Let

$$\begin{aligned} i_1^+: \varDelta ^+ \rightarrow \varDelta ^+ \times \varDelta \end{aligned}$$

be the map that takes an object [n] to ([n], [0]). Similarly, let

$$\begin{aligned} p_1^+: \varDelta ^+ \times \varDelta \rightarrow \varDelta ^+ \end{aligned}$$

be the functor that takes a pair ([n], [m]) to [n].

Definition 2.13

Let

be the adjunction induced by the maps $i_1^+, p_1^+$.

We claim this adjunction restricts to marked objects.

Lemma 2.14

The functors $(p_1^+)^*,(i_1^+)^*$ take marked objects to marked object. Hence, they restrict to an adjunction

Proof

Let $G: (\varDelta ^+)^{op} \rightarrow \mathscr {S}\text {et}$ be a presheaf that corresponds to a marked simplicial set, meaning the map $G(1^+) \rightarrow G(1)$ is a monomorphism. We need to show that $(p_1^+)^*(G)(1^+,l) \rightarrow (p_1^+)^*(G)(1,l)$ is a monomorphism as well. However, by direct computation $(p_1^+)^*(G)(1^+,l) \rightarrow (p_1^+)^*(G)(1,l) = G(1^+) \rightarrow G(1)$ and so the result follows from our assumption.

On the other hand, assume $G: (\varDelta ^+)^{op} \times \varDelta ^{op} \rightarrow \mathscr {S}\text {et}$ be a presheaf that corresponds to marked simplicial space. We want to prove $(i_1^+)^*(G): (\varDelta ^+)^{op} \rightarrow \mathscr {S}\text {et}$ corresponds to a marked simplicial set, meaning we have to show $(i_1^+)^*(G)(1^+) \rightarrow (i_1^+)^*(G)(1)$ is a monomorphism. By direct computation, this map is given by $G(1^+,0) \rightarrow G(1,0)$, which is a monomorphism by assumption.

We now move on to adjust the second adjunction, $(t_!,t^!)$, to the marked setting.

Let

$$\begin{aligned} \tau : \varDelta ^+ \rightarrow s\mathscr {S}\text {et}^+ \end{aligned}$$

be the marked simplicial diagram defined as

$$\begin{aligned} \tau ([n]) = {\left\{ \begin{array}{ll} \varDelta [n]^{\flat } &{} \text { if } n \ne 1^+ \\ \varDelta [1]^\sharp &{} \text { if } n = 1^+ \end{array}\right. }, \end{aligned}$$

where the cosimplicial maps between $\varDelta [n]^\flat$ are given by the cosimplicial diagram $\varDelta$ in $s\mathscr {S}\text {et}$ and the map $\varDelta [1]^\flat \rightarrow \varDelta [1]^\sharp$ is the evident inclusion map.

We can depict the marked cosimplicial object $\tau$ in $s\mathscr {S}\text {et}^+$ as

Using $\tau$ we can now define a functor

$$\begin{aligned} t^+: \varDelta ^+ \times \varDelta \rightarrow s\mathscr {S}\text {et}^+ \end{aligned}$$

by $t^+([n],[m]) = \tau (n) \times \varDelta [n]^\#$. We can extend this functor to an adjunction.

Definition 2.15

Let

be the adjunction given by left Kan extension along $t^+$.

The right hand side of the adjunction already takes value in marked simplicial sets, so we only need to prove that the right adjoint takes value in marked simplicial spaces as well.

Lemma 2.16

The adjunction $((t^+)_!,(t^+)^!)$ restricts to an adjunction

Proof

Let (X, A) be a marked simplicial set. Then

$$\begin{aligned} (t^+)^!(X,A)_{nl}= \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\tau (n) \times \varDelta [l]^\#, (X,A)) \cong \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\tau (n), (X,A)^{\varDelta [l]^\#}), \end{aligned}$$

where the isomorphism follows from the fact that $s\mathscr {S}\text {et}^+$ is Cartesian closed (Remark 2.5).

In order to show that $(t^+)^!(X,A)$ is a marked simplicial space we have to prove that map

$$\begin{aligned} \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\tau (1^+) \times \varDelta [l]^\#, (X,A)) \rightarrow \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\tau (1) \times \varDelta [l]^\#, (X,A)) \end{aligned}$$

is an injection for all $l \ge 0$. By direct computation this map is given by

$$\begin{aligned} \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\varDelta [1]^\sharp \times \varDelta [l]^\#, (X,A)) \rightarrow \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\varDelta [1]^\flat \times \varDelta [l]^\#, (X,A)). \end{aligned}$$

By the isomorphism above, this is isomorphic to

$$\begin{aligned} \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\varDelta [1]^\sharp , (X,A)^{\varDelta [l]^\#}) \rightarrow \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\varDelta [1]^\flat , (X,A)^{\varDelta [l]^\#}). \end{aligned}$$

Finally, by Remark 2.8, the right hand side is the set of 1-simplices in $(X,A)^{\varDelta [l]^\#}$, whereas the left hand side are the marked ones. Hence, this map is an injection by assumption.

Remark 2.17

Recall that $t: \varDelta \times \varDelta \rightarrow s\mathscr {S}\text {et}$ was defined as $t([n],[m]) = \varDelta [n] \times J[m]$ (Theorem 1.22). Hence our first guess for a generalization to marked simplicial spaces might have been $t'([n],[m]) = \tau ([n]) \times J[m]^\flat$.

This functor would in fact give us an adjunction between marked simplicial spaces and marked simplicial sets and we could use that to construct Quillen equivalences. However, in Theorem 2.22 we will observe that the model structure of interest on $s\mathscr {S}\text {et}^+$, the marked Joyal structure, is in fact a simplicial model structure, and that the simplicial enrichment makes $((t^+)_!, (t^+)^!)$ into a simplicial Quillen equivalence (Theorem 2.25). If we used $((t')_!,(t')^!)$ instead we would not get a simplicial Quillen equivalence.

On the other hand, we do in fact use the fact that $((t^+)_!, (t^+)^!)$ is simplicial, particularly in Theorem 2.25 and Theorem 2.38, to construct our desired model structures on marked simplicial spaces (we need it to apply Theorem 1.9). Hence we have chosen $t^+$ as our generalization t.

More generally, we note that even without any particular application in mind, having a simplicial adjunction of simplicial model structures implies that we immediately get an adjunction of $\infty$-categories between the underlying $\infty$-categories of the simplicial model structures, as proven in [31, Proposition 5.2.4.6], giving additional justification for our choice of generalization.

Remark 2.18

Notice the adjunctions $((t^+)_!,(t^+)^!)$ and $(t_!,t^!)$ do not give us a commutative square. Thus our choice of prioritizing a simplicial Quillen equivalence (as explained in Remark 2.17) comes at the price of not commuting with the original adjunction $(t_!,t^!)$.

We now want to move on and prove that the adjunctions $((p_1^+)^*,(i_1^+)^*)$ and $((t^+)_!,(t^+)^!)$ do in fact give us a Quillen equivalence, similar to the unmarked counter-parts.

For that we first have to construct appropriate model structures, which we will do in two steps:

• 1. First we define a model structure $s\mathscr {S}^+$ which is transferred from a model structure on $s\mathscr {S}$ and does not take the markings into account (Proposition 2.19).

• 2. Then we localize this model structure such that the fibrancy condition depends on an appropriate choice of marking (Theorem 2.25).

Proposition 2.19

Let $\fancyscript{L}$ be a set of cofibrations of simplicial spaces. There is a unique combinatorial simplicial left proper model structure on the category of marked simplicial spaces, called the unmarked $\fancyscript{L}$-localized model structure and denoted by $(s\mathscr {S}^+)^{un^+Ree_{\fancyscript{L}}}$, with the following specifications:

• F A map $(X,A) \rightarrow (Y,B)$ is a fibration if the underlying map of simplicial spaces $X \rightarrow Y$ is a fibration in the $\fancyscript{L}$ localized Reedy model structure.

• W A map $(X,A) \rightarrow (Y,B)$ is a weak equivalence if the underlying map of simplicial spaces $X \rightarrow Y$ is a weak equivalence in the $\fancyscript{L}$-localized Reedy model structure.

• C A map of marked simplicial spaces is a cofibration if it has the left lifting property with respect to maps that are simultaneously fibrations and weak equivalences.

Moreover, the adjunction

is a Quillen equivalence. Here the left hand side has the $\fancyscript{L}$-localized model structure (Theorem 1.7) and the right side the unmarked $\fancyscript{L}$-localized model structure.

Proof

In order to construct a model structure on $s\mathscr {S}^+$ we want to prove that we can use the adjunction

(2.1)

to induce the $\fancyscript{L}$-localized Reedy model structure via the right adjoint $\mathrm {Unm}$. This would immediately give us most of the desired results, up to including that the adjunction is a Quillen adjunction, leaving us only with the task of showing it is a Quillen equivalence.

We will hence check the required conditions of right-induced model structures (Theorem 1.8):

• $\mathrm {Unm}$ commutes with filtered colimits: This follows from the fact that $\mathrm {Unm}$ is a left adjoint (Remark 2.12).

• $s\mathscr {S}^+$ is simplicial: Also proven in Remark 2.12.

• There is a functorial fibrant replacement functor in $s\mathscr {S}^+$: Let R be a fibrant replacement functor in $s\mathscr {S}^{Ree_{\fancyscript{L}}}$. Then the functor

  $$\begin{aligned} s\mathscr {S}^+ \xrightarrow { \ \mathrm {Unm}\ } s\mathscr {S}\xrightarrow { \ R \ } s\mathscr {S}\xrightarrow { \ (-)^\sharp \ } s\mathscr {S}\end{aligned}$$

  is in fact a fibrant replacement functor in the sense of Theorem 1.8. Indeed, for a given marked simplicial space (X, A) the map $\mathrm {Unm}(X,A) \rightarrow \mathrm {Unm}(R \mathrm {Unm}(X,A)^\sharp )$ is precisely $X \rightarrow RX$, which by definition is the fibrant replacement in the $\fancyscript{L}$-localized Reedy model structure.

We are now left with proving that the Quillen adjunction (2.1) is in fact a Quillen equivalence. The right adjoint reflects weak equivalences by definition and so it suffices to prove the derived unit map is an equivalence for every fibrant simplicial space, however, that is just the identity. Hence we are done.

We can now use this result for particular interesting instances.

Corollary 2.20

If $\fancyscript{L}$ is empty, then we get the unmarked Reedy model structure, $(s\mathscr {S}^+)^{un^+Ree}$, on marked simplicial spaces.

Corollary 2.21

If we take $\fancyscript{L} = \fancyscript{S}\mathrm {eg}\cup \fancyscript{C}\mathrm {omp}$ (the Segal maps and completeness maps as defined in Definition 1.13), then we get the unmarked complete Segal space model structure, denoted $(s\mathscr {S}^+)^{un^+CSS}$.

The reason the model structure is called “unmarked" is that the fibrancy condition is independent of the markings. This has very problematic implications, such as the fact that even some common marked simplicial spaces are not cofibrant anymore. For example the diagram

has no lift, although right hand map is a trivial fibration in the $\fancyscript{L}$-localized marked Reedy model structure. Hence $F(1)^{\sharp }$ is not cofibrant.

We thus want modify the model structure, by restricting the fibrations and trivial fibrations and making it dependent on the markings. In order to do that we want to compare the unmarked CSS model structure with the marked Joyal model structure.

Theorem 2.22

[31, Proposition 3.1.3.7, Proposition 3.1.4.1, Corollary 3.1.4.4, Proposition 3.1.5.3] There is a unique combinatorial, simplicial, left proper model structure on $s\mathscr {S}\text {et}^+$, called the marked Joyal model structure and denoted $s\mathscr {S}\text {et}^{Joy^+}$, with the following specifications:

• 1. A map of marked simplicial sets $f: (S,A) \rightarrow (T,B)$ is a cofibration if the underlying map of simplicial sets $S \rightarrow T$ is a monomorphism.

• 2. A map of marked simplicial sets $f: (S,A) \rightarrow (T,B)$ is a weak equivalence if the underlying map of simplicial sets $S \rightarrow T$ is an equivalence in the Joyal model structure.

• 3. A marked simplicial set (X, A) is fibrant if X is a quasi-category and A is the set of equivalences in X.

• 4. The simplicial enrichment is given by the simplicial set

  $$\begin{aligned} \mathrm {Map}_{s\mathscr {S}\text {et}^+}(S,T) = \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(S \times \varDelta [n]^\sharp , T) \end{aligned}$$

Finally, the adjunction

is a Quillen equivalence between the Joyal model structure and the marked Joyal model structure.

Remark 2.23

This model structure is originally defined in [31] as a special case of the Cartesian model structure for marked simplicial sets (which we will review in Theorem 2.31) and hence does not have its own separate name there.

We want to use the marked Joyal model structure to adjust the unmarked CSS model structure.

Lemma 2.24

The adjunction

is a simplicial Quillen adjunction between the unmarked CSS model structure and the marked Joyal model structure.

Proof

First, the adjunction is in fact simplicial. Indeed, by definition we have $(t^+)_!(\varDelta [n]^\flat ) = \varDelta [n]^\#$, which gives us following natural bijection

$$\begin{aligned}&\mathrm {Map}_{s\mathscr {S}\text {et}^+}((t^+)_!X,S)_n = \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(((t^+)_!X) \times \varDelta [n]^\#,S)\\&\quad = \mathrm {Hom}_{s\mathscr {S}\text {et}^+}((t^+)_!(X \times \varDelta [n]^\flat ),S) \cong \\&\mathrm {Hom}_{s\mathscr {S}^+}(X \times \varDelta [n]^\flat ,(t^+)^!S) = \mathrm {Map}_{s\mathscr {S}^+}(X,(t^+)^!S)_n \end{aligned}$$

As all monomorphisms in $(s\mathscr {S}\text {et}^+)^{Joy^+}$ are cofibrations, the left adjoint $(t^+)_!$ indeed preserves cofibrations. Hence, in order to prove we have a Quillen adjunction it suffices to prove $(t^+)^!$ preserves fibrant objects [31, Corollary A.3.7.2]. However, this is immediate as fibrant objects in marked Joyal model structure are of the form $(S,S_{hoequiv})$ where S is a quasi-category and $\mathrm {Unm}(t^+)^!(S,S_{hoequiv})=t^!(S)$, which is a complete Segal space, by Theorem 1.22, and so $(t^+)^!(S,S_{hoequiv})$ is fibrant in the unmarked complete Segal space model structure.

Using this Quillen adjunction we can finally construct a new model structure on $s\mathscr {S}^+$, in which the fibrant objects depends on the markings!

Theorem 2.25

There exists a unique simplicial, cofibrantly generated, left proper model structure on marked simplicial spaces, denoted $(s\mathscr {S}^+)^{CSS^+}$ and called the marked CSS model structure, characterized by

• 1. Fibrant objects are marked simplicial spaces of the form $(W,W_{hoequiv})$, where W is a complete Segal space and $W_{hoequiv}$ is the subspace of weak equivalences.

• 2. A map $f: (X,A) \rightarrow (Y,B)$ is a cofibration if the map of underlying simplicial spaces $X \rightarrow Y$ is a monomorphism.

• 3. A map $f: (X,A) \rightarrow (Y,B)$ is a weak equivalence if for every fibrant object $(W,W_{hoequiv})$ the induced map

  $$\begin{aligned} \mathrm {Map}_{s\mathscr {S}^+}((Y,B),(W,W_{hoequiv})) \rightarrow \mathrm {Map}_{s\mathscr {S}^+}((X,A),(W,W_{hoequiv})) \end{aligned}$$

  is a Kan equivalence.

• 4. A map between fibrant objects $(W,W_{hoequiv}) \rightarrow (V,V_{hoequiv})$ is a weak equivalence (fibration) if and only if it is a weak equivalence (fibration) in the unmarked CSS model structure.

• 5. The adjunction

  

  (2.2)

  is a simplicial Quillen equivalence of simplicial model structures.

Proof

By Lemma 2.24, we have a simplicial Quillen adjunction

Hence, by applying Theorem 1.9, we get a new model structure on $s\mathscr {S}^+$, which we call the marked CSS model structure. We want to prove that this model structure satisfies all the conditions stated above. We will start by proving that the adjunction $((t^+)_!,(t^+)^!)$ is a Quillen equivalence.

By Theorem 1.9, it suffices to show that the derived right Quillen functor, $(t^+)^!$, is fully faithful. Fix two fibrant objects $(S,S_{hoequiv})$, $(T,T_{hoequiv})$ in $(s\mathscr {S}\text {et}^+)^{Joy^+}$. We want to prove

$$\begin{aligned} \mathrm {Map}_{s\mathscr {S}\text {et}^+}((S,S_{hoequiv}),(T,T_{hoequiv})) \rightarrow \mathrm {Map}_{s\mathscr {S}^+}((t^+)^!(S,S_{hoequiv}),(t^+)^!(T,T_{hoequiv})) \end{aligned}$$

is a Kan equivalence. This will require several computations.

First, we observe that a $\varDelta [n]^\sharp \rightarrow (S,S_{hoequiv})$ sends all edges to weak equivalences, and so we have bijection

$$\begin{aligned} \mathrm {Hom}_{s\mathscr {S}\text {et}^+}((S,S_{hoequiv}), (T, T_{hoequiv})) \cong \mathrm {Hom}_{s\mathscr {S}\text {et}}(S,T). \end{aligned}$$

(2.3)

Moreover, we observe that any map of simplicial sets $S \rightarrow T$ will automatically send $S_{hoequiv}$ to $T_{hoequiv}$. Giving us a Kan equivalence

$$\begin{aligned} \mathrm {Hom}_{s\mathscr {S}\text {et}^+}(\varDelta [n]^\sharp , (S,S_{hoequiv})) \simeq \mathrm {Hom}_{s\mathscr {S}\text {et}}(J[n],S). \end{aligned}$$

(2.4)

Combining these we have

$$\begin{aligned}&\mathrm {Map}_{s\mathscr {S}\text {et}^+}((S,S_{hoequiv}),(T,T_{hoequiv}))_n \\&\quad = \mathrm {Hom}_{s\mathscr {S}\text {et}^+}((S,S_{hoequiv}) \times \varDelta [n]^\sharp , (T, T_{hoequiv})) \overset{(2.28)}{\cong } \\&\mathrm {Hom}_{s\mathscr {S}\text {et}^+}((S,S_{hoequiv}) \times (J[n],J[n]_{hoequiv}), (T,T_{hoequiv})) \overset{(2.29)}{\simeq } \\&\mathrm {Hom}_{s\mathscr {S}\text {et}}(S \times J[n],T) = t^!(T^S)_{0n}. \end{aligned}$$

Next, by the argument in the proof of Lemma 2.24 we have

$$\begin{aligned} (t^+)^!(S,S_hoequiv) = (t^!S,t^!S_{hoequiv}). \end{aligned}$$

(2.5)

Moreover, using the same argument as above, we have a bijection

$$\begin{aligned} \mathrm {Hom}_{s\mathscr {S}^+}((S,S_{hoequiv}), (T, T_{hoequiv})) \cong \mathrm {Hom}_{s\mathscr {S}}(S,T). \end{aligned}$$

(2.6)

Combining these we have

$$\begin{aligned}&\mathrm {Map}_{s\mathscr {S}^+}((t^+)^!(S,S_{hoequiv}),(t^+)^!(T,T_{hoequiv}))_n\\&\quad = \mathrm {Hom}_{s\mathscr {S}^+}((t^+)^!(S,S_{hoequiv}) \times \varDelta [n],(t^+)^!(T,T_{hoequiv})) \overset{(2.30)}{\cong } \\&\mathrm {Hom}_{s\mathscr {S}^+}((t^!S,t^!S_{hoequiv}) \times \varDelta [n],(t^!T,t^!T_{hoequiv})) \overset{(2.31)}{\cong } \\&\mathrm {Hom}_{s\mathscr {S}}(t^!S \times \varDelta [n],t^!T) = ((t^!T)^{t^!S})_{0n}. \end{aligned}$$

Thus, in order to prove that the derived functor $(t^+)^!$ is fully faithful it suffices to prove that the map

$$\begin{aligned} t^!(T^S)_0 \rightarrow (t^!T^{t^!S})_0 \end{aligned}$$

is a Kan equivalence. However, this immediately follows from that fact that the map $t^!(T^S) \rightarrow t^!(T)^{t^!(S)}$ is a CSS equivalence (Remark 1.24). This proves that $((t^+)_!,(t^+)^!)$ is a Quillen equivalence.

We move on to confirm all the properties of the model structure given in the statement of Theorem 2.25.

• 1. We start by characterizing the fibrant objects. By definition of the localization model structure, an object (W, A) is fibrant if it is fibrant in the unmarked CSS model structure, meaning W is a complete Segal space, and it lies in the essential image of the right adjoint $(t^+)^!$, hence $A = W_{hoequiv}$.

• 2. We now move on to prove that cofibrations are monomorphisms. By Theorem 1.9, a map is a cofibration if and only its image under $(t^+)_!$ is a cofibration. However, the cofibrations in the marked Joyal model structure are just the monomorphisms and so the result follows.

• 3. Next we characterize the weak equivalences in the model structure. Notice the marked CSS model structure is simplicial and fibrant objects are of the form $(W,W_{hoequiv})$ and so a map $(Y,A) \rightarrow (Z,B)$ is an equivalence if and only if

  $$\begin{aligned} \mathrm {Map}_{s\mathscr {S}^+}((Z,B),(W,W_{hoequiv})) \rightarrow \mathrm {Map}_{s\mathscr {S}^+}((Y,A),(W,W_{hoequiv})) \end{aligned}$$

  is a Kan equivalence for every complete Segal space W.

• 4. Finally, the model structure is given as a localization model structure of the unmarked CSS model structure. Hence, fibrations (weak equivalences) between fibrant objects are given by fibrations (weak equivalences) in the unmarked CSS model structure.

We can now use our results about the marked CSS model structure to observe various interesting Quillen equivalences.

Theorem 2.26

The following diagram

is a commutative diagram of Quillen equivalences. Here the top row has the Joyal and CSS model structure. The bottom row has the marked Joyal and marked CSS model structure.

Proof

First we show the diagram commutes. It suffices to observe that the left adjoints commute. Moreover, left adjoints commute with colimits and so it suffices to check on generators. However, both sides of the square map $\varDelta [n]$ to $F(n)^\flat$.

We now move on to prove all four are Quillen equivalences. By Theorem 1.23, we already know that $(p_1^*,i_1^*)$ is a Quillen equivalence. Similarly, by Theorem 2.22, we know that the left hand $((-)^\flat , \mathrm {Unm})$ is a Quillen equivalence. Hence we have to focus on the other two.

First we show that $((p_1^+)^*, (i_1^+)^*)$ is a Quillen adjunction. Evidently $(p_1^+)^*$ preserves cofibrations, which are just the monomorphisms. Hence, it suffices to prove that $(i_1^+)^*$ preserves fibrant objects and fibrations between fibrant objects. However, fibrant objects are of the form $(W,W_{hoequiv})$, where W is a complete Segal space. By direct computation, $(i_1^+)^*(W,W_{hoequiv}) = (i_1^*(W), i_1^*(W)_{hoequiv})$, where $i_1^*(W)$ is a quasi-category (Theorem 1.23). Moreover, fibrations between fibrant objects are just unmarked CSS fibrations (Theorem 2.25), which are, again by Theorem 1.23, taken to Joyal fibrations.

Next, we prove that $((p_1^+)^*, (i_1^+)^*)$ is a Quillen equivalence. We can extend our adjunction as follows:

By Theorem 2.25, $((t^+)_!,(t^+)^!)$ is a Quillen equivalence. Moreover, the composition $(t^+)_!(p_1^+)^*$ is just the identity and so is by default a Quillen equivalence. Hence, by 2-out-of-3, $((p_1^+)^*,(i_1^+)^*)$ is a Quillen equivalence.

Next, we show $((-)^\flat , \mathrm {Unm})$ is a Quillen adjunction. $(-)^\flat$ preserves cofibrations as they are just the monomorphisms. So,we only have to prove that $\mathrm {Unm}$ preserves fibrant objects and fibrations between fibrant objects. Similar to above, fibrant objects are just $(W,W_{hoequiv})$, where W is a complete Segal space and fibrations are just Reedy fibrations, both of which are preserves by $\mathrm {Unm}$.

Finally, we prove that $((-)^{\flat },\mathrm {Unm})$ is a Quillen equivalence. However, this follows immediately from the fact that the other three adjunctions are Quillen equivalences and 2-out-of-3.

Combining Theorem 2.25 and Theorem 2.26 with Proposition 1.10 gives us following useful corollary.

Corollary 2.27

Let (X, A) be a marked simplicial space and (S, B) be a marked simplicial set. We have following Quillen equivalences

Moreover, the adjunction $((t^+)_!,u^*(t^+)^!)$ is a simplicial Quillen equivalence.

Taking X to be the final object, the result above implies that we have constructed another model structure for $(\infty ,1)$-categories on the category of marked simplicial spaces.

Remark 2.28

We can summarize the results of this subsection with the following diagram of Quillen equivalences

The CSS model structure on the left hand side, $s\mathscr {S}^{CSS}$, and the marked Joyal model structure on the right hand side, $(s\mathscr {S}\text {et}^+)^{Joy^+}$, already existed and we build a bridge from one to the other by defining the marked CSS model structure, $(s\mathscr {S}^+)^{CSS^+}$.

So, what is the role of the unmarked CSS model structure,$(s\mathscr {S}^+)^{un^+CSS}$? If we wanted to directly construct a model structure on $s\mathscr {S}^+$ using the adjunction $((t^+)_!, (t^+)^!)$, we would have to left induce our model structure from the marked Joyal model structure. However, left-induced model structures are quite difficult to construct [22].

Hence, we used the unmarked CSS model structure, $(s\mathscr {S}^+)^{un^+CSS}$, as an intermediate step to avoid such difficulties. We can easily right induce this model structure from the CSS model structure, $s\mathscr {S}^{CSS}$ (as we did in Proposition 2.19). Now, as soon as we have any appropriate model structure on $s\mathscr {S}^+$, we can then use the theory of Bousfield localizations to get the desired marked CSS model structure, $(s\mathscr {S}^+)^{CSS^+}$. Thus, we can think of the unmarked CSS model structure as an intermediate step that allows us to easily define the marked CSS model structure.

We will use these adjunctions in the next subsection to define and study the Cartesian model structure of marked simplicial spaces.

3.3 Marked simplicial spaces vs. marked simplicial sets

In this section we define Cartesian fibrations of simplicial spaces and prove that we can define a model structure on marked simplicial spaces over a simplicial space such that the fibrant objects are precisely the Cartesian fibrations. We also show that this model structure is Quillen equivalent to the Cartesian model structure on marked simplicial sets via both adjunctions $((t^+)_!, (t^+)^!)$, $((p_1^+)^*, (i_1^+)^*)$.

First, we review the definition of Cartesian fibrations and Cartesian model structure of simplicial sets, as discussed in [31].

Definition 2.29

[31, Definition 2.4.1.1.] Let $p: T \rightarrow S$ be a map of simplicial sets. An edge $f:x \rightarrow y$ in T is p-Cartesian if

$$\begin{aligned} T_{/f} \twoheadrightarrow S_{/p(f)} \times _{S_{/p(y)}} T_{/y} \end{aligned}$$

is a trivial Kan fibration. Here, $T_{/y}$ is defined in [31, Proposition 1.2.9.2].

Definition 2.30

An inner fibration $p: T \rightarrow S$ is a Cartesian fibration, if for every edge $f: x \rightarrow y$ in S and lift $\tilde{y}$, there exist a p-Cartesian lift $\tilde{f}: \tilde{x} \rightarrow \tilde{y}$.

Cartesian fibrations are fibrant objects in a model structure on marked simplicial sets.

Theorem 2.31

[31, Proposition 3.1.3.7, Proposition 3.1.4.1, Corollary 3.1.4.4, Proposition 3.1.5.3] Let S be a simplicial set. There exists a unique left proper, combinatorial, simplicial model structure on $s\mathscr {S}\text {et}^+_{/S^\#}$ which may be described as follows:

C:

A map is a cofibration if the map of underlying simplicial sets is a monomorphism.

F:

Fibrant objects are of the form $(T,T^{Cart}) \rightarrow S^\#$, where $T \rightarrow S$ is a Cartesian fibration and $T^{Cart}$ the set of Cartesian edges.

W:

A morphism g is an equivalence if for every Cartesian fibration $T \rightarrow S$ the induced map $\mathrm {Map}_{/S}(g,T)$ is a Kan equivalence.

The simplicial enrichment is given by

$$\begin{aligned} \mathrm {Map}_{/S^\#}(T,U)_n = \mathrm {Hom}_{/S^\#}(T \times \varDelta [n]^\#,U). \end{aligned}$$

Finally, for every simplicial set S the adjunction

is a Quillen adjunction between the Joyal model structure and the Cartesian model structure.

Notation 2.32

In [31] a map of the form $(T,T^{Cart}) \rightarrow S^\#$ where $T \rightarrow S$ is a Cartesian fibration is denoted by $T^\natural$ over S, however, we will not use this notation.

Example 2.33

If $S=\varDelta [0]$ then the Cartesian model structure simply recovers the marked Joyal model structure introduced in Theorem 2.22.

Our goal is to define Cartesian fibrations of marked simplicial spaces and prove it comes with a model structure that is equivalent to the Cartesian model structure on marked simplicial sets.

Definition 2.34

A CSS fibration of simplicial spaces $Y \rightarrow X$ is a Cartesian fibration if $i_1^*Y \rightarrow i_1^*X$ is a Cartesian fibration of simplicial sets.

We now want to give an internal description of Cartesian fibrations of simplicial spaces, that does not rely on simplicial sets. This requires some category theory of simplicial spaces, as studied in [37].

Let X be a complete Segal space and f a morphism. Then the the complete Segal space of cones $X_{/f}$ [37, Definition 5.21] is defined as

$$\begin{aligned} X_{/f} = (X^{F(1)})^{F(1)} \underset{X^{F(1)} \times X^{F(1)}}{\times } X \times F(0). \end{aligned}$$

Generalizing from there, if X is an arbitrary simplicial space, then we can choose a complete Segal space fibrant replacement $X \rightarrow \hat{X}$ and define $X_{/f} = X \times _{\hat{X}} \hat{X}_{/f}$, using the fact that cocones are invariant under equivalences of complete Segal spaces [37, Theorem 5.1]. Note that, up to Reedy equivalence of simplicial spaces, this definition is independent of the choice of $\hat{X}$.

Definition 2.35

Let $p:V \rightarrow W$ be a CSS fibration of simplicial spaces. A morphism $f: x \rightarrow y$ in V is called p-Cartesian if the commutative square

is a homotopy pullback square of simplicial spaces.

We can now use this to give an internal characterization of Cartesian fibrations.

Lemma 2.36

Let $p: V \rightarrow W$ be CSS fibration. Then p is a Cartesian fibration if and only if for every morphism $f: x \rightarrow y$ in W and lift $\hat{y}$ in V of y, there exists a p-Cartesian morphism lift $\hat{f}$ of f (meaning $p(\hat{f}) = f$).

Proof

Before we start the proof, we recall that $i_1^*(W)_0 = W_{10}$, which means W and $i_1^*W$ have the same set of edges.

First, by Theorem 1.23, if $p: V \rightarrow W$ is a CSS fibration then $i_1^*(p): i_1^*(V) \rightarrow i_1^*(W)$ is a fibration in the Joyal model structure. Thus, by Definition 2.30, $i_1^*(p): i_1^*(V) \rightarrow i_1^*(W)$ is a Cartesian fibration of simplicial sets if and only if every edge $f: x \rightarrow y$ in $i_1^*(W)$ with given lift $\hat{y}$ has a $i_1^*(p)$-Cartesian lift.

Hence the statement follows immediately from proving that an edge f in V is p-Cartesian if and only if f in $i_1^*(V)$ is $i_1^*(p)$-Cartesian.

However, this follows from the fact that $i_1^*$ is a right Quillen functor of a Quillen equivalence and so

the right square is a homotopy pullback square if and only if the left hand square is a homotopy pullback square.

We now want to move our study of Cartesian fibrations into the marked world and so need an appropriate definition.

Definition 2.37

Let X be a simplicial space. We say a map of marked simplicial space $(Y,Y^{Cart}) \rightarrow X^\sharp$ is a Cartesian fibration if $Y \rightarrow X$ is a Cartesian fibration and $Y^{Cart}$ is the sub-space of Cartesian edges.

We are now ready to show that Cartesian fibrations (Definition 2.37) are fibrant objects in a model structure.

Theorem 2.38

Let X be a simplicial space. There is a unique combinatorial, left proper, simplicial model structure on $(s\mathscr {S}^+)_{/X^\#}$, called the Cartesian model structure and denoted $(s\mathscr {S}_{/X^\#})^{Cart}$, such that

• 1. Cofibrations are monomorphisms over $X^\#$.

• 2. Fibrant objects are Cartesian fibrations $(Y,Y^{Cart}) \rightarrow X^\#$.

• 3. A map is a weak equivalence if for every Cartesian fibration $(W,D) \rightarrow X^\sharp$ the induced map

  $$\begin{aligned} \mathrm {Map}_{/X^\sharp }((Z,C), (W,D)) \rightarrow \mathrm {Map}_{/X^\sharp }((Y,B), (W,D)) \end{aligned}$$

  is a Kan equivalence.

• 4. A map between Cartesian fibrations $(W,W^{Cart}) \rightarrow (V,V^{Cart}))$ over $X^\sharp$ is a weak equivalence (fibration) if and only if it is a weak equivalence (fibration) in the marked CSS model structure.

• 5. The adjunction

  

  is a simplicial Quillen equivalence.

Proof

Combining Corollary 2.27 and Theorem 2.31, we have simplicial Quillen adjunctions

between combinatorial simplicial model structures, where the right adjoint is fully faithful (by Corollary 2.27). Hence, by Theorem 1.9, we can define a new model structure on $s\mathscr {S}^+_{/X^\#}$, which we call the Cartesian model structure and that makes the adjunction $((t^+)_!,u^*(t^+)^!)$ into a simplicial Quillen equivalence.

Next, combining the facts that $(t^+)_!$ reflects cofibrations (Theorem 1.9) and that cofibrations in $((s\mathscr {S}\text {et}^+)_{/t_!X^\#})^{Cart}$ are monomorphisms implies that cofibrations in $((s\mathscr {S}^+)_{/X^\#})^{Cart}$ are also monomorphisms.

Next, we characterize the fibrant objects, which are precisely the fibrant objects in $(s\mathscr {S}^+_{/X})^{CSS^+}$ that are in the essential image of $u^*(t^+)^!$. By Theorem 2.26, if a map $(Y,B) \rightarrow X^\sharp$ is a marked CSS fibration, then $Y \rightarrow X$ is a CSS fibration of simplicial spaces. On the other hand, (Y, B) is in the image if $(Y,B) = (t^+)^*(C,C^{Cart}) = (t^!C, (t^!C)^{Cart})$, which implies that $B = Y^{Cart}$. Hence, the fibrant objects are precisely the Cartesian fibrations over $X^\#$.

The characterization of weak equivalences follows from the fact that the model structure is simplicial and that the fibrant objects are given by Cartesian fibrations of marked simplicial spaces.

Finally, the model structure is given as a localization model structure of the marked CSS model structure. Hence, fibrations (weak equivalences) between fibrant objects are given by fibrations (weak equivalences) in the marked CSS model structure.

We constructed the Cartesian model structure on $(s\mathscr {S}^+)_{/X}$ as a localization model structure. Hence, we get following result.

Corollary 2.39

Let X be a simplicial space. Then the adjunction

is a Quillen adjunction.

We end this section by giving a second Quillen equivalence between the Cartesian model structures.

Theorem 2.40

Let S be a simplicial set. The adjunction

is a Quillen equivalence between Cartesian model structures.

Proof

In order to prove it is a Quillen adjunction it suffices to show the left adjoint preserves cofibrations and the right adjoint preserves fibrant objects and trivial fibrations between fibrant objects. Evidently, $(p_1^+)^*$ preserves cofibrations as they are just monomorphisms.

Moreover, $(i_1^+)^*$ preserves trivial fibrations between fibrant objects. Indeed, by Theorem 2.38, weak equivalences between fibrant objects are just marked CSS equivalences, which, by Theorem 2.26, are mapped to marked Joyal equivalences, which, by Theorem 2.31, are Cartesian equivalences.

We are left with proving that $(i_1^+)^*$ preserves fibrant object. However, by Theorem 2.38, fibrant objects are of the form $(Y,Y^{Cart}) \rightarrow X^\sharp$, where $Y \rightarrow X$ is a Cartesian fibration. By direct computation, $(i_1^+)^*((Y,Y^{Cart}) \rightarrow X^\sharp ) = (i_1^*Y, i_1^*Y^{Cart}) \rightarrow i_1^*X^\sharp$, which is fibrant in the Cartesian model structure in $(s\mathscr {S}\text {et}^+_{/i_1^*X^\sharp })^{Cart}$ (Theorem 2.31).

We move on to prove that the adjunction is a Quillen equivalence. We can extend the adjunction above to the following diagram

The second adjunction is a Quillen equivalence by the previous theorem. The composition is the identity and so also a Quillen equivalence. Hence the left hand Quillen adjunction is a Quillen equivalence, by 2-out-of-3.

4 Equivalence of Cartesian model structures: model dependent and independent

Until this point we have studied many different model structures, that we all denoted by Cartesian model structure: for marked simplicial sets, marked simplicial spaces, bisimplicial sets and bisimplicial spaces. We are finally in a position where we can show that all these model structures are in fact Quillen equivalent via a zig–zag of Quillen equivalence and hence we are justified in giving all of them the same name.

Finally, in the last subsection, we show how this immediately gives us an equivalence of underlying quasi-categories, where we can replace a zig–zag of equivalences with direct adjoint equivalences.

4.1 Quillen equivalence of Cartesian model structures

In this section we want to prove that we have following diagram of Quillen equivalences (the direction of the arrows are the direction of the right adjoints). Here an arrow marks a right Quillen functor of a Quillen equivalence, X is a simplicial space and S a simplicial set.

• ${((t^+)_!,u^*(t^+)^!):}$ This is proven in Theorem 2.38.

• ${((p_1^+)^*,u^*(i_1^+)^*):}$ This is proven in Theorem 2.40.

• ${(st_!,su^*t^!):}$ This is proven in Theorem 1.35.

• ${(sp_1^*,su^*i_1^*):}$ This is proven in Theorem 1.35.

• ${(((t^+)_!)_* , ((t^+)^!)_*):}$ This follows from applying Lemma 1.6 to the Quillen equivalence $(((t^+)_!)_*,((t^+)_!)_*)$ (Theorem 2.25).

• ${(((-)^\flat )_* , (\mathrm {Unm})_*):}$ This follows from applying Lemma 1.6 to the Quillen equivalence $(((-)^\flat )_*,(\mathrm {Unm})_*)$ (Theorem 2.26).

• ${(\mathrm {sSt}_S,\mathrm {sUn}_S):}$ This follows from applying Theorem 1.21 to the Quillen equivalence $(\mathrm {St}_S,\mathrm {Un}_S)$ [31, Theorem 2.2.1.2].

• ${(\mathrm {St}_S^+,\mathrm {Un}_S^+):}$ This is the statement of [31, Theorem 3.2.0.1].

4.2 Equivalences of quasi-categories

The work here focused on model categorical formalism, but in this subsection we want to give short analysis of the quasi-categorical implications of this result. The model structures from Sect. 3.1 are all simplicial. So, we can apply the simplicial nerve N ([31, 1.1.5]) and the the fact that Quillen equivalences of simplicial model categories gives us adjoint equivalences of quasi-categories [31, Proposition 5.2.4.6], to get a diagram of equivalences of quasi-categories (here we only focus on the case over a simplicial space X):

By [43, 2.1.12], whenever we have an adjoint equivalence of quasi-categories, both functors are right and left adjoints. Thus we can ignore the direction of the arrows. This is clearly not true for Quillen equivalences of model categories, as functors (even equivalences) are usually not right and left Quillen.