Abstract
Using a suitable notion of normal Galois extension of commutative rings, we develop the relative theory of the generalized Teichmüller cocycle map. We interpret the theory in terms of the Deuring embedding problem, construct an eight term exact sequence involving the relative Teichmüller cocycle map and suitable relative versions of generalized Brauer groups and compare the theory with the group cohomology eight term exact sequence involving crossed pairs. We also develop somewhat more sophisticated versions of the ordinary, equivariant and crossed relative Brauer groups and show that the resulting exact sequences behave better with regard to comparison of the theory with group cohomology than do the naive notions of the generalized relative Brauer groups.
Similar content being viewed by others
1 Introduction
We explore further the approach to the “Teichmüller cocycle map” developed in [14] in terms of crossed 2-fold extensions. For intelligibility, we recall briefly the situation: Let S be a unitary commutative ring, Q a group that acts on S by ring automorphisms via a homomorphism \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\), and let R denote the subring of S that consists of the elements of S which are fixed under Q. A Q-normal S-algebra consists of a central S-algebra A and a homomorphism \(\sigma :Q\rightarrow {\text{ Out }}(A)\) into the group \({\text{ Out }}(A)\) of outer automorphisms of A that lifts the action of Q on S. With respect to the abelian group \(\mathrm U(S)\) of invertible elements of S, endowed with the Q-module structure coming from the Q-action on S, the Teichmüller complex of \((A, \sigma )\) associated to a Q-normal S-algebra \((A, \sigma )\) is a crossed 2-fold extension \(\mathrm {e}_{(A, \sigma )}\) starting at \(\mathrm U(S)\) and ending at Q, and this crossed 2-fold extension represents a class, the Teichmüller class of \((A, \sigma )\), in the third group cohomology group \(\mathrm H^3(Q,\mathrm U(S))\) of Q with coefficients in \(\mathrm U(S).\)
We now review rapidly the contents of the sections of the present paper. A more detailed introduction for the entire series that consists of [14], the present paper, and [15] can be found in the introduction to [14].
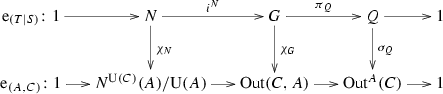
In Section 12 we introduce the concept of a Q-normal Galois extension of commutative rings; associated to such a Q-normal Galois extension T|S of commutative rings is a structure extension \(\mathrm {e}_{(T|S)}:N\rightarrowtail G \twoheadrightarrow Q\) of Q by the Galois group \(N={\text{ Aut }}(T|S)\) of T|S and an action \(G \rightarrow {\text{ Aut }}(T)\) of G on T by ring automorphisms. In Section 13 we associate to a crossed pair \((\mathrm {e}, \psi )\) with respect to \(\mathrm {e}_{(T|S)}\) and \(\mathrm U(T)\), endowed with the G-module structure coming from the G-action on T, see [13] or Section 13 below for details on the crossed pair concept, a Q-normal crossed product algebra \((A_\mathrm {e} , \sigma _\psi )\) which we refer to as a crossed pair algebra. The crossed pair algebra \((A_\mathrm {e} , \sigma _\psi )\) represents a member of the kernel \(\mathrm {XB}(T|S; G, Q)\) of the obvious homomorphism from \(\mathrm {XB}(S,Q)\) to \(\mathrm {XB}(T,G)\); this homomorphism exists and is unique, in view of the functoriality of the crossed Brauer group. The assignment to \((\mathrm {e} , \psi )\) of \((A_\mathrm {e}, \sigma _\psi )\) yields a natural homomorphism of abelian groups from the corresponding abelian group \(\mathrm {Xpext} (G,N;\mathrm U(T)) \) of congruence classes of crossed pairs introduced in [13] to the subgroup \(\mathrm {XB}(T|S;G,Q)\) of the crossed Brauer group.
Theorem 13.5 below says that a class \(k \in \mathrm H^3(Q, \mathrm U(S))\) is the Teichmüller class of some crossed pair algebra \((A_\mathrm {e} , \sigma _\psi )\) with respect to the data if and only if k is split in T|S in the sense that, under inflation \(\mathrm H^3(Q,\mathrm U(S)) \rightarrow \mathrm H^3(G,\mathrm U(T))\), the class k goes to zero. In Section 14, given a Q-normal Galois extension T|S of commutative rings, we again focus our attention on the Deuring embedding problem of a central T-algebra into a central S-algebra and establish two somewhat technical results, Theorems 14.9 and 14.10 below; these results entail, in particular that, if a class \(k \in \mathrm H^3(Q,\mathrm U(S))\) goes under inflation to the Teichmüller class in \(\mathrm H^3(G,\mathrm U(T))\) of some G-normal central T-algebra A, then k is itself the Teichmüller class of some Q-normal central S-algebra B in such a way that, when A is an Azumaya T-algebra, B may be taken to be an Azumaya S-algebra. Sections 15 and 16 are preparatory in character.
Given a Q-normal Galois extension T|S of commutative rings with associated structure extension \(\mathrm {e}_{(T|S)}:{\text{ Aut }}(T|S)\rightarrowtail G \twoheadrightarrow Q\) and G-action on T, we use the notation \(\mathrm {EB}(T|S;G,Q)\) for the kernel of the induced homomorphism from \(\mathrm {EB}(S,Q)\) to \(\mathrm {XB}(T,G)\); the exact sequence (17.2) below involving the Teichmüller map t now yields an extension of the kind
of the corresponding classical low degree four term exact sequence by four more terms. We refer to the resulting theory as the naive relative theory. In Theorem 18.1 we compare that exact sequence with the eight term exact sequence in the cohomology of the group extension \(\mathrm {e}_{(T|S)}\) with coefficients in \(\mathrm U(T)\) constructed in [13].
Finally, we develop a more sophisticated variant of the relative theory which behaves better with regard to comparison of the theory with group cohomology than does the naive relative theory; see Theorems 18.4–18.6 and 18.8.
The appendix recollects some material from the theory of stably graded symmetric monoidal categories. We keep the section numbering from [14].
2 Normal ring extensions
As in [14], S denotes a commutative ring and \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\) an action of a group Q on S. Let T|S be a Galois extension of commutative rings with Galois group \(N={\text{ Aut }}(T|S)\). We refer to T|S as being Q-normal when each automorphism \(\kappa _Q(q)\) of S, as q ranges over Q, extends to an automorphism of T.
Somewhat more formally, given a Galois extension T|S of commutative rings with Galois group N, denote by \({\text{ Aut }}^S(T)\) the group of those automorphisms of T that map S to itself, let \({\text{ res }}:{\text{ Aut }}^S(T) \rightarrow {\text{ Aut }}(S)\) denote the obvious restriction map, so that \(N={\text{ Aut }}(T|S)\) is the kernel of \({\text{ res }}\), let G denote the fiber product group \(G = {\text{ Aut }}^S(T) \times _{{\text{ Aut }}(S)} Q\) relative to \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\), and let \(\pi _Q :G \rightarrow Q\) denote the canonical homomorphism and \(i^N:N \rightarrow G\) the obvious injection. The obvious homomorphism \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\) makes the diagram

commutative, where the unlabeled arrow is the obvious homomorphism. This diagram is a special case of a diagram of the kind [14, (3.19)]. The Galois extension T|S of commutative rings is plainly Q-normal if and only if the homomorphism \(\pi _Q:G \rightarrow Q\) is surjective, that is, if and only if the sequence
is exact, i.e., an extension of Q by N. Given a Q-normal Galois extension T|S of commutative rings, we refer to the corresponding group extension (12.2) as the associated structure extension and to the corresponding homomorphism
as the associated structure homomorphism. It is immediate that a Q-normal Galois extension T|S with structure extension (12.2) and structure homomorphism
the injection \(S \subseteq T\) being denoted by \(i:S \subseteq T\), yields the morphism
in the change of actions category  introduced in [14, Subsection 3.7].
introduced in [14, Subsection 3.7].
Example 12.1
Let K|P be a Galois extension of algebraic number fields, and denote by G the Galois group of K|P. Let Z be a subfield of K that contains P and is a normal extension of P, and let \(N = {\text{ Gal }}(K|Z)\) and \(Q = {\text{ Gal }}(Z|P)\). Let T, S and R denote the rings of integers in, respectively, K, Z and P. Suppose that K|Z is unramified but that Z|P is ramified. Then T|S is a Q-normal Galois extension of commutative rings but T|R and S|R are not Galois extensions of commutative rings, cf. [14, Example 2.3].
Let \((S, Q, \kappa )\) and \((\hat{S}, \hat{Q}, \hat{\kappa })\) be objects of the change of actions category  introduced in [14, Subsection 3.7], and let T|S and \(\hat{T}|\hat{S}\) be normal Galois extension of commutative rings with respect to Q and \(\hat{Q}\), with structure extensions
introduced in [14, Subsection 3.7], and let T|S and \(\hat{T}|\hat{S}\) be normal Galois extension of commutative rings with respect to Q and \(\hat{Q}\), with structure extensions
and structure homomorphisms \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\) and \(\hat{\kappa }_G:\hat{G} \rightarrow {\text{ Aut }}^{\hat{S}}(\hat{T})\), respectively. Then a morphism
of normal Galois extensions consists of a ring homomorphism \(h :T \rightarrow \hat{T}\) and a group homomorphism \(\phi :\hat{G} \rightarrow G\) such that
-
(i)
\(f = h|S\) is a ring homomorphism \(S \rightarrow \hat{S}\),
-
(ii)
the values of \(\phi |\hat{N}\) lie in N, that is, \(\phi |\hat{N}\) is a homomorphism \(\hat{N} \rightarrow N\), and
-
(iii)
\(h ({}^{\phi (\hat{x})} t) = {}^{\hat{x}}(h(t)), \ \hat{x} \in \hat{G}, \ t\in T\).
3 Crossed pair algebras
As before, S denotes a commutative ring and \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\) an action of a group Q on S. In this section we use the results of [13] to offer a partial answer to the question as to which classes in \(\mathrm H^3(Q,\mathrm U(S))\) are Teichmüller classes. Our result extends the classical answer of Eilenberg–Mac Lane [5] (reproduced in [11]); later in the paper we shall give a complete answer.
3.1 Crossed pairs
For intelligibility, we recall that notion from [13, p. 152].
Let
be a group extension and M a G-module; we write the G-action \(G \times M \longrightarrow M\) on M as \((x,y) \mapsto {}^xy\), for \(x \in G\) and \(y \in M\). Further, let \(\mathrm {e} :M \rightarrowtail \varGamma \mathop {\twoheadrightarrow }\limits ^{\pi _N}N\) be a group extension whose class \([\mathrm {e}] \in \mathrm H^2 (N,M)\) is fixed under the standard Q-action on \(\mathrm H^2(N,M)\). Given \(x\in G\), we write
Write \({\text{ Aut }}_G(\mathrm {e}) \) for the subgroup of \({\text{ Aut }}(\varGamma ) \times G\) that consists of those pairs \((\alpha , x)\) which make the diagram

commutative.
The homomorphism
together with the obvious action of \({\text{ Aut }}_G(\mathrm {e} )\) on \(\varGamma \), yields a crossed module
whence, in particular, \(\beta (\varGamma )\) is a normal subgroup of \({\text{ Aut }}_G(\mathrm {e} )\); we denote by \({\text{ Out }}_G(\mathrm {e})\) the cokernel of \(\beta \) and write the resulting crossed 2-fold extension as
The map \(\mathrm {Der}(N,M) \longrightarrow {\text{ Aut }}_G(\mathrm {e})\) given by the association
is an injective homomorphism; this homomorphism and the obvious map
yield the group extension
the map \({\text{ Aut }}_G(\mathrm {e}) \rightarrow G\) being surjective, since the class \([\mathrm {e} ] \in \mathrm H^2 (N,M)\) is supposed to be fixed under Q. Further, let \(\zeta :M \rightarrow \mathrm {Der}(N,M)\) be the homomorphism defined by \((\zeta (m))(n)=m({}^nm)^{-1}\), as m ranges over M and n over N. With these preparations out of the way, the data fit into the commutative diagram

with exact rows and columns. We use the notation

for the bottom row extension of (13.3). This extension is the cokernel, in the category of group extensions with abelian kernel, of the morphism \((\zeta ,\beta ,i)\) of group extensions.
Suppose now that the extension \(\overline{\mathrm {e}}\) splits; we then say that \(\mathrm {e}\) admits a crossed pair structure, and we refer to a section \(\psi :Q \rightarrow {\text{ Out }}_G(\mathrm {e} )\) of \(\overline{\mathrm {e}}\) as a crossed pair structure on the group extension \(\mathrm {e}:M \rightarrowtail \varGamma \mathop {\twoheadrightarrow }\limits ^{\pi _N}N\) with respect to the group extension (13.1). By definition, a crossed pair \((\mathrm {e},\psi )\) with respect to the group extension (13.1) and the G-module M consists of a group extension \(\mathrm {e}:M \rightarrowtail \varGamma \twoheadrightarrow N\) whose class \([\mathrm {e}]\in \mathrm H^2(N,M)\) is fixed under Q such that the associated extension \(\overline{\mathrm {e}}\) splits, together with a section \(\psi :Q \rightarrow {\text{ Out }}_G(\mathrm {e} )\) of \(\overline{\mathrm {e}}\) [13, p. 152].
Suitable classes of crossed pairs with respect to (13.1) and the G-module M constitute an abelian group \(\mathrm {Xpext}(G,N; M)\) [13, Theorem 1]. Moreover, cf. [13, Theorem 2], suitably defined homomorphisms
yield an extension of the classical five term exact sequence to an eight term exact sequence of the kind
For later reference, we recall the construction of \(\varDelta \). To this end, given a crossed pair
with respect to the group extension (13.1) and the G-module M, let \(B^\psi \) denote the fiber product group \({\text{ Aut }}_G (\mathrm {e} ) \times _{{\text{ Out }}_G (\mathrm {e})} Q\) with respect to the crossed pair structure map \(\psi :Q \rightarrow {\text{ Out }}_G (\mathrm {e})\) and, furthermore, let \(\partial ^\psi :\varGamma \rightarrow B^\psi \) denote the obvious homomorphism; together with the obvious action of \(B^\psi \) on \(\varGamma \) induced by the canonical homomorphism \(B^\psi \rightarrow {\text{ Aut }}_G (\mathrm {e} )\), the exact sequence
is a crossed 2-fold extension and hence represents a class in \(\mathrm H^3(Q,M^N)\). We refer to \(\mathrm {e}_\psi \) as the crossed 2-fold extension associated to the crossed pair \((\mathrm {e},\psi )\). The homomorphism \(\varDelta :\mathrm {Xpext} (G,N;M) \rightarrow \mathrm H^3(Q,M^N)\) is given by the assignment to a crossed pair \((\mathrm {e},\psi )\) of its associated crossed 2-fold extension \(\mathrm {e}_\psi \).
Remark 13.1
By [12, Theorem 1], the association \(\mathrm {e} \mapsto \overline{\mathrm {e}}\) yields a conceptual description of the differential \(d_2 :\mathrm E^{0,2}_2 \rightarrow \mathrm E^{2,1}_2\) of the Lyndon-Hochschild-Serre spectral sequence \((\mathrm E^{p,q}_r,d_r)\) associated with the group extension (13.1) and the G-module M.
Proposition 13.2
In the special case where the N-action on M is trivial, given a group extension \(\mathrm {e}:M \rightarrowtail \varGamma \mathop {\twoheadrightarrow }\limits ^{\pi _N}N\) that admits a crossed pair structure, crossed pair structures \(\psi :Q \rightarrow {\text{ Out }}_G(\mathrm {e})\) on the group extension \(\mathrm {e}\) correspond bijectively to actions of G on \(\varGamma \) that turn \(i^N \circ \pi _N:\varGamma \rightarrow G\) into a crossed module in such a way that the canonical homomorphism \( G\rightarrow B^\psi ={\text{ Aut }}_G (\mathrm {e} ) \times _{{\text{ Out }}_G (\mathrm {e})} Q\) is an isomorphism. \(\square \)
Remark 13.3
Given the group extension (13.1), consider a group extension
the group X not necessarily being abelian, let \(\phi = i^N\circ \pi _N:K \rightarrow G\) denote the composite of i and \(\pi _N\), and let \({\text{ Aut }}(\mathrm {e}) \) denote the subgroup of \({\text{ Aut }}(K)\) that consists of the automorphisms of K that map X to itself; such a homomorphism \(\phi \) is referred to in [17] as a normal homomorphism. Conjugation in K yields a homomorphism \(\beta :K \rightarrow {\text{ Aut }}(\mathrm {e})\) from K onto a normal subgroup \(\beta (K)\) of \({\text{ Aut }}(\mathrm {e})\), and the restriction \(\zeta \) of \(\beta \) to X, that is, conjugation in K with elements of X, yields a homomorphism \(\zeta :X \rightarrow {\text{ Aut }}(\mathrm {e})\) from X onto a normal subgroup \(\zeta (X)\) of \({\text{ Aut }}(\mathrm {e})\) as well; let \(\mathrm {can}:{\text{ Aut }}(\mathrm {e})\rightarrow {\text{ Aut }}(\mathrm {e})/\zeta (X)\) denote the canonical surjection. A modular structure on \(\phi \) is a homomorphism \(\theta :G \rightarrow {\text{ Aut }}(\mathrm {e})/\zeta (X)\) making the diagram

commutative [17]. A pseudo-module is defined to be a pair \((\phi ,\theta )\) that consists of a normal homomorphism \(\phi \) and a modular structure \(\theta \) on \(\phi \) [17].
Let \((\phi ,\theta )\) be a pseudo-module and consider the two abstract kernels \({G \rightarrow {\text{ Out }}(X)}\) and \({Q\rightarrow {\text{ Out }}(K)}\) induced by that pseudo-module. Now, fix an abstract G-kernel structure \(\omega :G \rightarrow {\text{ Out }}(X)\) on X in advance and consider the group \({\text{ Aut }}_G(\mathrm {e})\) that consists of the pairs \((\alpha ,x)\in {\text{ Aut }}(\mathrm {e})\times G\) which make the diagram

commutative in such a way that the image of \(\alpha |X\) in \({\text{ Out }}(X)\) coincides with the value \(\omega (x) \in {\text{ Out }}(X)\). Then the modular structures on \(\phi \) that induce, in particular, the abstract G-kernel structure \(\omega \) on X are given by homomorphisms
In the special case where X is abelian, an abstract G-kernel structure on X is an ordinary G-module structure, and those modular structures \(\theta :G \rightarrow {\text{ Aut }}_G(\mathrm {e})/\zeta (X)\) correspond bijectively to crossed pair structures \(\psi :Q \rightarrow {\text{ Out }}_G(\mathrm {e})\) on \(\mathrm {e}\).
3.2 Crossed pairs and normal algebras
Let T|S be a Q-normal Galois extension of commutative rings, with structure extension

and structure homomorphism \( \kappa _G:G \rightarrow {\text{ Aut }}^S(T); \) in particular, the group N is finite. Let \(\left( \mathrm {e}:\mathrm U(T) \rightarrowtail \varGamma \twoheadrightarrow N, \ \psi :Q \rightarrow {\text{ Out }}_G(\mathrm {e} )\right) \) be a crossed pair with respect to the group extension \(\mathrm {e}_{(T|S)}\) and the G-module \(\mathrm U(T)\). The corresponding crossed 2-fold extension (13.2) now takes the form
To the crossed pair \((\mathrm {e}, \psi )\), we associate a Q-normal S-algebra \((A_\mathrm {e}, \sigma _\psi )\) as follows.
The composite \(\vartheta :\varGamma \rightarrow N \rightarrow {\text{ Aut }}(T)\) yields an action of \(\varGamma \) on T; let \(A_\mathrm {e} \) denote the crossed product algebra \((T,N, \mathrm {e}, \vartheta ).\) Since the group N is finite, \(A_\mathrm {e} \) is an Azumaya S-algebra; this fact also follows from [14, Proposition 5.4(xi)]. Recall that there is an obvious injection \(i :\varGamma \rightarrow \mathrm U(A_\mathrm {e}).\) The following is immediate.
Proposition 13.4
Setting
as t ranges over T, y over \(\varGamma \), and \((\alpha , x)\) over \({\text{ Aut }}_G(\mathrm {e} )\ (\subseteq {\text{ Aut }}(\varGamma ) \times G)\), we obtain a morphism
of crossed modules which, in turn, induces the morphism

of crossed 2-fold extensions, where \(i_\flat \) denotes the induced homomorphism.
Given a crossed pair \(\left( \mathrm {e}:0 \rightarrow \mathrm U(T) \rightarrow \varGamma \rightarrow N \rightarrow 1, \ \psi :Q \rightarrow {\text{ Out }}_G(\mathrm {e} )\right) \) with respect to the group extension \(\mathrm {e}_{(T|S)}\) and the G-module \(\mathrm U(T)\), let
it is then obvious that \((A_\mathrm {e} , \sigma _\psi )\) is a Q-normal (Azumaya) S-algebra, and we refer to \((A_\mathrm {e} , \sigma _\psi )\) as a Q-normal crossed pair algebra with respect to the Q-normal Galois extension T|S of commutative rings.
Theorem 13.5
Let T|S be a Q-normal Galois extension of commutative rings, with structure extension \(\mathrm {\mathrm {e}}_{(T|S)} :N\rightarrowtail G \twoheadrightarrow Q\) and structure homomorphism
cf. Section 12 above. Then a class \(k\in \mathrm H^3 (Q,\mathrm U(S))\) is the Teichmüller class of some crossed pair algebra \((A_\mathrm {e} , \sigma _\psi )\) with respect to the Q-normal Galois extension T|S if and only if k is split in T|S in the sense that k goes to zero under inflation
With \(M=\mathrm U(T)\) and \(M^N=\mathrm U(S)\), the theorem is a consequence of the exactness, at \(\mathrm H^3(Q,\mathrm U(S))\), of the sequence (13.4). Indeed, by construction, the homomorphism \(\varDelta \) is given by the assignment to a crossed pair
with respect to the group extension \(\mathrm {e}_{(T|S)}\) and the G-module \(\mathrm U(T)\) of the corresponding crossed 2-fold extension (13.5), which now takes the form
Theorem 13.5 is therefore a consequence of the following, which is again immediate.
Proposition 13.6
Given a crossed pair \((\mathrm {e}, \psi )\) with respect to the group extension \(\mathrm {e}_{(T|S)}\) and the G-module \(\mathrm U(T)\), the morphism \((i,i_{\sharp })\) of crossed modules in Proposition 13.4 above induces a congruence morphism

of crossed 2-fold extensions.
Proof of Theorem 13.5
By exactness, it is immediate that the Teichmüller class of any crossed pair algebra \((A_\mathrm {e} , \sigma _\psi )\) with respect to T|S is split in T|S. Hence the condition is necessary. To establish sufficiency, consider a class \(k\in \mathrm H^3 (Q,\mathrm U(S))\) which is split in T|S, that is, goes to zero under inflation
By exactness, k then arises from some crossed pair \((\mathrm {e}, \psi )\) with respect to the group extension \(\mathrm {e}_{(T|S)}\) and the G-module \(\mathrm U(T)\), that is,
By Proposition 13.6, the Teichmüller class of the associated crossed pair algebra \((A_\mathrm {e} , \sigma _\psi )\) with respect to T|S coincides with \([{\mathrm {e}}_{\psi }]=k\). \(\square \)
4 Normal Deuring embedding and Galois descent for Teichmüller classes
As before, S denotes a commutative ring and \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\) an action of a group Q on S. Let T|S be a Q-normal Galois extension of commutative rings, with structure extension
and structure homomorphism \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\), cf. (12.1). In this section, we prove, among others, that if a class \(k \in \mathrm H^3(Q,\mathrm U(S))\) goes under inflation to the Teichmüller class in \(\mathrm H^3(G,\mathrm U(T))\) of some G-normal T-algebra, then k is itself the Teichmüller class of some Q-normal S-algebra. To this end, we reexamine Deuring’s embedding problem, cf. [14, Subsection 4.9 and Section 6].
4.1 The definitions
Let A be a central T-algebra, \((C, \sigma _Q:Q \rightarrow {\text{ Out }}(C) )\) a Q-normal S-algebra, and \(A\subseteq C\) an embedding of A into C. We refer to the embedding of A into C as a Q-normal Deuring embedding with respect to \(\sigma _Q:Q \rightarrow {\text{ Out }}(C) \) and (14.1) if each automorphism \(\kappa _G(x)\) of T, as x ranges over G, extends to an automorphism \(\alpha \) of C in such a way that
-
(i)
\([\alpha ] = \sigma _Q (\pi _Q(x))\in {\text{ Out }}(C)\), and
-
(ii)
\(\alpha \) maps A to itself.
Remark 14.1
In the special case where Q is the trivial group, the group G boils down to the group \(N={\text{ Aut }}(S|R)\) and, since each automorphism \(\alpha \) of C that extends some \(x\in N\) is required to map A to itself and to map to the trivial element of \({\text{ Out }}(C)\), that automorphism \(\alpha \) necessarily extends to an inner automorphism of C that normalizes A; thus the notion of normal Deuring embedding then comes down to the notion of Deuring embedding introduced in [14, Subsection 4.9].
Remark 14.2
Given an embedding of A into C such that A coincides with the centralizer of T in C, an automorphism \(\alpha \) of C extending an automorphism \(\kappa _G(x)\) of T for \(x \in G\) necessarily maps A to itself. Thus, in the definition of a Q-normal Deuring embedding, condition (ii) is then redundant.
For technical reasons, we need a stronger concept of a normal Deuring embedding. We now prepare for this definition.
Let A be a central T-algebra, C a central S-algebra, and suppose the algebra A to be embedded into C. Recall the crossed module \((\mathrm U(C),{\text{ Aut }}(C), \partial _C)\) associated to the central S-algebra C, and consider the associated crossed 2-fold extension
cf. [14, (4.1)]. The normalizer \(N^{\mathrm U(C)}(A)\) of A in \(\mathrm U(C)\) and the centralizer \(C^{\mathrm U(C)}(T)\) of T in \(\mathrm U(C)\), together with \(\mathrm U(A)\) and \(\mathrm U(C)\), constitute an ascending sequence
of groups. When A coincides with the centralizer of T in C, the inclusion \(\mathrm U(A) \subseteq C^{\mathrm U(C)}(T)\) is the identity.
We continue with the general case where A does not necessarily coincide with the centralizer of T in C. Let \({\text{ Aut }}^A(C)\) denote the group of automorphisms of C that map A to itself. The action of \({\text{ Aut }}(C)\) on \(\mathrm U(C)\) induces an action of \({\text{ Aut }}^A(C)\) on each of the groups \(\mathrm U(A), C^{\mathrm U(C)}(T)\), and \(N^{\mathrm U(C)}(A)\), and the restrictions of the homomorphism \(\partial _C\) together with the actions yield three crossed modules
each homomorphism \(\partial ^N_C, \partial ^T_C, \partial ^A_C\) being the corresponding restriction of the homomorphism \(\partial _C:\mathrm U(C) \rightarrow {\text{ Aut }}(C)\). We write the associated crossed 2-fold extensions as
the groups \({\text{ Out }}(C,A), {\text{ Out }}(C,T)\), and \({\text{ Out }}^A(C)\) being defined by exactness. The inclusions \(\mathrm U(A) \subseteq C^{\mathrm U(C)}(T) \subseteq N^{\mathrm U(C)}(A)\) induce a commutative diagram

of morphisms of crossed 2-fold extensions and, by diagram chase, the induced homomorphisms \({\text{ Out }}(C,A) \rightarrow {\text{ Out }}(C,T)\) and \({\text{ Out }}(C,T)\rightarrow {\text{ Out }}^A(C)\) are surjective.
Restriction induces canonical homomorphisms
(where the notation “res” is slightly abused) in such a way that the diagram

is commutative. Moreover, the obvious homomorphism \({\text{ Out }}^A(C) \rightarrow {\text{ Out }}(C)\) is injective, and we identify \({\text{ Out }}^A(C)\) with its isomorphic image in \({\text{ Out }}(C)\) if need be.
Now, given a homomorphism \(\chi _G:G \rightarrow {\text{ Out }}(C,A)\), its composite with the restriction map \({\text{ res }}:{\text{ Out }}(C,A) \rightarrow {\text{ Out }}(A)\) yields a G-normal structure on A. However, in order for such a homomorphism to match the other data, in particular the given Q-normal structure \(\sigma _Q:Q \rightarrow {\text{ Out }}(C)\), we must impose further conditions. We now spell out the details.
Let \(\partial ^A_{C,\sharp }:\mathrm U(A)/\mathrm U(S) \rightarrow {\text{ Aut }}^A(C)\) denote the (injective) homomorphism induced by the crossed module structure map \(\partial ^A_C\) in the crossed module (14.5). The crossed modules (14.3) and (14.5) yield the commutative diagram

with exact rows and columns, the third row being defined by exactness. This third row is an ordinary group extension, and we denote it by
We define a strong Q-normal Deuring embedding of A into C with respect to the Q-normal structure \(\sigma _Q:Q \rightarrow {\text{ Out }}(C)\) and the structure extension (14.1) to consist of an embedding of A into C together with a homomorphism \(\chi _G:G \rightarrow {\text{ Out }}(C,A)\) that is compatible with the other data in the following sense:
-
The restriction \(\chi _N:N \rightarrow N^{\mathrm U(C)}(A)/\mathrm U(A)\) to \(N={\text{ Aut }}(T|S)\) of the homomorphism \(\chi _G\) turns the embedding of A into C into a strong Deuring embedding relative to the action \(\mathrm {Id}:N \rightarrow {\text{ Aut }}(T|S)\) of N on T in such a way that the diagram
 (14.10)
(14.10)is commutative.
-
The composite
$$\begin{aligned} G \mathop {\longrightarrow }\limits ^{\chi _G}{\text{ Out }}(C,A)\mathop {\longrightarrow }\limits ^{\mathrm {res}}{\text{ Aut }}^S(T) \end{aligned}$$(14.11)coincides with \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\).
Remark 14.3
In the special case where Q is the trivial group, this notion of strong normal Deuring embedding comes down to the notion of strong Deuring embedding introduced in [14, Subsection 4.9].
Given a strong Q-normal Deuring embedding \((A\subseteq C,\chi _G)\) with respect to the Q-normal structure \(\sigma _Q:Q \rightarrow {\text{ Out }}(C)\) and to the group extension (14.1), the composite of \(\chi _G\) with the restriction map \({\text{ res }}:{\text{ Out }}(C,A) \rightarrow {\text{ Out }}(A)\) yields a G-normal structure
on A relative to the action \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\) of G on T; we refer to this structure as being associated to the strong Q-normal Deuring embedding.
4.2 Discussion of the notion of normal Deuring embedding
Recall that G denotes the fiber product group \({{\text{ Aut }}^S(T) \times _{{\text{ Aut }}(S)} Q}\) relative to the action \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\) of Q on S, that \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\) is the associated obvious homomorphism, and that \(\kappa _G\), restricted to N, boils down to the identity \(N \rightarrow {\text{ Aut }}(T|S)\), cf. (12.1) above.
Let A be a central T-algebra, consider an embedding of A into a central S-algebra C, and let \(\sigma _Q:Q \rightarrow {\text{ Out }}(C)\) be a Q-normal structure on C. Consider the fiber product group \(B^{A,\sigma _Q} ={\text{ Aut }}^A(C)\times _{{\text{ Out }}(C)} Q\) relative to the Q-normal structure \(\sigma _Q\) on C. The following is immediate.
Proposition 14.4
Abstract nonsense identifies the kernel of the canonical homomorphism \(B^{A,\sigma _Q} \rightarrow Q\) with the normal subgroup \(\mathrm {IAut}^A(C)\) of \({\text{ Aut }}^A(C)\) that consists of the inner automorphisms of C that map A to itself. Consequently the data determine a crossed module \((N^{\mathrm U(C)}(A), B^{A,\sigma _Q}, \partial ^{A,\sigma _Q})\), the requisite action of \(B^{A,\sigma _Q}\) on \(N^{\mathrm U(C)}(A)\) being induced from the canonical homomorphism \(B^{A,\sigma _Q} \rightarrow {\text{ Aut }}^A(C)\), in such a way that the sequence

is exact. \(\square \)
Since \(G ={{\text{ Aut }}^S(T) \times _{{\text{ Aut }}(S)} Q}\) (relative to the action \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\) of Q on S), and since the composite  coincides with the structure map \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\), by abstract nonsense, the combined homomorphism
coincides with the structure map \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\), by abstract nonsense, the combined homomorphism
and the canonical homomorphism \(\mathrm {can}:B^{A,\sigma _Q} \rightarrow Q\) induce a homomorphism
The following is again immediate.
Proposition 14.5
The embedding of A into C is a Q-normal Deuring embedding with respect to the Q-normal structure \(\sigma _Q :Q \rightarrow {\text{ Out }}(C)\) on C and the group extension (14.1) if and only if the homomorphism \(\pi _G:B^{A,\sigma _Q} \rightarrow G\) is surjective. \(\square \)
Whether or not the homomorphism \(\pi _G\) is surjective, we now determine the kernel of \(\pi _G\). To this end, let \({\text{ Aut }}^A(C|T)\) denote the subgroup of \({\text{ Aut }}^A(C)\) that consists of the automorphisms in \({\text{ Aut }}^A(C)\) that are the identity on T. Since T coincides with the center of A, restriction induces a homomorphism from \({\text{ Aut }}^A(C)\) to \({\text{ Aut }}(T)\), and since S coincides with the center of C, the values of this restriction map lie in the subgroup \({\text{ Aut }}^S(T)\) of \({\text{ Aut }}(T)\) that consists of the automorphisms of T which map S to itself. Thus, all told, restriction yields an exact sequence

of groups.
Consider the fiber product groups
relative to the homomorphisms \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\) and \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\), respectively, and let \(\mathrm {can}:B^{A,\kappa _G} \rightarrow G\) denote the canonical homomorphism. Since G is the fiber product group \({{\text{ Aut }}^S(T) \times _{{\text{ Aut }}(S)} Q}\) with respect to the homomorphism
by abstract nonsense, the canonical homomorphism from \(B^{A,\kappa _G}\) to \(B^{A,\kappa _Q}\) is an isomorphism. Moreover, the exact sequence (14.15) induces an exact sequence

of groups in such a way that

is a commutative diagram with exact rows.
Abstract nonsense yields a canonical homomorphism
and hence a canonical homomorphism \(B^{A,\sigma _Q} \rightarrow B^{A,\kappa _G}\) whose composite
with \(\mathrm {can}:B^{A,\kappa _G}\rightarrow G\) coincides with \(\pi _G:B^{A,\sigma _Q} \rightarrow G\).
Proposition 14.6
(i) The homomorphism \(B^{A,\sigma _Q} \rightarrow B^{A,\kappa _G}\) is injective.
(ii) Under the identification of \(B^{A,\sigma _Q}\) with its isomorphic image in the group \(B^{A,\kappa _G}\), the group \({\text{ Aut }}^A(C|T)\) being identified with its isomorphic image in \(B^{A,\kappa _G}\) via (14.16), the kernel of \(\pi _G:B^{A,\sigma _Q} \rightarrow G\) gets identified with the normal subgroup of \({\text{ Aut }}^A(C|T)\) that consists of the automorphisms in \({\text{ Aut }}^A(C|T)\) that are inner automorphisms of C.
(iii) Consequently the canonical homomorphism from the centralizer \(C^{\mathrm U(C)}(T)\) of T in \(\mathrm U(C)\) to \({\text{ Aut }}^A(C|T)\) yields a surjective homomorphism
Proof
Since the canonical homomorphism \(B^{A,\kappa _G} \rightarrow B^{A,\kappa _Q}\) is an isomorphism, the right-hand square in the the commutative diagram

is a pull back square, and hence inspection of the diagram reveals that the homomorphism  is injective. This establishes (i).
is injective. This establishes (i).
To justify (ii), we note first that the kernel of \({\text{ Aut }}^A(C)\rightarrow {\text{ Out }}(C)\) is the normal subgroup \(\mathrm {IAut}^A(C)\) of \({\text{ Aut }}^A(C)\) that consists of the inner automorphisms of C that map A to itself. Since the group \(B^{A,\sigma _Q}\) is the fiber product group \(B^{A,\sigma _Q} ={\text{ Aut }}^A(C)\times _{{\text{ Out }}(C)} Q\), abstract nonsense identifies the kernel of the canonical homomorphism \(B^{A,\sigma _Q} \rightarrow Q\) with \(\mathrm {IAut}^A(C)\), and it is immediate that \(\mathrm {ker}(\pi _G)\) is a subgroup of \(\mathrm {IAut}^A(C)=\mathrm {ker}(B^{A,\sigma _Q} \rightarrow Q)\). On the other hand, \(B^{A,\sigma _Q}\) being identified with the corresponding subgroup of \(B^{A,\kappa _G}\), the kernel of \(\pi _G:B^{A,\sigma _Q} \rightarrow G\) gets identified with the intersection \(B^{A,\sigma _Q} \cap {\text{ Aut }}^A(C|T) \subseteq B^{A,\kappa _G}\) and hence with the intersection
Consequently the kernel of the homomorphism \(\pi _G\) gets identified with the normal subgroup of \({\text{ Aut }}^A(C|T)\) that consists of the automorphisms in \({\text{ Aut }}^A(C|T)\) that are inner automorphisms of C.
Finally, statement (iii) is an immediate consequence of (ii). \(\square \)
Proposition 14.7
Suppose that the embedding of A into C is a Q-normal Deuring embedding with respect to the Q-normal structure \(\sigma _Q :Q \rightarrow {\text{ Out }}(C)\) on C and the group extension (14.1).
(i) The surjective homomorphism (14.14) yields a crossed 2-fold extension

(ii) The values of the Q-normal structure \(\sigma _Q:Q \rightarrow {\text{ Out }}(C)\) on C lie in the subgroup \({\text{ Out }}^A(C) (=\mathrm {coker}( {\partial ^N_C}:N^{\mathrm U(C)}(A) \longrightarrow {\text{ Aut }}^A(C)) \), cf. (14.8)).
Proof
Statement (i) is an immediate consequence of Propositions 14.5 and 14.6 (iii). Moreover, the diagram

is commutative and, in view of Proposition 14.5, the canonical homomorphism from  to Q is surjective. Consequently the values of \(\sigma _Q:Q \rightarrow {\text{ Out }}(C)\) on C lie in the subgroup \({\text{ Out }}^A(C) (=\mathrm {coker}({\partial ^N_C}:N^{\mathrm U(C)}(A) \longrightarrow {\text{ Aut }}^A(C)))\). \(\square \)
to Q is surjective. Consequently the values of \(\sigma _Q:Q \rightarrow {\text{ Out }}(C)\) on C lie in the subgroup \({\text{ Out }}^A(C) (=\mathrm {coker}({\partial ^N_C}:N^{\mathrm U(C)}(A) \longrightarrow {\text{ Aut }}^A(C)))\). \(\square \)
Given a Q-normal Deuring embedding of A into C with respect to the Q-normal structure \(\sigma _Q :Q \rightarrow {\text{ Out }}(C)\) on C and the group extension (14.1), in view of Proposition 14.7(ii), let

denote the associated crossed 2-fold extension induced from (14.8) via the Q-normal structure \({\sigma _Q:Q \rightarrow {\text{ Out }}^A(C)}\) on C; the underlying sequence of groups and homomorphisms plainly coincides with (14.13). Recall that the Teichmüller complex \(\mathrm {e}_{(C,\sigma _Q)}\) of the kind [14, (4.7)] associated to the Q-normal S-algebra \((C,\sigma _Q)\) is the crossed 2-fold extension

induced from (14.2) via the Q-normal structure  on C. The following is again immediate.
on C. The following is again immediate.
Proposition 14.8
Suppose that the embedding of A into C is a Q-normal Deuring embedding with respect to the Q-normal structure \(\sigma _Q :Q \rightarrow {\text{ Out }}(C)\) on C and the group extension (14.1).
(i) The inclusion maps \(N^{\mathrm U(C)}(A) \rightarrow \mathrm U(C)\) and \(B^{A,\sigma _Q} \rightarrow B^{\sigma _Q}\) yield a congruence

of crossed 2-fold extensions from the crossed 2-fold extension (14.18) to the crossed 2-fold extension (14.19).
(ii) The injection \(C^{\mathrm U(C)}(T) \rightarrow N^{\mathrm U(C)}(A)\) yields the morphism

of crossed 2-fold extensions from the crossed 2-fold extension (14.17) to the crossed 2-fold extension (14.18). \(\square \)
4.3 Results related with the two notions of normal Deuring embedding
Theorem 14.9
Let A be a central T-algebra, C a central S-algebra, and \(A \subseteq C\) an embedding of A into C having the property that A coincides with the centralizer of T in C. Furthermore, let \(\sigma _Q :Q \rightarrow {\text{ Out }}(C)\) be a Q-normal structure on C, and suppose that the embedding of A into C is a Q-normal Deuring embedding with respect to \(\sigma _Q\) and the group extension (14.1). Then the data determine a unique homomorphism \(\chi _G :G \rightarrow {\text{ Out }}(C,A)\) that turns the given Q-normal Deuring embedding of A into C into a strong Q-normal Deuring embedding of A into C with respect to the given data in such a way that, relative to the associated G-normal structure
on A, cf. (14.12),
Proof
Recall that the Teichmüller complex \(\mathrm {e}_{(C,{\sigma _Q} )}\) of the Q-normal S-algebra \((C,{\sigma _Q} )\), spelled out above as (14.19), represents the Teichmüller class
of the Q-normal central S-algebra \((C,{\sigma _Q})\).
Suppose that the embedding of A into C is a Q-normal Deuring embedding with respect to the Q-normal structure \(\sigma _Q :Q \rightarrow {\text{ Out }}(C)\) on C and the group extension (14.1). By Proposition 14.8(i), the crossed 2-fold extension \({\mathrm {e}}^A_{(C,\sigma _Q)}\), cf. (14.18), is available and is congruent to \({\mathrm {e}}_{(C,\sigma _Q)}\), whence
Moreover, by Proposition 14.8(ii), the crossed 2-fold extension (14.17) is available and, since the centralizer of A in C coincides with T, the inclusion \(\mathrm U(A)\subseteq C^{\mathrm U(C)}(T)\) identifies the group \(\mathrm U(A)\) of invertible elements of A with the centralizer \(C^{\mathrm U(C)}(T)\) of T in \(\mathrm U(C)\). Hence the crossed 2-fold extension (14.17) has the form

and the injection \(\iota :\mathrm U(A) \rightarrow N^{\mathrm U(C)}(A)\) induces the morphism (14.21) of crossed 2-fold extensions in Proposition 14.8(ii); this is a morphism of crossed 2-fold extensions of the kind \((1,\iota ,1,\pi _Q):{\mathrm {e}}^{A,T}_{(C,\sigma _Q)} \rightarrow {\mathrm {e}}^A_{(C,\sigma _Q)}\).
Denote by \(i :\mathrm U(S) \rightarrow \mathrm U(T)\) the inclusion. The canonical homomorphism
induces a morphism
of crossed modules and hence a homomorphism \(\chi _G :G \rightarrow {\text{ Out }}(C,A)\) such that

is a morphism of crossed 2-fold extensions from (14.22) to [14, (4.1)]. The homomorphism \(\chi _G\) turns the given Q-normal Deuring embedding of C into A into a strong Q-normal Deuring embedding of C into A with respect to the given data.
The G-normal structure \(\sigma _G:G \mathop {\rightarrow }\limits ^{\chi _G}{\text{ Out }}(C,A)\mathop {\rightarrow }\limits ^{{\text{ res }}}{\text{ Out }}(A)\) associated to the strong Q-normal Deuring embedding, in turn, induces a morphism

of crossed 2-fold extensions from (14.22) to the corresponding crossed 2-fold extension \(\mathrm {e}_{(A,\sigma _G)}\) of the kind [14, (4.7)]. Consequently \([\mathrm {e}_{(A,\sigma _G)}] = \inf [{\mathrm {e}}_{(C,{\sigma _Q})}]\). \(\square \)
Theorem 14.9 has a converse; this converse sort of a characterizes the Teichmüller classes in \(\mathrm H^3(Q,\mathrm U(S))\).
Theorem 14.10
Let \(k \in \mathrm H^3(Q,\mathrm U(S))\), let A be a central T-algebra, and let

be a G-normal structure on A relative to the action \( \kappa _G:G \rightarrow {\text{ Aut }}^S(T) \) of G on T. Suppose that

Then there is a Q-normal S-central crossed product algebra
related with the other data in the following way.
-
The Q-normal algebra \((C,\sigma _Q)=((A,N,\mathrm {e},\vartheta ),\sigma _Q )\) has Teichmüller class k;
-
once the Q-normal algebra \(((A,N,\mathrm {e},\vartheta ),\sigma _Q )\) has been fixed, the data determine a homomorphism \(\chi _G:G \rightarrow {\text{ Out }}(C,A)\) that turns the obvious embedding of A into \((A,N,\mathrm {e}, \vartheta )\) into a strong Q-normal Deuring embedding with respect to
$$\begin{aligned} \sigma _Q :Q \longrightarrow {\text{ Out }}(A,N,\mathrm {e}, \vartheta ) \end{aligned}$$and the group extension (14.1);
-
the associated G-normal structure
$$\begin{aligned} G \mathop {\longrightarrow }\limits ^{\chi _G}{\text{ Out }}(C,A) \mathop {\longrightarrow }\limits ^{{\text{ res }}}{\text{ Out }}(A) \end{aligned}$$on A, cf. (14.12), and the given G-normal structure
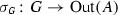 on A coincide.
on A coincide.
Complement 14.11
In the situation of Theorem 14.10, if A is an Azumaya T-algebra, the algebra \((A,N,\mathrm {e}, \vartheta )\) is an Azumaya S-algebra.
Remark 14.12
In the special case where \(\inf (k) = 0\), the argument to be given comes down to that given for the statement of Theorem 13.5, and this theorem is in fact a special case of Theorem 14.10.
Proof of Theorem 14.10
For convenience, we split the reasoning into Propositions 14.13–14.15 below.
Consider a G-normal central T-algebra  , and denote by
, and denote by  the restriction of
the restriction of  to N so that
to N so that  is an N-normal central T-algebra. The obvious unlabeled vertical arrow and the injection \(i^N\) turn
is an N-normal central T-algebra. The obvious unlabeled vertical arrow and the injection \(i^N\) turn

into a commutative diagram having as its rows the (exact) Teichmüller complexes  and
and  of
of  and
and  , respectively. Consequently the combined homomorphism
, respectively. Consequently the combined homomorphism

yields a group extension

Let

and

be the obvious group extensions so that splicing them yields the Teichmüller complex

of \(.\) We denote the resulting morphism

of group extensions by \(\varPhi \).
Consider the Teichmüller complex

associated to the given G-normal structure  on A, cf. [14, (4.7)]. Since \(\mathrm U(T)\) is a central subgroup of \(\mathrm U(A)\), the group extension \(\hat{\mathrm {e}}\) spelled out above as (14.24) is a central extension and, as noted in Proposition 13.2, G-crossed pair structures on \(\hat{\mathrm {e}}\) are equivalent to
on A, cf. [14, (4.7)]. Since \(\mathrm U(T)\) is a central subgroup of \(\mathrm U(A)\), the group extension \(\hat{\mathrm {e}}\) spelled out above as (14.24) is a central extension and, as noted in Proposition 13.2, G-crossed pair structures on \(\hat{\mathrm {e}}\) are equivalent to  -actions on \(\mathrm U(A)\) that turn
-actions on \(\mathrm U(A)\) that turn  into a crossed module. Thus the action of
into a crossed module. Thus the action of  on \(\mathrm U(A)\) that results from the given G-normal structure
on \(\mathrm U(A)\) that results from the given G-normal structure  via the associated crossed 2-fold extension
via the associated crossed 2-fold extension  induces a crossed pair structure
induces a crossed pair structure  on \(\hat{\mathrm {e}}\) with respect to the group extension
on \(\hat{\mathrm {e}}\) with respect to the group extension  and the G-module \(\mathrm U(T)\). Then the canonical homomorphism
and the G-module \(\mathrm U(T)\). Then the canonical homomorphism  yields a morphism
yields a morphism

of crossed 2-fold extensions such that the composite

coincides with  .
.
Proposition 14.13
Let \(k \in \mathrm H^3(Q,\mathrm U(S))\), let  be a G-normal central T-algebra, and suppose that
be a G-normal central T-algebra, and suppose that  . Then there is a group extension
. Then there is a group extension

together with a crossed pair structure  on \(\tilde{\mathrm {e}}\) with respect to the group extension (14.23) and the
on \(\tilde{\mathrm {e}}\) with respect to the group extension (14.23) and the  -module \(\mathrm U(T)\), the requisite module structure being induced by the map
-module \(\mathrm U(T)\), the requisite module structure being induced by the map  in
in  , related with the other data in the following way, where \(B^{\tilde{\psi }}\) denotes the fiber product group
, related with the other data in the following way, where \(B^{\tilde{\psi }}\) denotes the fiber product group  with respect to \(.\)
with respect to \(.\)
(i) The crossed 2-fold extension
associated to the crossed pair \((\tilde{\mathrm {e}},\tilde{\psi })\), cf. (13.5), represents k.
(ii) Relative to the obvious actions of the group  on the groups
on the groups  and N, the extension group \(\varGamma \) in \(\tilde{\mathrm {e}}\) fits into a commutative diagram of
and N, the extension group \(\varGamma \) in \(\tilde{\mathrm {e}}\) fits into a commutative diagram of  -groups with exact rows and columns as follows:
-groups with exact rows and columns as follows:

Proof
By [13, Theorem 2], the morphism (14.25) of group extensions induces a morphism for the corresponding eight term exact sequences in group cohomology constructed in [13]. In particular, \(\varPhi \) induces the commutative diagram

By the construction of \(\varDelta \), cf. Subsection 13.1 above or [13, Subsection 1.2],

and so, by exactness,  goes to zero in
goes to zero in  . Therefore k goes to zero in
. Therefore k goes to zero in  , and hence there is a group extension
, and hence there is a group extension

of the asserted kind together with a crossed pair structure  on \(\tilde{\mathrm {e}}\) with respect to the group extension (14.23) and the
on \(\tilde{\mathrm {e}}\) with respect to the group extension (14.23) and the  -module \(\mathrm U(T)\) whose
-module \(\mathrm U(T)\) whose  -module structure is induced by the projection
-module structure is induced by the projection  in
in  so that
so that
moreover, making a suitable choice of \((\tilde{\mathrm {e}}, \tilde{\psi })\) by means of some diagram chase if need be, we can arrange for \([(\tilde{\mathrm {e}}, \tilde{\psi })]\) to go to \([(\hat{\mathrm {e}}, \hat{\psi })]\) in the sense that

The crossed pair \((\tilde{\mathrm {e}}, \tilde{\psi })\) has the asserted properties. For \(\varDelta [(\tilde{\mathrm {e}}, \tilde{\psi })] = [{\mathrm {e}}_{\tilde{\psi }}]\) by definition, and so assertion (i) holds. Moreover, since \(\varPhi ^*[(\tilde{\mathrm {e}}, \tilde{\psi })] = [(\hat{\mathrm {e}}, \hat{\psi })]\), assertion (ii) holds as well. The details are as follows, cf. [13, Subsection 2.2].
Since \(\varPhi ^*[(\tilde{\mathrm {e}}, \tilde{\psi })] = [(\hat{\mathrm {e}}, \hat{\psi })]\), we may identify \((\hat{\mathrm {e}} , \hat{\psi })\) with the induced crossed pair \((\tilde{\mathrm {e}} \varPhi , \tilde{\psi }^\varPhi )\), cf. [13]. Recall that \(\tilde{\mathrm {e}}\varPhi \) is the group extension induced from \(\tilde{\mathrm {e}}\) via the injective homomorphism  and let \(\mathrm U =\ker (\varGamma \longrightarrow N)\); since \(\phi \) identifies \(\mathrm U(A)/\mathrm U(T)\) with the kernel of
and let \(\mathrm U =\ker (\varGamma \longrightarrow N)\); since \(\phi \) identifies \(\mathrm U(A)/\mathrm U(T)\) with the kernel of  , we can write the induced group extension \(\tilde{\mathrm {e}}\varPhi \) as
, we can write the induced group extension \(\tilde{\mathrm {e}}\varPhi \) as
To explain the induced crossed pair structure  , we note first that the injection \(\mathrm U \rightarrow \varGamma \) induces a morphism
, we note first that the injection \(\mathrm U \rightarrow \varGamma \) induces a morphism

of crossed 2-fold extensions. Moreover, restriction of the operators on \(\varGamma \) to \(\mathrm U\) yields a homomorphism

and this homomorphism, in turn, yields a morphism

of crossed 2-fold extensions. The crossed pair structure  is the composite
is the composite

of \({{\text{ res }}_{\flat }}\) with the canonical lift of the crossed pair structure  on \(\tilde{\mathrm {e}}\) to a homomorphism
on \(\tilde{\mathrm {e}}\) to a homomorphism  see [13, Propositions 2.3 and 2.4]. The identity \(\varPhi ^*[(\tilde{\mathrm {e}}, \tilde{\psi })] = [(\hat{\mathrm {e}}, \hat{\psi })]\) means that the two crossed pairs \((\hat{\mathrm {e}} , \hat{\psi })\) and \((\tilde{\mathrm {e}} \varPhi , \tilde{\psi }^\varPhi )\) are congruent as crossed pairs. Thus we may take \(\mathrm U\) to be \(\mathrm U(A)\) such that the following hold:
see [13, Propositions 2.3 and 2.4]. The identity \(\varPhi ^*[(\tilde{\mathrm {e}}, \tilde{\psi })] = [(\hat{\mathrm {e}}, \hat{\psi })]\) means that the two crossed pairs \((\hat{\mathrm {e}} , \hat{\psi })\) and \((\tilde{\mathrm {e}} \varPhi , \tilde{\psi }^\varPhi )\) are congruent as crossed pairs. Thus we may take \(\mathrm U\) to be \(\mathrm U(A)\) such that the following hold:
-
The injection \(\mathrm U(A) \rightarrow \varGamma \) induces a morphism \(\hat{\mathrm {e}} \rightarrow \tilde{\mathrm {e}}\) of group extensions whose restriction to \(\mathrm U(T)\) is the identity, as displayed in diagram (14.27) above, and
-
the crossed pair structure
 on \(\hat{\mathrm {e}}\) is the composite
on \(\hat{\mathrm {e}}\) is the composite  (14.28)
(14.28)of \(\tilde{\psi }_G\) with the homomorphism
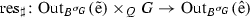 induced by the obvious restriction homomorphism
induced by the obvious restriction homomorphism 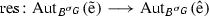 .
.
The morphism \(\hat{\mathrm {e}}\rightarrow \tilde{\mathrm {e}}\) of group extensions yields the commutative diagram (14.27) and, by construction, this is a commutative diagram of  -groups. \(\square \)
-groups. \(\square \)
We continue the proof of Theorem 14.10. Maintaining the hypotheses of Proposition 14.13, we write
for the group extension that arises as the middle column of diagram (14.27) and denote by \(\vartheta :\varGamma \rightarrow {\text{ Aut }}(A)\) the combined homomorphism

Consider the crossed product algebra \((A,N,\mathrm {e},\vartheta )\). By construction
cf. [14, Section 5]. By [14, Proposition 5.3(iv)], since T|S is a Galois extension of commutative rings with Galois group N, the group \(\varGamma \) now gets identified with the normalizer \(N^{\mathrm U(A,N,\mathrm {e},\vartheta )}(A)\) of A in the crossed product algebra \((A,N,\mathrm {e},\vartheta )\).
Recall the notation  for the fiber product group \({{\text{ Aut }}(A) \times _{{\text{ Out }}(A)}G }\) with respect to the given G-normal structure
for the fiber product group \({{\text{ Aut }}(A) \times _{{\text{ Out }}(A)}G }\) with respect to the given G-normal structure  on A, cf. [14, Subsection 4.4]. Furthermore, recall from Subsection 13.1 above that
on A, cf. [14, Subsection 4.4]. Furthermore, recall from Subsection 13.1 above that  denotes the subgroup of
denotes the subgroup of  that consists of the pairs \((\alpha , x)\) which render the diagram
that consists of the pairs \((\alpha , x)\) which render the diagram

commutative; here, given  , the notation
, the notation  refers to conjugation by
refers to conjugation by  and \(\ell _x:\mathrm U(T)\rightarrow \mathrm U(T)\) to the canonical action of
and \(\ell _x:\mathrm U(T)\rightarrow \mathrm U(T)\) to the canonical action of  on \(\mathrm U(T)\) (recall that T denotes the center of A) induced from the action of
on \(\mathrm U(T)\) (recall that T denotes the center of A) induced from the action of  on A and hence on \(\mathrm U(T)\) via the canonical homomorphism
on A and hence on \(\mathrm U(T)\) via the canonical homomorphism  .
.
Proposition 14.14
Setting
where  , we obtain a homomorphism
, we obtain a homomorphism

and this homomorphism, in turn, yields morphisms

and

of crossed 2-fold extensions. Furthermore, the homomorphisms \(\gamma _{\sharp }, \gamma _{\flat }\), and the obvious unlabeled homomorphisms render the diagram

commutative.
Proof
The left A-module that underlies the twisted group ring \(A^t \varGamma \) is the free A-module having \(\varGamma \) as an A-basis, whence it is manifest that (14.29) yields an action of the group  on that left A-module.
on that left A-module.
Next we show that the  -action on the left A-module that underlies the twisted group ring \(A^t \varGamma \) is compatible with the multiplicative structure of \(A^t \varGamma \). To this end, consider the crossed module
-action on the left A-module that underlies the twisted group ring \(A^t \varGamma \) is compatible with the multiplicative structure of \(A^t \varGamma \). To this end, consider the crossed module  , cf. the middle columns of the commutative diagram (13.3) above. Since
, cf. the middle columns of the commutative diagram (13.3) above. Since  is a morphism of
is a morphism of  -groups, given \(y\in \varGamma \) and
-groups, given \(y\in \varGamma \) and  ,
,

Let  denote the canonical homomorphism. It is now manifest that the action \(\vartheta :\varGamma \rightarrow {\text{ Aut }}(A)\) of \(\varGamma \) on A factors through \(\beta \), that is, \(\vartheta \) coincides with the combined homomorphism
denote the canonical homomorphism. It is now manifest that the action \(\vartheta :\varGamma \rightarrow {\text{ Aut }}(A)\) of \(\varGamma \) on A factors through \(\beta \), that is, \(\vartheta \) coincides with the combined homomorphism

Hence, given  , and \(y\in \varGamma \),
, and \(y\in \varGamma \),
Thus, given  , in view of (14.31) we conclude
, in view of (14.31) we conclude
Consequently (14.29) yields an action of  on the algebra \(A^t \varGamma \).
on the algebra \(A^t \varGamma \).
Finally, to show that the action of  on the algebra \(A^t \varGamma \) preserves the two-sided ideal \(<a-j(a), a\in \mathrm U(A)>\) in \(A^t \varGamma \), let \(a \in \mathrm U(A)\) and
on the algebra \(A^t \varGamma \) preserves the two-sided ideal \(<a-j(a), a\in \mathrm U(A)>\) in \(A^t \varGamma \), let \(a \in \mathrm U(A)\) and  . In view of Proposition 14.13(ii), \(j({}^x a) = {}^\alpha (j(a))\), whence
. In view of Proposition 14.13(ii), \(j({}^x a) = {}^\alpha (j(a))\), whence
\(\square \)
With respect to the crossed pair structure  on \(\tilde{\mathrm {e}}\), the fiber product group
on \(\tilde{\mathrm {e}}\), the fiber product group  is defined. As before, we denote by
is defined. As before, we denote by  the canonical lift, into the fiber product group with respect to the surjection \(\pi _Q:G \rightarrow Q\), of the crossed pair structure
the canonical lift, into the fiber product group with respect to the surjection \(\pi _Q:G \rightarrow Q\), of the crossed pair structure  on \(\tilde{\mathrm {e}}\). Define \(\chi _G :G \rightarrow {\text{ Out }}((A, N,\mathrm {e},\vartheta ),A)\) to be the combined homomorphism
on \(\tilde{\mathrm {e}}\). Define \(\chi _G :G \rightarrow {\text{ Out }}((A, N,\mathrm {e},\vartheta ),A)\) to be the combined homomorphism

Moreover, the composite homomorphism

yields a Q-normal structure  on the central S-algebra \((A, N,\mathrm {e},\vartheta )\). Denote by \(i:\varGamma \rightarrow \mathrm U(A,N, \mathrm {e}, \vartheta )\) the inclusion and by \(\tilde{\gamma }\) the combined homomorphism
on the central S-algebra \((A, N,\mathrm {e},\vartheta )\). Denote by \(i:\varGamma \rightarrow \mathrm U(A,N, \mathrm {e}, \vartheta )\) the inclusion and by \(\tilde{\gamma }\) the combined homomorphism

Proposition 14.15
Write \(C=(A, N,\mathrm {e},\vartheta )\). The homomorphisms  , and \(\tilde{\gamma }\) match in the following sense.
, and \(\tilde{\gamma }\) match in the following sense.
(i) The homomorphisms  and \(\chi _G\) yield a commutative diagram
and \(\chi _G\) yield a commutative diagram

with exact rows.
(ii) The composite homomorphism
coincides with  .
.
(iii) The two homomorphisms i and \(\tilde{\gamma }\) yield a morphism of crossed 2-fold extensions

whence \((i, \tilde{\gamma })\) induces a congruence \((1, i, \cdot , 1) :\mathrm {e}_{\tilde{\psi }} \longrightarrow \mathrm {e}_{((A,N,\mathrm {e} , \vartheta ),\sigma _Q)}\) of crossed 2-fold extensions.
(iv) The homomorphism \(\chi _N:N \rightarrow N^{\mathrm U(C)}(A)/\mathrm U(A)\) turns the embedding of A into \(C=(A, N,\mathrm {e},\vartheta )\) into a strong N-normal Deuring embedding with respect to
Proof
(i) It is obvious that the diagram

is commutative. Combining this diagram with the commutative diagram (14.30), we obtain the right-hand square of (14.34). Since the lower row of that diagram is exact, the homomorphisms \(\chi _G\) and  induce the requisite homomorphism
induce the requisite homomorphism
(ii) Consider the diagram

The right-hand square is commutative in an obvious manner. The left-hand triangle is commutative since, as noted earlier, the composite (14.28) coincides with \(\hat{\psi }\). The upper row yields the homomorphism \(\chi _G :G \rightarrow {\text{ Out }}((A, N,\mathrm {e},\vartheta ),A)\), by the very definition (14.32) of \(\chi _G\).
As noted above, the composite (14.26), viz.  , yields the given G-normal structure
, yields the given G-normal structure  on A. Consequently (14.35) coincides with the structure map
on A. Consequently (14.35) coincides with the structure map  as asserted.
as asserted.
(iii) This is obvious.
(iv) Consider the commutative diagram

By construction, the outer-most diagram coincides with the commutative diagram (12.1), and the left-most column is the composite [14, (4.9)], with N substituted for Q and \({\text{ Aut }}(T|S)\) for \({\text{ Aut }}(S)\). Consequently the composite
is the identity. Since T|S is a Galois extension of commutative rings with Galois group N, by [14, Proposition 5.3(ii)], the algebra A coincides with the centralizer of T in \(C=(A,N,\mathrm {e},\vartheta )\) whence, by [14, Proposition 4.11(iii)], the homomorphism \(\eta _{\flat }\) is injective. Consequently \(\eta _{\flat }\) and \(\chi _N\) are isomorphisms, and \(\chi _N:N \rightarrow N^{\mathrm U(C)}(A)/\mathrm U(A)\) turns the embedding of A into C into a strong N-normal Deuring embedding with respect to \(\mathrm {Id}:N \rightarrow {\text{ Aut }}(T|S)\). \(\square \)
We can now complete the proof of Proposition 14.13: Since the structure homomorphism \(\kappa _G:G \rightarrow {\text{ Out }}(A)\) is a G-normal structure relative to the action
of G on T, by definition, the composite homomorphism

coincides with \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\); since, by Proposition 14.15(ii), the homomorphism (14.35) coincides with  , we conclude that the composite
, we conclude that the composite
coincides with \(\kappa _G\), cf. (14.11).
By Proposition 14.15(i), the diagram (14.34) is commutative, and by Proposition 14.15(iv), the homomorphism \(\chi _N:N \rightarrow N^{\mathrm U(C)}(A)/\mathrm U(A)\) turns the embedding of A into C into a strong N-normal Deuring embedding with respect to
Consequently, cf. (14.32), the homomorphism
turns the embedding of A into \((A, N,\mathrm {e},\vartheta )\) into a strong Q-normal Deuring embedding with respect to the Q-normal structure  on \((A, N,\mathrm {e},\vartheta )\) and the structure extension (14.1).
on \((A, N,\mathrm {e},\vartheta )\) and the structure extension (14.1).
Proposition 14.15(ii) says that the G-normal structure \(G \rightarrow {\text{ Out }}(A)\) on A associated to the strong Q-normal Deuring embedding, cf. (14.12), coincides with the given G-normal structure  on A.
on A.
Propositions 14.13 (i) and 14.15(iii) together entail that the Q-normal S-algebra \(((A,N,\mathrm {e}, \vartheta ), \sigma _Q )\) has Teichmüller class k as asserted since the crossed 2-fold extension \(\mathrm {e}_{\tilde{\psi }}\) represents k.
The proof of Theorem 14.10 is now complete. \(\square \)
Proof
of Complement 14.11. This follows from [14, Proposition 5.4 (xi)]. \(\square \)
Recall that \(B^{\tilde{\psi }}\) denotes the fiber product group  with respect to the crossed pair structure
with respect to the crossed pair structure  on \(\tilde{\mathrm {e}}\), and that, likewise,
on \(\tilde{\mathrm {e}}\), and that, likewise,  denotes the fiber product group
denotes the fiber product group

with respect to the Q-normal structure  on \((A,N,\mathrm {e},\vartheta )\).
on \((A,N,\mathrm {e},\vartheta )\).
Complement 14.16
The canonical homomorphism  induced by the action \(\tilde{\gamma }:B^{\tilde{\psi }}\longrightarrow {\text{ Aut }}^A(A, N,\mathrm {e},\vartheta )\) of \(B^{\tilde{\psi }}\) on the crossed product algebra \((A, N,\mathrm {e},\vartheta )\), cf. (14.33) above, and the surjection \(B^{\tilde{\psi }}\longrightarrow Q\) is an isomorphism.
induced by the action \(\tilde{\gamma }:B^{\tilde{\psi }}\longrightarrow {\text{ Aut }}^A(A, N,\mathrm {e},\vartheta )\) of \(B^{\tilde{\psi }}\) on the crossed product algebra \((A, N,\mathrm {e},\vartheta )\), cf. (14.33) above, and the surjection \(B^{\tilde{\psi }}\longrightarrow Q\) is an isomorphism.
Proof
The homomorphism  makes the diagram
makes the diagram

commutative whence the homomorphism  is an isomorphism. \(\square \)
is an isomorphism. \(\square \)
5 Behavior of the crossed Brauer group under Q-normal Galois extensions
Consider a Q-normal Galois extension T|S of commutative rings, with structure extension \(\mathrm {\mathrm {e}}_{(T|S)} :N\rightarrowtail G \mathop {\twoheadrightarrow }\limits ^{\pi _Q}Q\) and structure homomorphism \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\), cf. Section 12 above, and denote the injection of S into T by \(i:S \rightarrow T\). Then the abelian group \(\mathrm {XB}(T|S;G,Q)\) is defined relative to the associated morphism
in the change of actions category  , cf. (12.3) above.
, cf. (12.3) above.
Theorem 15.1
The sequence
is exact and, furthermore, natural in the data. Moreover, each class in the image of t is also the Teichmüller class of some crossed pair algebra.
Proof
The naturality of the constructions entails that \(\inf \circ \, t = 0\). Moreover, by Theorem 13.5, \(\ker (\inf ) \subset \mathrm {im}(t)\), and each class in the image of t comes from some crossed pair algebra. \(\square \)
Let \({\text{ Pic }}(T|S)\) denote the kernel of the homomorphism \({\text{ Pic }}(S) \rightarrow {\text{ Pic }}(T)\) induced by \(i :S \rightarrow T\). Our next aim is to construct a homomorphism from \(\mathrm H^1(Q, {\text{ Pic }}(T|S))\) to \(\mathrm {XB}(T|S;G,Q)\). To this end, view T as an S-module in the obvious way and let \(A = {\text{ End }}_S(T)\). Now, given an automorphism \(\alpha \) of A so that \(\alpha | S\) is the identity, as above we can turn T into a new A-module \({}^\alpha T\) be means of \(\alpha \), and \(J(\alpha ) = {\text{ Hom }}_A({}^\alpha T, T) \) is a faithful finitely generated projective rank one S-module; since \(A\otimes T\) is a matrix algebra, \(J(\alpha )\) represents a member of \({\text{ Pic }}(T|S)\), and the association \(\alpha \mapsto [J(\alpha )]\) yields a homomorphism \({\text{ Aut }}(A|S) \rightarrow {\text{ Pic }}(T|S)\) which we claim to be surjective. In order to justify this claim, we first observe that the obvious map \(j :T^t N \rightarrow A\), as explained in [14, Section 2], is an isomorphism, since T|S is a Galois extension of commutative rings with Galois group N. Now, given a derivation \(d :N \rightarrow \mathrm U(T)\), define the automorphism \(\alpha _d\) of \(T^t N\) by
Then
is a homomorphism, and \([J(\alpha _d)]\in {\text{ Pic }}(T|S)\) is the image of \([d]\in \mathrm H^1(N, \mathrm U(T))\) under the standard isomorphism \(\mathrm H^1(N,\mathrm U(T)) \rightarrow {\text{ Pic }}(T|S)\) (with N and T substituted for Q and S, respectively, this is, e.g., a consequence of the exactness of [14, (10.1)] at the second term). Hence the homomorphism \({\text{ Aut }}(A|S) \rightarrow {\text{ Pic }}(T|S)\) is surjective as asserted. Consequently the obvious homomorphism from \({\text{ Aut }}(A|S)\) to \({\text{ Aut }}(A,Q)\) fits into a commutative diagram

where the horizontal maps are surjective. Since the G-action on T and that on N induce a canonical section \(\sigma _0 :Q \rightarrow {\text{ Out }}(A,Q)\), the canonical homomorphism from \({\text{ Out }}(A,Q)\) to Q is surjective as well. Consequently the sequence
is exact. Now, given a derivation \(d :Q \rightarrow {\text{ Pic }}(T|S)\), define the homomorphism
by \(\sigma (q) = d(q) \sigma _0 (q)\), as q ranges over Q. Then \((A,\sigma _d)\) is a Q-normal Azumaya S-algebra.
We mention without proof the following.
Theorem 15.2
The association \(d\mapsto ({\text{ End }}_S(T) , \sigma _d)\), as d ranges over derivations from Q to \({\text{ Pic }}(T|S)\), yields a natural isomorphism
of abelian groups in such a way that the resulting sequence
is exact.
6 Relative theory and equivariant Brauer group
Given a morphism \((f,\varphi ) :(S,Q,\kappa ) \rightarrow (T,G,\lambda )\) in the change of actions category  introduced in [14, Subsection 3.7], we denote by \(\mathrm {EB}(T|S; G,Q)\) the kernel of the combined map
introduced in [14, Subsection 3.7], we denote by \(\mathrm {EB}(T|S; G,Q)\) the kernel of the combined map
this kernel \(\mathrm {EB}(T|S; G,Q)\) is the subgroup of \(\mathrm {EB}(S,Q)\) that consists of classes of Q-equivariant S-algebras \((A,\tau )\) so that \((A\otimes T, \tau _{(f,\varphi )})\) is an induced G-normal split algebra and hence, in view of [14, Corollary 7.7], an induced G-equivariant split algebra; see [14, Proposition 4.10(ii)] for the notation \(\tau _{(f,\varphi )}\). Thus, in particular, \(\mathrm {EB}(S|S;Q,Q)\) is the kernel of the canonical homomorphism
whereas \(\mathrm {EB}(S|S;\{e\},Q)\) is the kernel of the forgetful homomorphism from \(\mathrm {EB}(S,Q)\) to \(\mathrm {B}(S)\). It is obvious that the restriction homomorphism
induces a homomorphism
Consider a Q-normal Galois extension T|S of commutative rings, with structure extension \(\mathrm {\mathrm {e}}_{(T|S)} :N\rightarrowtail G \mathop {\twoheadrightarrow }\limits ^{\pi _Q}Q\) and structure homomorphism \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\), cf. Section 12 above, and denote the injection of S into T by \(i:S \rightarrow T\). Then the abelian groups \(\mathrm {EB}(T|S;G,Q)\) and \(\mathrm {XB}(T|S;G,Q)\) are defined relative to the morphism \( (i,\pi _Q):(S,Q,\kappa _Q) \longrightarrow (T,G,\kappa _G) \) in the change of actions category  associated with the data, cf. (12.3) above.
associated with the data, cf. (12.3) above.
Theorem 16.1
Suppose that Q is a finite group. Then the sequence
is exact and natural.
Proof
The statement of the theorem is a consequence of [14, Theorems 6.1, 8.1 (ii), 9.1] and Theorems 14.9 and 15.1.
For if \((A,\sigma )\) represents a member of \(\mathrm {XB}(T|S;G,Q)\) with zero Teichmüller class, by [14, Theorem 6.1], we may assume \((A,\sigma )\) to be equivariant, i.e., \(\sigma = \sigma _\tau \) for some equivariant structure \(\tau \). Now the G-normal algebra  represents zero in \(\mathrm {XB}(T,G)\) and hence is an induced G-normal split algebra, by [14, Theorem 8.1 (ii)]. By [14, Corollary 7.7],
represents zero in \(\mathrm {XB}(T,G)\) and hence is an induced G-normal split algebra, by [14, Theorem 8.1 (ii)]. By [14, Corollary 7.7],  is an induced G-equivariant split algebra. \(\square \)
is an induced G-equivariant split algebra. \(\square \)
Let \(R=S^Q\), let  be a group extension, and denote the restriction to N of the group extension \({\mathrm {e}}_ G\) by
be a group extension, and denote the restriction to N of the group extension \({\mathrm {e}}_ G\) by  . Then the crossed product S-algebra
. Then the crossed product S-algebra  and the crossed product R-algebra
and the crossed product R-algebra

are defined, the former being an Azumaya S-algebra, since T|S is a Galois extension of commutative rings with Galois group N (cf. [14, Proposition 5.4(xi)]), and  contains A as a subalgebra. Consider the resulting group extension
contains A as a subalgebra. Consider the resulting group extension  , of the kind [14, (5.1)], and introduce the notation
, of the kind [14, (5.1)], and introduce the notation  for the obvious injection. Conjugation in \(\varGamma _G\) induces an action
for the obvious injection. Conjugation in \(\varGamma _G\) induces an action  of \(\varGamma _G\) on A such that the pair
of \(\varGamma _G\) on A such that the pair  is a morphism
is a morphism  of crossed modules of the kind [14, (5.2)], and this morphism, in turn, induces a Q-normal structure
of crossed modules of the kind [14, (5.2)], and this morphism, in turn, induces a Q-normal structure  on A; thus the crossed product R-algebra
on A; thus the crossed product R-algebra

can now be written as the crossed product R-algebra  relative to the group extension \(\mathrm {e}_Q\) and the morphism
relative to the group extension \(\mathrm {e}_Q\) and the morphism  of crossed modules, cf. [14, Section 5]. In particular, the left A-module
of crossed modules, cf. [14, Section 5]. In particular, the left A-module  that underlies the algebra
that underlies the algebra

is free with basis in one-one correspondence with the elements of Q, and the Q-equivariant structure  given as [14, (5.5)] is defined. When the group Q is finite, the algebra
given as [14, (5.5)] is defined. When the group Q is finite, the algebra  is an Azumaya S-algebra.
is an Azumaya S-algebra.
Proposition 16.2
Suppose that the group Q is finite. Then the assignment to a group extension \(\mathrm {e}_G\) of G by \(\mathrm U(T)\) of the Q-equivariant algebra  yields a homomorphism
yields a homomorphism
of abelian groups that is natural on the change of actions category  . In the special case where \(T=S\) and N is the trivial group, the homomorphism (16.2) comes essentially down to [14, (9.2)], viz.
. In the special case where \(T=S\) and N is the trivial group, the homomorphism (16.2) comes essentially down to [14, (9.2)], viz.
\(\square \)
7 The eight term exact sequence
Given a morphism \((f,\varphi ) :(S,Q, \kappa ) \rightarrow (T,G,\lambda )\) in the change of actions category  introduced in [14, Subsection 3.7], the group Q being finite, the corresponding relative version of the exact sequence [14, (10.1)] takes the following form:
introduced in [14, Subsection 3.7], the group Q being finite, the corresponding relative version of the exact sequence [14, (10.1)] takes the following form:

Remark 17.1
In the special case where \(T = S\) and G is the trivial group, in view of the isomorphism [14, (8.3)] from \(\mathrm {XB}(S|S;\{e\},Q)\) onto \(\mathrm H^1(Q,{\text{ Pic }}(S))\), the sequence (17.1) has the form of the C(hase-)R(osenberg-)A(uslander-)B(rumer) sequence [3, Theorem 7.6 p. 62], [1]. Other versions of the CRAB-sequence were obtained by Childs [4, Theorem 2.2], Fröhlich and Wall [7, Theorem 1], [6], [9, Theorem 4.2] (upper and middle long sequence), Hattori [10], Kanzaki [16], Ulbrich [18], Yokogawa [20], and Villamayor-Zelinski [19].
Consider a Q-normal Galois extension T|S of commutative rings, with structure extension \(\mathrm {\mathrm {e}}_{(T|S)} :N\rightarrowtail G \mathop {\twoheadrightarrow }\limits ^{\pi _Q}Q\) and structure homomorphism \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\), cf. Section 12 above, and denote the injection of S into T by \(i:S \rightarrow T\). Then the abelian groups \(\mathrm {EB}(T|S;G,Q)\) and \(\mathrm {XB}(T|S;G,Q)\) are defined relative to the morphism \( (i,\pi _Q):(S,Q,\kappa _Q) \longrightarrow (T,G,\kappa _G) \) in the change of actions category  associated with the data, cf. (12.3) above.
associated with the data, cf. (12.3) above.
Theorem 17.2
The group Q being finite, the extension

of the exact sequence [14, (3.15)] is defined and yields an eight term exact sequence that is natural in terms of the data. If, furthermore, S|R and T|R are Galois extensions of commutative rings over \(R=S^Q=T^G\), with Galois groups Q and G, respectively, then, with \({\text{ Pic }}(S|R), {\text{ Pic }}(R)\) and \(\mathrm B(T|R)\) substituted for, respectively \(\mathrm H^1(Q,\mathrm U(S)), \mathrm {EPic} (S,Q)\) and \(\mathrm {EB}(S,Q)\), where \(R = S^Q\), the homomorphisms cpr and res being modified accordingly, the sequence is exact as well.
Proof
This is an immediate consequence of Theorem 16.1 and [14, Theorem 10.1]. \(\square \)
Remark 17.3
In terms of the notation \(B_0(R;\varGamma )\) for the group that corresponds to our \(\mathrm {EB}(S|S;Q,Q)\) (where our notation Q and S corresponds to \(\varGamma \) and R, respectively), a homomorphism of the kind (16.3) above is given in [9, Theorem 4.2]. After the statement of Theorem 4.2, the authors of [9] remark that there is no direct construction for the map from \(\mathrm H^2(\varGamma ; \mathrm U(R))\) to \(B_0(R;\varGamma )\). Our construction of (16.3) is direct, however.
Remark 17.4
In the special case where T|S|R are ordinary Galois extensions of fields, the exact sequence boils down to the classical low degree five term exact sequence
see [11, p. 130].
8 Relationship with the eight term exact sequence in the cohomology of a group extension
Let T|S be a Q-normal Galois extension of commutative rings, with structure extension \(\mathrm {\mathrm {e}}_{(T|S)} :N\rightarrowtail G \mathop {\twoheadrightarrow }\limits ^{\pi _Q}Q\) and structure homomorphism \(\kappa _G:G \rightarrow {\text{ Aut }}^S(T)\), cf. Section 12 above; in particular, N is a finite group. Since \(\mathrm U(T)^N\) coincides with \(\mathrm U(S)\), the eight term exact sequence in [13] associated with the group extension \(\mathrm {e}_{(T|S)}\) and the G-module \(\mathrm U(T)\), reproduced as (13.4) above, has the following form:
8.1 Relationship between the two long exact sequences
Consider the morphism \((i,\pi _Q ):(S,Q,\kappa _Q) \longrightarrow (T,G,\kappa _G)\) associated to the given Q-normal Galois extension, cf. 12.3, in the change of actions category  introduced in [14, Subsection 3.7]. The abelian groups \(\mathrm {EB}(T|S;G,Q)\) and \(\mathrm {XB}(T|S;G,Q)\) are now defined relative to this morphism.
introduced in [14, Subsection 3.7]. The abelian groups \(\mathrm {EB}(T|S;G,Q)\) and \(\mathrm {XB}(T|S;G,Q)\) are now defined relative to this morphism.
The assignment to a crossed pair \( \left( \mathrm {e} :\mathrm U(T)\rightarrowtail \varGamma \twoheadrightarrow N,\ \psi :Q \rightarrow {\text{ Out }}_G(\mathrm {e})\right) \) with respect to \({\mathrm {e}}_ {(T|S)}\) and \(\mathrm U(T)\) of its associated crossed pair algebra \((A_{\mathrm {e}},\sigma _\psi )\), cf. Section 13 above, yields a homomorphism
Let \(\mathrm {EPic}(T|S,Q)\) denote the kernel of the induced homomorphisms

and \({\text{ Pic }}(T|S)\) that of the induced homomorphism \(i_*:{\text{ Pic }}(S) \rightarrow {\text{ Pic }}(T)\). With T and G substituted for S and Q, respectively, the isomorphism [14, (3.17)] takes the form

and Galois descent, cf. [14, Subsection 2.2 (ii)], yields an isomorphism
whence (18.3) induces a homomorphism
of abelian groups. The homomorphism (18.4) admits, of course, a straightforward direct description. Likewise, with T and N substituted for Q and S, respectively, the isomorphism [14, (3.17)] takes the form

and Galois descent, cf. [14, Subsection 2.2 (ii)], yields an isomorphism
whence (18.5) induces an isomorphism
of abelian groups, necessarily compatible with the Q-module structures; the isomorphism (18.6) is entirely classical. Below we do not distinguish in notation between (18.4) and its composite
with the canonical injection of \(\mathrm {EPic}(T|S,Q)\) into \(\mathrm {EPic}(T,Q)\), nor between (18.6) and its composite \(\mathrm H^1(N,\mathrm U(T)) \rightarrow {\text{ Pic }}(S)\) with the canonical injection \({\text{ Pic }}(T|S) \rightarrow {\text{ Pic }}(S)\). Direct inspection establishes the following.
Theorem 18.1
The group Q being finite, the homomorphisms (18.4), (18.6), (16.2), and (18.2) of abelian groups are natural on the category  and induce a morphism of exact sequences from (18.1) to (17.2). \(\square \)
and induce a morphism of exact sequences from (18.1) to (17.2). \(\square \)
Remark 18.2
Consider the classical case where R, S, and T are fields. Now the group \(\mathrm {Xpext} (G,N;\mathrm U(T))\) comes down to \(\mathrm H^2(N,\mathrm U(T))^Q\) and, likewise, the group \(\mathrm {XB}(T|S;G,Q)\) to \(\mathrm B(T|S)^Q\), and (18.2) boils down to the classical isomorphism
Furthermore, the groups \(\mathrm H^1(N,\mathrm U(T)), \mathrm H^1(G,\mathrm U(T)), \mathrm {EPic}(T|S,Q)\), and \(\mathrm {Pic}(T|S)\) are zero, and (16.2) is an isomorphism. Thus the morphism (18.1) \(\rightarrow \) (17.2) of exact sequences in Theorem 18.1 above is then an isomorphism of exact sequences.
8.2 An application
Let T|S be a Galois extension of commutative rings, with Galois group N, suppose that T carries a Q-action that extends the given Q-action on S, and define the group \(\mathrm {EB}(T|S,Q)\) to be the kernel of the induced homomorphism
Relative to the induced Q-action on N, the semi-direct product group \(N \rtimes Q\) is defined, and T|S is a Q-normal Galois extension of rings, having as structure extension the split extension \(\mathrm {\mathrm {e}}_{(T|S)} :N\rightarrowtail N \rtimes Q \twoheadrightarrow Q\). Consider the commutative diagram

of abelian groups with exact rows and columns, the abelian group \(\widetilde{\mathrm {EB}(T|S,Q)}\), necessarily (isomorphic to) a subgroup of \(\mathrm {EB}(T|S,Q)\), being defined by the requirement that the upper row be exact.
The group N being finite, suppose now that Q is a finite group as well. The corresponding homomorphism (16.2), viz.
and the homomorphism (16.3), with T substituted for S, viz.
yield the commutative diagram

with exact rows and hence a homomorphism
of abelian groups. Suppose, furthermore, that S and T are fields. Then the homomorphism
in the lower row of the diagram (18.7) comes down to the obvious injection
whence the group \(\mathrm {XB}(T;Q,N \rtimes Q)\) is now trivial and the inclusion
is the identity. Moreover, the right-hand and the middle vertical arrow in (18.8) are isomorphisms whence the induced homomorphism \(\mathrm {ker}(\mathrm {res}) \rightarrow \mathrm {EB}(T|S,Q)\) is an isomorphism. This observation recovers and casts new light on the main result of [2], obtained there via relative group cohomology. Our argument is elementary and does not invoke relative group cohomology. Indeed, the main point of our reasoning is the identification of the group cohomology group \(\mathrm H^2(N \rtimes Q,\mathrm U(T))\) with the group \(\mathrm {EB}(T|S;N \rtimes Q,Q)\); under the present circumstances, this group is the subgroup of the Q-equivariant Brauer group \(\mathrm {EB}(S,Q)\) of S that consists of classes of Q-equivariant central simple S-algebras A such that \(A\otimes T\) is a matrix algebra over T. Likewise, the group \(\mathrm {EB}(T|T;Q,Q)\) is the subgroup of the Q-equivariant Brauer group \(\mathrm {EB}(T,Q)\) of T that consists of classes of Q-equivariant matrix algebras over T. The group \(\mathrm {EB}(T|S,Q)\) then appears as the kernel of the canonical homomorphism \(\mathrm {EB}(T|S;N \rtimes Q,Q) \rightarrow \mathrm {EB}(T|T;Q,Q)\) and, in view of the identifications of \(\mathrm H^2(N \rtimes Q,\mathrm U(T))\) with \(\mathrm {EB}(T|S;N \rtimes Q,Q)\) and of \(\mathrm H^2(Q,\mathrm U(T))\) with \(\mathrm {EB}(T|T;Q,Q)\), the identification of \(\mathrm {ker}(\mathrm {res}:\mathrm H^2(N \rtimes Q,\mathrm U(T)) \rightarrow \mathrm H^2(Q,\mathrm U(T)))\) with \(\mathrm {EB}(T|S,Q)\) is immediate. In particular, when the group Q is trivial, that result comes down to the classical Brauer–Hasse–Noether isomorphism between the corresponding second group cohomology group and the corresponding subgroup of the ordinary Brauer group.
8.3 A variant of the relative theory
In the situation of the relative versions (17.1) and (17.2) of the long exact sequence [14, (10.1)], in general, there is no obvious reason for a homomorphism \(\omega \) from \(\mathrm H^0(Q,\mathrm B(T|S))\) to \(\mathrm H^2(Q,{\text{ Pic }}(T|S))\) to exist that would complete

to a commutative square and hence would complete the exact sequence (15.1) to a corresponding relative version of an exact sequence of the kind [14, (3.14)]. We now show that a variant of the relative theory includes such a homomorphism.
The object \((S,Q,\kappa _Q)\) of the category  being given, let \((T,G,\kappa _G)\) be another object of
being given, let \((T,G,\kappa _G)\) be another object of  , and let \((f,\varphi ):(S,Q,\kappa _Q) \rightarrow (T,G,\kappa _G)\) be a morphism in
, and let \((f,\varphi ):(S,Q,\kappa _Q) \rightarrow (T,G,\kappa _G)\) be a morphism in  having \(\varphi :G \rightarrow Q\) surjective, cf. [14, Subsection 3.7].
having \(\varphi :G \rightarrow Q\) surjective, cf. [14, Subsection 3.7].
8.3.1 The standard approach
We say that two Q-normal Azumaya S-algebras \((A_1,\sigma _1)\) and \((A_2,\sigma _2)\) such that \({T \otimes A_1}\) and \(T \otimes A_2\) are matrix algebras over T are relatively Brauer equivalent if there are faithful finitely generated projective S-modules modules \(M_1\) and \(M_2\) having the property that \(T \otimes M_1\) and \(T \otimes M_2\) are free as T-modules, together with induced Q-normal structures
such that \((A_1 \otimes B_1, \sigma _1 \otimes \rho _1 )\) and \((A_2 \otimes B_2, \sigma _2 \otimes \rho _2)\) are isomorphic Q-normal S-algebras. Just as for \(\mathrm {XB}(S,Q)\), under the operations of tensor product and that of taking opposite algebras, the equivalence classes constitute an abelian group, the identity element being represented by \((S,\kappa _Q)\). We refer to this group as the T-relative
Q-crossed Brauer group of
S
with respect to the morphism
\((f,\varphi )\) in  , denote this group by \(\mathrm {XB}_{\mathrm {fr}}(T|S;G,Q)\), and we refer to the construction just given as the standard construction. The T-relative
Q-equivariant Brauer group
\(\mathrm {EB}_{\mathrm {fr}}(T|S;G,Q)\)
with respect to the morphism
\((f,\varphi )\) in
, denote this group by \(\mathrm {XB}_{\mathrm {fr}}(T|S;G,Q)\), and we refer to the construction just given as the standard construction. The T-relative
Q-equivariant Brauer group
\(\mathrm {EB}_{\mathrm {fr}}(T|S;G,Q)\)
with respect to the morphism
\((f,\varphi )\) in  arises in the same way as the relative Q-crossed Brauer group, save that, in the definition, ‘equivariant’ is substituted for ‘crossed’, and we likewise say that this construction is the standard construction. In particular, when we forget the actions, that is, we take the groups G and Q to be trivial, this construction yields an abelian group \(\mathrm B_{\mathrm {fr}}(T|S)\) which we refer to as the T-relative Brauer group of
S, obtained by the standard construction.
arises in the same way as the relative Q-crossed Brauer group, save that, in the definition, ‘equivariant’ is substituted for ‘crossed’, and we likewise say that this construction is the standard construction. In particular, when we forget the actions, that is, we take the groups G and Q to be trivial, this construction yields an abelian group \(\mathrm B_{\mathrm {fr}}(T|S)\) which we refer to as the T-relative Brauer group of
S, obtained by the standard construction.
The group \(\mathrm B_{\mathrm {fr}}(T|S)\) acquires a Q-module structure. Indeed, let \(R=S^Q\). Given an S-module M and \(x\in Q\), let \({}^xM\) denote the S-module whose underlying R-module is just M, and whose S-module structure is given by
Consider a faithful finitely generated projective S-module M such that \(T \otimes M\) is a free T-module, let \(x \in Q\), and pick a pre-image \(y \in G\) of \(x\in Q\). Then the association
yields an isomorphism of T-modules, and since \(T\otimes M\) is a free T-module, so is \({}^y(T \otimes M)\); further,
is a matrix algebra over T. Likewise, given an Azumaya S-algebra A such that \(T\otimes A\) is a matrix algebra over T and \(x\in Q\), to show that \(T \otimes {}^xA\) is a matrix algebra over T, pick a pre-image \(y \in G\) of \(x \in Q\) and note that the corresponding association (18.9) yields an isomorphism of T-algebras. Since \(T \otimes A\) is a matrix algebra over T, so is \({}^y (T \otimes A)\).
By construction, the canonical homomorphism
is a morphism of Q-modules but in general there is no reason for this homomorphism to be injective nor to be surjective. The assignment to a Q-equivariant Azumaya S-algebra representing a member of \(\mathrm {EB}_{\mathrm {fr}}(T|S;G,Q)\) of the associated Q-normal Azumaya S-algebra yields a homomorphism \(\mathrm {res}_{\mathrm {fr}}:\mathrm {EB}_{\mathrm {fr}}(T|S;G,Q)\rightarrow \mathrm {XB}_{\mathrm {fr}}(T|S;G,Q)\) of abelian groups, the assignment to a Q-normal Azumaya S-algebra \((A, \sigma )\) representing a member of \(\mathrm {XB}_{\mathrm {fr}}(T|S;G,Q)\) of its Teichmüller complex \(\mathrm {e}_{(A, \sigma )}\) yields a homomorphism \(t_{\mathrm {fr}}:\mathrm {XB}_{\mathrm {fr}}(T|S;G,Q) \longrightarrow \mathrm H^3(Q,\mathrm U(S)) \) of abelian groups and, when the group Q is finite, the construction of the homomorphism
cf. (16.3) above, lifts to a homomorphism
Remark 18.3
The abelian groups \(\mathrm {EB}(T|S;G,Q)\) and \(\mathrm {XB}(T|S;G,Q)\) being defined relative to the given morphism \((f,\varphi )\) in  , the obvious maps yield homomorphisms
, the obvious maps yield homomorphisms
of abelian groups that make the diagram

commutative and, when the group Q is finite, the homomorphisms
extend the diagram to a larger commutative diagram having four terms in each row. However, there is no reason for the homomorphisms (18.10) or (18.11) to be injective nor to be surjective, nor is there a reason, when Q is a finite group, for
to be injective or surjective. In the classical situation where R, S, T are fields etc., these homomorphisms are, of course, isomorphisms.
Let \(\mathrm {Pic}(T|S)\) denote the kernel of the homomorphism \(\mathrm {Pic}(S) \rightarrow \mathrm {Pic}(T)\) induced by the ring homomorphism \(f:S \rightarrow T\), necessarily a morphism of G-modules when G acts on S through \(\varphi :G \rightarrow Q\) whence, in particular, the abelian subgroup \(\mathrm {Pic}(T|S)^Q\) of Q-invariants is defined, and let \(\mathrm {EPic}(T|S,Q)\) denote the kernel of the homomorphism \(\mathrm {EPic}(S,Q) \rightarrow \mathrm {EPic}(T,G)\) induced by the morphism \((f,\varphi )\) in  . It is immediate that the low degree exact sequence [14, (3.14)] restricts to the exact sequence
. It is immediate that the low degree exact sequence [14, (3.14)] restricts to the exact sequence

of abelian groups. In the Appendix (cf. Subsection 19.2 below), we shall show that, with a suitably defined Picard category  substituted for
substituted for  , the sequence (18.12) is as well a special case of the exact sequence [14, (3.10)].
, the sequence (18.12) is as well a special case of the exact sequence [14, (3.10)].
Theorem 18.4
Suppose that the group Q is finite. Then the extension

of the exact sequence (18.12) is defined and yields a seven term exact sequence that is natural in terms of the data.
Proof
Essentially the same reasoning as that for [14, Theorem 10.1] establishes this theorem as well. We explain only the requisite salient modifications.
Exactness at \(\mathrm {XB}_{\mathrm {fr}}(T|S;G,Q)\): This follows again from [14, Theorem 6.1] or [14, Theorem 9.1].
Exactness at \(\mathrm H^2(Q,\mathrm U(S))\): Let J represent a class in \(({\text{ Pic }}(T|S))^Q\), and proceed as in the proof of the exactness at \(\mathrm H^2(Q,\mathrm U(S))\) in [14, Theorem 10.1]. Now \(T \otimes J\) is free as a T-module and, with reference to the associated group extension \(\mathrm {e}_J\), cf. [14, (10.2)], by construction, \(M_{\mathrm {e}_J}\) is free as an S-module whence \(T \otimes M_{\mathrm {e}_J}\) is free as a T-module. Hence
is free as a T-module. Consequently \(({\text{ End }}_S(M_{\mathrm {e}_J}),\tau _{\mathrm {e}_J})\) represents zero in the group \(\mathrm {EB}_{\mathrm {fr}}(T|S;G,Q)\).
Conversely, let \(\mathrm {e} :\mathrm U(S) \rightarrowtail \varGamma \twoheadrightarrow Q\) be a group extension, and proceed as in the proof of the exactness at \(\mathrm H^2(Q,\mathrm U(S))\) in [14, Theorem 10.1]. Thus suppose that \(({\text{ End }}_S(M_{\mathrm {e}}), \tau _{\mathrm {e}})\) represents zero in \(\mathrm {EB}_{\mathrm {fr}}(T|S;G,Q)\). Then there are \(S^tQ\)-modules \(M_1\) and \(M_2\) whose underlying S-modules are faithful and finitely generated projective such that the following hold, where we denote by \(\tau _1:Q \rightarrow {\text{ Aut }}({\text{ End }}_S(M_1))\) and \({\tau _2:Q \rightarrow {\text{ Aut }}({\text{ End }}_S(M_2))}\) the associated trivially induced Q-equivariant structures: The algebras \( ({\text{ End }}_S(M_{\mathrm {e}}),\tau _{\mathrm {e}})\otimes ({\text{ End }}_S(M_1),\tau _1) \) and \(({\text{ End }}_S(M_2),\tau _2) \) are isomorphic as Q-equivariant S-algebras and, furthermore, the T-modules \(T\otimes M_1\) and \(T\otimes M_2\) are free as T-modules. Consequently the T-module \(T \otimes S\) arising from the finitely generated and projective rank one S-module \(J = {\text{ Hom }}_{{\text{ End }}_S(M_{\mathrm {e}}\otimes M_1)}(M_{\mathrm {e}}\otimes M_1,M_2)\) is free of rank one whence \([J]\in {\text{ Pic }}(T|S)\). The group extension \(\mathrm {e}_J\), cf. [14, (10.2)], is now defined relative to J, whence \([J]\in ({\text{ Pic }}(T|S))^Q\), and the \(\varGamma \)-action on J induces a homomorphism \(\varGamma \rightarrow {\text{ Aut }}(J,Q)\) which yields a congruence \((1,\cdot ,1) :{\mathrm {e}} \rightarrow \mathrm {e}_J \) of group extensions, and this congruence entails that  .
.
Exactness at \(\mathrm {EB}_{\mathrm {fr}}(T|S;G,Q)\): The argument in the proof of [14, Theorem 10.1] which shows that the composite \({\text{ res }}\circ \,\mathrm {cpr}\) is zero shows as well that the composite \({\text{ res }}_{\mathrm {fr}} \circ \,\mathrm {cpr}_{\mathrm {fr}}\) is zero.
To show that \(\ker ({\text{ res }}_{\mathrm {fr}}) \subseteq {\text{ im }}(\mathrm {cpr}_{\mathrm {fr}})\), let \((A,\tau )\) be a Q-equivariant Azumaya S-algebra representing a member of \(\mathrm {EB}_{\mathrm {fr}}(T|S;G,Q)\), and suppose that the class of its associated Q-normal algebra \((A,\sigma _\tau )\) goes to zero in \(\mathrm {XB}_{\mathrm {fr}}(T|S;G,Q)\). As in the proof of the exactness at \(\mathrm {EB}(S,Q)\) in [14, Theorem 10.1], there are two induced Q-equivariant split algebras \(({\text{ End }}_S(M_1),\tau _1)\) and \(({\text{ End }}_S(M_2),\tau _2)\) over faithful finitely generated projective S-modules \(M_1\) and \(M_2\), respectively, such that \((A,\tau ) \otimes ({\text{ End }}_S(M_1),\tau _1)\) and \(({\text{ End }}_S(M_2),\tau _2)\) are isomorphic as Q-equivariant central S-algebras but now we may furthermore take \(M_1\) and \(M_2\) to have the property that the T-modules \(T \otimes M_1\) and \(T \otimes M_2\) are free of finite rank. Essentially the same reasoning as that in the proof of the exactness at \(\mathrm {EB}(S,Q)\) in [14, Theorem 10.1] yields a group extension
such that
\(\square \)
Consider a Q-normal Galois extension T|S of commutative rings, with structure extension \(\mathrm {\mathrm {e}}_{(T|S)} :N\rightarrowtail G \mathop {\twoheadrightarrow }\limits ^{\pi _Q}Q\) and structure homomorphism
cf. Section 12 above, and take the morphism \((f,\varphi )\) to be the morphism
in  associated to that Q-normal Galois extension, cf. (12.3).
associated to that Q-normal Galois extension, cf. (12.3).
Theorem 18.5
Suppose that the group Q is finite. Then the extension

of the exact sequence (18.12) is defined and yields an eight term exact sequence that is natural in terms of the data.
Proof
Essentially the same reasoning as that for Theorem 17.2 establishes this theorem as well. We leave the details to the reader. \(\square \)
The homomorphism (18.2) now lifts to a homomorphism
such that (18.2) may be written as the composite
and, when Q and hence G is a finite group, the homomorphism (16.2) lifts to a homomorphism
such that (16.2) may be written as the composite
Theorem 18.1, adjusted to the present circumstances, takes the following form which, again, we spell out without proof.
Theorem 18.6
The group Q being finite, the maps (18.15), (18.4), (18.6), and (18.17) are natural homomorphisms of abelian groups and induce a morphism
of exact sequences.
8.3.2 The Morita equivalence approach
We define the Q-graded relative Brauer precategory associated with the morphism
\((f,\varphi )\) in  to be the precategory
to be the precategory  that has as its objects the Azumaya S-algebras A such that \(T \otimes A\) is a matrix algebra over T, a morphism
that has as its objects the Azumaya S-algebras A such that \(T \otimes A\) is a matrix algebra over T, a morphism
in  of grade
\(x\in Q\) between two Azumaya algebras A and B in
of grade
\(x\in Q\) between two Azumaya algebras A and B in  , necessarily an isomorphism in
, necessarily an isomorphism in  , being a morphism in
, being a morphism in  , that is, a pair ([M], x) where [M] is an isomorphism class of an invertible (B, A)-bimodule M of grade \(x\in Q\), such that, furthermore, \(T \otimes M\) is free as a T-module. There is no reason for composition in the ambient category
, that is, a pair ([M], x) where [M] is an isomorphism class of an invertible (B, A)-bimodule M of grade \(x\in Q\), such that, furthermore, \(T \otimes M\) is free as a T-module. There is no reason for composition in the ambient category  to induce an operation of composition in
to induce an operation of composition in  since, given three Azumaya algebras A, B, C in
since, given three Azumaya algebras A, B, C in  and morphisms \(([{}_BM_A],x):A \rightarrow B\) and \(([{}_AM_C],x):C\rightarrow A\) of grade \(x \in Q\) in
and morphisms \(([{}_BM_A],x):A \rightarrow B\) and \(([{}_AM_C],x):C\rightarrow A\) of grade \(x \in Q\) in  , while the composite \(([{}_BM_A\otimes _A {}_AM_C],x):C\rightarrow B\) of grade \(x\in Q\) in
, while the composite \(([{}_BM_A\otimes _A {}_AM_C],x):C\rightarrow B\) of grade \(x\in Q\) in  is defined, there is no reason for the \((T \otimes B,T\otimes C)\)-bimodule
is defined, there is no reason for the \((T \otimes B,T\otimes C)\)-bimodule
to be free as a T-module. To overcome this difficulty, we take the Q-graded relative Brauer category associated with the morphism
\((f,\varphi )\) in  to be the subcategory
to be the subcategory  of
of  generated by
generated by  . Thus a morphism in
. Thus a morphism in  of grade \(x \in Q\) between two objects A and B of
of grade \(x \in Q\) between two objects A and B of  is a morphism \(([{}_BM_A],x):A \rightarrow B\) in
is a morphism \(([{}_BM_A],x):A \rightarrow B\) in  of grade \(x \in Q\) such that there are objects \(A_1\),..., \(A_n\) of
of grade \(x \in Q\) such that there are objects \(A_1\),..., \(A_n\) of  and morphisms \(([{}_{A_{j+1}}M_{A_j}],x):A_j \rightarrow A_{j+1}\) in
and morphisms \(([{}_{A_{j+1}}M_{A_j}],x):A_j \rightarrow A_{j+1}\) in  such that, when we write A as \(A_0\) and B as \(A_n\),
such that, when we write A as \(A_0\) and B as \(A_n\),
We then define composition, monoidal structure, the operation of inverse, and the unit object as in  . The resulting category
. The resulting category  is a group-like stably Q-graded symmetric monoidal category. Hence the category
is a group-like stably Q-graded symmetric monoidal category. Hence the category  is group-like and thence
is group-like and thence  is an abelian group. When the groups G and Q are trivial, that is, we consider merely the homomorphism \(f :S \rightarrow T\) of commutative rings, the same construction yields a precategory
is an abelian group. When the groups G and Q are trivial, that is, we consider merely the homomorphism \(f :S \rightarrow T\) of commutative rings, the same construction yields a precategory  and, accordingly, the corresponding group-like symmetric monoidal category
and, accordingly, the corresponding group-like symmetric monoidal category  which we refer to as the relative Brauer category associated with the homomorphism
\(f:S \rightarrow T\) of commutative rings. The category
which we refer to as the relative Brauer category associated with the homomorphism
\(f:S \rightarrow T\) of commutative rings. The category  has
has  as its unit group, is group-like, and
as its unit group, is group-like, and  is therefore an abelian group. The ring homomorphism \(f:S \rightarrow T\) being a constituent of the morphism \((f,\varphi )\) in
is therefore an abelian group. The ring homomorphism \(f:S \rightarrow T\) being a constituent of the morphism \((f,\varphi )\) in  having \(\varphi \) surjective, the category
having \(\varphi \) surjective, the category  has
has  and
and

as its unit group.
Given two objects A and B of  we define, with respect to the morphism
\((f,\varphi )\)
in
we define, with respect to the morphism
\((f,\varphi )\)
in
 , a relative Morita equivalence of grade
\(x \in Q\)
between
A
and
B to be a string of isomorphisms in
, a relative Morita equivalence of grade
\(x \in Q\)
between
A
and
B to be a string of isomorphisms in  of the kind (18.18) above. It is immediate that, as in the classical situation, given two objects \(A_1\) and \(A_2\) of
of the kind (18.18) above. It is immediate that, as in the classical situation, given two objects \(A_1\) and \(A_2\) of  , a relative Brauer equivalence
, a relative Brauer equivalence
between \(A_1\) and \(A_2\) induces a string
of isomorphisms in  and hence a relative Morita equivalence between \(A_1\) and \(A_2\) (of grade \(e\in Q\)) whence the obvious association induces a homomorphism
and hence a relative Morita equivalence between \(A_1\) and \(A_2\) (of grade \(e\in Q\)) whence the obvious association induces a homomorphism

of abelian groups, necessarily surjective. Moreover, since  is stably graded,
is stably graded,  acquires a Q-module structure, and the homomorphism (18.19) is a morphism of Q-modules.
acquires a Q-module structure, and the homomorphism (18.19) is a morphism of Q-modules.
Proposition 18.7
The homomorphism (18.19) is an isomorphism, that is, relative Brauer equivalence is equivalent to relative Morita equivalence.
Proof
The classical argument, suitably rephrased, carries over: Let A and B be two Azumaya S-algebras A in  and consider a morphism
\([M]:A \rightarrow B\) in
and consider a morphism
\([M]:A \rightarrow B\) in  . We must show that A and B are relatively Brauer equivalent. Now \(B^{\mathrm {op}}\cong {}_A{\text{ End }}(M)\) (the algebra of left A-endomorphisms of M), and
. We must show that A and B are relatively Brauer equivalent. Now \(B^{\mathrm {op}}\cong {}_A{\text{ End }}(M)\) (the algebra of left A-endomorphisms of M), and
whence
Since \(T \otimes M\) and \(T\otimes B\) are free as T-modules, A and B are relatively Brauer equivalent. \(\square \)
With N, T, S substituted for, respectively, Q, S, R, the standard homomorphism [14, (5.6)] from \(\mathrm H^2(N,U)\) to \(\mathrm B(T|S)\), necessarily a morphism of Q-modules, lifts to a morphism
of Q-modules. By construction, the assignment to an automorphism in  of an Azumaya algebra A in
of an Azumaya algebra A in  of its grade in Q yields a homomorphism
of its grade in Q yields a homomorphism

which is surjective if and only if the Brauer class \([A]\in \mathrm B_{\mathrm {fr}}(T|S)\) of A in  is fixed under Q, and the group
is fixed under Q, and the group  associated to an Azumaya S-algebra A in
associated to an Azumaya S-algebra A in  whose Brauer class \([A]\in \mathrm B_{\mathrm {fr}}(T|S)\) is fixed under Q fits into a group extension of the kind [14, (3.6)], viz.
whose Brauer class \([A]\in \mathrm B_{\mathrm {fr}}(T|S)\) is fixed under Q fits into a group extension of the kind [14, (3.6)], viz.

with abelian kernel in such a way that the assignment to A of  yields a homomorphism
yields a homomorphism

The sequence [14, (3.10)] now takes the form

and is an exact sequence of abelian groups since the category  is group-like. Furthermore, the association that defines the homomorphism [14, (8.4)] yields an injective homomorphism
is group-like. Furthermore, the association that defines the homomorphism [14, (8.4)] yields an injective homomorphism

in such a way that the diagram

is commutative, the unlabeled vertical arrows being the obvious maps, and the argument for [14, Theorem 8.10 (iii)], adjusted to the present situation, shows that if Q (and hence G) is a finite group, the homomorphism \(\theta _{\mathrm {fr}}\) is surjective and hence an isomorphism of abelian groups. Thus when the group Q is finite, the exact sequence (18.23) is available with \(\mathrm {XB}_{\mathrm {fr}}(T|S;G,Q)\) substituted for  .
.
Consider a Q-normal Galois extension T|S of commutative rings, with structure extension \(\mathrm {\mathrm {e}}_{(T|S)} :N\rightarrowtail G \mathop {\twoheadrightarrow }\limits ^{\pi _Q}Q\) and structure homomorphism
cf. Section 12 above, and take the morphism \((f,\varphi )\) to be the morphism
in  associated with that Q-normal Galois extension, cf. 12.3. Comparison of the exact sequences [14, (3.14)] and (18.23) with [13, (1.9)] yields the following result, which we spell out without proof.
associated with that Q-normal Galois extension, cf. 12.3. Comparison of the exact sequences [14, (3.14)] and (18.23) with [13, (1.9)] yields the following result, which we spell out without proof.
Theorem 18.8
Write \(U=\mathrm U(T)\). The various groups and homomorphisms fit into a commutative diagram

with exact rows; here the top row is the exact sequence [13, (1.9)], the middle row the sequence (18.23), the bottom row the exact sequence [14, (3.14)], the unlabeled arrow from \(\mathrm H^0(Q,\mathrm H^2(N,U))\) to \(\mathrm H^0(Q,\mathrm B_{\mathrm {fr}}(T|S))\) is induced by the homomorphism (18.20), and the other unlabeled arrows are either the obvious ones or have been introduced before. If, furthermore, the group Q is a finite group, the above diagram is available with \(\mathrm {XB}_{\mathrm {fr}}(T|S;G,Q)\) substituted for  and \(\mathrm {XB}(S,Q)\) for
and \(\mathrm {XB}(S,Q)\) for  .
.
Remark 18.9
The exact sequences (18.14) and (18.23) are presumably related with an equivariant Amitsur cohomology spectral sequence of the kind given in [4, Sections 1 and 2] and [3, Theorem 7.3 p. 61] in the same way as the exact sequences (13.4) and [13, (1.9)] are related with the spectral sequence associated with a group extension and a module over the extension group, cf. also [12].
References
Brumer, A.: Galois groups of extensions of algebraic number fields with given ramification. Mich. Math. J. 13, 33–40 (1966)
Cegarra, A.M., Garzón, A.R.: Equivariant Brauer groups and cohomology. J. Algebra 296(1), 56–74 (2006). doi:10.1016/j.jalgebra.2005.11.032
Chase, S.U., Rosenberg, A.: Amitsur cohomology and the Brauer group. Mem. Am. Math. Soc. 52, 34–79 (1965)
Childs, L.N.: On normal Azumaya algebras and the Teichmüller cocycle map. J. Algebra 23, 1–17 (1972)
Eilenberg, S., MacLane, S.: Cohomology and Galois theory. I. Normality of algebras and Teichmüller’s cocycle. Trans. Amer. Math. Soc. 64, 1–20 (1948)
Fröhlich, A., Wall, C.: Generalisations of the Brauer group. I Preprint (1971a)
Fröhlich, A., Wall, C.T.C.: Equivariant Brauergroups in algebraic number theory. In: Colloque de Théorie des Nombres (Univ. de Bordeaux, Bordeaux, 1969), Soc. Math. France, Paris, pp. 91–96. Bull. Soc. Math. France, Mém. No. 25 (1971b)
Fröhlich, A., Wall, C.T.C.: Graded monoidal categories. Compos. Math. 28, 229–285 (1974)
Fröhlich, A., Wall, C.T.C.: Equivariant Brauer groups. In: Quadratic forms and their applications (Dublin, 1999), Contemp. Math., vol 272, Amer. Math. Soc., Providence, RI, pp. 57–71 (2000) doi:10.1090/conm/272/04397
Hattori, A.: On groups \(H^{n}(S/R)\) related to the Amitsur cohomology and the Brauer group of commutative rings. Osaka J. Math. 16(2):357–382 (1979). http://projecteuclid.org/euclid.ojm/1200772080
Hochschild, G., Serre, J.P.: Cohomology of group extensions. Trans. Am. Math. Soc. 74, 110–134 (1953)
Huebschmann, J.: Automorphisms of group extensions and differentials in the Lyndon–Hochschild–Serre spectral sequence. J. Algebra 72(2), 296–334 (1981a). doi:10.1016/0021-8693(81)90296-9
Huebschmann, J.: Group extensions, crossed pairs and an eight term exact sequence. J. Reine Angew. Math. 321, 150–172 (1981). doi:10.1515/crll.1981.321.150
Huebschmann, J.: Normality of algebras over commutative rings and the Teichmüller class. I. The absolute theory. J. Homotopy Relat. Struct. (2017). doi:10.1007/s40062-017-0173-3
Huebschmann, J.: Normality of algebras over commutative rings and the Teichmüller class. III. Examples. J. Homotopy Relat. Struct. (2017). doi:10.1007/s40062-017-0175-1
Kanzaki, T.: On generalized crossed product and Brauer group. Osaka J. Math. 5, 175–188 (1968)
Taylor, R.L.: Compound group extensions. I. Continuations of normal homomorphisms. Trans. Am. Math. Soc. 75, 106–135 (1953)
Ulbrich, K.H.: An abstract version of the Hattori–Villamayor–Zelinsky sequences. Sci. Pap. Coll. Gen. Ed. Univ. Tokyo 29(2), 125–137 (1979)
Villamayor, O.E., Zelinsky, D.: Brauer groups and Amitsur cohomology for general commutative ring extensions. J. Pure Appl. Algebra 10(1), 19–55 (1977/78)
Yokogawa, K.: An application of the theory of descent to the \(S\otimes _{R}S\)-module structure of \(S/R\)-Azumaya algebras. Osaka J. Math. 15(1), 21–31 (1978)
Acknowledgements
I am indebted to the referee for a number of valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Tim Porter.
Dedicated to Ronnie Brown on the occasion of his 80th birthday
Support by the Labex CEMPI (ANR-11-LABX-0007-01) is gratefully acknowledged.
Appendix
Appendix
As a service to the reader, we recollect some more material from the theory of stably graded symmetric monoidal categories [6, 8, 9] and use it to illustrate some of the constructions in the present paper.
Recall that an S-progenerator is a faithful finitely generated projective S-module. Given two Q-equivariant Azumaya S-algebras \((A,\tau _A)\) and \((B,\tau _B)\), a (B, A, Q)-bimodule \((M,\tau _M)\) is a (B, A)-bimodule M together with an \(S^tQ\)-module structure \(\tau _M:Q \rightarrow {\text{ Aut }}(M)\) which is compatible with the Q-equivariant structures
in the sense that
The object \((S,Q,\kappa _Q)\) of the category  being given, let \((T,G,\kappa _G)\) be another object of
being given, let \((T,G,\kappa _G)\) be another object of  , and let \((f,\varphi ):(S,Q,\kappa _Q) \rightarrow (T,G,\kappa _G)\) be a morphism in
, and let \((f,\varphi ):(S,Q,\kappa _Q) \rightarrow (T,G,\kappa _G)\) be a morphism in  having \(\varphi :G \rightarrow Q\) surjective, cf. [14, Subsection 3.7].
having \(\varphi :G \rightarrow Q\) surjective, cf. [14, Subsection 3.7].
1.1 Examples of symmetric monoidal categories
-
 : the category of S-modules, a symmetric monoidal category under the operation of tensor product, with S as unit object, and
: the category of S-modules, a symmetric monoidal category under the operation of tensor product, with S as unit object, and  ;
; -
 [6, §2 p. 17], [8, p. 229], [9, §2]: the symmetric monoidal subcategory of
[6, §2 p. 17], [8, p. 229], [9, §2]: the symmetric monoidal subcategory of 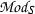 , necessarily a groupoid, whose objects are the S-progenerators, with morphisms only the invertible ones, having S as its unit object and
, necessarily a groupoid, whose objects are the S-progenerators, with morphisms only the invertible ones, having S as its unit object and 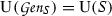
as its unit group;
-
 : the symmetric monoidal subcategory of
: the symmetric monoidal subcategory of  , necessarily group-like, of invertible modules, written in [6, §2 p. 17], [9, §2] as
, necessarily group-like, of invertible modules, written in [6, §2 p. 17], [9, §2] as 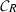 , reproduced in [14, Subsection 3.6];
, reproduced in [14, Subsection 3.6]; -
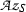 : the symmetric monoidal subcategory of
: the symmetric monoidal subcategory of 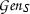 , necessarily a groupoid, having the Azumaya S-algebras as objects, invertible algebra morphisms between Azumaya S-algebras as morphisms, the ground ring S as its unit object, and unit group
, necessarily a groupoid, having the Azumaya S-algebras as objects, invertible algebra morphisms between Azumaya S-algebras as morphisms, the ground ring S as its unit object, and unit group  trivial [6, § 2 p. 18], [8, p. 229], [9, §2];
trivial [6, § 2 p. 18], [8, p. 229], [9, §2]; -
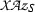 : the quotient category of
: the quotient category of 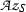 , necessarily a groupoid, having the same objects as
, necessarily a groupoid, having the same objects as 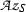 , and having as morphisms \(A \rightarrow B\) between two objects A and B equivalence classes of morphisms \(h :A \rightarrow B\) in
, and having as morphisms \(A \rightarrow B\) between two objects A and B equivalence classes of morphisms \(h :A \rightarrow B\) in 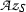 under the equivalence relation $$\begin{aligned} h_1 \sim h_2 :A \rightarrow B \ \text {if}\ h_1=h_2 \circ I_a \ \text {for some}\ a \in \mathrm U(A) \end{aligned}$$
under the equivalence relation $$\begin{aligned} h_1 \sim h_2 :A \rightarrow B \ \text {if}\ h_1=h_2 \circ I_a \ \text {for some}\ a \in \mathrm U(A) \end{aligned}$$[6, §5 p. 43], [9, §2], where the notation \(I_a\) refers to the inner automorphism of A induced by \(a\in \mathrm U(A)\); this category has S as its unit object, and its unit group
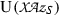 is trivial;
is trivial; -
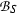 , the Brauer category of the commutative ring S, reproduced in [14, Subsection 3.2];
, the Brauer category of the commutative ring S, reproduced in [14, Subsection 3.2]; -
with respect to the ring homomorphism \(f:S \rightarrow T\), with the obvious interpretations, the relative categories
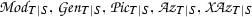 , taken as full subcategories of, respectively,
, taken as full subcategories of, respectively, 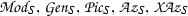 ;
; -
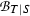 , with respect to the ring homomorphism \(f:S \rightarrow T\), the relative Brauer category, introduced in Subsection 18.3.2 above;
, with respect to the ring homomorphism \(f:S \rightarrow T\), the relative Brauer category, introduced in Subsection 18.3.2 above; -
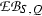 , the equivariant Brauer category
, the equivariant Brauer category 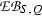 of S relative to the given action of Q on S, written as
of S relative to the given action of Q on S, written as 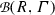 in [6, §5 p. 41] and [9, §3]; its objects are the Q-equivariant Azumaya algebras \((A,\tau )\); given two Q-equivariant Azumaya algebras \((A,\tau _A)\) and \((B,\tau _B)\), a morphism
$$\begin{aligned} {[(M,\tau _M)]:(A,\tau _A) \longrightarrow (B,\tau _B)} \end{aligned}$$
in [6, §5 p. 41] and [9, §3]; its objects are the Q-equivariant Azumaya algebras \((A,\tau )\); given two Q-equivariant Azumaya algebras \((A,\tau _A)\) and \((B,\tau _B)\), a morphism
$$\begin{aligned} {[(M,\tau _M)]:(A,\tau _A) \longrightarrow (B,\tau _B)} \end{aligned}$$in
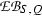 , necessarily an isomorphism in
, necessarily an isomorphism in 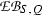 , is an isomorphism class \([(M,\tau _M)]\) of a (B, A, Q)-bimodule \((M,\tau _M:Q \rightarrow {\text{ Aut }}(M))\) whose underlying (B, A)-bimodule M is invertible; the operations of tensor product and that of assigning to a Q-equivariant Azumaya S-algebra its opposite algebra (as a Q-equivariant Azumaya S-algebra) turn
, is an isomorphism class \([(M,\tau _M)]\) of a (B, A, Q)-bimodule \((M,\tau _M:Q \rightarrow {\text{ Aut }}(M))\) whose underlying (B, A)-bimodule M is invertible; the operations of tensor product and that of assigning to a Q-equivariant Azumaya S-algebra its opposite algebra (as a Q-equivariant Azumaya S-algebra) turn 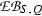 into a group-like symmetric monoidal category having \((S,\kappa _Q)\) is its unit object and
into a group-like symmetric monoidal category having \((S,\kappa _Q)\) is its unit object and 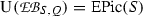 as its unit group [9, §3], [9, Proposition 3.1].
as its unit group [9, §3], [9, Proposition 3.1]. -
 , the relative equivariant Brauer category associated with the morphism
\((f,\varphi )\) in
, the relative equivariant Brauer category associated with the morphism
\((f,\varphi )\) in  ; it has as its objects the Q-equivariant Azumaya algebras \((A,\tau )\) such that the G-equivariant Azumaya algebra \((T\otimes A, \tau ^G)\) that arises by scalar extension has its underlying central T-algebra \(T\otimes A\) isomorphic to a matrix algebra; given two Q-equivariant Azumaya algebras \((A,\tau _A)\) and \((B,\tau _B)\) in
; it has as its objects the Q-equivariant Azumaya algebras \((A,\tau )\) such that the G-equivariant Azumaya algebra \((T\otimes A, \tau ^G)\) that arises by scalar extension has its underlying central T-algebra \(T\otimes A\) isomorphic to a matrix algebra; given two Q-equivariant Azumaya algebras \((A,\tau _A)\) and \((B,\tau _B)\) in 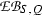 , a morphism
\((A,\tau _A) \rightarrow (B,\tau _B)\) in the associated precategory
, a morphism
\((A,\tau _A) \rightarrow (B,\tau _B)\) in the associated precategory 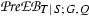 , necessarily an isomorphism in
, necessarily an isomorphism in 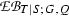 , is a morphism \( [M,\tau _M]:(A,\tau _A) \longrightarrow (B,\tau _B) \) in
, is a morphism \( [M,\tau _M]:(A,\tau _A) \longrightarrow (B,\tau _B) \) in 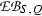 , that is, an isomorphism class of a (B, A, Q)-bimodule \((M,\tau _M:Q \rightarrow {\text{ Aut }}(M))\) whose underlying (B, A)-bimodule M is invertible, such that, furthermore, the resulting \(T^{t}G\)-module \(T \otimes M\) is free as a T-module. We then take
, that is, an isomorphism class of a (B, A, Q)-bimodule \((M,\tau _M:Q \rightarrow {\text{ Aut }}(M))\) whose underlying (B, A)-bimodule M is invertible, such that, furthermore, the resulting \(T^{t}G\)-module \(T \otimes M\) is free as a T-module. We then take 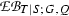 to be the resulting subcategory of
to be the resulting subcategory of 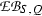 generated by
generated by 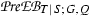 , that is, we define morphisms and composition of morphisms as finite strings in
, that is, we define morphisms and composition of morphisms as finite strings in 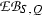 , of morphisms in
, of morphisms in 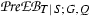 , and we define the monoidal structure, the operation of inverse, and the unit object as in
, and we define the monoidal structure, the operation of inverse, and the unit object as in 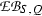 . The resulting category
. The resulting category 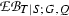 is a group-like symmetric monoidal category and has
is a group-like symmetric monoidal category and has 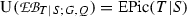 .
.
1.2 Examples of stably Q-graded symmetric monoidal categories
-
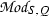 , a stably Q-graded symmetric monoidal category that arises from
, a stably Q-graded symmetric monoidal category that arises from 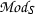 as follows: Given two S-modules M and N, a morphism
\(M\rightarrow N\)
of
S-modules of grade
\(x \in Q\) is a pair \((\varphi ,x)\) having \(\varphi :M \rightarrow N\) a morphism over \(R=S^Q\) such that \(\varphi (sy)=({}^x\!s)y\) (\(s\in S, y \in M\)) [8, p. 229], [9, §2].
as follows: Given two S-modules M and N, a morphism
\(M\rightarrow N\)
of
S-modules of grade
\(x \in Q\) is a pair \((\varphi ,x)\) having \(\varphi :M \rightarrow N\) a morphism over \(R=S^Q\) such that \(\varphi (sy)=({}^x\!s)y\) (\(s\in S, y \in M\)) [8, p. 229], [9, §2].
Enhancing each of the categories  in Subsection 19.1 above to a stably Q-graded symmetric monoidal category
in Subsection 19.1 above to a stably Q-graded symmetric monoidal category  in the same was as enhancing the category
in the same was as enhancing the category  of S-modules to the stably Q-graded symmetric monoidal category
of S-modules to the stably Q-graded symmetric monoidal category  just explained yields the following stably Q-graded symmetric monoidal categories:
just explained yields the following stably Q-graded symmetric monoidal categories:
-
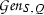 , written in [9] as
, written in [9] as 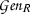 ;
; -
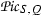 , written in [9, §3] as
, written in [9, §3] as 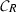 , reproduced in [14, Subsection 3.6];
, reproduced in [14, Subsection 3.6]; -
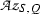 , written in [9, §2] as
, written in [9, §2] as 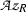 ;
; -
 , written in [6, §5 p. 43] as
, written in [6, §5 p. 43] as 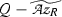 and in [9, §2] as
and in [9, §2] as 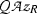 (beware: the notation Q in [op. cit.] has nothing to do with our notation Q for a group, and the tilde-notation in [6, §5 p. 43] refers to the additional structure of a twisting and need not concern us here); morphisms are now enhanced via the Q-grading, that is to say, a morphism \(([h],x):A \rightarrow B\) in
(beware: the notation Q in [op. cit.] has nothing to do with our notation Q for a group, and the tilde-notation in [6, §5 p. 43] refers to the additional structure of a twisting and need not concern us here); morphisms are now enhanced via the Q-grading, that is to say, a morphism \(([h],x):A \rightarrow B\) in 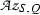 of grade \(x\in Q\) has [h] an equivalence class of an isomorphism \(h:A \rightarrow B\) of algebras over \(R=S^Q\) such that (h, x) is, furthermore, a morphism in
of grade \(x\in Q\) has [h] an equivalence class of an isomorphism \(h:A \rightarrow B\) of algebras over \(R=S^Q\) such that (h, x) is, furthermore, a morphism in 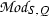 of grade \(x\in Q\);
of grade \(x\in Q\); -
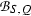 , the stably Q-graded Brauer category associated with the commutative ring S and the Q-action \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\) on S, reproduced in [14, Subsection 3.5].
, the stably Q-graded Brauer category associated with the commutative ring S and the Q-action \(\kappa _Q:Q \rightarrow {\text{ Aut }}(S)\) on S, reproduced in [14, Subsection 3.5].
The morphism \({(f,\varphi ):(S,Q,\kappa _Q) \rightarrow (T,G,\kappa _G)}\) in  having \(\varphi \) surjective being given, similarly to the construction of the category
having \(\varphi \) surjective being given, similarly to the construction of the category  in Subsection 18.3 above, for each of the stably Q-graded symmetric monoidal categories
in Subsection 18.3 above, for each of the stably Q-graded symmetric monoidal categories

the stably Q-graded symmetric monoidal category  is the subcategory that arises from the ambient category
is the subcategory that arises from the ambient category  in essentially the same way as
in essentially the same way as  arises from the ambient category
arises from the ambient category  save that there is no need to pass through a corresponding precategory: The objects of
save that there is no need to pass through a corresponding precategory: The objects of  are those objects C of
are those objects C of  that have the property that \(T \otimes C\) is free as a T-module, and
that have the property that \(T \otimes C\) is free as a T-module, and  is the respective full subcategory of
is the respective full subcategory of  . Likewise, for the stably Q-graded symmetric monoidal categories
. Likewise, for the stably Q-graded symmetric monoidal categories  and
and  , the stably Q-graded symmetric monoidal category
, the stably Q-graded symmetric monoidal category  arises as the subcategory that has as its objects Azumaya S-algebras A such that \(T\otimes A\) is a matrix algebra over T, and
arises as the subcategory that has as its objects Azumaya S-algebras A such that \(T\otimes A\) is a matrix algebra over T, and  is the corresponding full subcategory of
is the corresponding full subcategory of  and
and  that of
that of  . Now, with
. Now, with  substituted for
substituted for  , the exact sequence [14, (3.10)] yields the exact sequence (18.12).
, the exact sequence [14, (3.10)] yields the exact sequence (18.12).
Remark 19.1
For an object of  , that is, for a faithful finitely generated projective S-module M, the group \({\text{ Aut }}(M,Q)\) introduced in [14, Section 7] is canonically isomorphic to the group
, that is, for a faithful finitely generated projective S-module M, the group \({\text{ Aut }}(M,Q)\) introduced in [14, Section 7] is canonically isomorphic to the group  .
.
1.3 The standard constructions revisited
The endomorphism functor  induces an exact sequence
induces an exact sequence

of abelian monoids [6, §5 p. 38], [8, Introduction], [9, §3]. This yields \({\text{ Pic }}(S)\) as the maximal subgroup of the abelian monoid  and recovers the standard construction of \(\mathrm B(S)\), cf. [14, Subsection 4.2], as the cokernel of the homomorphism \({\text{ End }}\) of abelian monoids, the cokernel of a morphism of monoids being suitably interpreted (in terms of the associated equivalence relation and “cofinality”, cf. [8, §12]). The obvious functor
and recovers the standard construction of \(\mathrm B(S)\), cf. [14, Subsection 4.2], as the cokernel of the homomorphism \({\text{ End }}\) of abelian monoids, the cokernel of a morphism of monoids being suitably interpreted (in terms of the associated equivalence relation and “cofinality”, cf. [8, §12]). The obvious functor  induces the isomorphism
induces the isomorphism  of abelian groups [6, §5 p. 38], [9, §3, Theorem 3.2 (i)] quoted in [14, Subsection 4.2].
of abelian groups [6, §5 p. 38], [9, §3, Theorem 3.2 (i)] quoted in [14, Subsection 4.2].
Likewise, the endomorphism functor  induces an exact sequence
induces an exact sequence

of abelian monoids [6, §5 p. 38], [8, Introduction], [9, §3]. This yields \(\mathrm {EPic}(S,Q)\) as the maximal subgroup of the abelian monoid  and recovers the standard construction of \(\mathrm {EB}(S,Q)\), cf. [14, Section 9], as the cokernel of the corresponding homomorphism \({\text{ End }}\) of abelian monoids. The obvious functor
and recovers the standard construction of \(\mathrm {EB}(S,Q)\), cf. [14, Section 9], as the cokernel of the corresponding homomorphism \({\text{ End }}\) of abelian monoids. The obvious functor  induces an isomorphism
induces an isomorphism  of abelian groups [6, §5 p. 38], [9, § 3, Theorem 3.2 (i)], that is, equivariant Brauer equivalence is equivalent to equivariant Morita equivalence. Moreover, that obvious functor \(\varOmega \) factors as
of abelian groups [6, §5 p. 38], [9, § 3, Theorem 3.2 (i)], that is, equivariant Brauer equivalence is equivalent to equivariant Morita equivalence. Moreover, that obvious functor \(\varOmega \) factors as

and the functor  induces the injection
induces the injection

of abelian groups spelled out as [14, (8.4)].
Recall that, given a stably Q-graded category  , the notation
, the notation  refers to the monoid
refers to the monoid  , viewed as a Q-monoid, cf. [14, Subsection 3.4]. The functor
, viewed as a Q-monoid, cf. [14, Subsection 3.4]. The functor  induces, furthermore, a homomorphism
induces, furthermore, a homomorphism

of monoids [9, §3]. Indeed, let M be an object of  . By construction, the grading homomorphism
. By construction, the grading homomorphism  is surjective if and only if the isomorphism class of M in
is surjective if and only if the isomorphism class of M in  is fixed under Q. Hence an object M of
is fixed under Q. Hence an object M of  whose isomorphism class in
whose isomorphism class in  is fixed under Q determines the exact sequence
is fixed under Q determines the exact sequence

plainly congruent to the exact sequence [14, (7.4)]; in particular, the group  is canonically isomorphic to the group \({\text{ Aut }}(M,Q)\), cf. [14, (7.3)]. Now, for any object M of
is canonically isomorphic to the group \({\text{ Aut }}(M,Q)\), cf. [14, (7.3)]. Now, for any object M of  , the groups
, the groups  , and \(\mathrm U({\text{ End }}_S(M))\) coincide, and the induced action of
, and \(\mathrm U({\text{ End }}_S(M))\) coincide, and the induced action of  on \({\text{ End }}_S(M)\) yields a commutative diagram of the kind
on \({\text{ End }}_S(M)\) yields a commutative diagram of the kind

and hence an induced Q-normal structure \(Q \rightarrow {\text{ Out }}({\text{ End }}_S(M))\) on the split algebra \({\text{ End }}_S(M)\). Thus the endomorphism functor  induces an exact sequence
induces an exact sequence

of abelian monoids [9, §3] which, in turn, recovers the standard construction of the crossed Brauer group \(\mathrm {XB}(S,Q)\) of S relative to Q given in [14, Section 8.1]. The unit object of  is represented by \((S,\kappa _Q)\). This kind of construction is given in [6, Theorem 4 p. 43], [9, Section 3, a few lines before Theorem 3.2] (the cokernel of \({\text{ End }}\) being written as \(QB(R,\varGamma )\)). In general, for the “crossed” versions, the equivalence between Brauer and Morita equivalence persists only when the group Q is finite, that is the canonical homomorphism
is represented by \((S,\kappa _Q)\). This kind of construction is given in [6, Theorem 4 p. 43], [9, Section 3, a few lines before Theorem 3.2] (the cokernel of \({\text{ End }}\) being written as \(QB(R,\varGamma )\)). In general, for the “crossed” versions, the equivalence between Brauer and Morita equivalence persists only when the group Q is finite, that is the canonical homomorphism  of abelian groups given as [14, (8.4)] is injective, see [14, Theorem 8.10 (i)], but to prove that \(\theta \) is surjective we need the additional hypothesis that Q be a finite group, see [14, Theorem 8.10 (iii)].
of abelian groups given as [14, (8.4)] is injective, see [14, Theorem 8.10 (i)], but to prove that \(\theta \) is surjective we need the additional hypothesis that Q be a finite group, see [14, Theorem 8.10 (iii)].
The above constructions, applied, with respect to the morphism \((f,\varphi )\) in  , to the functors
, to the functors  and
and  , yield the exact sequences
, yield the exact sequences

of abelian monoids. These recover the standard constructions of the abelian groups \(\mathrm B_{\mathrm {fr}}(T|S), \mathrm {EB}_{\mathrm {fr}}(T|S;G,Q)\), and \(\mathrm {XB}_{\mathrm {fr}}(T|S;G,Q)\), cf. Subsection 18.3.1 above.
Rights and permissions
About this article
Cite this article
Huebschmann, J. Normality of algebras over commutative rings and the Teichmüller class. II.. J. Homotopy Relat. Struct. 13, 71–125 (2018). https://doi.org/10.1007/s40062-017-0174-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40062-017-0174-2
Keywords
- Teichmüller cocycle
- Crossed module
- Crossed pair
- Normal algebra
- Crossed product
- Deuring embedding problem
- Group cohomology
- Galois theory of commutative rings
- Azumaya algebra
- Brauer group
- Galois cohomology
- Non-commutative Galois theory
- Non-abelian cohomology





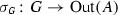 on A coincide.
on A coincide.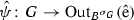 on
on 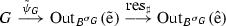
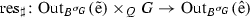 induced by the obvious restriction homomorphism
induced by the obvious restriction homomorphism 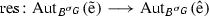 .
. : the category of S-modules, a symmetric monoidal category under the operation of tensor product, with S as unit object, and
: the category of S-modules, a symmetric monoidal category under the operation of tensor product, with S as unit object, and  ;
; [
[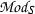 , necessarily a groupoid, whose objects are the S-progenerators, with morphisms only the invertible ones, having S as its unit object and
, necessarily a groupoid, whose objects are the S-progenerators, with morphisms only the invertible ones, having S as its unit object and 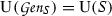
 : the symmetric monoidal subcategory of
: the symmetric monoidal subcategory of  , necessarily group-like, of invertible modules, written in [
, necessarily group-like, of invertible modules, written in [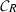 , reproduced in [
, reproduced in [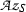 : the symmetric monoidal subcategory of
: the symmetric monoidal subcategory of 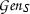 , necessarily a groupoid, having the Azumaya S-algebras as objects, invertible algebra morphisms between Azumaya S-algebras as morphisms, the ground ring S as its unit object, and unit group
, necessarily a groupoid, having the Azumaya S-algebras as objects, invertible algebra morphisms between Azumaya S-algebras as morphisms, the ground ring S as its unit object, and unit group  trivial [
trivial [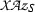 : the quotient category of
: the quotient category of 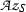 , necessarily a groupoid, having the same objects as
, necessarily a groupoid, having the same objects as 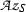 , and having as morphisms
, and having as morphisms 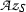 under the equivalence relation
under the equivalence relation 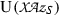 is trivial;
is trivial;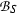 , the Brauer category of the commutative ring S, reproduced in [
, the Brauer category of the commutative ring S, reproduced in [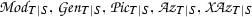 , taken as full subcategories of, respectively,
, taken as full subcategories of, respectively, 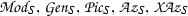 ;
;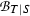 , with respect to the ring homomorphism
, with respect to the ring homomorphism 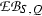 , the equivariant Brauer category
, the equivariant Brauer category 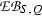 of S relative to the given action of Q on S, written as
of S relative to the given action of Q on S, written as 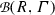 in [
in [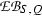 , necessarily an isomorphism in
, necessarily an isomorphism in 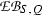 , is an isomorphism class
, is an isomorphism class 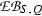 into a group-like symmetric monoidal category having
into a group-like symmetric monoidal category having 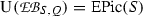 as its unit group [
as its unit group [ , the relative equivariant Brauer category associated with the morphism
, the relative equivariant Brauer category associated with the morphism
 ; it has as its objects the Q-equivariant Azumaya algebras
; it has as its objects the Q-equivariant Azumaya algebras 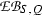 , a morphism
, a morphism
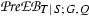 , necessarily an isomorphism in
, necessarily an isomorphism in 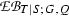 , is a morphism
, is a morphism 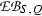 , that is, an isomorphism class of a (B, A, Q)-bimodule
, that is, an isomorphism class of a (B, A, Q)-bimodule 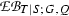 to be the resulting subcategory of
to be the resulting subcategory of 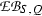 generated by
generated by 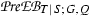 , that is, we define morphisms and composition of morphisms as finite strings in
, that is, we define morphisms and composition of morphisms as finite strings in 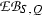 , of morphisms in
, of morphisms in 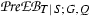 , and we define the monoidal structure, the operation of inverse, and the unit object as in
, and we define the monoidal structure, the operation of inverse, and the unit object as in 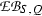 . The resulting category
. The resulting category 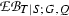 is a group-like symmetric monoidal category and has
is a group-like symmetric monoidal category and has 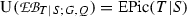 .
.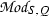 , a stably Q-graded symmetric monoidal category that arises from
, a stably Q-graded symmetric monoidal category that arises from 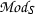 as follows: Given two S-modules M and N, a morphism
as follows: Given two S-modules M and N, a morphism
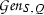 , written in [
, written in [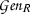 ;
;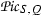 , written in [
, written in [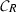 , reproduced in [
, reproduced in [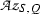 , written in [
, written in [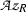 ;
; , written in [
, written in [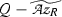 and in [
and in [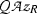 (beware: the notation Q in [op. cit.] has nothing to do with our notation Q for a group, and the tilde-notation in [
(beware: the notation Q in [op. cit.] has nothing to do with our notation Q for a group, and the tilde-notation in [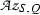 of grade
of grade 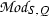 of grade
of grade 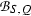 , the stably Q-graded Brauer category associated with the commutative ring S and the Q-action
, the stably Q-graded Brauer category associated with the commutative ring S and the Q-action