The mod 2 dual Steenrod algebra as a subalgebra of the mod 2 dual Leibniz-Hopf algebra

Abstract

The mod 2 Steenrod algebra $\mathcal {A}_2$ can be defined as the quotient of the mod 2 Leibniz–Hopf algebra $\mathcal {F}_2$ by the Adem relations. Dually, the mod 2 dual Steenrod algebra $\mathcal {A}_2^*$ can be thought of as a sub-Hopf algebra of the mod 2 dual Leibniz–Hopf algebra $\mathcal {F}_2^*$. We study $\mathcal {A}_2^*$ and $\mathcal {F}_2^*$ from this viewpoint and give generalisations of some classical results in the literature.

1 The mod 2 Leibniz–Hopf algebra and its dual

Let $\mathcal {F}_2$ be the free associative algebra over $\mathbb {F}_2$ generated by the indeterminates $S^1, S^2, S^3, \ldots$ of degree $|S^i|=i$. We often denote the unit 1 by $S^0$. This algebra is equipped with a co-commutative co-product given by

$$\begin{aligned} \Delta (S^n) = \sum _{i=0}^n S^i \otimes S^{n-i}, \end{aligned}$$

(1)

which makes it a graded connected Hopf algebra. This algebra $\mathcal {F}_2$ is often called the mod 2 Leibniz–Hopf algebra. As an $\mathbb {F}_2$-module, $\mathcal {F}_2$ has the following canonical basis:

$$\begin{aligned} \{ S^I:=S^{i_1}S^{i_2}\cdots S^{i_n} \mid I=(i_1,i_2,\ldots ,i_n)\in \mathbb {N}^n, 0\le n <\infty \}, \end{aligned}$$

where we regard $S^I=1$ when $n=0$.

Note that the integral counterpart of $\mathcal {F}_2$ is called the Leibniz–Hopf algebra and is isomorphic to the ring of non-commutative symmetric functions [7] and the Solomon Descent algebra [17]. Its graded dual is the ring of quasi-symmetric functions with the outer co-product, which has been studied by Hazewinkel, Malvenuto, and Reutenauer in [8,9,10,11,12].

The mod 2 Steenrod algebra $\mathcal {A}_2$ is defined to be the quotient Hopf algebra of $\mathcal {F}_2$ by the ideal generated by the Adem relations:

$$\begin{aligned} S^i S^j - \sum _{k=0}^{\lfloor i/2 \rfloor } {{j-k-1}\atopwithdelims (){i-2k}} S^{i+j-k}S^k. \end{aligned}$$

(2)

Denote the quotient map by $\pi : \mathcal {F}_2\rightarrow \mathcal {A}_2$ and $Sq^i=\pi (S^i)$. It is well-known (see, for example, [18]) that the admissible monomials

$$\begin{aligned} \{Sq^J:=Sq^{j_1}Sq^{j_2}\cdots Sq^{j_n} \mid J=(j_1,j_2,\ldots ,j_n)\in \mathbb {N}_{>0}^n, 0\le n <\infty , j_{k-1} \ge 2 j_{k} \forall k\} \end{aligned}$$

form a module basis for $\mathcal {A}_2$. We will adhere to this purely algebraic definition and will not use any other known facts about $\mathcal {A}_2$.

By taking the graded dual of $\pi$, we obtain the following inclusion of Hopf algebras

$$\begin{aligned} \pi ^*: \mathcal {A}_2^* \rightarrow \mathcal {F}_2^*. \end{aligned}$$

$\mathcal {F}_2^*$ is given a module basis $S_I$ dual to $S^I$, that is,

$$\begin{aligned} \langle S^{I'}, S_I \rangle = {\left\{ \begin{array}{ll} 1 &{} (I=I') \\ 0 &{} (I\ne I') \end{array}\right. }. \end{aligned}$$

Similarly, we have the dual basis $\{Sq_J \mid J \text { admissible} \}$ for $\mathcal {A}_2^*$ determined by

$$\begin{aligned} \langle Sq^{J'}, Sq_J \rangle = {\left\{ \begin{array}{ll} 1 &{} (J=J') \\ 0 &{} (J\ne J') \end{array}\right. }. \end{aligned}$$

The commutative product among the basis elements in $\mathcal {F}_2^*$ is given by the overlapping shuffle product (see §2) and the co-product is given by

$$\begin{aligned} \Delta (S_{a_1,\ldots ,a_n})=S_{a_1,\ldots ,a_n} \otimes 1 + 1 \otimes S_{a_1,\ldots ,a_n}+ \sum _{i=1}^{n-1} S_{a_1,\ldots ,a_i} \otimes S_{a_{i+1},\ldots ,a_n}. \end{aligned}$$

(3)

The purpose of this paper is to deduce some of the classical results on $\mathcal {A}_2^*$ and its generalisations by considering it as a subalgebra of $\mathcal {F}_2^*$. We are particularly interested in the following problems.

Problem 1

• (i) Determine the coefficients in

  $$\begin{aligned} \pi ^*(Sq_J) = \sum _{I} C^I_J S_I \end{aligned}$$

  (4)

  for all admissible sequences J. This is important since in the dual it is equivalent to computing the coefficients of the Adem relations

  $$\begin{aligned} Sq^I = \sum _{J:\text {admissible}} C^I_J Sq^J \end{aligned}$$

  (5)

  for all sequences I.

• (ii) Give an expansion of the dual Milnor bases in terms of the dual admissible monomial bases, i.e., determine the coefficient $B^L_J$ in

  $$\begin{aligned} \xi ^L = \sum _{J:\text {admissible}} B^L_J Sq_J, \end{aligned}$$

  where $\xi _n=Sq_{2^{n-1},2^{n-2}\cdots 2^1,2^0}$ and $\xi ^L=\xi _1^{l_1}\xi _2^{l_2}\cdots \xi _n^{l_n}$ for $L=(l_1,l_2,\ldots , l_n)$.

• (iii) Generalise Milnor’s conjugation formula [13] in $\mathcal {A}_2^*$ to $\mathcal {F}_2^*$. The formula for $\mathcal {A}_2^*$ is:

  $$\begin{aligned} \chi (\xi _n)= \sum _\alpha \prod _{i=1}^{l(\alpha )} \xi _{\alpha (i)}^{2^{\sigma (i)}}, \end{aligned}$$

  where $\alpha =(\alpha (1)|\alpha (2)|\ldots |\alpha (l(\alpha ))$ runs through all the compositions of the integer n and $\sigma (i)=\sum _{j=1}^{i-1} \alpha (j)$.

Several different methods are known for resolving (i) and (ii) (see for example, [15, 19]), but our argument (Sect. 4) is new in that it is purely combinatorial using the overlapping shuffle product on $\mathcal {F}_2^*$. We implemented our algorithm into a Maple code [16]. In Sect. 5 we discuss the conjugation (or antipode) in $\mathcal {F}_2^*$ and give an answer to (iii). Finally, we give an explicit duality between the conjugation invariants in $\mathcal {F}_2$ and $\mathcal {F}_2^*$ in Sect. 6.

2 Overlapping Shuffle product

We recall the definition of the overlapping shuffle product ([2, Section 2],[8]). Let $\mathcal {W}$ be the set of finite sequences of natural numbers:

$$\begin{aligned} \mathcal {W}= \{ (i_1,i_2,\ldots ,i_n) \mid 0\le n <\infty \}. \end{aligned}$$

Note that we allow the length 0 sequence. Consider the $\mathbb {F}_2$-module $\mathbb {F}_2\langle \mathcal {W}\rangle$ freely generated by $\mathcal {W}$. For a sequence $I=(i_1,i_2,\ldots ,i_n)$, denote its tail partial sequence $(i_k,i_{k+1},\ldots ,i_n)$ by $I_k$. When $n<k$, we regard $I_k$ as the length 0 sequence. We use the convention

$$\begin{aligned}&(a_1,a_2,\ldots ,a_k,(b_1,\ldots ,b_i)+(c_1,\ldots ,c_j))\\&\quad :=(a_1,a_2,\ldots ,a_k,b_1,\ldots ,b_i) +(a_1,a_2,\ldots ,a_k,c_1,\ldots ,c_j). \end{aligned}$$

The overlapping shuffle product on $\mathbb {F}_2\langle \mathcal {W}\rangle$ is defined as follows:

Definition 1

For $A=(a_1,a_2,\ldots ,a_n)$ and $B=(b_1,b_2,\ldots ,b_m)$, define their product inductively by

$$\begin{aligned} A\cdot B:= {\left\{ \begin{array}{ll} A &{} (m=0) \\ B &{} (n=0) \\ \sum _{0\le i \le n} (a_1,\ldots , a_i, b_1, A_{i+1}\cdot B_2)\\ \quad + \sum _{1\le i \le n} (a_1,\ldots , a_i+b_1, A_{i+1}\cdot B_2) &{} (\text {otherwise}). \end{array}\right. } \end{aligned}$$

The product on $\mathbb {F}_2\langle \mathcal {W}\rangle$ is defined by the linear extension of the above.

We say a term in $A\cdot B$ is a-first if there exists k such that $a_k$ goes¹ to an entry to the left of $b_k$ and $a_i$ goes to the same entry as $b_i$ (that is, the entry makes $a_i+b_i$) for all $i<k$. For example, $(a_1+b_1,a_2,b_2,b_3,a_3)$ is a-first while $(a_1+b_1,b_2,a_2,a_3,b_3)$ is not. Observe that

Lemma 1

For equal length sequences, we have

$$\begin{aligned} (a_1,\ldots ,a_n) \cdot (b_1,\ldots ,b_n)= (a_1+b_1,\ldots ,a_n+b_n) + Z+ \tau (Z), \end{aligned}$$

where Z is a sum of a-first terms and $\tau$ flips the occurrence of $a_i$ and $b_i$ for all i. In particular, the product is commutative.

Example 1

$$\begin{aligned} (a_1,a_2)\cdot (b_1,b_2)&=(a_1+b_1,a_2+b_2) \\&\quad +(a_1+b_1,a_2,b_2)+(a_1,b_1,a_2+b_2)+(a_1,b_1+a_2,b_2)\\&\quad +(a_1,a_2,b_1,b_2)+(a_1,b_1,a_2,b_2)+(a_1,b_1,b_2,a_2) \\&\quad +(b_1+a_1,b_2,a_2)+(b_1,a_1,b_2+a_2)+(b_1,a_1+b_2,a_2)\\&\quad +(b_1,b_2,a_1,a_2)+(b_1,a_1,b_2,a_2)+(b_1,a_1,a_2,b_2), \end{aligned}$$

where the second line consists of a-first terms and the third line is the $\tau$-image of the second line.

Corollary 1

For $A=(a_1,\ldots ,a_n)$,

$$\begin{aligned} A\cdot A=(2a_1,\ldots ,2a_n), \quad A^{2^m}=(2^m a_1,\ldots ,2^m a_n). \end{aligned}$$

Proof

In this case, the flip map $\tau$ in Lemma 1 is the identity. $\square$

It is easy to see from the duality relation $\langle S_I S_J, S^K \rangle =\langle S_I\otimes S_J, \Delta (S^K) \rangle$ that the product on $\mathcal {F}_2^*$ dual to (1) is given by $S_I S_J= \sum _{K\in I\cdot J} S_K$.

3 Dual Steenrod algebra as a sub-Hopf algebra of $\mathcal {F}_2^*$

To identify the image of the inclusion $\pi ^*:\mathcal {A}_2^* \rightarrow \mathcal {F}_2^*$, we prove some lemmas in this section. Let $\xi _n=Sq_{2^{n-1}, 2^{n-2}, \ldots , 2^0}$.

Lemma 2

(cf. [2, 19]) We have

$$\begin{aligned} \pi ^*(Sq_{2^n})= & {} S_{2^n}, \\ \pi ^*(\xi _n)= & {} S_{2^{n-1}, 2^{n-2}, \ldots , 2^0}. \end{aligned}$$

Proof

For the first equation, we have to show that for any non-admissible sequence I, the right-hand side of

$$\begin{aligned} Sq^I = \sum _{J:\text {admissible}} C^I_J Sq^J \end{aligned}$$

does not contain $Sq^{2^n}$. If there exists such an I, we can assume it has length two, that is, $I=(i,j)$. (Because the right-hand side is obtained by successively applying the length two relations.) By the Adem relations in Eq. (2), we have $i+j=2^n$ and

$$\begin{aligned} 1\equiv \left( {\begin{array}{c}j-1\\ i\end{array}}\right) \equiv \left( {\begin{array}{c}2^n-1-i\\ i\end{array}}\right) \mod 2. \end{aligned}$$

However, the binary expressions of $2^n-1-i$ and i are complementary and the binary expression of $2^n-1-i$ contains at least one digit with 0. Hence, by Lucas’ Theorem, we have $\left( {\begin{array}{c}2^n-1-i\\ i\end{array}}\right) \equiv 0 \mod 2$; we arrive at a contradiction.

For the second equation, suppose that there exists an $I=(i,j)$ such that $i < 2j$ and

$$\begin{aligned} Sq^{i,j} = \sum _{k=0}^{\lfloor i/2 \rfloor } {{j-k-1}\atopwithdelims (){i-2k}} Sq^{i+j-k} Sq^k \end{aligned}$$

contains $Sq^{2^{n-k}}$ or $Sq^{2^{n-k}}Sq^{2^{n-k-1}}$ as a summand. The former case is already ruled out by the first equation. For the latter case to happen, we should have

$$\begin{aligned} i+j=2^{n-k}+2^{n-k-1}, \quad \lfloor i/2 \rfloor \ge 2^{n-k-1}. \end{aligned}$$

But this implies $j\le 2^{n-k-1}$ so $i\ge 2j$; we arrive at a contradiction. $\square$

Put $\bar{\xi }_n=\pi ^*(\xi _n) = S_{2^{n-1}, 2^{n-2}, \ldots , 2^0}$. We denote by $\widetilde{\mathcal {A}}_2^*$ the subalgebra of $\mathcal {F}_2^*$ generated by $\{\bar{\xi }_n \mid 0<n \}$. For a sequence $L=(l_1,l_2,\ldots ,l_n)$ of non-negative integers, we denote $\bar{\xi }_1^{l_1} \bar{\xi }_2^{l_2} \cdots \bar{\xi }_n^{l_n}$ by $\bar{\xi }^L$. Then, the monomials $\bar{\xi }^L$ span $\widetilde{\mathcal {A}}_2^*$. Now, we identify $\widetilde{\mathcal {A}}_2^*$ with $\mathrm {Im}(\pi ^*)$.

Recall the definition of the excess vector of an admissible sequence $J=(j_1,j_2,\ldots ,j_n)$:

$$\begin{aligned} \gamma (j_1,j_2,\ldots ,j_n)=(j_1-2j_2, j_2-2j_3,\ldots ,j_{n-1}-2j_n,j_n). \end{aligned}$$

This gives a bijection between admissible sequences and sequences of non-negative integers. The inverse is given by

$$\begin{aligned} \gamma ^{-1}(l_1,l_2,\ldots ,l_n) = (l_1+2l_2+2^2l_3+\cdots +2^{n-1}l_n,\ldots ,l_{n-1}+2l_n,l_n). \end{aligned}$$

We put the right lexicographic order on $\mathcal {W}$, i.e.,

$$\begin{aligned} (a_1,a_2,\ldots ,a_n)> (b_1,b_2,\ldots ,b_m) \Leftrightarrow (n>m) \text { or } (\exists k, a_k>b_k \text { and } a_i=b_i \forall i>k). \end{aligned}$$

This induces an ordering on the basis elements $S_I$ which is compatible with the overlapping shuffle product. Observe that the lowest term in the product $S_I \cdot S_{I'}$ for $I=(i_1,i_2,\ldots )$ and $I'=(i'_1,i'_2,\ldots )$ is $S_{(i_1+i'_1,i_2+i'_2,\ldots )}$.

Lemma 3

For an admissible sequence J,

$$\begin{aligned} \langle \bar{\xi }^{\gamma (J)}, S^I \rangle = {\left\{ \begin{array}{ll} 1 &{} (I=J) \\ 0 &{} (I<J). \end{array}\right. } \end{aligned}$$

Proof

We proceed by induction on $J=(j_1,\ldots ,j_n)$. Put $J'=(j_1-2^{n-1},j_2-2^{n-2},\ldots ,j_n-2^0)$. Then by induction hypothesis,

$$\begin{aligned} \bar{\xi }^{\gamma (J')}=S_{J'} + (\text {terms higher than } S_{J'}). \end{aligned}$$

It follows that

$$\begin{aligned} \bar{\xi }^{\gamma (J)}= & {} \bar{\xi }^{\gamma (J')} \cdot \bar{\xi }_n\\= & {} (S_{J'} + (\text {terms higher than } S_{J'}))\cdot S_{2^{n-1},2^{n-2},\ldots ,2^0} \\= & {} S_{J} + (\text {terms higher than } S_J). \end{aligned}$$

$\square$

By this upper-triangularity, the monomials $\bar{\xi }^L$ are linearly independent and we have

Theorem 1

$$\begin{aligned} \mathrm {Im}(\pi ^*) = \widetilde{\mathcal {A}}_2^* = \mathbb {F}_2[\bar{\xi }_1,\bar{\xi }_2,\ldots ,]. \end{aligned}$$

Proof

By Lemma 3 in each degree $\widetilde{\mathcal {A}}_2^*$ has the same dimension as $\mathcal {A}_2^*$ (the number of admissible sequences). $\square$

This is nothing but the well-known fact:

Corollary 2

[13]

$$\begin{aligned} \mathcal {A}_2^*=\mathbb {F}_2[\xi _1,\xi _2,\ldots ,], \end{aligned}$$

where

$$\begin{aligned} \xi ^{\gamma (J)}= Sq_J + (\text {terms higher than}\; Sq_J). \end{aligned}$$

4 Computation with $\pi ^*$

Recall from [19, Section 4] the linear left inverse $r:\mathcal {F}_2^* \rightarrow \mathcal {A}_2^*$ of $\pi ^*$:

$$\begin{aligned} r(S_I)={\left\{ \begin{array}{ll} Sq_I &{} (I:\text {admissible}) \\ 0 &{}(\text {otherwise}). \end{array}\right. } \end{aligned}$$

For (ii) of Problem 1, we can compute

$$\begin{aligned} \xi ^{(l_1,l_2,\ldots , l_n)}= & {} r\pi ^*(\xi ^{(l_1,l_2,\ldots ,l_n)})\nonumber \\= & {} r({\bar{\xi }}_{1}^{l_1}{\bar{\xi }}_{2}^{l_2}\cdots {\bar{\xi }}_{n}^{l_n})\nonumber \\= & {} r((S_{2^0})^{l_1} (S_{2^1, 2^0})^{l_2}\cdots (S_{2^{n-1}, 2^{n-2}, \ldots , 2^0})^{l_n}) \end{aligned}$$

(6)

and it reduces to computing admissible sequences occurring in the overlapping shuffle product.

For (i) of Problem 1, by Corollary 2 we have

$$\begin{aligned} \pi ^*(\xi ^{\gamma (J)})=\pi ^*(Sq_J + (\text {terms higher than} \,Sq_J)) \end{aligned}$$

and the left-hand side can be computed by the overlapping shuffle product. Thus, we can compute inductively the coefficients $C^I_J$ in

$$\begin{aligned} \pi ^*(Sq_J) = \sum _{I} C^I_J S_I. \end{aligned}$$

We implemented the algorithm into a Maple code [16].

Example 2

We demonstrate the above algorithm in low degrees. First, compute $\pi ^*$-image of monomials $\xi ^L$:

$$\begin{aligned} \pi ^*(\xi _2^2)&= S_{2, 1} S_{2, 1}=S_{4, 2}\\ \pi ^*(\xi _1^3\xi _2)&=(S_3+S_{1, 2}+S_{2, 1})S_{2, 1}\\&=S_{5, 1}+S_{4, 2}+S_{3, 3}+S_{2, 4}+S_{2, 3, 1}+S_{1, 4, 1}\\&\quad +\,S_{3, 1, 2}+S_{2, 2, 2}+S_{1, 2, 3}+S_{2, 1, 2, 1}+S_{1, 2, 1, 2} \\ \pi ^*(\xi _1^6)&= S_{6}+S_{4,2}+S_{2,4}. \end{aligned}$$

Taking r on the both sides of equations, we obtain

$$\begin{aligned} \xi _2^2 =Sq_{4,2},\quad \xi _1^3\xi _2 =Sq_{5,1}+Sq_{4,2}, \quad \xi _1^6=Sq_6+Sq_{4,2}. \end{aligned}$$

Again taking $\pi ^*$ on the both sides of the equations, we obtain

$$\begin{aligned} \pi ^*(Sq_{4, 2})&= S_{4, 2} \\ \pi ^*(Sq_{5, 1}+Sq_{4, 2})&= S_{5, 1}+S_{4, 2}+S_{3, 3}+S_{2, 4}+S_{2, 3, 1}+S_{1, 4, 1}\\&\quad + S_{3, 1, 2}+S_{2, 2, 2}+S_{1, 2, 3}+S_{2, 1, 2, 1}+S_{1, 2, 1, 2} \\ \pi ^*(Sq_6+Sq_{4,2})&= S_{6}+S_{4,2}+S_{2,4}. \end{aligned}$$

Finally, by using the upper-triangularity, we obtain

$$\begin{aligned} \pi ^*(Sq_{4,2})&= S_{4,2} \\ \pi ^*(Sq_{5,1})&= S_{5, 1}+S_{3, 3}+S_{2, 4}+S_{2, 3, 1}+S_{1, 4, 1}+S_{3, 1, 2}+S_{2, 2, 2}\\&\quad +S_{1, 2, 3}+S_{2, 1, 2, 1}+S_{1, 2, 1, 2} \\ \pi ^*(Sq_{6})&= S_6+S_{2,4}. \end{aligned}$$

5 Formula for the conjugation

Any connected commutative or co-commutative Hopf algebra has a unique conjugation $\chi$ satisfying

$$\begin{aligned} \chi (1)=1, \quad \chi (xy)=\chi (y)\chi (x), \quad \chi ^2(x)=x, \quad \sum x'\chi (x'')=0, \end{aligned}$$

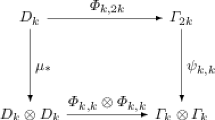
where $\Delta (x)=\sum x'\otimes x''$ and $\deg (x)>0$ [14]. The conjugation invariants in $\mathcal {A}_2^*$ is studied in [5] because it is relevant to the commutativity of ring spectra [1, Lecture 3]. The same problem in $\mathcal {F}_2^*$ has been also studied in [3, 4]. Here we investigate them through our point of view.

Since $\pi ^*$ is a Hopf algebra homomorphism, we have $\pi ^*\circ \chi _{\mathcal {A}_2^*} = \chi _{\mathcal {F}_2^*}\circ \pi ^*$, where $\chi _{\mathcal {A}_2^*}$ and $\chi _{\mathcal {F}_2^*}$ denote the conjugation operations in $\mathcal {A}_2^*$ and $\mathcal {F}_2^*$ respectively. For the module basis $S_I$ in $\mathcal {F}_2^*$, the conjugation $\chi _{\mathcal {F}_2^*}$ is calculated combinatorially.

Definition 2

The coarsening set C(I) of a sequence $I=(i_1,\ldots ,i_l)$ is defined recursively as

$$\begin{aligned} C(I) := \{ (i_1, I'), (i_1+i'_1,I'_2) \mid I'\in C((i_2,\ldots ,i_l))\} \quad \text { and } \quad C((i))=\{ (i) \}, \end{aligned}$$

where $I'_2$ is the tail partial sequence $(i'_2,\ldots ,i'_{l'})$ of $I'=(i'_1,i'_2,\ldots ,i'_{l'})$.

Example 3

$C((a,b,c))=\{ (a,b,c), (a+b,c), (a,b+c), (a+b+c) \}$.

A formula for the conjugation operation in the dual Leibniz–Hopf algebra is given by Ehrenborg [6, Proposition 3.4]. We now give a simple proof for its mod 2 reduction.

Proposition 1

$$\begin{aligned} \chi _{\mathcal {F}_2^*}(S_I)= \sum _{I'\in C(I^{-1})} S_{I'}, \end{aligned}$$

where $I^{-1}=(i_l,\ldots ,i_1)$ is the reverse sequence of $I=(i_1,\ldots ,i_l)$.

Proof

The conjugation is uniquely characterised by

$$\begin{aligned} \chi _{\mathcal {F}_2^*}(1)=1, \quad \sum x'\chi _{\mathcal {F}_2^*}(x'')=0, \end{aligned}$$

where $\Delta (x)=\sum x'\otimes x''$ and $\deg (x)>0$. We put $\chi '(S_I)=\sum _{I'\in C(I^{-1})} S_{I'}$ and show that it satisfies the above equations. It is obvious that $\chi '(1)=1$. Since the co-product is given in (3), the second equation reads

$$\begin{aligned} \sum _{k=0}^{l} S_{i_1,\ldots ,i_k} \chi '(S_{i_{k+1},\ldots ,i_n})=0 \qquad (\forall I=(i_1,i_2,\ldots ,i_n)). \end{aligned}$$

We regard an element of $\mathbb {F}_2\langle \mathcal {W}\rangle$ with a finite subset of $\mathcal {W}$ in the obvious way. We investigate relation between coarsening and the overlapping shuffle product. Define

$$\begin{aligned} C_k(I) =\sum _{ I' \in C((I_{k+1})^{-1})} I' \cdot (i_1, \ldots , i_k). \end{aligned}$$

We observe² that $C(I^{-1}) \subset C_1(I)$ and $C'_1(I):=C_1(I) {\setminus } C(I^{-1})$ consists of those sequences that $i_1$ appears to the left of $i_2$. In turn, $C'_1(I) \subset C_2(I)$ and $C'_2(I):=C_2(I) {\setminus } C'_1(I)$ consists of those sequences that $i_2$ appears to the left of $i_3$. Continuing similarly, we obtain

$$\begin{aligned} C(I^{-1}) =\sum _{k=1}^l C_k(I). \end{aligned}$$

It follows that

$$\begin{aligned} \chi '(S_I)=\sum _{k=1}^l \sum _{I' \in C((I_{k+1})^{-1})} S_{(i_1, \ldots , i_k)}\cdot S_{I'} =\sum _{k=0}^{l} S_{i_1,\ldots ,i_k} \chi '(S_{i_{k+1},\ldots ,i_n})-\chi '(S_{I}) \end{aligned}$$

and $\sum _{k=0}^{l} S_{i_1,\ldots ,i_k} \chi '(S_{i_{k+1},\ldots ,i_n})=0$. $\square$

We give another formula for $\chi _{\mathcal {F}_2^*}(S_I)$.

Definition 3

For a sequence $a_1,a_2,\ldots ,a_n$, the set of ordered block partitions $\mathcal {P}(a_1,a_2,\ldots ,a_n)$ consists of elements of the form

$$\begin{aligned} \beta =((a_1,a_2,\ldots ,a_{i_1}) | (a_{i_1+1},\ldots ,a_{i_2}) | \ldots | (a_{i_{l-1}+1},\ldots ,a_{i_l})), \end{aligned}$$

where $1\le i_1<i_2<\cdots <i_l=n$. We denote $l(\beta )=l$ and $\beta (k)=(a_{i_{k-1}+1},\ldots ,a_{i_k})$. Or inductively, we can define

$$\begin{aligned} \mathcal {P}(a_1,a_2,\ldots ,a_n) = \bigcup _{k=1}^n \bigg \{ ((a_1,\ldots ,a_k)| \beta ) \bigg |\beta \in \mathcal {P}(a_{k+1},a_{k+2},\ldots ,a_n) \bigg \}. \end{aligned}$$

(7)

Theorem 2

$$\begin{aligned} \chi _{\mathcal {F}_2^*}(S_I)=\sum _{\beta \in \mathcal {P}(I)} \prod _{k=1}^{l(\beta )} S_{\beta (k)}. \end{aligned}$$

Proof

Let $I=(a_1,a_2,\ldots ,a_n)$. Put

$$\begin{aligned} \chi '(S_{a_1,a_2,\ldots ,a_n})= \sum _{\beta \in \mathcal {P}(a_1,a_2,\ldots ,a_n)} \prod _{k=1}^{l(\beta )} S_{\beta (k)} \end{aligned}$$

and we check that

$$\begin{aligned} \chi '(1)=1,\quad \sum _{k=0}^{n} S_{a_1,\ldots ,a_k} \chi '(S_{a_{k+1},\ldots ,a_n})=0. \end{aligned}$$

Then, by the uniqueness of the conjugation, we have $\chi _{\mathcal {F}_2^*}=\chi '$. The first assertion is trivial. For the second, observe that by (7)

$$\begin{aligned} \chi '(S_{a_1,a_2,\ldots ,a_n})= & {} \sum _{k=1}^n S_{a_1,\ldots ,a_k} \left( \sum _{\beta \in \mathcal {P}(a_{k+1},a_{k+2},\ldots ,a_n)} \prod _{j=1}^{l(\beta )} S_{\beta (j)} \right) \\= & {} \sum _{k=1}^n S_{a_1,\ldots ,a_k} \chi '(S_{a_{k+1},\ldots ,a_n}). \end{aligned}$$

Hence, we have

$$\begin{aligned} \sum _{k=0}^{n} S_{a_1,\ldots ,a_k} \chi '(S_{a_{k+1},\ldots ,a_n})&= \chi '(S_{a_1,a_2,\ldots ,a_n})+\sum _{k=1}^{n} S_{a_1,\ldots ,a_k} \chi '(S_{a_{k+1},\ldots ,a_n}) \\&= 2\chi '(S_{a_1,a_2,\ldots ,a_n}) \\&=0. \end{aligned}$$

$\square$

Example 4

$$\begin{aligned} \chi _{\mathcal {F}_2^*}(S_{1,2,3})&= S_{3,2,1}+S_{5,1}+S_{3,3}+S_{6} \\&= S_{1,2,3}+S_1 S_{2,3} +S_{1,2}S_3 + S_1 S_2 S_3. \end{aligned}$$

The first line is computed by Proposition 1, and the second by Theorem 2.

Theorem 2 can be thought of as a generalisation of Milnor’s conjugation formula in $\mathcal {A}_2^*$. To see this, we first show a small lemma:

Lemma 4

$$\begin{aligned} \bar{\xi }_n^{2^m}=(S_{2^{n-1}, 2^{n-2}, \ldots , 2^0})^{2^m}=S_{2^{n+m-1}, 2^{n+m-2}, \ldots , 2^m}. \end{aligned}$$

Proof

This is a direct consequence of Corollary 1 combined with Lemma 2. $\square$

Corollary 3

[13, Lemma 10]

$$\begin{aligned} \chi _{\mathcal {A}_2^*}(\xi _n)= \sum _\alpha \prod _{k=1}^{l(\alpha )} \xi _{\alpha (k)}^{2^{\sigma (k)}}, \end{aligned}$$

(8)

where $\alpha =(\alpha (1)|\alpha (2)|\ldots |\alpha (l(\alpha ))$ runs through all the compositions of the integer n and $\sigma (k)=\sum _{j=1}^{k-1} \alpha (j)$.

Proof

We apply the injection $\pi ^*$ to the both sides of (8) and show that they coincide. For the left-hand side, by Lemma 4 we have

$$\begin{aligned} \pi ^*(\chi _{\mathcal {A}_2^*}(\xi _n))=\chi _{\mathcal {F}_2^*}(\pi ^*(\xi _n))= \chi _{\mathcal {F}_2^*}(S_{2^{n-1},2^{n-2},\ldots ,2^0}). \end{aligned}$$

Since $\pi ^*(\xi _{\alpha (k)}^{2^{\sigma (k)}})=S_{2^{\alpha (k)+\sigma (k)-1},\ldots ,2^{\sigma (k)}}$ by Lemma 4, we see

$$\begin{aligned} \pi ^* \left( \prod _{k=1}^{l(\alpha )} \xi _{\alpha (k)}^{2^{\sigma (k)}} \right) = S_{2^{n-1},\ldots ,2^{n-\alpha (l(\alpha ))}} \cdot S_{2^{n-1-\alpha (l(\alpha ))},\ldots ,2^{n-\alpha (l(\alpha ))-\alpha (l(\alpha )-1)}} \cdots S_{2^{\alpha (1)-1},\ldots ,2^0}. \end{aligned}$$

So when $\alpha$ ranges over all compositions of n, we get all the ordered block partitions of the sequence $2^{n-1},2^{n-2},\ldots ,2^0$. The assertion follows from Theorem 2. $\square$

6 Duality between $\mathcal {F}_2$ and $\mathcal {F}_2^*$

In the previous section we discussed how to compute the conjugation in $\mathcal {F}_2^*$. Here, we relate the conjugation in $\mathcal {F}_2$ with that in $\mathcal {F}_2^*$ by using a self-duality of $\mathcal {W}$. Denote $I \preceq I'$ if $I\in C(I')$. We think of $I\in \mathcal {W}$ as a string of 1’s separated by ‘$+$’ and commas; $(\underbrace{1+1+\cdots +1}_{i_1}, \underbrace{1+1+\cdots +1}_{i_2},\ldots ,\underbrace{1+1+\cdots +1}_{i_l})$.

Definition 4

We define the dual $\bar{I}\in \mathcal {W}$ of I by switching $+$ and the commas.

Example 5

For $I=(1,3,2)=(1,1+1+1,1+1)$, its dual is

$$\begin{aligned} \bar{I}=(1+1,1,1+1,1)=(2,1,2,1). \end{aligned}$$

It is easily seen that $\bar{\bar{I}}=I$ and $I \preceq I' \Leftrightarrow \bar{I} \succeq \bar{I}'$. Extend the duality to one between $\mathcal {F}_2$ and $\mathcal {F}_2^*$ by

$$\begin{aligned} D(S^I) = S_{\bar{I}}, \quad D^{-1}(S_I) = S^{\bar{I}}. \end{aligned}$$

Theorem 3

We have $D\circ \chi _{\mathcal {F}_2}= \chi _{\mathcal {F}_2^*}\circ D$. In particular, $f \in \mathcal {F}_2$ is a conjugation invariant if and only if so is $\bar{f} \in \mathcal {F}_2^*$.

Proof

We compute

$$\begin{aligned} D^{-1}\circ \chi _{\mathcal {F}_2^*}\circ D ( S^I )&= D^{-1} \chi _{\mathcal {F}_2^*}(S_{\bar{I}}) = D^{-1} \left( \sum _{I' \preceq (\bar{I})^{-1}} S_{I'}\right) = D^{-1} \left( \sum _{\bar{I}' \succeq I^{-1}} S_{I'}\right) \\&= \sum _{\bar{I}'\succeq I^{-1}} S^{\bar{I}'} = \sum _{I'\succeq I^{-1}} S^{I'}. \end{aligned}$$

Put $\chi '(S^I)=\sum _{I'\succeq I^{-1}} S^{I'}$. Then, one can check $\chi '(1)=1$ and $\sum x' \chi '(x'')=0$ for $\Delta x= \sum x'\otimes x''$ as in Proposition 1. Hence, by the uniqueness of the conjugation, we have $\chi '=\chi _{\mathcal {F}_2}$. $\square$

Example 6

$f=S^{1,1,2}+S^{2,1,1}+S^{1,1,1,1}$ is a $\chi _{\mathcal {F}_2}$-invariant, whilst $D(f)=S_{3,1}+S_{1,3}+S_4$ is a $\chi _{\mathcal {F}_2^*}$-invariant.

Remark 1

The sub-module of the conjugation invariants in $\mathcal {F}_2$ is $\ker (\chi _{\mathcal {F}_2}-1)$ and that in $\mathcal {F}_2^*$ is $\ker (\chi _{\mathcal {F}_2^*}-1)$. The conjugations in $\mathcal {F}_2$ and $\mathcal {F}_2^*$ are dual to each other, and hence, the linear map $\chi _{\mathcal {F}_2}-1$ is transpose to $\chi _{\mathcal {F}_2^*}-1$ with the kernel of same dimension [3]. Theorem 3 gives more information by specifying an explicit correspondence between their elements.